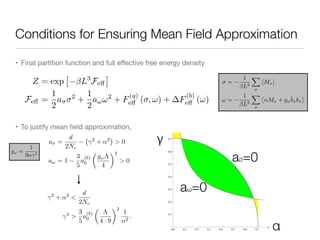
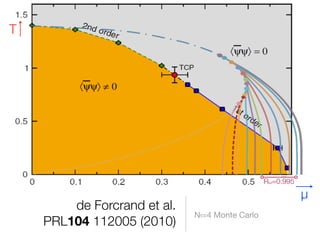
This document summarizes the derivation of an effective free energy for QCD at strong coupling using a mean field approximation with 1 flavor staggered fermion. Key steps include: 1) Performing a path integral over spatial link variables to obtain quark propagators. 2) Introducing auxiliary bosonic fields using a Hubbard-Stratonovich transformation to obtain a bilinear form in quark fields. 3) Applying a mean field approximation to the auxiliary fields. 4) Exactly integrating over temporal links, quark and auxiliary baryon fields to obtain an effective free energy in terms of the auxiliary meson field. 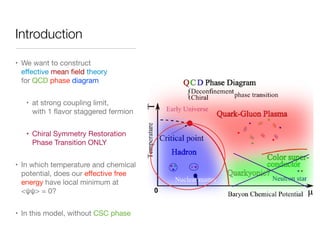5) Analyzing the effective free energy to determine the QCD phase diagram as functions of temperature and

1. Phase diagram at finite T & μ
in strong coupling limit of
lattice QCD
Supervisor: Kazuyuki Kanaya(金谷 和至)
201020283 Jae Don Choi(崔 在敦)

2. Spontaneously Broken QCD Chiral Symmetry
• the fermion part of QCD action (ordinary, continuum theory)
• If massless(m=0), there exists symmetry.
• This means that the action is invariant in
• In sufficiently low temperature, . Symmetry is broken spontaneously.
• Finite temperature QCD.
SF
⇥
, ¯, A
⇤
=
Nf
X
f=1
Z
d4
x ¯(f)
(x)
⇣
µ (@µ + igAµ (x)) + m(f)
⌘
(f)
(x)
=
Nf
X
f=1
Z
d4
x ¯(f)
(x)↵,c
⇣
( µ)↵ ( cd@µ + igAµ (x)cd) + m(f)
↵ cd
⌘
(f)
(x) ,d
SU(Nf )L ⇥ SU(Nf )R
! ei✓ 5

3. Introduction
• We want to construct
effective mean field theory
for QCD phase diagram
• at strong coupling limit,
with 1 flavor staggered fermion
• Chiral Symmetry Restoration
Phase Transition ONLY
• In which temperature and chemical
potential, does our effective free
energy have local minimum at
<ψψ> = 0?
• In this model, without CSC phase

4. On the Starting Line: Lattice QCD
• 1 flavor staggered fermion (4 flavor in continuum limit), color SU(3)
• Detail of action
Z =
Z
D [U0, Uj, , ¯] exp
"
S
(⌧)
F S
(s)
F
X
x
m0 ¯a
x
a
x SG
#
S
(⌧)
F =
1
2
X
x
h
eµ
¯xU0,x x+ˆ0 e µ
¯x+ˆ0U†
0,x x
i
S
(s)
F =
1
2
X
x,j
⌘j,x
h
¯xUj,x x+ˆj ¯x+ˆjU†
j,x x
i
⌘j,x = ( 1)
x0+x1+···xj 1
(j = 1, 2, 3) .
SG =
2Nc
g2

1
trc
2Nc
⇥
Uµ⌫,x + U†
µ⌫,x
⇤
! 0 g2
! 1
Strong coupling limit

5. Process
• Start with partition function.
• Path integral of spatial link variable
• Bosonization: to make bilinear form in quark for path integral of
• Mean field approximation in auxiliary fields
• Execute integral of quark & temporal link variable
• acquisition of effective free energy
• Analyze in temperature and chemical potential
Uj,x
U0,x
¯,
¯,

6. Introduction
• Analytical approach (Kawamoto et al. ’07)
• 1 flavor staggered fermion (4 flavor in continuum limit), color SU(3)
• Detail of action
Z =
Z
D [U0, Uj, , ¯] exp
"
S
(⌧)
F S
(s)
F
X
x
m0 ¯a
x
a
x SG
#
Strong coupling limit
a⌧ = as = 1
S
(⌧)
F = a3
sa⌧
X
x
"
eµa⌧
¯xU0,x x+ˆ0 e µa⌧
¯x+ˆ0U†
0,x x
2a⌧
#
S
(s)
F = a3
sa⌧
X
x,j
⌘j,x
"
¯xUj,x x+ˆj ¯x+ˆjU†
j,x x
2as
#
⌘j,x = ( 1)
x0+x1+···xj 1
(j = 1, 2, 3) .
SG =
2Nc
g2

1
trc
2Nc
⇥
Uµ⌫,x + U†
µ⌫,x
⇤
! 0 g2
! 1

7. SU(3) Group Integral with Spatial Link Variable
• Kluberg-Stern et al. (’83)
Mx = ¯a
x
a
x
Bx =
1
Nc!
"a1a2···aNc a1 a2
· · · aNc
¯Bx =
1
Nc!
"a1a2···aNc
¯aNc
· · · ¯a2
¯a1
Z
D [Uj] e S
(s)
F =
Z
D [Uj] exp
2
4 1
2
·
X
x,j
⌘j,x
⇣
¯xUj,x x+ˆj ¯x+ˆjU†
j,x x
⌘
3
5
= exp
2
4
X
x
1
4Nc
dX
j=1
MxMx+ˆj
X
x
( 1)
Nc(Nc 1)
2
dX
j=1
⇣⌘j,x
2
⌘Nc
h
¯BxBx+ˆj + ( 1)
Nc ¯Bx+ˆjBx
i
X
x
N2
c · (Nc 2)! Nc!
32 · N2
c · Nc!
dX
j=1
M2
xM2
x+ˆj
X
x
2 · Nc! N3
c · (Nc 2)!
128 · N4
c · Nc!
dX
j=1
M3
xM3
x+ˆj
3
5

8. Systematic 1/d Expansion I
• At d (space dimension) →∞, mean field theory becomes exact.
• demand the leading order term be O(1) at d→∞ : Rescale quark field
x ! d
1
4
x
Mx =
p
d · [¯a
x
a
x]
Bx = d
Nc
4 ·

1
Nc!
"a1a2···aNc a1 a2
· · · aNc
¯Bx = d
Nc
4 ·

1
Nc!
"a1a2···aNc
¯aNc
· · · ¯a2
¯a1

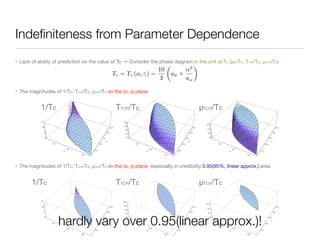
9. Systematic 1/d Expansion II
• Then our result looks like
• Kluberg-Stern et al. (’83) : Contribution of higher order terms to Vacuum Expectation Value of chiral
condensate(<ψψ>) is small at zero temperature(T=0). (In d=4, about 7%)
• Usually, Analyzed only in O(1): Damgaard et al.(’84), Nishida(’04), Miura et al.(’07), Nakano et al.(’10),... etc.
• We want to investigate the baryon effect: We adopt not only O(1) but also O(1/√d) for our effective action.
Z
D [Uj] e S
(s)
F = exp
2
4
X
x
1
d
dX
j=1
⇢
1 ·
✓
1
4Nc
· MxMx+ˆj
◆
+
1
p
dNc 2
·
✓
( 1)
Nc(Nc 1)
2
⇣⌘j,x
2
⌘Nc
·
⇣
¯BxBx+ˆj + ( 1)
Nc ¯Bx+ˆjBx
⌘◆
+
1
d
·
✓
N2
c · (Nc 2)! Nc!
32 · N2
c · Nc!
· M2
xM2
x+ˆj
◆
+
1
d2
·
✓
2 · Nc! N3
c · (Nc 2)!
128 · N4
c · Nc!
· M3
xM3
x+ˆj
◆
O(1)
O(1/√d) @ Nc=3
O(1/d)
O(1/d^2)

10. After the Path Integral of Spatial Link Variable
• So far, our partition function
• Propagators and inner product
VM,xy =
1
2d
dX
j=1
⇣
y,x+ˆj + y,x ˆj
⌘
VB,xy = ( 1)
Nc(Nc 1)
2
dX
j=1
⇣⌘j,x
2
⌘Nc
⇣
y,x+ˆj + ( 1)
Nc
y,x ˆj
⌘
(A, V B) =
X
x,y
AxVxyBy
Z =
Z
D [U0, Uj, , ¯] exp
"
S
(⌧)
F
X
x
m0 ¯a
x
a
x S
(s)
F
#
⇡
Z
D [U0, , ¯] exp
"
S
(⌧)
F
X
x
m0Mx +
d
2Nc
·
1
2
(M, VM M) + ¯B, VBB
#

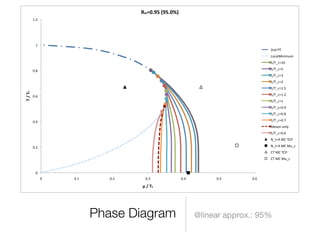
11. Bosonization: Introducing Auxiliary Fields
• We want the bilinear form of quark → Hubbard-Stratonovich transformation
Da;x =
2
"abc
b
x
c
x +
1
3
¯a
xbx
D†
a;x =
2
"abc ¯c
x ¯b
x +
1
3
¯bx
a
x
d
2Nc
·
1
2
(M, VM M)
2
2
(M, M)
↵2
2
(M, M) =
1
2
⇣
M, eVM M
⌘
¯b, V 1
B b g!! ¯b, b =
⇣
¯b, eV 1
B b
⌘
e( ¯B,VBB) = det VB
Z
D
⇥
¯b, b
⇤
e (¯b,V 1
B b)+(¯b,B)+( ¯B,b)
e( ¯B,b)+(¯b,B) =
Z
d
⇥
a, †
a
⇤
exp
"
†
a, a +
X
x
†
a;xDa;x + D†
a;x a;x
2
2
(M, M) +
X
x
1
9 2
Mx
¯bxbx
#
e
P
x
1
9 2 Mx
¯bxbx
=
Z
D [!] exp
"
1
2
(!, !) ↵
X
x
Mx + g!
¯bxbx !x
↵2
2
(M, M)
#
e
1
2 (M,eVM M) =
Z
D [ ] exp

1
2
⇣
, eVM
⌘ ⇣
, eVM M
⌘
Z =
Z
D [U0, , ¯] exp
"
S
(⌧)
F +
d
2Nc
·
1
2
(M, VM M) + ¯B, VBB
X
x
m0Mx
#
g! =
1
9↵ 2
free parameters α, γ

12. Mean Field Approximation
• Bosonic auxiliary fields (Not baryon auxiliary fields!!!)
• After the approximation,
• parameter dependence in α, γ : later, indefiniteness of this model...
Z =
Z
D
⇥
U0, , ¯,¯b, b
⇤
⇥ det VB ⇥ exp

S
(q)
F
⇣
¯b, eV 1
B b
⌘
L3
✓
†
a a +
1
2
!2
+
a
2
2
◆
S
(q)
F = S
(⌧)
F +
X
x
(a + ↵! + m0) Mx
+
1
3
⇥ †
a (¯a
, b) + a
¯b, a
⇤
+
2
"cab
⇥ †
c
a
, b
+ c ¯b
, ¯a
⇤
=
1
L3
X
x
hMxi
! =
1
L3
X
x
⌦
↵Mx + g!
¯bxbx
↵
a =
1
L3
X
x
⌧
2
"abc
b
x
c
x +
1
3
¯a
xbx
a =
d
2Nc
2
+ ↵2

13. Effective Free Energy
• At φ=0: Analysis too complicated with nonzero diquark condensate
• without color superconductor phase in this approximation
• Exact integration over , and (gauge fixing with Polyakov gauge)
• Integration over with spherical integrate approximation
• Acquiring the effective free energy!
Z = exp
⇥
L3
Fe↵
⇤
= exp

L3
✓
F
(b)
e↵ + F
(q)
e↵ +
1
2
!2
+
a
2
2
◆
Fe↵ =
1
2
a 2
+
1
2
"
1
3
5
a
(b)
0
✓
g!⇤
4
◆2
#
!2
+ F
(b)
e↵ (!) + F
(q)
e↵
=
1
2
a 2
+
1
2
a!!2
+ F
(q)
e↵ ( , !) + F
(b)
e↵ (!)

14. Effective Free energy II
• Final result of effective free energy
Z = exp
⇥
L3
Fe↵
⇤
= exp

L3
✓
F
(b)
e↵ + F
(q)
e↵ +
1
2
!2
+
a
2
2
◆
Fe↵ =
1
2
a 2
+
1
2
"
1
3
5
a
(b)
0
✓
g!⇤
4
◆2
#
!2
+ F
(b)
e↵ (!) + F
(q)
e↵
=
1
2
a 2
+
1
2
a!!2
+ F
(q)
e↵ ( , !) + F
(b)
e↵ (!)
F
(q)
e↵ ( , !) = T log
"
4
3
✓
cosh
Eq ( , !)
T
◆3
2
3
cosh
Eq ( , !)
T
+
1
3
cosh
Ncµ
T
#
F
(b)
e↵ (!) =
1
2
·
"
3
5
a
(b)
0
✓
g!⇤
4
◆2
#
!2
+
3
28
a
(b)
0
✓
g!⇤
4
◆4
!4
+ O !6
| {z }
= F
(b)
eff (!)

15. Conditions for Ensuring Mean Field Approximation
• Final partition function and full effective free energy density
• To justify mean field approximation,
=
1
L3
X
x
hMxi
! =
1
L3
X
x
⌦
↵Mx + g!
¯bxbx
↵
a =
d
2Nc
2
+ ↵2
> 0
a! = 1
3
5
a
(b)
0
✓
g!⇤
4
◆2
> 0
2
+ ↵2
<
d
2Nc
4
>
3
5
a
(b)
0
✓
⇤
4 · 9
◆2
1
↵2
.
Z = exp
⇥
L3
Fe↵
⇤
Fe↵ =
1
2
a 2
+
1
2
a!!2
+ F
(q)
e↵ ( , !) + F
(b)
e↵ (!)
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7
a
0.1
0.2
0.3
0.4
0.5
0.6
0.7
g! =
1
9↵ 2
α
γ
aσ=0
aω=0

16. Equilibrium Condition
• Discussion is complicated with two
order parameters, σ, ω.
• If ΔFeff,(b)=O(ω^4) is ignorable,
• Suggestion for evaluation criteria
• With this, only one order parameter, σ !
@Fe↵
@
= a + a
@F
(q)
e↵
@mq
= 0
@Fe↵
@!
= a!! +
@ F
(b)
e↵
@!
+ ↵
@F
(q)
e↵
@mq
= 0
50%
95%
99%
99.5%
99.7%
⇡
a!
↵
!
α
γ
1
2 a!!2
F
(b)
e↵
1
2 a!!2
!=1
= 0.95 or 0.99, ...

17. Effective Free energy as a Function of σ
• (α, γ) = (0.2, 0.678233) : Kawamoto et al. (’07)
Feff / Tc
σ
Feff / Tc
σ
Feff / Tc
σ
2nd order phase transition
from T=0 (fixed at μ=0)
1st order phase transition
from μ=0 (fixed at T=0)
Around Tricritical point
from μ=0 (fixed at T=TTCP)

18. Indefiniteness from Parameter Dependence
• Lack of ability of prediction on the value of Tc → Consider the phase diagram in the unit of Tc (μc/Tc, TTCP/Tc, μTCP/Tc)
• The magnitudes of 1/Tc, TTCP/Tc, μTCP/Tc on the (α, γ) plane
• The magnitudes of 1/Tc, TTCP/Tc, μTCP/Tc on the (α, γ) plane, especially in credibility 0.95(95%, linear approx.) area.
Tc = Tc (↵, ) =
10
3
✓
a +
↵2
a!
◆
1/Tc TTCP/Tc μTCP/Tc
1/Tc TTCP/Tc μTCP/Tc
0.2
0.4
0.6
a 0.3
0.4
0.5
0.6
0.7
g
0
5
10
15
0.2
0.4
0.6
a 0.3
0.4
0.5
0.6
0.7
g
0.0
0.2
0.4
0.6
0.8
0.2
0.4
0.6
a 0.3
0.4
0.5
0.6
0.7
g
0.0
0.1
0.2
0.3

19. Indefiniteness from Parameter Dependence
• Lack of ability of prediction on the value of Tc → Consider the phase diagram in the unit of Tc (μc/Tc, TTCP/Tc, μTCP/Tc)
• The magnitudes of 1/Tc, TTCP/Tc, μTCP/Tc on the (α, γ) plane
• The magnitudes of 1/Tc, TTCP/Tc, μTCP/Tc on the (α, γ) plane, especially in credibility 0.95(95%, linear approx.) area.
Tc = Tc (↵, ) =
10
3
✓
a +
↵2
a!
◆
1/Tc TTCP/Tc μTCP/Tc
1/Tc TTCP/Tc μTCP/Tc
0.2
0.4
0.6
a 0.3
0.4
0.5
0.6
0.7
g
0
5
10
15
0.2
0.4
0.6
a 0.3
0.4
0.5
0.6
0.7
g
0.0
0.2
0.4
0.6
0.8
0.2
0.4
0.6
a 0.3
0.4
0.5
0.6
0.7
g
0.0
0.1
0.2
0.3
hardly vary over 0.95(linear approx.)!

20. Phase Diagram @linear approx.: 95%
0"
0.2"
0.4"
0.6"
0.8"
1"
1.2"
0" 0.1" 0.2" 0.3" 0.4" 0.5" 0.6"
T"/"Tc"
μ"/"Tc"
Rω=0.95"(95.0%)"
2nd"PT"
LocalMinimum"
1/T_c=10"
1/T_c=5"
1/T_c=3"
1/T_c=2"
1/T_c=1.5"
1/T_c=1.2"
1/T_c=1"
1/T_c=0.9"
1/T_c=0.8"
1/T_c=0.7"
Meson"only"
1/T_c=0.6"
N_t=4"MC"TCP"
N_t=4"MC"Mu_c"
CT"MC"TCP"
CT"MC"Mu_c"

21. de Forcrand et al.
PRL104 112005 (2010)
Nt=4 Monte Carlo
Rω=0.995
μ
T

22. de Forcrand et al.
arXiv:1111.1434 (2011)
Continuous time Monte Carlo
T
μRω=0.995

23. Summary and Future Works
• Analytical approach at strong coupling limit (mean field approximation)
• In spite of the model with meson only(Nishida ’04), this model has indefiniteness.
• Improvement of zero diquark condensate to nonzero.
• Considering diquark → Considering color superconductor phase
• The limitation of mean field analysis...?
• Auxiliary field Monte Carlo simulation: Ohnishi et al. (arXiv:1211.2282v1)
• Missing Link between mean field analysis & Monte Carlo simulation?
• At mean field analysis: Improvement of O(1/g^2), O(1/d) accuracy.

24. ありがとうございました。
Thank you very much.