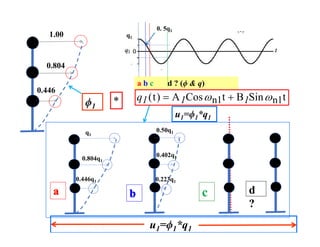
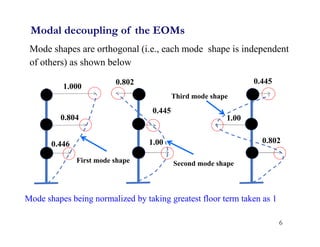
This document discusses modal response spectrum analysis for earthquake engineering. Some key points: - The equations of motion for a multi-degree of freedom structural system can be decoupled into individual single-degree of freedom equations through modal analysis. - Mode shapes are orthogonal and form a modal matrix that transforms displacement coordinates into modal coordinates. This results in uncoupled equations for each vibration mode. 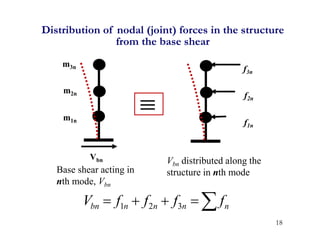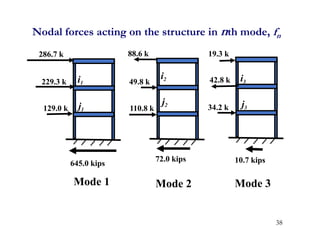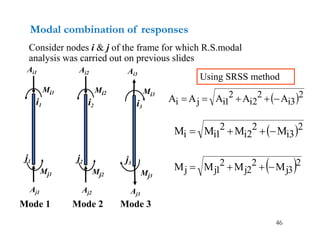- Earthquake excitation is represented as a modal force vector. Response of each mode is then determined independently through its modal mass, stiffness and damping. 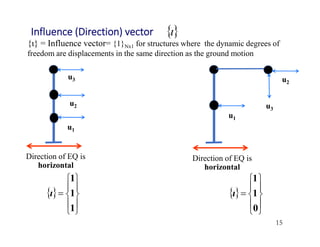- Participation factors relate the modal displacements back to the physical displacements of the structure and determine the effective modal weight contributing to response in each mode.

1. CE-412: Introduction to Structural Dynamics and Earthquake
Engineering
MODULE 9
1
University of Engineering & Technology,
Peshawar, Pakistan
MODAL RESPONSE SPECTRUM ANALYSIS

2. 2
Modal decoupling of the EOMs
It is already known that the equations of motion for a a MDOF with
lumped mass system and undergoing only lateral displacement can
be written as:
          
p(t)
u
k
u
c
u
m 

 



3. 3
Let be the modal matrix (matrix of mode shapes) in which the
nth column is the nth mode shape of vibration (i.e. each column
represents a particular mode shape).
Recalling the results of Prob M8.2
 

Modal decoupling of the EOMs
 




























445
.
0
802
.
0
000
.
1
000
.
1
445
.
0
804
.
0
802
.
0
000
.
1
446
.
0
3
2
1
0.555
0.802
2.243
1.247
0.445
1.802
1.000
1.00
1.000



    
q
u 

    
q
u 
 

    
q
u 


 

Where {u} is displacement vector and {q} is
the modal amplitude vector (i.e. matrix of
displacement amplitude)

4. t
Sin
B
t
Cos
A
)
t
( 1
n
1
n 
 1
1
1
q 

0.446
0.804
1.00
*
0. 5q1
q1
a b c d ? (ϕ & q)
ϕ1
q1
0.804q1
0.446q1
0.50q1
0.402q1
0.223q1
c d
?
u1=ϕ1*q1
u1=ϕ1*q1

5. 5
Substituting values of from slide 3 in the:
             
p(t)
q
k
q
c
q
m 




 


Modal decoupling of the EOMs
          
p(t)
u
k
u
c
u
m 

 


     
u
u
u 

 &
,
 T

                     
p(t)
q
k
q
c
q
m
T
T
T
T









 


          
P(t)
q
K
q
C
q
M 

 


Pre-multiply both sides by
Where = Modal mass matrix
= Modal stiffness matrix
= Modal damping matrix
= Modal (applied) forces vector
 
M
 
C
 
K
 
)
t
(
P

6. 6
Modal decoupling of the EOMs
Mode shapes are orthogonal (i.e., each mode shape is independent
of others) as shown below
0.445
0.802
1.00
1.00
0.445
0.802
0.446
0.804
1.000
First mode shape Second mode shape
Third mode shape
Mode shapes being normalized by taking greatest floor term taken as 1

7. 7
Modal decoupling of the EOMs
A matrix said to be orthogonal if where [I] is
an identity matrix in which diagonal terms are 1 and off diagonal
terms are 0 and therefore det [I]=1. are diagonal
matrices (i.e., matrices in which off diagonal terms are zero)
 
A      
I
A
A
T

     
C
and
K
,
M
m1
m2
m3
k1
k2
k3
 











3
2
1
m
0
0
0
m
0
0
0
m
m
m3
m2
m1

8. 8
Modal decoupling of the EOMs
Since are diagonal matrices so the N
coupled equations replaces by N uncoupled equation for SDOF
systems
     
K
and
C
,
M
(t)
P
q
K
q
C
q
M n
n
n
n
n
n
n


 


Where Mn= Generalized mass for the nth natural mode
Kn= Generalized stiffnes for the nth natural mode
Cn= Generalized damping for the nth natural mode
Pn(t)= Generalized force for the nth natural mode

9. 9
Modal decoupling of the EOMs
The equation given on previous slide is for nth mode of MDOF of
order N. All the independent equations for N modes in matrix form
can be written as
Where M= Diagonal matrix of the generalized modal masses
K= Diagonal matrix of the generalized modal stiffnesses
C= Diagonal matrix of the generalized modal dampings
P(t) = Column vector of the generalized modal forces Pn(t)
(t)
P
Kq
q
C
q
M 

 



10. 10
Modal analysis for earthquake forces
The uncoupled equations of motions for earthquake excitations can
be written as
{ι}= Influence vector (refer slide 15 for details) of size Nx1.
{ι} = {1}Nx1 for structures where the dynamic degrees of freedom
are displacements in the same direction as the ground motion
              
)
(t
p
(t)
P
q
K
q
C
q
M eff
T
eff 



 


    )
(t
u
m
(t)
p
Where g
eff





               )
t
(
u
m
q
q
q g
T 



 






 (t)
P
K
C
M eff

11. 11
Modal analysis for earthquake forces
Replacing
For nth mode
     
L
m
T

 
             )
(t
u
L
(t)
P
q
K
q
C
q
M g
eff




 





)
(t
u
L
q
K
q
C
q
M g
n
n
n
n
n
n
n




 



)
(t
u
M
L
q
M
K
q
M
M
2
q
M
M
g
n
n
n
n
n
n
n
n
n
n
n
n
n




 





)
(
2
t
u
M
L
q
q
2
q
or g
n
n
n
n
n
n
n
n




 


 


L and m has
same units

12. 12
Modal Participation factors
The term Ln/Mn has been given the name of participation factor for
the nth mode and is represented by Γn (capital Greek alphabet for
Gamma)
Γn is usually considered a measure of the degree to which the nth
mode participates in the response. This terminology is misleading,
however, because Γn is not independent of how the mode is
normalized, nor a measure of the modal contribution to a response
quantity.
The magnitude of the participation factor is dependent on the
normalization method used for the mode shapes.
   
    
n
T
n
T
n
n
n
n
m
m
M
L








13. 13
Participation factors
Once the modal amplitudes {q} have been found the
displacements of the structure are obtained from
The above mentioned equation to determine modal displacements
cancel out the effect of normalization carried out to calculate q
(slide 11).
The displacements associated with the nth mode are given by
    
q
u 

    
(t)
q
(t)
u n
n
n 


14. 14
Effective weight of structure in nth mode, Wn
Effective weight of structure in nth mode=
It shall be noted that the sum of the all effective weights for an
excitation in a given direction ( i.e. for a given {ι}) should equal
the total weight of the structure. Note, this may not be the case
where rotational inertia terms also exist in the mass matrix.
Many building codes require that a sufficient number of modes
be used in the analyses such that the sum of the effective weights is
at least 90% of the weight of the structure. This provides a measure
on the number of modes required in the analysis.
      
    
  g
M
L
)
g
L
(
g
L
M
L
g
m
m
W
n
2
n
n
n
n
n
n
n
T
n
T
n
T
n
n 










m

15. 15












1
1
1
ι
Influence (Direction) vector 

{ι} = Influence vector= {1}Nx1 for structures where the dynamic degrees of
freedom are displacements in the same direction as the ground motion
Direction of EQ is
horizontal
u1
u2
u3
Direction of EQ is
horizontal
u1
u2
u3












0
1
1
ι

16. 16
Base Shear Force in the structure in the nth node, Vbn
The base shear in nth mode can be determined using relation
Where Wn = Effective weight of structures in nth mode


















g
A
g
M
L
g
A
W
V
n
2
n
n
bn
n
n

17. 17
Distribution of nodal (joint) forces in the structure
from the base shear
In many design codes the first step is to compute the modal base
shear force and this is then distributed along the structures (shown
on next slide) to each degrees of freedom.
The distributed loads are assumed to give the same displacements
in the structure as those generated by the exciting base shear.
    
n
n
bn
n m
L
V
f 


18. 18

Base shear acting in
nth mode, Vbn
Vbn distributed along the
structure in nth mode




 n
n
n
n
bn f
f
f
f
V 3
2
1
Distribution of nodal (joint) forces in the structure
from the base shear
Vbn
m1n
m2n
m3n
f1n
f2n
f3n

19. 19
Response spectrum model analysis: Example
A 3 story R.C. building as shown below is required to be
designed for a design earthquake with PGA=0.3g, and its elastic
design spectrum is given by Fig 6.9.5 multiplied by 0.3). Carry
out the dynamic analysis by using the above mentioned design
spectrum. Take:
 Story height = 10ft
Total stiffness of each story = 250 kips/in.
 Weight of each floor = 386.4 kips
m1
m2
m3
k1
k2
k3

20. 20
Mass and stiffness matrices
 











1
0
0
0
1
0
0
0
1
m
m=W/g = (386.4k) /(386.4 in/sec2)= 1.0 kip-sec2/in
 















250
250
0
250
500
250
0
250
500
k
   



















2
2
2
2
250
250
0
250
500
250
0
250
500
n
n
n
n m
k





21. 21
   
  0
det
2

 m
k
Setting n
 yields following values
sec
/
49
.
28
sec
/
69
.
19
sec
/
04
.
7
3
2
1
rad
rad
rad
n
n
n






sec
22
.
0
sec
32
.
0
sec
89
.
0
3
2
1



n
n
n
T
T
T
Natural frequencies

22. 22
0
250
250
0
250
500
250
0
250
500
31
21
11
2
1
2
1
2
1



































n
n
n
Normalized coordinates of first mode shape
   
   0
1
2
1 
 
 m
k n
Substituting 1
and
56
.
9
4 11
2
1

 
n
Mode shapes

23. 23
0
1
44
.
200
250
0
250
44
.
450
250
0
250
44
.
450
31
21




























First row gives 80
.
1
0
250
44
.
450 21
21 


 

24
.
2
0
250
)
80
.
1
(
44
.
450
250
0
250
44
.
450
250
31
31
31
21















Second row gives
 
















































1.00
0.80
0.45
2.24/2.24
1.80/2.24
1.00/2.24
31
21
11
1
2.24
1.80
1.00




Mode shapes

24. 24
0
7
.
387
250
250
0
250
7
.
387
500
250
0
250
7
.
387
500
32
22
12
































7
.
387
2
2

n

0
1
3
.
137
250
0
250
3
.
112
250
0
250
3
.
112
32
22





























80
.
0
&
45
.
0
32
22






























0.80
0.45
1.00
32
22
12



Mode shapes

25. 25






































0.45
1.00
0.80
Similarly
33
23
31
0.56
1.25
1.00



 




































0.45
1.00
0.80
0.80
0.45
1.00
1.00
0.80
0.45
3
2
1
0.56
1.25
1.00
0.80
0.45
1.00
2.24
1.80
1.00



Mode shapes

26. 26
Modal mass, Mn and participation factor,Γn
   
    
n
T
n
T
n
n
n
n
m
m
M
L







   
    
1
1
1
1
1
1



m
m
M
L
T
T
1



For structure given in problem{ι}={1}
   
    
n
T
n
T
n
n
n
n
m
m
M
L


 1





27. 27































1
1
1
1
0
0
0
1
0
0
0
1
00
.
1
80
.
0
45
.
0
T
1
L











1
1
1
1.00
0.80
.45
0
1
L
/ft
sec
-
kip
7
2
/in.
sec
-
kip
25
.
2
L 2
2 

1
   
































1
1
1
1
0
0
0
1
0
0
0
1
1
31
21
11
1
T
T
1 m
L




Modal mass, Mn and participation factor,Γn

28. 28
    
1
1
1 
 m
M
T
































00
.
1
80
.
0
45
.
0
1
0
0
0
1
0
0
0
1
00
.
1
80
.
0
45
.
0
T
1
M











00
.
1
80
.
0
45
.
0
1.00
0.80
.45
0
1
M
/ft
sec
-
kip
22.1
/in.
sec
-
kip
84
.
1 2
2


1
M
Modal mass, Mn and participation factor,Γn

29. 29
22
.
1
84
.
1
25
.
2
1
1 



M
L1
Similarly 36
.
0
84
.
1
65
.
0
2
2 



M
L2
14
.
0
84
.
1
25
.
0
3
3 



M
L3
Participation factor, Γn

30. 30
Effective weight of structure participating in nth mode, Wn
      
    
g
M
L
g
m
m
m
W
n
n
n
T
n
T
n
T
n
n
2








/in
sec
-
kip
4
.
386 2

g
  kips
1
.
1063
4
.
386
*
84
.
1
25
.
2
2
1
2
1
1 

 g
M
L
W
  kips
7
.
88
4
.
386
*
84
.
1
65
.
0
2
2
2
2
2 

 g
M
L
W
  kips
1
.
13
4
.
386
*
84
.
1
25
.
0
2
3
2
3
3 

 g
M
L
W

31. 31
Mass of the structure participating in nth mode , PMn
Participating mass of the structure in nth mode=
W
W
PM n
n 
*
%
7
.
91
917
.
0
4
.
386
*
3
1
.
1063
1
*
1 



W
W
PM
%
7
.
7
077
.
0
4
.
386
*
3
7
.
88
2
*
2 



W
W
PM
%
13
.
1
0113
.
0
4
.
386
*
3
1
.
13
3
*
3 



W
W
PM
00
.
1
PM 


Most of the code requires that such number of modes shall be
considered so that ΣPM≥ 0.9. In our case, indeed, the consideration
of just the first mode would have been sufficient as PM1≥ 0.9

32. 32


















g
W
g
g
M
L
V n
n
n
n
n
bn
A
A
2
Base shear in nth mode, Vbn
Mode 1: Tn1=0.89 sec
kips
g
g
T
g
W
V
n
1
b 0
.
645
3
.
0
*
1
*
8
.
1
*
1
.
1063
.
A
1
1
1 


















kips
g
g
g
W
V 2
b 1
.
72
3
.
0
*
71
.
2
*
7
.
88
3
.
0
*
A
:
sec
0.32
T
For 2
2
n2 











kips
g
g
g
W
V 3
b 7
.
10
3
.
0
*
71
.
2
*
1
.
13
3
.
0
*
A
:
sec
0.22
T
For 3
3
n3 











Values of A for each Tn can be
determined from Fig. 6.9.5 given
on next slide

33. 33
0.22 s
0.32 s
0.89 s
sec
22
.
0
sec
32
.
0
sec
89
.
0
3
2
1



n
n
n
T
T
T

34. 34
Nodal forces acting on the structure in nth mode, fn
    
n
n
bn
n m
L
V
f 

   











































31
21
11
1
1
31
21
11
3
2
1
1
1
3
2
1






m
L
V
f
f
f
m
L
V
f
f
f
b
n
n
n
b
n
n
n
First mode










































7
.
286
3
.
229
0
.
129
00
.
1
80
.
0
45
.
0
12
0
0
0
12
0
0
0
12
)
12
*
25
.
2
(
645
31
21
11
f
f
f

35. 35
    
n
n
bn
n m
L
V
f 

 













































0.80
0.45
1.00
12
0
0
0
12
0
0
0
12
)
12
*
65
.
0
(
1
.
72
32
22
12
2
2
32
22
12



m
L
V
f
f
f
b
Second mode
























6
.
88
8
.
49
8
.
110
32
22
12
f
f
f
Nodal forces acting on the structure in nth mode, fn

36. 36
    
n
n
bn
n m
L
V
f 

 













































0.45
1.00
0.80
12
0
0
0
12
0
0
0
12
)
12
*
25
.
0
(
7
.
10
33
23
13
3
3
33
23
13



m
L
V
f
f
f
b
Third mode
























3
.
19
8
.
42
2
.
34
33
23
13
f
f
f
Nodal forces acting on the structure in nth mode, fn

37. 37
   


















3
.
19
8
.
42
2
.
34
6
.
88
8
.
49
8
.
110
7
.
286
3
.
229
0
.
129
3
2
1 n
n
n
n f
f
f
f
Nodal forces acting on the structure in nth mode, fn

38. 38
645.0 kips
Mode 1
286.7 k
229.3 k
129.0 k
i1
j1
10.7 kips
Mode 3
19.3 k
42.8 k
34.2 k
i3
j3
Mode 2
72.0 kips
88.6 k
49.8 k
110.8 k
i2
j2
Nodal forces acting on the structure in nth mode, fn

39. 39
Combination of Modal Maxima
The use of response spectra techniques for multi-degree of
freedom structures is complicated by the difficulty of combining
the responses of each mode.
It is extremely unlikely that the maximum response of all
the modes would occur at the same instant of time.
When one mode is reaching its peak response there is no way of
knowing what another mode is doing.
The response spectra only provide the peak values of the
response, the sign of the peak response and the time at which the
peak response occurs is not known.

40. 40
Combination of Modal Maxima
Therefore
and, in general
The combinations are usually made using statistical methods.
    max
max q
u 

    max
max q
u 


41. 41
Combined Response ro
Let rn be the modal response quantity (base shear, nodal
displacement, inter-storey drift, member moment, column stress
etc.) for mode n .The r values have been found for all modes (or
for as many modes that are significant).
Most design codes do not require all modes to be used but many do
require that the number of modes used is sufficient so that the sum
of the Effective Weights of the modes reaches, say, 90% of the
weight of the building. Checking the significance of the
Participation Factors may be useful if computing deflections and
rotations only.

42. 42
Absolute sum (ABSSUM) method
The maximum absolute response for any system response quantity
is obtained by assuming that maximum response in each mode
occurs at the same instant of time. Thus the maximum value of the
response quantity is the sum of the maximum absolute value of the
response associated with each mode. Therefore using ABSSUM
method
This upper bound value is too conservative. Therefore, ABSSUM
modal combination rules is not popular is structural design
applications



N
n
no
o r
r
1

43. 43
Square-Root-of-the Sum-of-the-Squares (SRSS) method
The SRSS rule for modal combination, developed in E.Rosenblueth’s
PhD thesis (1951) is
The most common combination method and is generally satisfactory
for 2-dimensional analyses is the square root of the sum of the
squares method. The method shall not be confused with the root-
mean-square of statistical analysis as there is no denominator.
 2
/
1
1
2



N
n
no
o
r
r

44. 44
This method was very commonly used in design codes until about
1980. Most design codes up to that time only considered the
earthquake acting in one horizontal direction at a time and most
dynamic analyses were limited to 2-dimensional analyses.
Square-Root-of-the Sum-of-the-Squares (SRSS) method

45. 45
Three Dimensional Structures
In three-dimensional structures, different modes of free-
vibration in different directions may have very similar natural
frequencies.
If one of these modes is strongly excited by the earthquake at a
given instant of time then the other mode, with a very similar
natural frequency, is also likely to be strongly excited at the same
instant of time. These modes are often in orthogonal horizontal
directions but there may be earthquake excitation directions where
both modes are likely to be excited.
In these cases the Root-Sum-Square or SRSS combination
method has been shown to give non-conservative results for the
likely maximum response. In such cases some other methods such
as CQC, DSC are used

46. 46
Modal combination of responses
Using SRSS method
 2
3
i
2
2
i
2
1
i
j
i A
A
A
A
A 




j3
Aj3
Mj3
i3
Mi3
Ai3
Aj1
j1
Mj1
i1
Mi1
Ai1
Aj2
j2
Mj2
i2
Mi2
Ai2
 2
3
i
2
2
i
2
1
i
i M
M
M
M 



 2
3
j
2
2
j
2
1
j
j M
M
M
M 



Mode 1 Mode 2 Mode 3
Consider nodes i & j of the frame for which R.S.modal
analysis was carried out on previous slides

47. 47
Caution
It must be stressed that what ever response item r that the
analyst or designer requires it must be first computed in each mode
before the modal combination is carried out.
If the longitudinal stress is required in a column in a frame, then
the longitudinal stress which is derived from the axial force and
bending moment in the column must be obtained for each mode
then the desired combination method is used to get the maximum
likely longitudinal stress.
It is NOT correct to compute the maximum likely axial force and
the maximum likely bending moment for the column then use these
axial forces and bending moments, after carrying out their modal
combinations, to compute the longitudinal stress in the column.

48. 48
Home Assignment No. M9
A 3 story R.C. building as shown below is required to be
designed for a design earthquake with PGA=0.25g, and its elastic
design spectrum is given by Fig 6.9.5 (Chopra’s book) multiplied
by 0.25). It is required to carry out the dynamic modal analysis by
using the afore mentioned design spectrum . Take:
• Story height = 10ft
•Total stiffness of first 2 stories = 2000 kips/ft.
• Total stiffness of top floor = 1500 kips/ft
• Mass of first 2 floors = 5000 slugs
• Mass of top floor = 6000 slugs
m1
m2
m3
k1
k2
k3