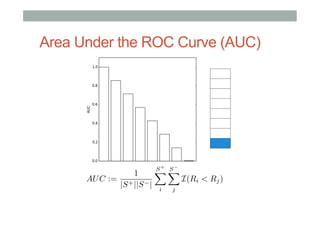
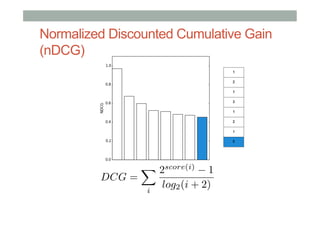
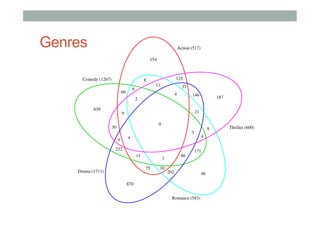
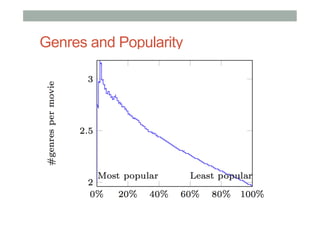
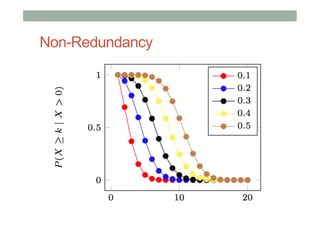
The document discusses ranking and diversity in recommender systems, emphasizing the importance of accurate ranking and the challenges involved, such as learning to rank directly rather than predicting ratings. It outlines various ranking methods, potential inconsistencies, and the need for diversity in recommendations through techniques like intent-aware metrics and genre-based diversity. Additionally, it introduces new diversity metrics based on the binomial distribution and highlights coverage and redundancy considerations in recommendation algorithms.

1. RANKING AND DIVERSITY
IN RECOMMENDATIONS
Alexandros Karatzoglou
@alexk_z

2. Thanks
Linas Baltrunas
Telefonica
Yue Shi
TU Delft
Saul Vargas
Universidad Autonoma de Madrid
Pablo Castells
Universidad Autonoma de Madrid

3. Telefonica Research in Barcelona
• User Modeling: Recommender Systems
• Data Mining, Machine Learning
• Multimedia Indexing and Analysis
• HCI
• Mobile Computing
• Systems and Networking
• http://www.tid.es

4. Recommendations in Telefonica

5. People You May Know@Tuenti

6. Recommendations in Telefonica

8. Firefox OS Marketplace

9. Collaborative Filtering
+
+
+
+
+
+
+
+
X ↵ik
fij = hUi Mj i i
hUk Mj i
, Mj +
|Fi |
+
k2Fi

10. Tensor Factorization
CP-Decomposition
HOSVD
Fijkijk S ⇥U Ui ,⇥M j , CkC Ck
F = = hU i M Mj ⇥ i
Karatzoglou et al. @ Recsys 2010

11. Publications in Ranking
CIKM 2013: GAPfm: Optimal Top-N Recommendations for Graded Relevance Domains
RecSys 2013: xCLiMF: Optimizing Expected Reciprocal Rank for Data with
Multiple Levels of Relevance
RecSys 2012: CLiMF: Learning to Maximize Reciprocal Rank with Collaborative
Less-is-More Filtering * Best Paper Award
SIGIR 2012: TFMAP: Optimizing MAP for Top-N Context-aware Recommendation
Machine Learning Journal, 2008: Improving Maximum Margin Matrix Factorization
* Best Machine Learning Paper Award at ECML PKDD 2008
RecSys 2010: List-wise Learning to Rank with Matrix Factorization for Collaborative Filtering
NIPS 2007: CoFiRank - Maximum Margin Matrix Factorization for Collaborative Ranking

12. Recommendations are ranked lists

13. Popular Ranking Methods
• In order to generate the ranked item list, we need some
relative utility score for each item
• Popularity is the obvious baseline
• Score could depend on the user (personalized)
• Score could also depend on the other items in the list (list-wise)
• One popular way to rank the items in RS is to sort the
items according to the rating prediction
• Works for the domains with ratings
• Wastes the modeling power for the irrelevant items

14. Graphical Notation
Relevant
Irrelevant
Irrelevant
Irrelevant
Irrelevant
Irrelevant
Relevant
Relevant

15. Ranking using latent
representation
• If user = [-100, -100]
• 2d latent factor
• We get the corresponding ranking

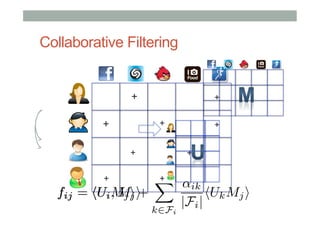
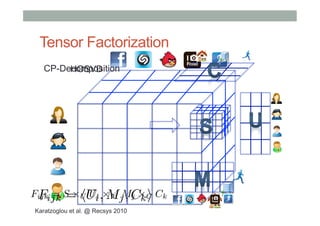
16. Matrix Factorization
(for ranking)
• Randomly initialize item vectors
• Randomly initialize user vectors
• While not converged
• Compute rating prediction error
• Update user factors
• Update item factors
• Lets say user is [-100, -100]
• Compute the square error
• (5-<[-100, -100], [0.180, 0.19]>)2=1764
• Update the user and item to the direction
where the error is reduced
(according to the gradient of the loss)
8 items with ratings
and random factors

17. Learning: Stochastic Gradient
Descent with Square Error Loss

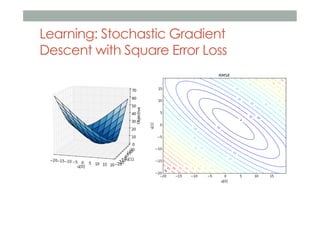
18. SquareUser: [3, 1], RMSE=6.7
Loss

19. Learning
to
Rank
for
Top-­‐k
RecSys
• Usually
we
care
about
accurate
ranking
and
not
ra=ng
predic=on
• Square
Error
loss
op=mizes
to
accurately
predict
1s
and
5s.
• RS
should
get
the
top
items
right
-­‐>
Ranking
problem
• Why
not
to
learn
how
to
rank
directly?
• Learning
to
Rank
methods
provide
up
to
30%
performance
improvements
in
off-­‐line
evalua=ons
• It
is
possible,
but
a
more
complex
task

20. Example: average precision (AP)
• AP: we compute the precision at each relevant position
and average them
AP =
|S|
X
P (k)
k=1
|S|
P@1+ P@2 + P@4 1 /1+ 2 / 2 + 3 / 4
=
= 0.92
3
3

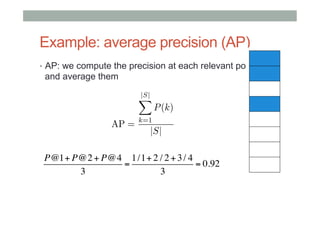
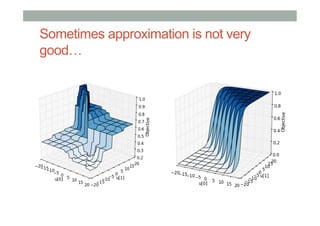
21. Why is hard? Non Smoothness
Example: AP
u:[-20,-20]
u:[20,20]

22. AP vs RMSE

23. The Non-smoothness of
Average Precision
AP =
|S|
X
P (k)
k=1
|S|
APm = PN
1
i=1
ymi
N
N
X ymi X
i=1
rmi
j=1
ymj I(rmj  rmi )
ymi
is 1 if item i is relevant for user m and 0 otherwise
I(·)
indicator function (1 if it is true, 0 otherwise)
rmi Rank of item i for user m

24. How can we get a smooth-AP?
• We
replace
non
smooth
parts
of
MAP
with
smooth
approxima=on
1
rmi
⇡ g(fmi ) = g(hUm , Vi i)
g(x) = 1/(1 + e
x
)

25. How can we get a smooth-MAP?
• We
replace
non
smooth
parts
of
MAP
with
smooth
approxima=on
I(rmj  rmi ) ⇡ g(fmj
fmi ) = g(hUm , Vj
Vi i)
g(x) = 1/(1 + e
x
)

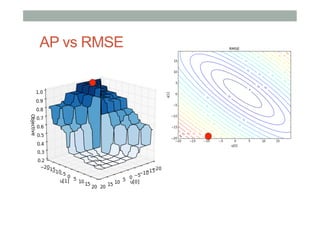
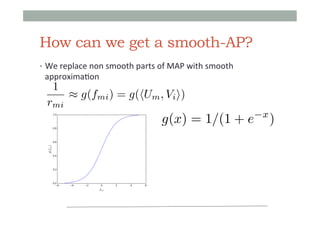
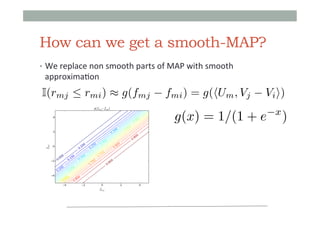
26. Smooth version of MAP
u:[-20,-20]
u:[20,20]

27. Sometimes approximation is not very
good…

28. Ranking Inconsistencies
• Achieving a perfect ranking for all users is not possible
• Two Sources of Inconsistencies:
• 1) Factor Models (all models) have limited expressive
power and cannot learn the perfect ranking for all users
• 2) Ranking functions approximations are inconsistent e.g.
A >B & B>C but C > A

29. Summary on Ranking 101

30. Area Under the ROC Curve (AUC)
1
AU C := +
|S ||S |
S+ X
XS
i
j
I(Ri < Rj )

31. Reciprocal Rank (RR)
1
RR :=
Ri

32. Average Precision (AP)
AP =
|S|
X
P (k)
k=1
|S|

33. AP vs RR

34. Normalized Discounted Cumulative Gain
(nDCG)
DCG =
X 2score(i)
i
1
log2 (i + 2)

35. Relevance solved! Is that all?
• Ranking “solves” the relevance problem
• Can we be happy with the results?

36. Relevance solved! Is that all?
• Coverage
• Diversity
• Novelty
• Serendipity

37. Diversity in Recommendations
• Diversity using Genres
• Movies, Music, Books
• Diversity should fulfill:
• Coverage
• Redundancy
• Size Awareness

38. Diversity methods for RecSys
• Topic List Diversification or
• Maximal Margin Relevance
fM M R (i; S) = (1
) rel(i) +
min dist(i, j)
j2S

39. Diversity methods for RecSys
• Intent-Aware IR metrics
ERR
IA =
X
s
p(s)ERR

40. Example
Action
Comedy
Sci-Fi
Western
Action
Thriller
Sci-Fi
Western
Adventure
Western

41. Genres
Action (517)
154
Comedy (1267)
125
8
11
6
60
37
4
146
2
639
187
21
9
0
30
8
3
9
4
4
232
171
11
1
75
Drama (1711)
86
10
202
870
Romance (583)
46
Thriller (600)

42. Genres and Popularity

43. Binomial Diversity
• We base a new Diversity Metric on the Binomial
Distribution
✓ ◆
N k
P (X = k) =
p (1
k
p)
N
k

44. User Genre Relevance
• Fraction of Items of genre “g” user interacted
with
Iu
p00
g
kg
=
|Iu |
• Global fraction of items of genre “g”
• Mix
P Iu
u kg
0
pg = P
u |Iu |
pg = (1
↵)
0
pg
+↵
00
pg

45. Coverage
• Product of the probabilities of the genres not represented
in the list not being picked by random
Coverage(R) =
Y
g 2G(R)
/
P (Xg = 0)
1/|G|

46. Non-Redundancy
P (Xg
k | Xg > 0) = 1
N onRed(R) =
Y
g2G(R)
k 1
X
l=1
P (Xg
P (Xg = l | Xg > 0)
R
kg | Xg > 0)1/|G(R)|

47. Non-Redundancy

48. Binomial Diversity
BinomDiv(R) = Coverage(R) · N onRed(R)

49. Re-Ranking
• Re-Rank based on Relevance and Binomial Diversity
fBinomDiv (i; S) = (1
) normrel (rel(i)) + normdiv (div(i; S))
normX (x) =
x
µX
X

50. Example

51. Thanks!
• Questions?