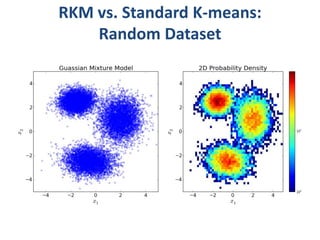
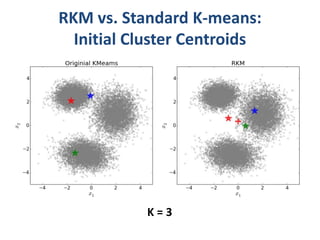
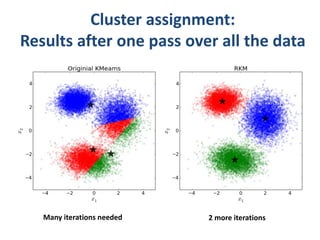
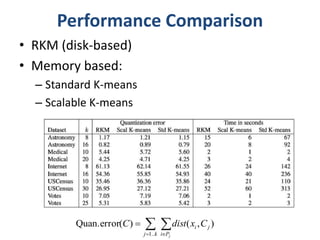
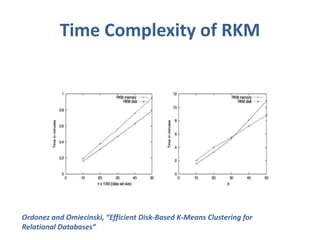
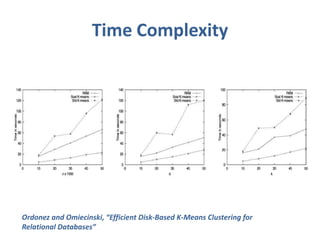
This document discusses clustering algorithms for large datasets that do not fit into main memory. It introduces the Relational K-Means (RKM) algorithm, which limits disk I/O by assigning data points in batches and updating cluster centroids after only 3 iterations. RKM stores cluster assignment and centroid data in matrices on disk and minimizes I/O by accessing matrix rows sequentially. An evaluation shows RKM outperforms standard K-means on large datasets due to its ability to handle data that does not fit in memory through efficient disk access. However, RKM does not address all limitations of K-means clustering.

1. Clustering on Database Systems
Vahid Mirjalili
Michigan State University

2. Clustering
• Partitioning data into groups
Items in the same group should have higher similarity to each
other than items from different groups
• A similarity/dissimilarity measure
• Examples:
 Clustering patients in a hospital
 Genomic clustering
 Hand-written character recognition
A. Jain, “Data Clustering: 50 years beyond K-means”

3. Clustering vs. Classification
Reinforcement
learning
Predictive Modeling Tasks
Unsupervised
Learning
• Classification is supervised
Supervised
Learning
– class labels are provided;
– learn a classifier to predict class labels of novel/unseen
data
• Clustering is unsupervised or semi-supervised;
– No class label is give
– Understand the structure underlying your data

4. Clustering Approaches
 Probability-based
– Assuming statistical independence among features
– Inefficient updating and storing clusters
 Distance-based
– Assuming direct access to all data points
– Hierarchical clustering: O(N2), not giving the best clustering

5. Distance-Based Clustering Algorithms
• kmeans and its variants (kmedoids, kernel
kmeans, fuzzy c-means, …)
• Density based methods (DBSCAN)
• Hierarchical methods

6. Challenges
• Unknown number of clusters (from 1 to N)
Input data K=2 K=6
You always get some
output as clusters
Are they really distinct
clusters?
A. Jain, “Data Clustering: 50 years beyond K-means”

7. Challenges
• Clusters with different shapes, sizes and
densities
Shapes: globular shape, linear vs. non-linear
shapes
A. Jain, “Data Clustering: 50 years beyond K-means”

8. Standard K-Means Algorithm
• Find initial Cluster centroids randomly
• An iterative algorithm
1. Assignment step: assign each data point the
cluster whose mean is closest (smallest distance)
2. Update step: update the mean (centroid) of each
cluster
Distance: squared Euclidean distance
( , ) 
dist x   x 

j j  1 

Centroid: mean of feature vectors 


i C

i
C
X
N
2
 
1
d
j

9. Standard K-Means Algorithm

10. Problem in Database-oriented
Clustering
• Low memory available compared to size of
dataset  data doesn’t fit in main memory
• High I/O
• Necessary to avoid too many iterations

11. RKM: An Efficient Disk-based KMeans
Method
• Find the initial centroids by
• Only 3 iterations:
r d c all      /
– Assign every L points to nearest centroids;
– Update the cluster centroids
• Minor efficiency tricks:
N L 
– Keep track of LS, SS and Nc for each cluster during
assignment  update step:
c c   LS / N

12. Implementation of RKM:
storing data matrices
• D  input dataset
• Pj
 cluster j (for j in [1..k])
• Mj, Qj, Nj
 Linear Sum, Squared Sum, cluster
size
• Cj, Rj, Wj
 Centroids, Variances, Weights
(accessed during update step)
C 
M /
N
j j j
R  Q / N 
M M /
N



j j l
l k
j
t
j j j j j
W N N
1..
2
/

13. RKM avoids local minima:
split large clusters
• Only performed if size of a cluster is less than
a user-defined threshold
1. Remove the centroid of the small cluster
2. Find the largest cluster (largest Wj)
3. Randomly choose two centroids for the largest
cluster (using Cj, and Rj)
4. Reassign the items of small and large clusters

14. RKM vs. Standard K-means:
Random Dataset

15. RKM vs. Standard K-means:
Initial Cluster Centroids
K = 3

16. Cluster assignment:
Results after one pass over all the data
Many iterations needed 2 more iterations

17. RKM: Database design
• Relational schema for sparse data
representation: D(pid, inx, value)
• For other matrices: doing 1 I/O per matrix row
to minimize I/O
Matrix access
E step (assignment step)
M step (update step)
Ordonez and Omiecinski, “Efficient Disk-Based K-Means Clustering for
Relational Databases”

18. Performance Comparison
• RKM (disk-based)
• Memory based:
– Standard K-means
– Scalable K-means
 
 
C dist x C
Quan.error( ) 
( , )
j k i P
i j
j
1..

19. Time Complexity of RKM
Ordonez and Omiecinski, “Efficient Disk-Based K-Means Clustering for
Relational Databases”

20. Time Complexity
Ordonez and Omiecinski, “Efficient Disk-Based K-Means Clustering for
Relational Databases”

21. Conclusion
• RKM resolve some of the limitations of K-means
• RKM limits disk access (I/O)
• Final clustering is achieved with 3 iterations
• On large datasets RKM outperforms standard K-means
• Other limitations of K-means clustering still
remain

22. Read more …
General implementation in IPython notebook:
http://goo.gl/YZScH9
http://www.vahidmirjalili.com