This document summarizes key concepts in engineering mechanics and strength of materials for mechanical engineering students. It covers topics like force equilibrium, stress and strain analysis, material properties, and failure theories. Key equations are presented for areas including static equilibrium, centroids, moments of inertia, stress-strain relationships, transformation of stresses, and bending stresses in beams. Diagrams illustrate stress distributions and Mohr's circle analyses for various loading conditions.

1. Design Fundamentals
for Mechanical
Engineering Students

2. Engineering Mechanics – Important points and equations
Force in three dimension are unit vectors
= ; = ; = ;
Static Equilibrium equations
Equilibrium of rigid bodies in two dimensions
∑Fx = 0; ∑Fy = 0; ∑Mz = 0
Equilibrium of rigid bodies in three dimensions
∑Fx = 0; ∑Fy = 0; ∑Fz = 0
∑Mx = 0; ∑My = 0; ∑Mz = 0
Lami’s theorem
When three concurrent coplanar forces
are acting at a point are in equilibrium,
then each force is directly proportional to
the sine of the angle between the other
two forces.
= =
Parallelogram law
“When two forces acting at a point can be
represented as sides of a parallelogram
then the diagonal represents the resultant
of two forces”.
Resultant R= + +
Angle between resultant and F1
α =

3. Triangle law
“When two forces acting at a point can be
represented as sides of a triangle then the
closing side is the resultant”.
= =
Where R  Resultant
Support reactions
For fixed support  Rx, Ry and Mreaction
For roller support  Ry
For hinged support  Rx and Ry
Where
Rx  reaction in x – direction
Ry  reaction in y – direction
Mr  reaction moment
Ball and socket joint gives three reaction forces.
Fixed support gives three reaction forces and three reaction moments.
The principle of transmissibility is applicable only for rigid bodies not for deformable
bodies
Properties of surfaces
First moment of area about the centroidal axes is zero.
The unit for first moment of area is mm3
.
Centroid for standard cross-sections
For rectangle = b/2 ; = h/2
For right angle triangle = b/3 ; = h/3
(Note: vary with respect to orientation of
triangle)
For circle = = d/2
For semicircle = d/2; = 4r/3π
(Note: vary with respect to orientation of
semicircle)
For quadrant = = 4r/3π
(Note: vary with respect to orientation of

4. semicircle)
Papus and Guldinus theorem I and II
Surface area of revolution
A = 2π .L (or) A = 2π .L
Volume of revolution
V = 2π .A (or) V = 2π .A
Area moment of inertia for various sections
IXX = ∫ dA
Iyy = ∫ dA
Ixy = ∫
Where Ixx, Iyy, Izz  second moment of area
(or) area moment of inertia
The unit for area moment of inertia is mm4
.
For Rectangle IXX = ; IYY =
For Isosceles triangle IXX = ; IYY =
Right angled triangle IXX = ; IYY =
Circle IXX = IYY =
Hollow circle IXX = IYY = [ − ]
Semicircle IXX = 0.1098 r4
; IYY = d4
Quadrant IXX = IYY = 0.055 r4
Parallel axis theorem
IAB = IG + Ah2
Where IAB  Moment of inertia about the
AB axis which is parallel to centroidal axis
IG  Moment of inertia about centroidal
axis
Parallel axis theorem for product moment
of inertia
IXY = Ix’y’ + Axy
Perpendicular axis theorem
IZZ = J = IXX +Iyy
[Note: Twisting a member is more difficult
than bending]
Where IZZ = J = Polar moment of inertia

5. IZZ =
Product moment of inertia
Ixy = ∫
For symmetrical section Ixy = 0
For unsymmetrical sections Ixy ≠ 0
(It may be positive or negative)
Mass moment of inertia for various solids
I = ∫
Rectangular disc Izz =
( )
IXX =
( )
; IYY =
( )
Solid thin circular disc
IXX = IYY = ; Izz =
Circular rod Ixx = Iyy =
Solid cylinder Izz =
Ixx = Iyy = [3r2
+h2
]
Sphere IXX = IYY = IZZ =
Radius of gyrations
For area K = ; where I = Area moment
of inertia
For mass K = ; where I = mass moment
of inertia
Basic laws of friction
When the body is about to start,
Friction force = μ × normal reaction
Fmax = μ N
Where F  Limiting friction (or) maximum
friction force at static condition
μ  coefficient of friction

6. N  normal reaction
For static condition, Fs = μs N
For dynamic condition, Fk = μk N
μs  coefficient of static friction
μk  coefficient of kinetic friction
Always μs > μk
Angle of friction ϕ =
Always ϕs > ϕk
ϕs  angle of static friction
ϕk  angle of kinetic friction
Friction in the belt drives
= (for flat belt drive) ;
μ  coefficient of friction
θ  angle of contact
= (for V belt drive)
α  groove angle
Power P = (T1 – T2)×Velocity
Torque T = (T1 – T2) × Radius of pulley
Condition for maximum power transmission on belt drive Tmax = 3Tc = 3mv2
Tmax = Maximum tension in the tight side = T1 + Tc
Tc = Centrifugal tension
Trusses
If m + 3 = 2j, then the truss is statically determinate structure
If m + 3 > 2j, then the truss is redundant structure (statically indeterminate structure)
[more members than independent equations]
If m + 3 < 2j, then the truss is unstable structure (will collapse under external load)

7. [deficiency of internal members]
For statically determinate trusses, ‘2j’ equations for a truss with ‘j’ joints is equal to m+3
(‘m’ two force members and having the maximum of three unknown support reactions).
Dynamics
Fundamental equation for dynamics
For linear motion; Force F = ma
For angular motion; Torque T = Iα
Where m  Mass; a  Acceleration; I 
Mass moment of inertia; α  Angular
acceleration
Equations of motion (linear and angular)
Linear motion
v = u + at
v2
= u2
+ 2as
s = ut +
Angular motion
= + αt
= + 2αθ
θ = +
Projectile motion
Range; R =
Maximum range; R max = for α = 45°
Maximum height; h = sin2
α
Time of flight; t =
Equation of projectile
y = (tanα) x – ( ) (sec2
α) x2
Curvilinear motion
at  tangential acceleration
an  normal acceleration
D’ Alembert’s principle
(Dynamic equilibrium equation)
F – ma = 0
ma  Inertia force

8. Work energy equation
Work done = change in kinetic energy
∑F × distance = [mv1
2
– mv2
2
]
Rotational Kinetic energy =
Impulse momentum equation
Impulse = Change in momentum = Final
momentum – Initial momentum
∑F × Δt = mv - mu
Impact of elastic bodies
Initial momentum before impact = final
moment after impact
m1u1 + m2u2 = m1v1 + m2v2
Coefficient of restitution
e =
If e = 0, then perfectly plastic impact
If e = 1, then perfectly elastic impact
General Plane Motion  Motions in which all the particles of the body move in parallel
planes. Any plane motion which is neither a rotation nor a translation is referred to as a
general plane motion.
Examples of general plane motion :
When a rigid body is in translation, all the points of the body have the same velocity and
the same acceleration at any given instant.
For any body undergoing planar motion, there always exists a point in the plane of motion
at which the velocity is instantaneously zero. This point is called the instantaneous center of
rotation, or C. It may or may not lie on the body.

9. Instantaneous centre of a body rolling with sliding on a stationary curved surface lies on
the common normal at the point of contact.

10. Strength of materials – Important points and equations
 Axial stress and bending stresses are out of plane stresses. Shear stresses are in
plane stresses.
 In uniaxial loading, maximum normal stress (σ) will be in a plane at θ= 0°
(Principal plane). Maximum shear stress (τ max) will be in a plane of θ= 45°
 In uniaxial loading, maximum shear stress τmax = 0.5 σmax
 Ductile materials are weak in shear plane. Brittle materials are weak in normal
plane.
Direct Stress (or) Axial Stress = =
Uniaxial loading
Single shear
= =
Double shear
= =
( )

11. Hooke’s law
Within the elastic limit,
Stress α Strain  σ = E ε
Shear stress α Shear strain  τ = CØ
Where
σ  stress
E  Young’s modulus
ε  strain
τ  shear stress
C or G  modulus of rigidity or shear modulus
Ø  shear strain
Strain
Strain ε =
 change in length
 original length
Change length δl =
Strain has no unit. The unit for strain in mm/mm.
Poisson’s ratio γ =
Materials which give negative Poisson’s ratio are anti-rubber, dilational materials, or
auxetic materials or auxetics.
Elastic constants
E = Young’s modulus
C = Shear modulus
K = Bulk modulus
Poisson’s ratio = γ
E = 3K (1 - 2 γ)
E = 2C (1+ γ)
E =
Bulk modulus K =

12. Compound bar
 Change in length is equal for unequal length bars.
 Both strain and change in length is equal for equal
length bars
Elongation of a bar due to
self-weight
Change in length dl = (for prismatic bar)
Change in length dl = (for conical bar)
Principle of super position
(when a number of loads are
acting on a body, the
resulting strain will be the
algebraic sum of strains
caused by the individual
loads)
Change in length dl = + +
= + +
= − −
= − −
= − −
Thermal stress
σthermal = α. ΔT. E
Thermal stress is zero if there is no resistance to expansion
in a component subjected to temperature change.
Free bar (No resistance to deformation) under change in its
temperature will not induce any stress.
A bar which has resistance to deformation will lead to the
formation of thermal stress under change in its
temperature.
Regions of stress strain curve

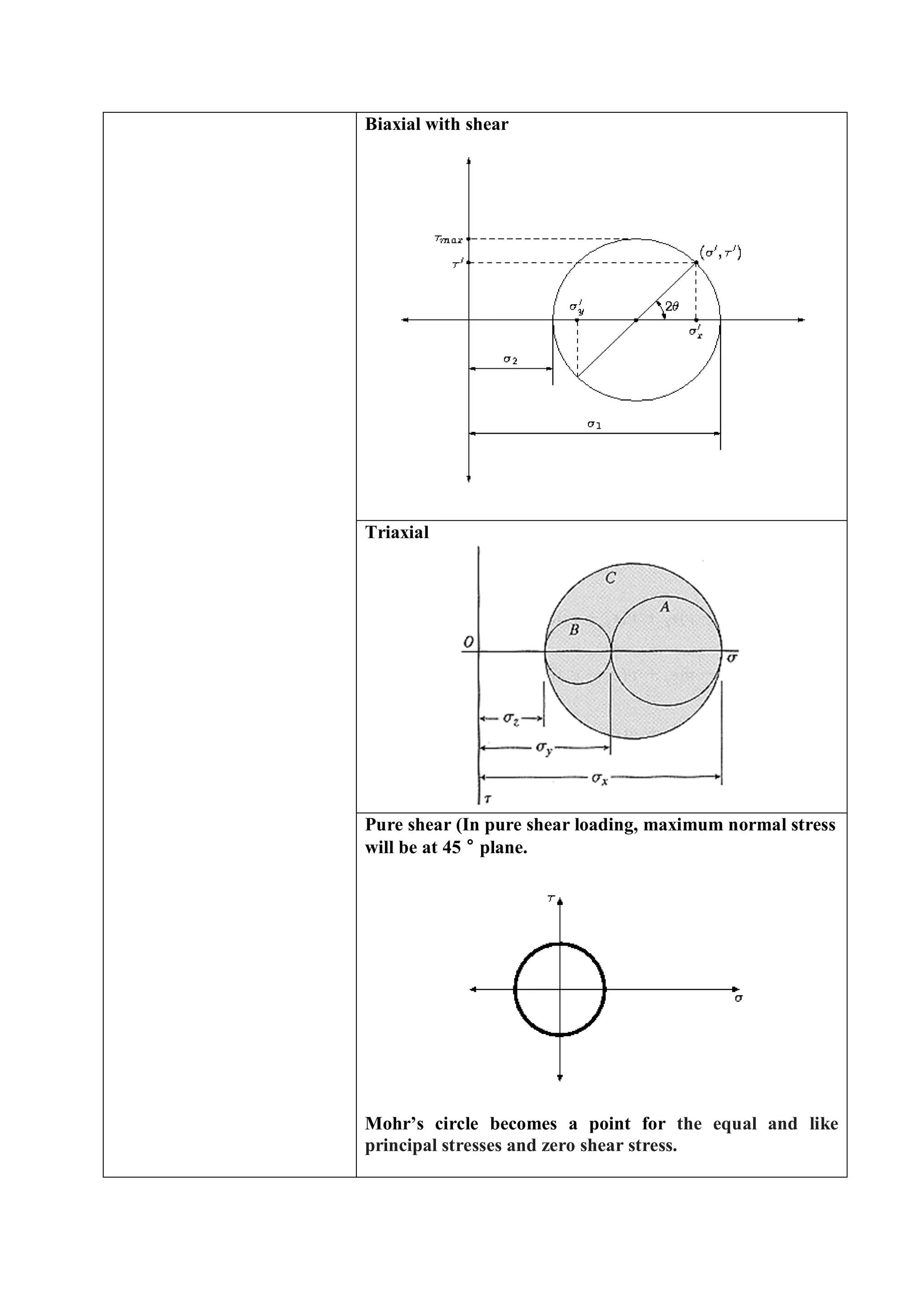
13. Plane stresses and plane
strain
For plane stress (Stress in third direction is zero)
σx ≠ 0 σy ≠ 0 τxy ≠ 0
σz = 0, τxz = 0, τyz = 0 but εz ≠ 0
For plane strain (Strain in third direction is zero)
εz = 0, γxz = 0, γyz = 0
σz ≠ 0, τxz ≠ 0, τyz ≠ 0
Transformation equations
Normal stress
σn = τxy sin2θ + + ( ) cos2θ
Shear stress
τ = ( ) sin 2θ - τxy cos2θ
Principal stresses and
principal planes
A plane which has maximum
normal stress is called
principal plane.
The value of shear stress in
principal plane is zero.
σ 1,2 = ± [ ] +
tan 2θp =

14. τ1,2 = ± [ ] +
tan 2θs =
Strain energy (U)
U = =
U =
Relation between bending
moment, shear force and
loading
W = load, V = shear force, M = moment
W =
V =
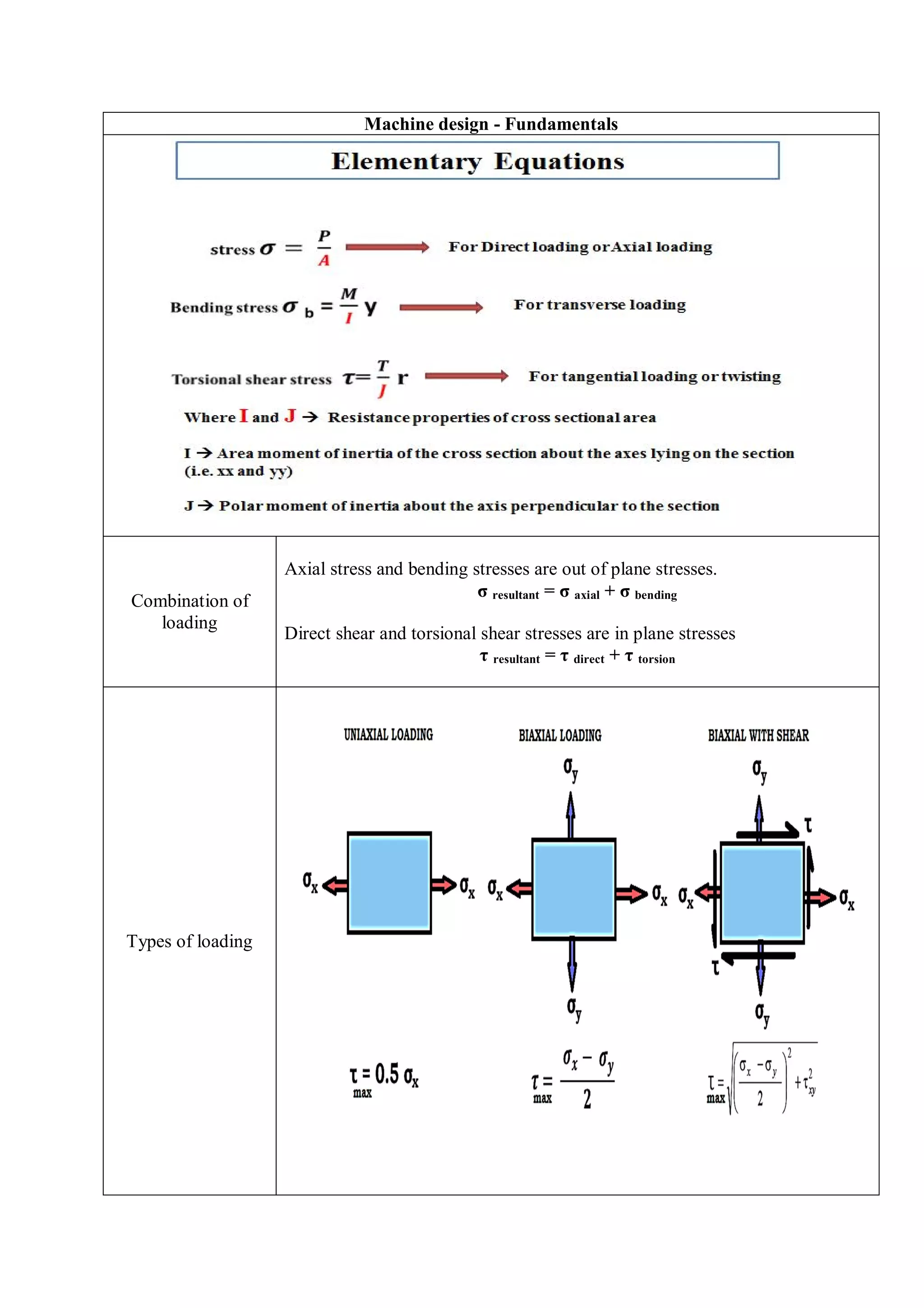
Bending Equation
= =
Bending stress
σb =
M  bending moment
I  Area moment of inertia
y  distance from the neutral axis to the extreme fiber
E  Young’s modulus
R  Radius of curvature
Pure bending: A beam section which undergoes only
bending stress with zero shear stress is called as pure
bending.
Sagging bending moment (Positive BM)  concavity on the top surface of beam
Hogging bending moment (Negative BM)  convexity on the top surface of beam
The point where bending moment (BM) changes its sign is known as point of contraflexure.
Shear stresses in beams
τ =
. .
.
where S  shear force; A  cross-section;
 distance from the neutral axis to centroid
I  area moment of inertia
b  width of the beam

15. Shear stresses distribution
for different sections
Mohr’s circle for various
loading
Uniaxial
Biaxial

16. Biaxial with shear
Triaxial
Pure shear (In pure shear loading, maximum normal stress
will be at 45°plane.
Mohr’s circle becomes a point for the equal and like
principal stresses and zero shear stress.

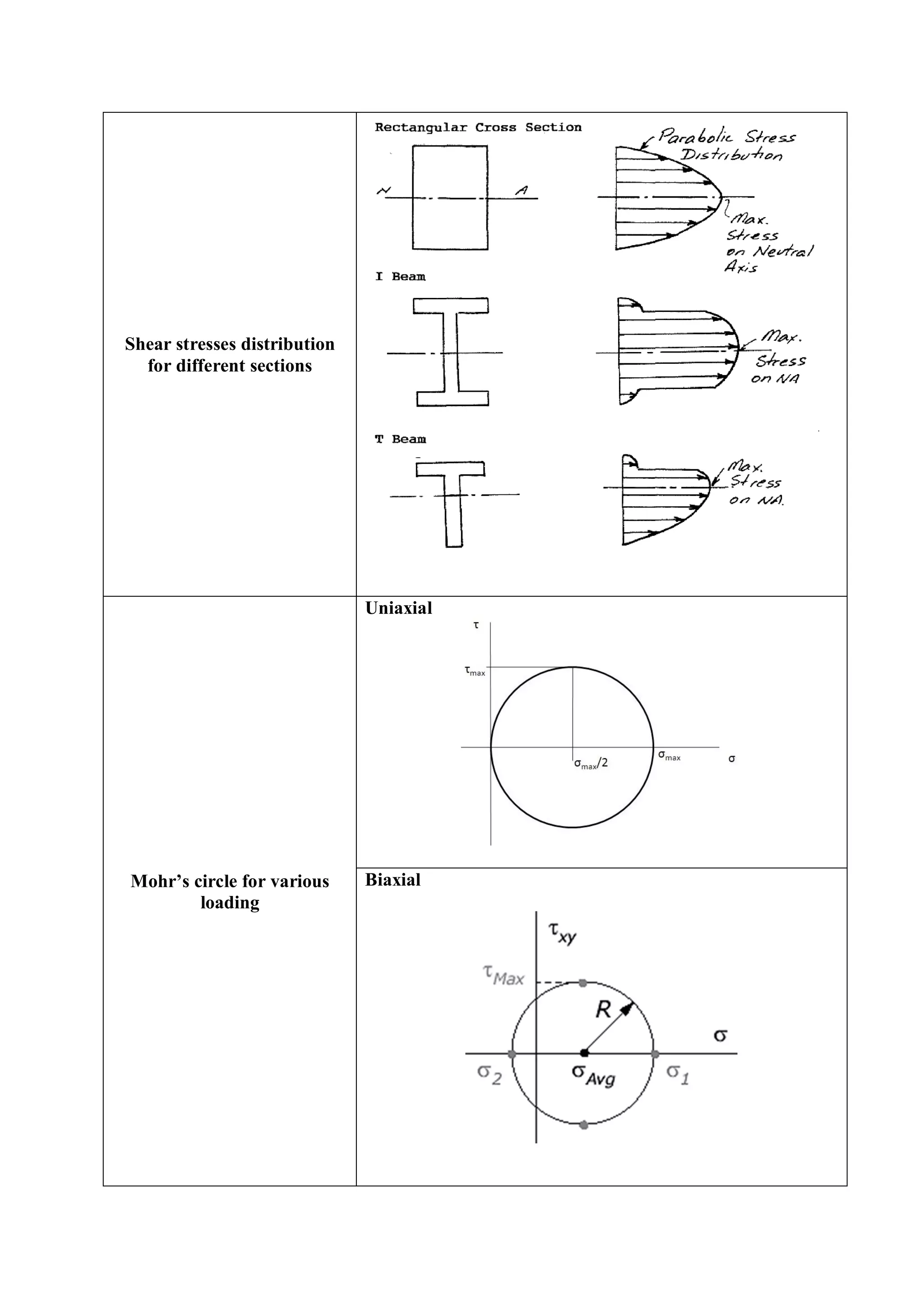
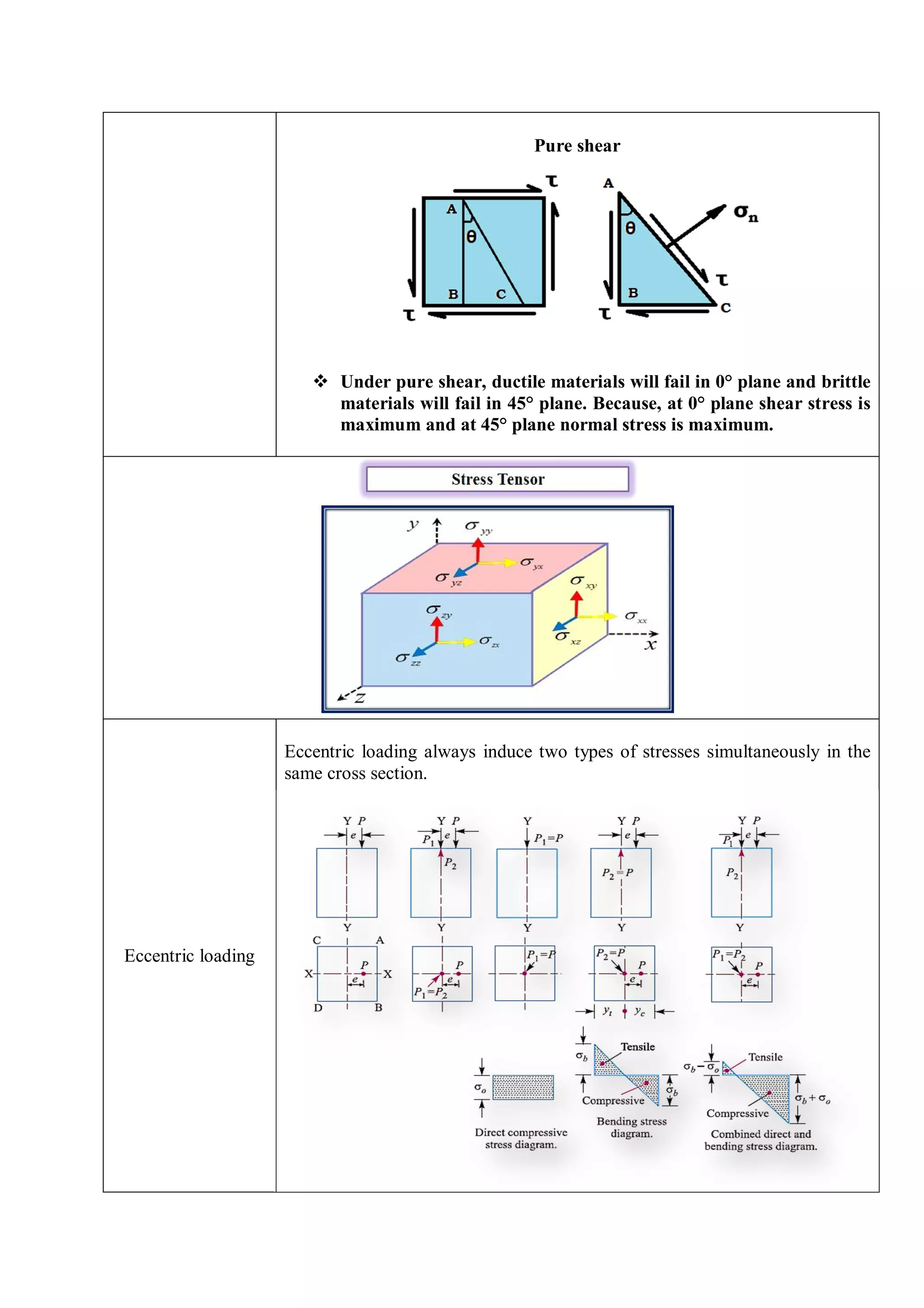
17. Torsion of circular shafts
Torsional equation
=
.
=
Strength equations
Equivalent bending moment
Me = [ + √ + ]
Equivalent twisting moment
Te = √ +
Polar moment of inertia
(resistance against twisting)
For circular cross section
J =
Torsional shear stress
distribution
Hollow shaft comparison
with solid shaft
When a shaft is subjected to a torque, torsional shear stress
will be high at the outer radius and zero at the centre.
Therefore removal of material from the center of shaft will
not affect the design. Hence, hollow shaft is better than
solid shaft.
Deflection of beams
Cantilever beam subjected to point load at the end
y =

18. Cantilever beam subjected to UDL
y =
Cantilever beam subjected to UVL
(max rate of loading at the fixed end & zero rate of loading
at the free end)
y =
(max rate of loading at the free end & zero rate of loading
at the fixed end)
y =
Simply supported beam subjected to point load at midpoint
y =
Simply supported beam subjected to UDL
y =
Simply supported beam subjected to UVL
y =
Fixed beam subjected to point load at its midpoint
y =
Fixed beam subjected to UDL
y =
Fixed beam subjected to UDL
y =
Buckling of columns
Column with hinged ends
Pe =
Column one end fixed other end free
Pe =
Column both ends fixed
Pe =

19. Column one end fixed other end hinged
Pe =
.
Slenderness ratio =
Pressure vessels
For cylindrical portion
Hoop or circumferential stress
σc =
Longitudinal stress
σl =
For spherical portion
Hoop or circumferential stress
σc =
 The thickness of the cylinder walls must be
approximately 2.4 times that of the hemispheroid
ends for no distortion of the junction to occur.
FOS (factor of safety) =  (for ductile materials)
FOS (factor of safety) =  (for brittle materials)
FOS (factor of safety) =  (for variable loading)
For constant
loading

20. Machine design - Fundamentals
Combination of
loading
Axial stress and bending stresses are out of plane stresses.
σ resultant = σ axial + σ bending
Direct shear and torsional shear stresses are in plane stresses
τ resultant = τ direct + τ torsion
Types of loading

21. Pure shear
 Under pure shear, ductile materials will fail in 0° plane and brittle
materials will fail in 45° plane. Because, at 0° plane shear stress is
maximum and at 45° plane normal stress is maximum.
Eccentric loading
Eccentric loading always induce two types of stresses simultaneously in the
same cross section.

22. Theories of failure
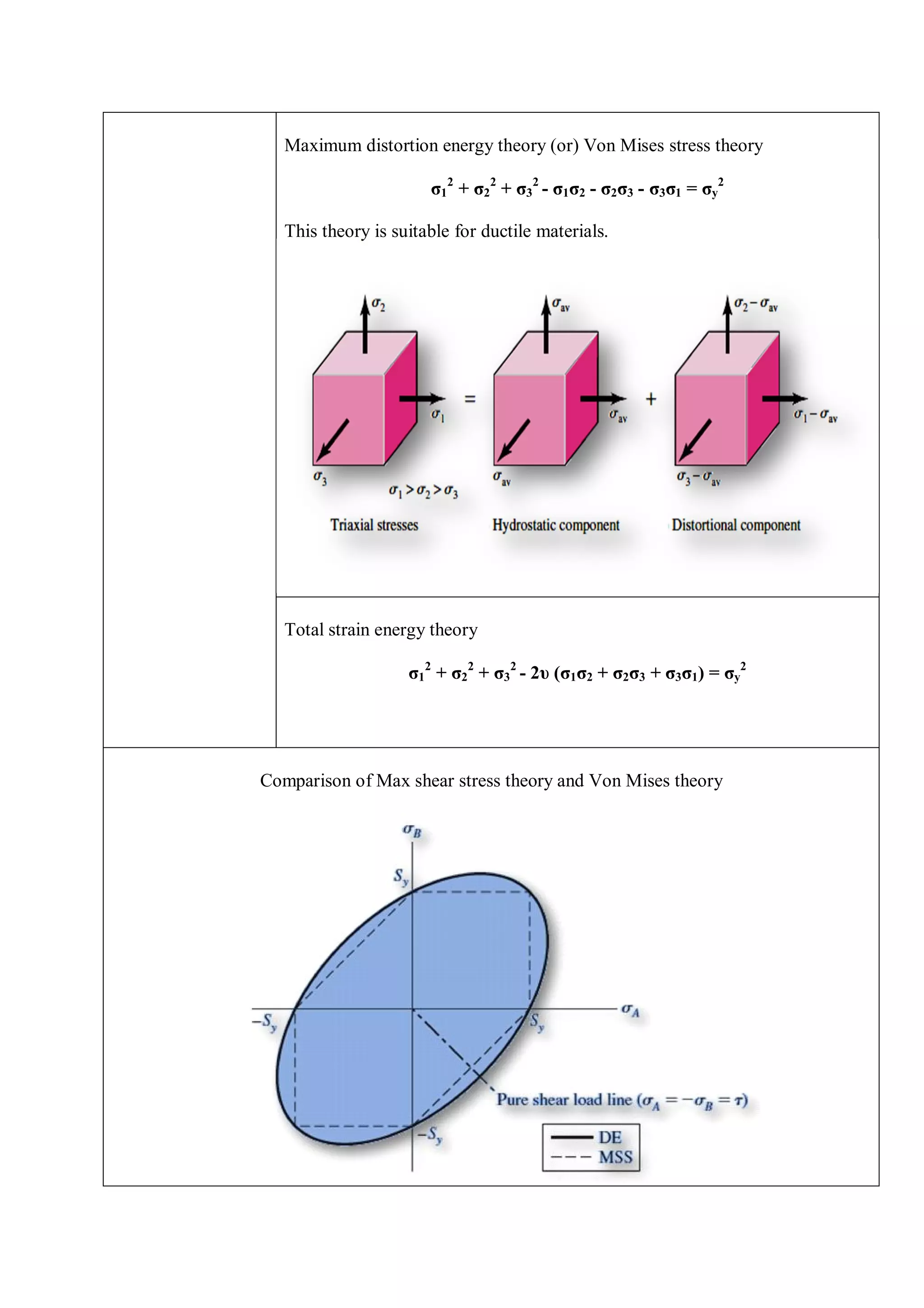
Maximum principal stress theory (Rankine’s theory)
=
Whichever is maximum
Note: Principal stress theory is suitable for brittle materials.
Maximum shear stress theory or Tresca’s criterion
[ − ] [ − ] [ − ] =
Whichever is maximum
This theory is suitable for ductile materials.
Maximum principal strain theory
− [ + ] or − [ + ] or − [ + ] =
(Whichever is maximum)

23. Maximum distortion energy theory (or) Von Mises stress theory
σ1
2
+ σ2
2
+ σ3
2
- σ1σ2 - σ2σ3 - σ3σ1 = σy
2
This theory is suitable for ductile materials.
Total strain energy theory
σ1
2
+ σ2
2
+ σ3
2
- 2υ (σ1σ2 + σ2σ3 + σ3σ1) = σy
2
Comparison of Max shear stress theory and Von Mises theory

25. Stress concentration
Theoretical stress concentration factor
Kt = =
Fatigue stress concentration factor
Kf = 1 + q[Kt – 1]
Kf = Kt for q = 1 (material is fully sensitive to notches)
Kf = 1 for q = 0 (material has no sensitivity to notches)
Notch sensitivity
q = (Kf – 1) / (Kt – 1)
q =
In general notch sensitivity varies from 0 to 1.
Types of variable
loading

26. Low cycle fatigue:
Any fatigue failure when the number of stress cycles are
less than 1000, is called low cycle fatigue.
Examples: Failure of studs on truck wheels, failure of set screws for locating
gears on shafts, short lived components like missiles.
High cycle fatigue:
Any fatigue failure when the number of stress cycles are
more than 1000, is called high cycle fatigue.
Examples: Failure of springs, ball bearings and gears that are subjected to
fluctuating stresses.
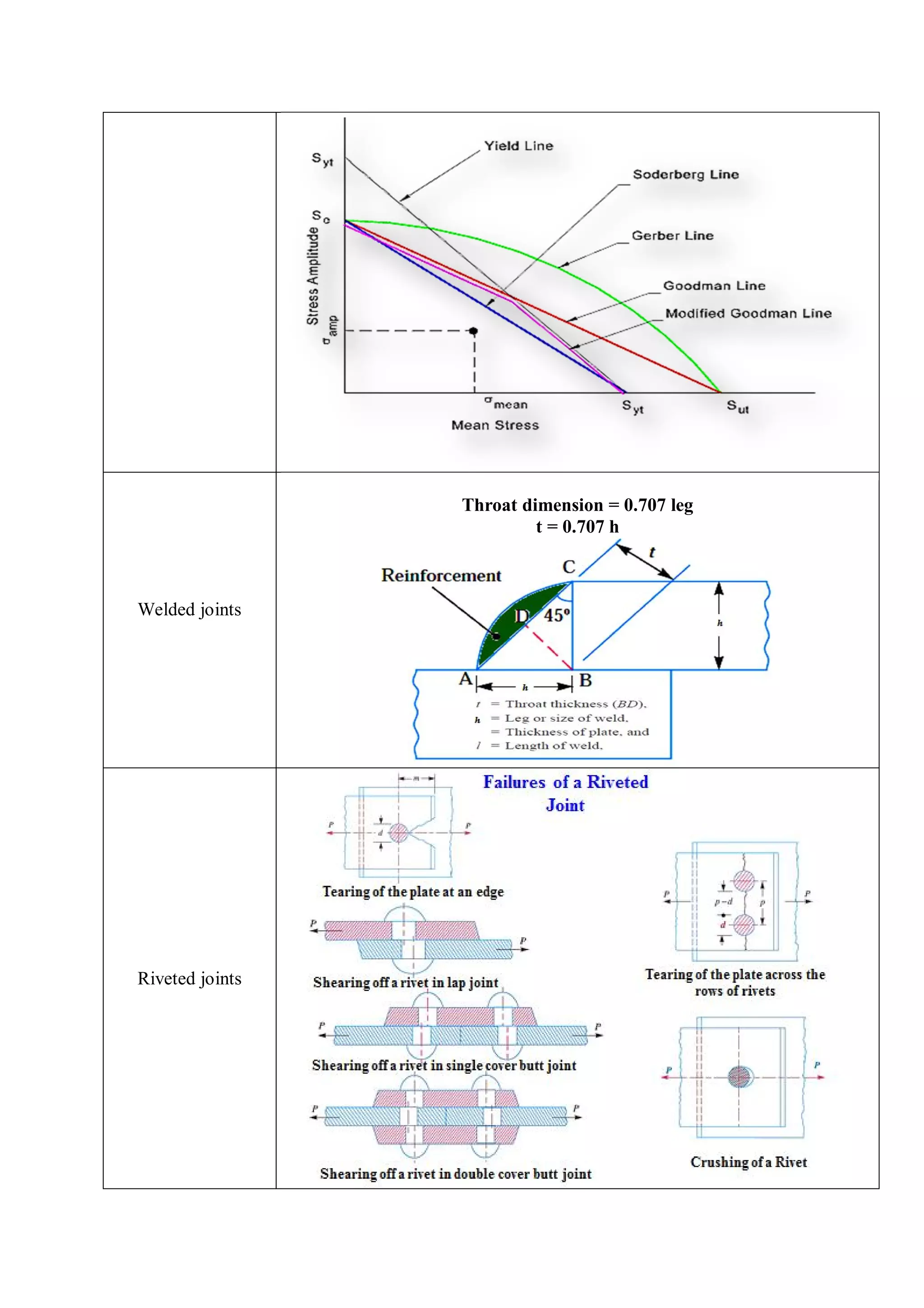
Variable loading
 mean stress;  amplitude stress
= ; =
 yield stress;  endurance limit
n  factor of safety
Soderberg line equation
+ =
 mean shear stress ;  amplitude shear stress
 yield shear strength;  endurance limit in shear
+ =
Modified Goodman line equation
[ + ] =
[ + ] =

27. Welded joints
Throat dimension = 0.707 leg
t = 0.707 h
Riveted joints

28. Design of helical
springs
Shear stress equation
τ =
Deflection of a spring
y =

29. Stiffness of a spring
q =
Strain energy stored in a spring
U =
Wahl’s factor
K = +
.
Combined stiffness (k) for springs in parallel
k = k1 + k2
Combined stiffness for springs in series
= +
Springs under
variable loading
=
−
+
Mean shear stress =
Amplitude shear stress =

30. Leaf springs
=
Deflection y =
Design of flywheel
Fluctuation of energy
ΔE = I Ks ω2

31. Coefficient of fluctuation of speed
Ks =
Rolling contact
bearing
Life of a bearing in revolutions
L = 60 × Lh × N
Dynamic load carrying capacity
Journal bearing
Sommerfield number
S = ^2

32. Materials and Manufacturing
1. Crystal structure  Ferrite (Body Centered Cubic BCC), Austenite (Face
Centered Cubic), Martensite (Body Centered Tetragonal BCT)
2. Ferrite stabilizers – Chromium, Molybdenum
3. Austenite stabilizers – Nickel, Nitrogen
4. Cementite  Fe3C (Iron carbide)
5. Pearlite ferrite + cementite
6. Bainite plate like microstructure created by austempering of steel
7. Fe-C contains less than 0.8% Carbon  hypo eutectoid steel
8. Fe-C contains greater than 0.8% Carbon  hyper eutectoid steel
9. Range of carbon percentage in steel and cast iron
Carbon percentage range for steel 0 to 2%
Carbon percentage range for cast iron  2 to 6.7%
10. Annealing  Heating the metal above recrystallization and cooling inside the
furnace itself (Also called stress relieving)
11. Normalizing Austenitizing of steel at a particular temperature
(usual normalizing temperature ranges from 815°C to 980°C) and cooling in air
12. Tempering Achieving toughness by decreasing the hardness
13. Case hardening  hardening the outer layer of steel
14. Nitriding Heat treatment that diffuses nitrogen into the surface of metal
15. Stainless steel SS 304L  18% chromium, 8% Nickel (L – stands for low carbon
less than 0.03%)
16. Function of riser  Feed molten metal to casting
17. Casting defects
Misrun  Insufficient fluidity of the molten metal; Cold shut  Two streams of
liquids are not fuse properly;

33. 18. Chills are used in casting to achieve directional solidification
19. Disposable patterns  Polystyrene
Expandable pattern  Investment casting
20. Solidification time calculation in casting
Solidification time is inversely proportional to thermal diffusivity of the mould
material
21. Diagram of casting process
22. Centrifugal casting  Impurities are collected at the inside diameter of the cast
parts  used to produce fine grain structure
23. Skim bob  To collect light impurities in the molten metal of casting;
24. Chaplets To prevent core movement due to buoyancy;
25. Green sand (Mould contains moisture) moulding  Uniform ramming leads to
greater dimensional stability of the casting
26. Negative allowance on the pattern To taken care of shake allowance
27. Shell like castings (like toys)  slush casting

34. 28. Welding shielding gases  Argon and Helium
29. Heat input per unit length of the weld
Q =
Where, E = Arc voltage; I = welding current and V = Welding speed
30. Weld polarity
DCEN (straight polarity) – High penetration (flow of current towards the work
piece) – Lower deposition rate
31. DCEP – Shallow penetration (flow of current towards the filler rod)
32. AC current – For Aluminum welding to avoid porosity (Half of the cycle
Electrode negative & half of the cycle electrode positive) oxide cleaning action
33. Aluminum welding  High tendency of oxidation
34. Non-consumable electrode – GTAW or TIG (Electrode – Tungsten)
35. Consumable electrode – MIG or GMAW, FCAW, SMAW, SAW, Electroslag
welding
36. Solid state welding – Friction Stir Welding and Friction Welding
Contamination between the surfaces in friction welding is removed by plastic
deformation
37. Metal powder used in Thermit welding  Al
38. Gas welding – Mixture of gas, types of flames and their ratio, temperature
Neutral flame oxygen and acetylene are mixed in equal amounts primary
combustion (Chemical reaction between oxygen and acetylene in the inner cone)
 products of primary combustion (CO and H2) react with O2 and forms CO2
and H2O  secondary combustion area (protection envelop) preventing
oxidation. Inner cone temperature 3200°C
39. Reducing flame  excessive acetylene  greenish acetylene feather between
inner and outer envelope  used for welding aluminum alloys and carbon steel

35. 40. Oxidizing flame  excessive oxygen  presence of unconsumed oxygen  used
for welding brass  because copper oxide covers the weldment and prevents
zinc evaporation from the weldment
41. Power beam welding process – LBW, EBW (vacuum process) – Less HAZ (heat
affected zone)  faster welding processes
42. Autogeneous welding – Welding thin plates without filler metal  Friction
welding, diffusion welding, friction stir welding
43. Submerged arc welding – Arc submerged inside the flux
44. Resistance welding spot and seam welding – Nugget formation (Force + Current)
45. Weld defects
Lack of deposition  higher welding speed & low melting rate of the filler
Lack of penetration  Low heat input, higher welding speed, incorrect weld
groove geometry, Heat transfer through molten weld pool is lesser when
compared with perpendicular direction to welding.
Over deposition  more heat input, more HAZ due to extra metal deposition
Arc strike  Damage on the parent material resulting from the accidental
striking of an arc outside the weld area
Spatters (metal droplets)  Spatters have to be removed because corrosion will
start from spatters. Porosity is possible in the weldment.

36. Undercut  Excessive current, causing the edges of the joint to melt and drain
into the weld; this leaves a drain-like impression along the length of the weld.
Surface cracks  Cracks will lead to poor ductility, Due to high Sulphur and
carbon contents, Due to martensite structure formation, Presence of Hydrogen
Slag inclusion  This type of defect usually occurs in welding processes that use
flux, such as shielded metal arc welding, flux-cored arc welding, and submerged
arc welding
Porosity  Due to entrapment of gases in the solidifying weld metal  Gases
come in the weldment from flux constituents, shielding gases, absorbed moisture,
gases dissolved in the metal itself  Surface contaminations
Lamellar tearing  It’s a cracking problem caused by the presence of elongated
inclusions (Sulphides of Mn and Fe), which are deformed in the direction of
rolling or extrusion. Stresses formed during welding lead to debonding of theses
inclusions from the matrix resulting in the formation of microcracks. During
multipass welding, microcracks leading to cracking. This cracking takes place
only in the base metal, even away from the HAZ.
46. Single point cutting tool  Tool having only one cutting point or edge tool
used for turning, boring, shaping and planning are single point cutting tools and
tool bits
47. Multipoint cutting tool  Tool having more than one cutting point or edge 
milling cutters, drill bits, reamers, saw blades, broaches
48. Cutting tool nomenclature
Back rack angle – side rack angle – end relief angle – side relief angle – end
cutting edge angle – side cutting edge angle – nose radius
49. Large positive rack angle for cutting tool  To reduce the cutting force
50. Negative rack angles are used for carbide tool materials.
51. Diamond cutting tools are not recommended for machining ferrous metals due to
chemical affinity.
52. Merchant circle diagram and related formulas

37. 53. Tool failure – what are crater and flank failure?
Crater wear starts at some distance from the tool tip because at that point chip
tool interface temperature is maximum.
54. Most of the metal cutting heat goes into the Chip. Friction at the tool chip
interface can be reduced by increasing the cutting speed.
55. Orthogonal cutting cutting edge is normal to the tool feed; two dimensional
cutting (only two force components are there i.e. cutting force and thrust force;
shear force acts on a smaller area
56. Oblique cutting cutting edge is inclined at an acute angle to the tool feed; three
dimensional cutting (three force components are there i.e. cutting force, radial
force and thrust force); shear force acts on a larger area

38. 57. Up milling (cutting and feed motion are in opposite direction; poor surface
finish; shorter tool life) and down milling (cutting and feed motion in same
direction; better surface finish; longer tool life)
58. Drilling (hole making process), trepanning (Producing large holes without
drilling), tapping (operation of cutting internal threads in a hole), boring
(Enlarging a hole with single point cutting tool), reaming (Finishing an existing
hole surface), counter boring (cylindrical flat-bottomed hole that enlarges
another coaxial hole), counter sinking (operation of producing a taper or cone
shape surface at the entrance of a hole).
59. Spot facing (operation of squaring and smoothing the surface around hole),
lapping (operation of sizing hardened holes and extremely limited in stock
removal), honing (The operation of finishing large holes such as automobile
cylinders by means of slow moving abrasives)
60.Grinding ratio =
61. Grinding wheel designation
62. Abrasive material used in grinding wheel for ferrous alloys  Al2O3.
63. Broaching cutting tool  Multipoint cutting tool
64. Surface roughness vs. machining; Surface roughness in machining can be
reduced by decreasing feed per revolution.
65. Machinability vs. alloying elements (like role of sulphur)
66. Machine tool beds material  grey cast iron
67. Shaping machine tool feed mechanism  Ratchet and Pawl Mechanism

39. 68. Build Up Edge (BUE) formation  Machining ductile materials at low speed 
Size of BUE increases with large uncut chip thickness
69. BUE formation can be avoided by using high cutting speed. BUE formation
results in tool life improvement.
70. Essential property for cutting tool  Hot hardness
71. In HSS tool, Tungsten can be replaced by Molybdenum.
72. Binding material used in cemented carbide cutting tool  Cobalt
73. Chip formation  Continuous chips (Ductile material); Discontinuous chips
(Brittle material)
74. Tool life calculation VTn
= C; where V  cutting speed in m/min; T  tool life; n 
exponent
75. Cutting tool materials (HSS, Diamond, CBN, Carbides)
76. Chip thickness ratio =
77. Chip thickness after cut always greater than before, so chip ratio always less
than 1.
78. Abrasive jet machining  Abrasive particles remove the material by micro
cutting action as well as brittle fracture
79. EDM  Used for hard metals which electrically conductive;
80. ECM  Electrolytic material removal process involving a negatively charged
shaped electrode (cathode), a conductive fluid (electrolyte), and a conductive
work piece (anode)
81. In Wire EDM (electro thermal machining process), wire material  brass
82. Cutting force in sheet metal operations (punching & blanking) mainly depends
on shear strength of the material.
83. For punching operation clearance is provided for the die, for blanking operation
clearance is provided for the punch.

40. 84. Metal forming – hot working (Above recrystallization temperature), cold
working (Below recrystallization temperature)
85. Allowance  Maximum clearance between the shaft and hole
86. 20G7f8  letter G indicates the position of the tolerance of the hole; H7-s6 
force fit (Interference fit)
87. Types of fits and applications
Clearance fit
88. Transition fit
89. Interference fit

41. 90. Angular measurement
Line standard angular measuring devices  Protractors, universal bevel
protractors
Face standard angular measuring devices  Sine bar, Sine center
Measurement of inclines  Spirit level, Clinometer
Angle comparators  Auto collimators
91. Surface roughness parameters:
Ra Arithmetic mean deviation of roughness profile
Rq  Root mean square deviation of roughness profile
Rz Maximum height of roughness profile
Rt Total height of roughness profile
Rv Maximum valley depth of roughness profile
Rp  Maximum peak height of roughness profile
Rsk  Skewness of the roughness profile
Rku  Kurtosis of the roughness profile
92. CNC, G - codes and M – codes
G01  Linear movement; G02  Clockwise circular movement; G03 Counter
clockwise circular movement; G04  Dwell period; G05  Hold; G81 
Drilling; G78 or 79  Milling; G85  Reaming; G86  Boring.
93. M00  Program stop; M01  Optional stop; M02  End of the program; M03
 Clockwise spindle rotation; M04  Counter clockwise spindle rotation; M05
 Spindle off; M06  Tool change; M07 or 08 Coolant ON; M09  Coolant
OFF;
94. Relation between strength and ductility
Strength α
95. Isotropy – Same properties in all directions, Anisotropy – Properties are not
same in all directions, Orthotropic – Properties differ at an angle of 90°

42. 96. Anisotropy in rolled plate material is caused by grain orientation.
97. In a wire drawing operation work material should possess ductility.
98. In rolling operation, the state of stress of the material undergoing deformation is
compression and shear.
99. Relationship between true strain and Engineering strain
ɛT = ln (1 + ɛE)
100. Mechanical properties
Strength  ability to resist external forces
Stiffness  ability to resist deformation under stress
Elasticity  property to regain its original shape
Plasticity  property which retains the deformation produced under load after
removing load
Ductility  property of a material to be drawn into wire form with using tensile
force
Brittleness  property of breaking a material without any deformation
Malleability  property of a material to be rolled or hammered into thin sheets
Toughness  property to resist fracture under impact load
Machinability  property of a material to be cut
Resilience  property of a material to absorb energy
Creep  material undergoes slow and permanent deformation when subjected
to constant stress with high temperature
Fatigue  failure of material due to cyclic loading
Hardness  resistant to indentation, scratch