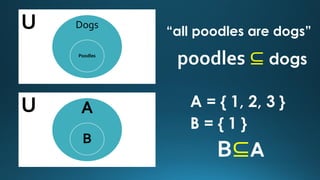
The document covers concepts related to universal sets, subsets, and proper subsets using Venn diagrams. It illustrates how to form sets from given elements and explains subset notation and relationships. Additionally, it includes exercises on identifying subsets and counting the number of subsets for different sets.

1. Grade 7 – Mathematics
Quarter I
UNIVERSAL SET
SUBSETS and VENN DIAGRAM

2. •define universal set, subset and
proper subset;
•illustrate subset and universal set
using Venn Diagram; and
•list all the possible subsets of a given
set;

3. Consider these cards.
Form the following sets using the numbers in the
cards.
1. A = {numbers less than 5}
A = {1,2,3,4}
2. B = {even numbers less than 5}
B = {2,4}

4. Consider these cards.
3. C = {prime numbers} C = {2,3,5,7}
4. D = {odd numbers} D = {1,3,5,7,9}
5. E = {numbers from 1 to 4} E = {1,2,3,4}

5. - denoted by U, contains all the
elements.
U = {1,2,3,4,5,6,7,8,9,10}

6. U = {1,2,3,4,5,6,7,8,9,10}
A = {1,2,3,4}
B = {2,4}
C = {2,3,5,7}
D = {1,3,5,7,9}
E = {1,2,3,4}

7. Subset
U
Venn Diagram

8. Dogs
Poodles
U “all poodles are dogs”
B⊆A
A
B
U A = { 1, 2, 3 }
B = { 1 }
poodles ⊆ dogs

9. - denoted by ⊆, if and only if every
element of set A is also an element of
set B.
- an empty set is always a subset of
every set.

10. - denoted by ⊂, if and only if every
element of set A is also an element
of set B, and set B contains at least
one element that is not in A.
- a proper subset is always a subset.

11. Example.
{3} _____ {1,2,3}⊂
{1,2,3} ___ {1,2,3}⊆
2 ___ {1,2,3}∈
5 ___ {1,2,3}∉
{7, 8} ___ {1,2,3}⊂
Proper Subset
Subset
Not a Subset
Element
Not an element

12. Let’s Try!
Fill in each blank with ⊂, ⊆, ∈, ∉, ⊂.
1. {2} _____ {1,2,3}
2. {g} _____ {a,b,c,d,e}
3. 4 _____ {odd number}
4. {3,2,1} _____ {1,2,3}
5. 1 _____ {1,2,3}
⊆
⊂
∉
⊂
∈

13. NUMBER OF SUBSETS
2. {1,2,3}
{ }
{1}, {2}, {3}
{1,2}, {2,3}, {1,3}
{1,2,3}
8 subsets
1. {a,b}
{ }
{a}, {b}
{a,b}
4 subsets

14. 3. {l,o,v,e}
{ }
{l}, {o}, {v}, {e}
{l,o}, {l,v}, {l,e}, {o,v}, {o,e}, {v,e}
{l,o,v}, {l,o,e}, {l,v,e}, {o,v,e}
{l,o,v,e}
16 subsets

15. Checking.
𝟐 𝒏
= 𝟐 𝒏𝒖𝒎𝒃𝒆𝒓 𝒐𝒇 𝒆𝒍𝒆𝒎𝒆𝒏𝒕𝒔
1. {a,b} = 4 subsets
𝟐 𝒏
= 𝟐 𝟐
= 2 x 2
2. {1,2,3} = 8 subsets
3. {l,o,v,e} = 16 subsets
𝟐 𝟑
= 𝟐 𝟑
= 2 x 2 x 2
𝟐 𝟒
= 𝟐 𝟒
= 2 x 2 x 2 x 2