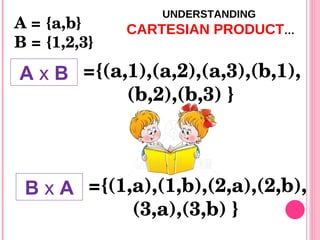
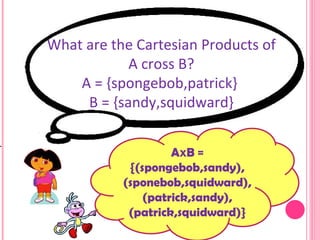
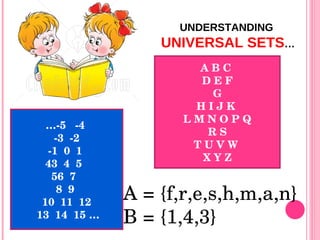
The document defines and provides examples of different set operations: 1) Universal sets are sets that contain all other sets as subsets. The universal set of countries would be all countries. 2) Complements of a set are elements that are in the universal set but not in the given set. The complement of letters in "crush" would be other letters. 3) Unions of sets contain all unique elements of the sets combined. The union of sets {1,2,3} and {2,4} is {1,2,3,4}. 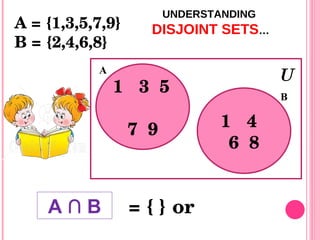4) Intersections of sets contain only elements common to both sets. The intersection of sets {1,2,3} and {

1. OPERATIONS ON SETS by: Teacher MYRA CONCEPCION

2. UNDERSTANDING UNIVERSAL SETS … A B C D E F G H I J K L M N O P Q R S T U V W X Y Z … -5 -4 -3 -2 -1 0 1 3 4 5 6 7 8 9 10 11 12 13 14 15 … A = {f,r,e,s,h,m,a,n} B = {1,4,3}

3. UNIVERSAL SET is where all the sets belong. In other words, all sets are a subset of Universal Set. REMEMBER: U is the symbol for universal set !

4. If a set consists of elements such as Philippines, Korea, United States and France , what could be the universal set? The universal set is consist of COUNTRIES!

5. UNDERSTANDING COMPLEMENTS OF A SET … c r u s h U A A = {c,r,u,s,h} or A = {x|x is a letter in the word “crush”} A’ ={a,b,d,e,f,g,i,j,k,l,m,n,o,p,q,t,v,w,x,y,z}

6. COMPLEMENT OF A SET is a set of elements that can be found in U but not in a certain set. It is denoted by ’ . In other words, complements of a set are elements that are OUT OF PLACE! FYI: There is another symbol for complement of a set!

7. If a set consists of letters in the sentence “ The quick brown fox jumps over the lazy dog.” , what could be its complement to U ? There will be no complement! The sentence consists all the letters of the English alphabet.

8. UNDERSTANDING COMPLEMENTS OF A SET … A = {1,2,4,5,7} B = {1,3,5,6} A – B The complement of B with respect to A. = {2,4,7} B – A The complement of A with respect to B. = {3,6}

9. What is F – B if F = {t,e,a,c,h} and B = {m,a,t,h}? The complements of B with respect to F are elements e and c .

10. UNDERSTANDING UNION OF SETS … A = {1,2,3,4,5} B = {2,4,6,8} A U B U C = {1,2,3,4,5,6,8} C = {1,3,5,7,9} A U B = {1,2,3,4,5,6,7,8,9}

11. UNION OF SETS is the set containing all the elements found in the sets being compared. It is denoted by U . In other words, union of sets is simply combing the elements of the sets! REMEMBER: Do not duplicate or repeat elements! DISTINCT

12. What is the union of sets P and C if P = {d,o,w,n} and C = {l,o,a,d}? P U C = {d,o,w,n,l,a,}

13. UNDERSTANDING INTERSECTION OF SETS … 1 3 5 U A A = {1,2,3,4,5} or A = {x|x is a number from 1 to 5} B = {2,4,6,8} or B = {x|x is a positive one-digit number} A ∩ B 6 8 2 4 B = {2,4}

14. INTERSECTION OF SETS is the set of all subsets that belongs to the two sets being compared. It is denoted by ∩. In other words, intersection of sets are the common elements for both sets. REMEMBER: Element should be seen on both sets!

15. What is the intersection of sets A and I if A = {c,l,a,r,k,s,o,n} and I = {d,a,u,g,h,t,r,y}? A ∩ I = {a,r}

16. UNDERSTANDING DISJOINT SETS … 3 5 7 9 U A 4 6 8 A = {1,3,5,7,9} B = {2,4,6,8} = { } or  A ∩ B B

17. DISJOINT SETS are sets having null or empty intersection. In other words, disjoint sets are sets without common element. REMEMBER: No elements are the same!

18. Which of the sets are disjoint ? O = {u,s,h,e,r} M = {j,u,s,t,i,n} G = {l,a,d,y,g} O and G M and G

19. UNDERSTANDING CARTESIAN PRODUCT … A = {a,b} B = {1,2,3} ={(a,1),(a,2),(a,3),(b,1),(b,2),(b,3) } A x B ={(1,a),(1,b),(2,a),(2,b),(3,a),(3,b) } B x A

20. CARTESIAN PRODUCT is a set consisting of all the pairs of the elements of set A to set B. This is denoted by x. A x B is read as “A cross B” REMEMBER: Elements in Cartesian Product should be PAIRS!

21. What are the Cartesian Products of A cross B? A = {spongebob,patrick} B = {sandy,squidward} A x B = {(spongebob,sandy), (sponebob,squidward), (patrick,sandy), (patrick,squidward)}

22. WE DID IT! Hurray!