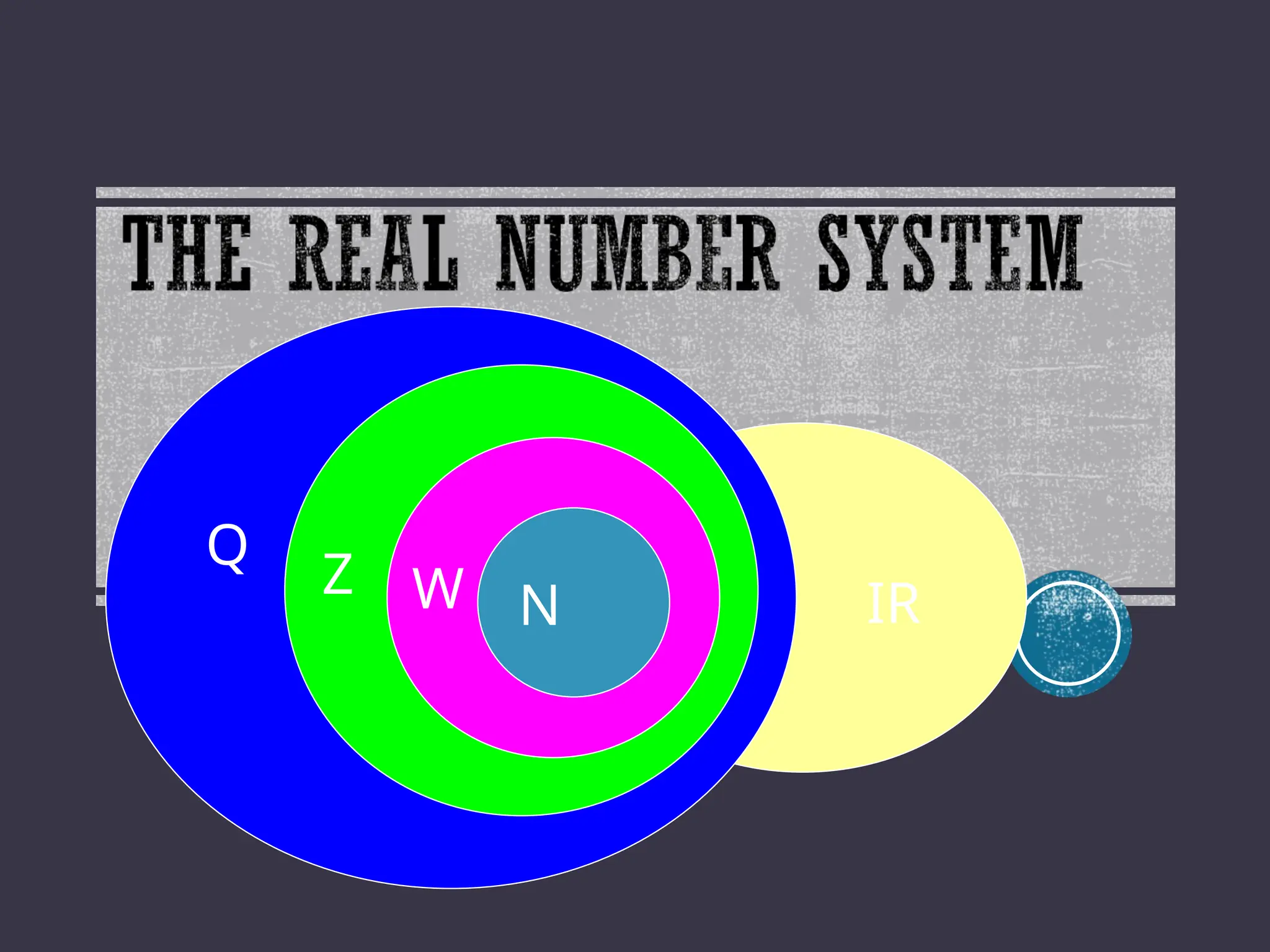
The document discusses the classification of numbers within the real number system, including rational and irrational numbers, as well as subsets like integers, whole numbers, and natural numbers. It defines rational numbers as those that can be expressed as fractions, while irrational numbers are characterized by non-terminating and non-repeating decimals. The text emphasizes understanding how to identify and differentiate between these number types.

1. N
W
Z
Q
IR

2. GOAL/OBJECTIVE
 Know that there are numbers that are not
rational and approximate them by rational
numbers.
 Understand informally that every number has a
decimal expansion; the rational numbers are
those with decimal expansions that terminate in
zeros or eventually repeat. Know that other
numbers are called irrational numbers.

3. ESSENTIAL QUESTION
How can you identify whether numbers are
rational or irrational, and where do they classify
within the number system?
N
W
Z
Q
IR

4. THE REAL NUMBER SYSTEM
 The Real Number System is made up of a set
of rational and irrational numbers.
 It has five subsets:
a. Rational Numbers (Q)
b. Integers (Z)
c. Whole Numbers (W)
d. Natural Numbers (N)
e. Irrational Numbers (IR)

5. WHAT ARE REAL NUMBERS?
 Real Numbers – consists of all rational and
irrational numbers.
 It includes any number that can be written as a
fraction, mixed numbers, terminating and
repeating decimals, whole numbers, integers,
square and cube roots.
4
1
2 3
5
4
1.5
2.3333 O
-6
2


6. WHAT ARE RATIONAL NUMBERS?
1
.5
2

.9
7.5
{…-3, -2, -1, 0, 1, 2, 3, …}
{…-3, -2, -1, 0, 1, 2, 3, …}
16 4

5
8 8.83333
6

• Rational Numbers – consists of integers,
terminating, and repeating decimals.
• It can also be expressed as a fraction, perfect
squares and perfect cubes.

7. WHAT ARE INTEGERS?
Integers – consist of natural numbers,
their opposites (negative #’s), and zero.
It does not include fractions or decimals.
All whole numbers are integers.
For example:
{…-3, -2, -1, 0, 1, 2, 3, …)}

8. WHAT ARE WHOLE AND NATURAL
NUMBERS?
Whole numbers – consist of
natural numbers and zero.
{0, 1, 2, 3, 4,…}
Natural numbers – are all the
counting numbers.
{1, 2, 3, 4…}

9. WHAT ARE TERMINATING AND REPEATING
DECIMALS?
Terminating Decimals are rational
numbers that stops before or after the
decimal point.
For example: 5.0, 2.75, .40, .0001…etc.
Repeating Decimals are rational numbers
that repeats after the decimal point.
For example: .3333…, ,
.75 10.635

10. WHAT ARE IRRATIONAL NUMBERS?
Irrational numbers consist of numbers that
are non-terminating and non-repeating
decimals.
They cannot be express as a fraction!
Pi is a great example of an irrational
number
pi
 
.001, .0011, .00111, .001111…etc
47 4.25837547984...
2

11. REAL NUMBER SYSTEM TREE
DIAGRAM
Real Numbers
Integers
Terminating
Decimals
Repeating
Decimals
Whole
Numbers
Rational Numbers
(Fractions & Perfect Squares/Cubes) Irrational Numbers
Negative #’s
Natural #’s Zero
Non-Terminating
And
Non-Repeating
Decimals

12. SUMMARY
What did you learn in this lesson?
What are some important facts to
remember about the real number
system?
Is there something within the
lesson that you need help on?

13. YOUR TURN
1.) How are the natural and whole numbers
different?
2.) How are the integers and rational numbers
different?
3.) How are the integers and rational numbers the
same?
4.) How are integers and whole numbers the same?
5.) Can a number be both rational and irrational?
Use the diagram to explain your answer.

14. Answer True or False to the statements below. If the
statement is False, explain why.
6.) 5 is a rational number. _______
−
7.) is rational. _______
8.) is a natural number __________
9.) is an integer. _______
10.) 2.434434443… is a rational number.____________
16
3.25

8
YOUR TURN