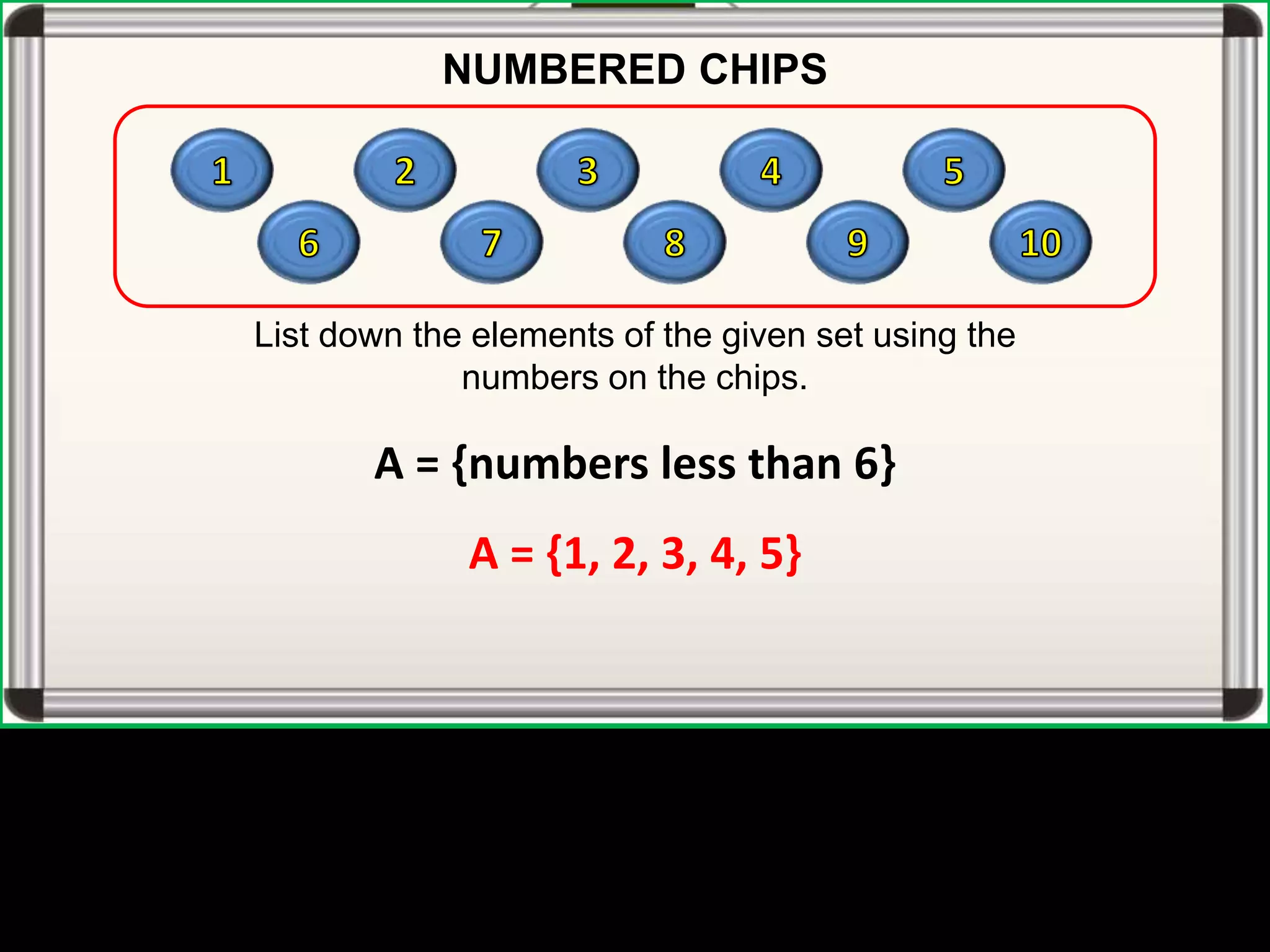
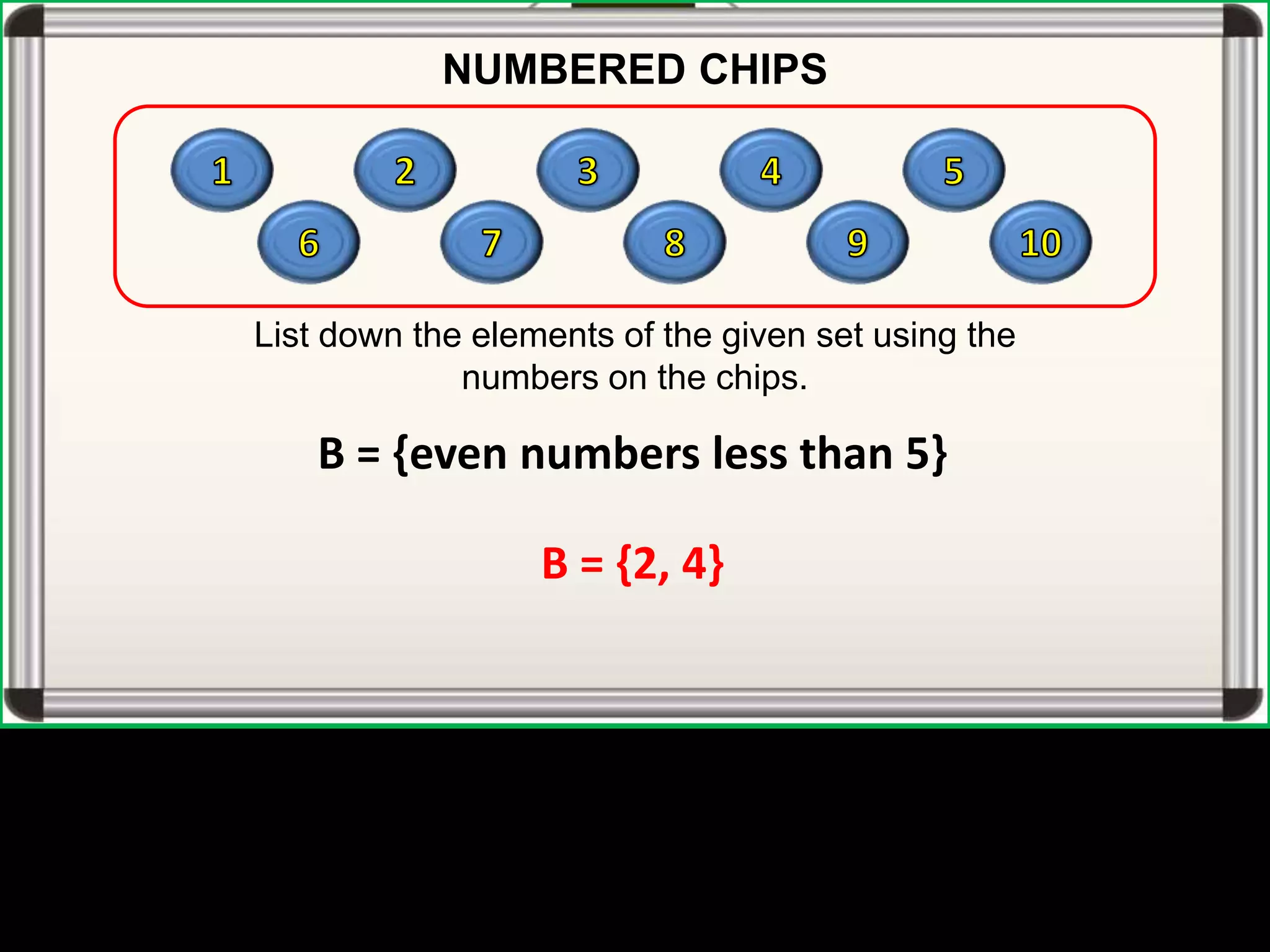
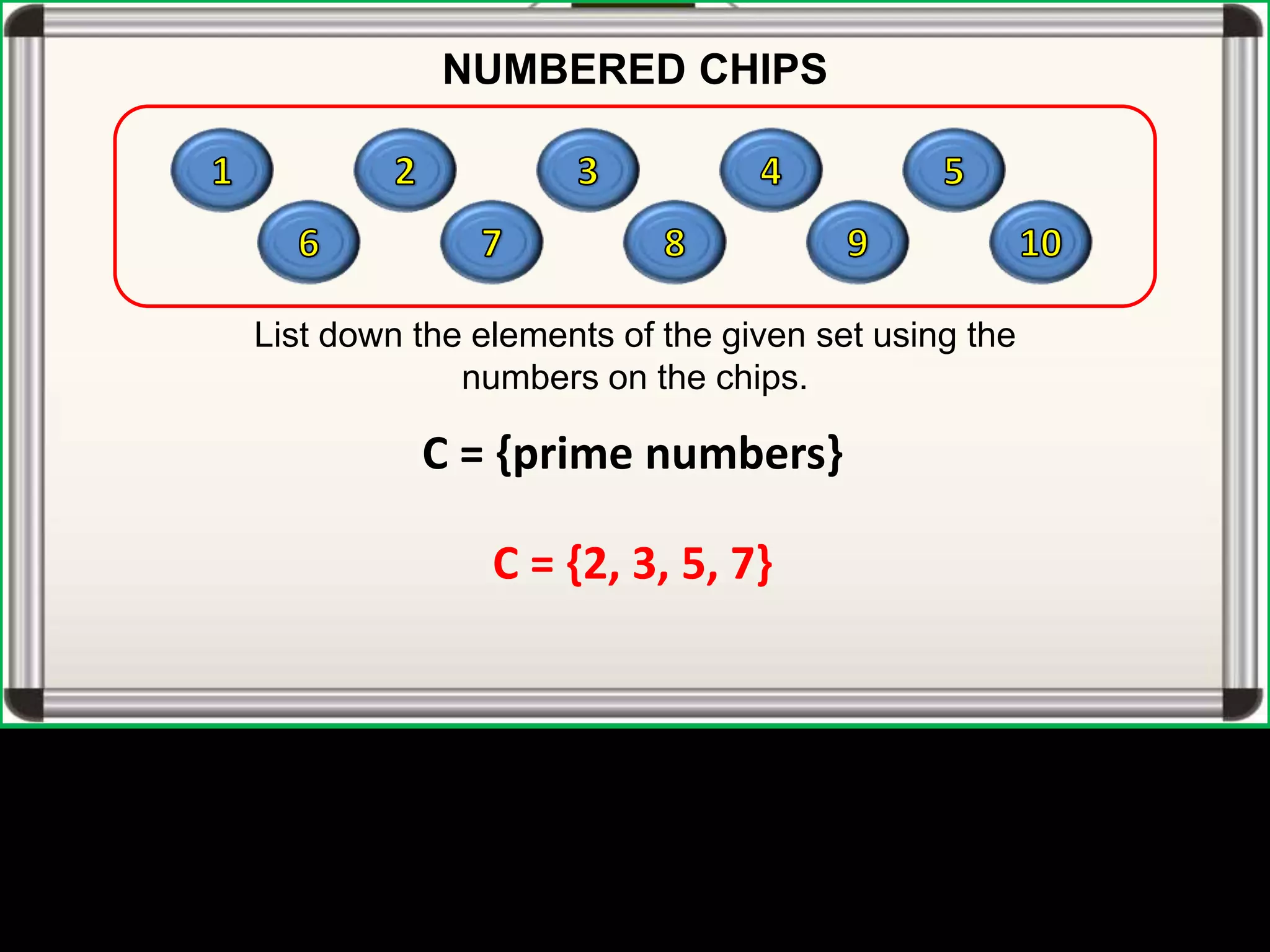
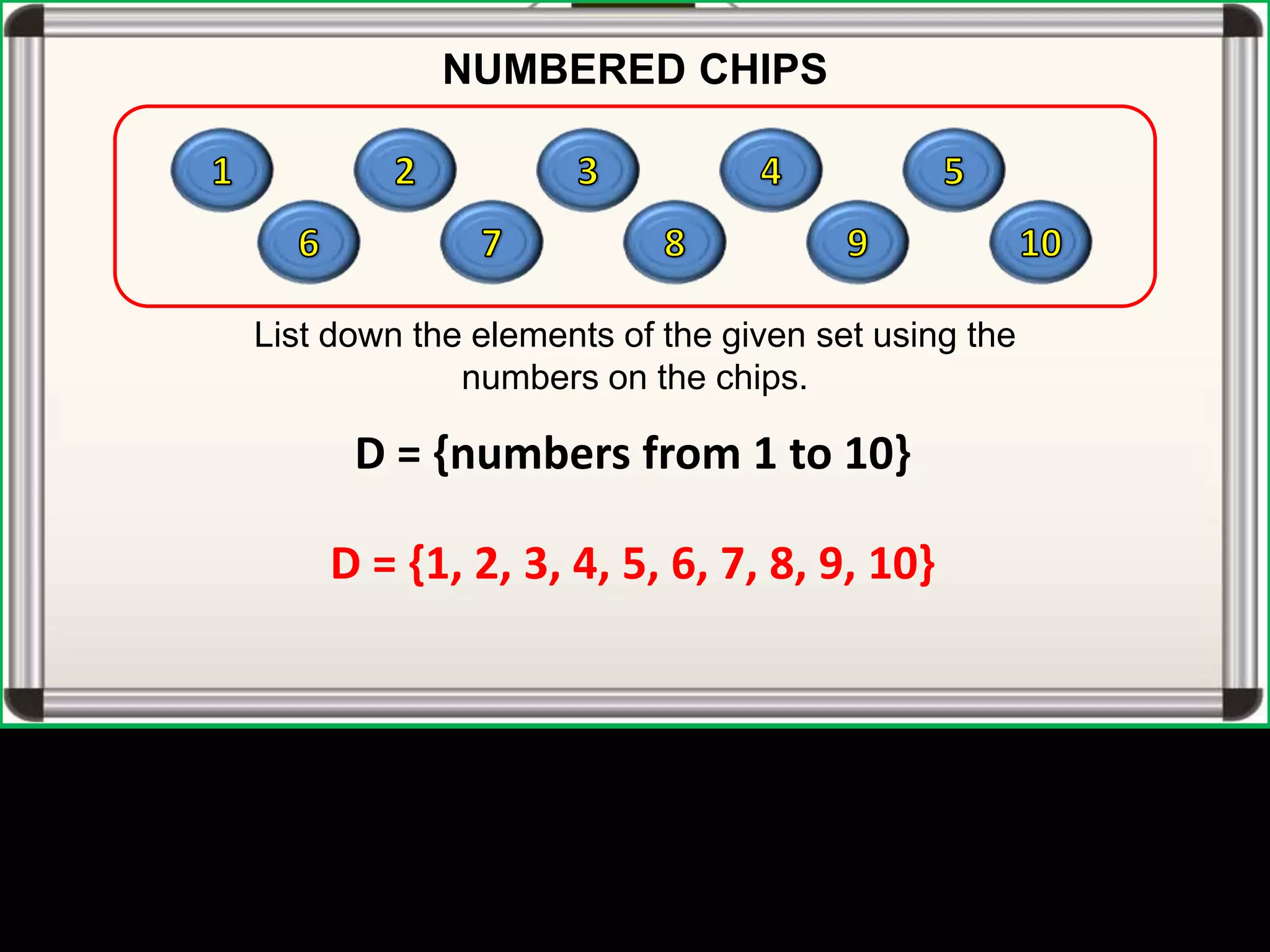
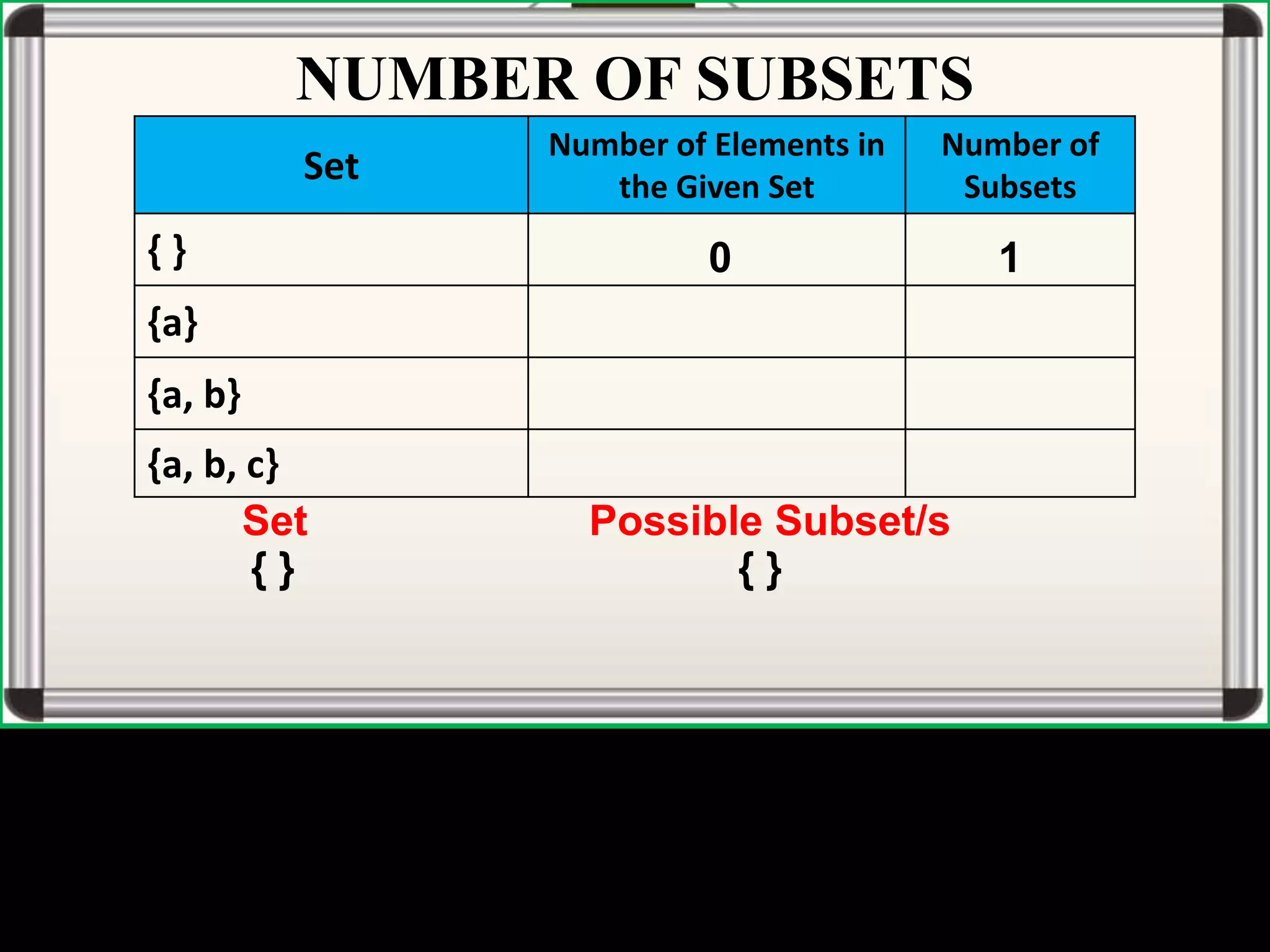
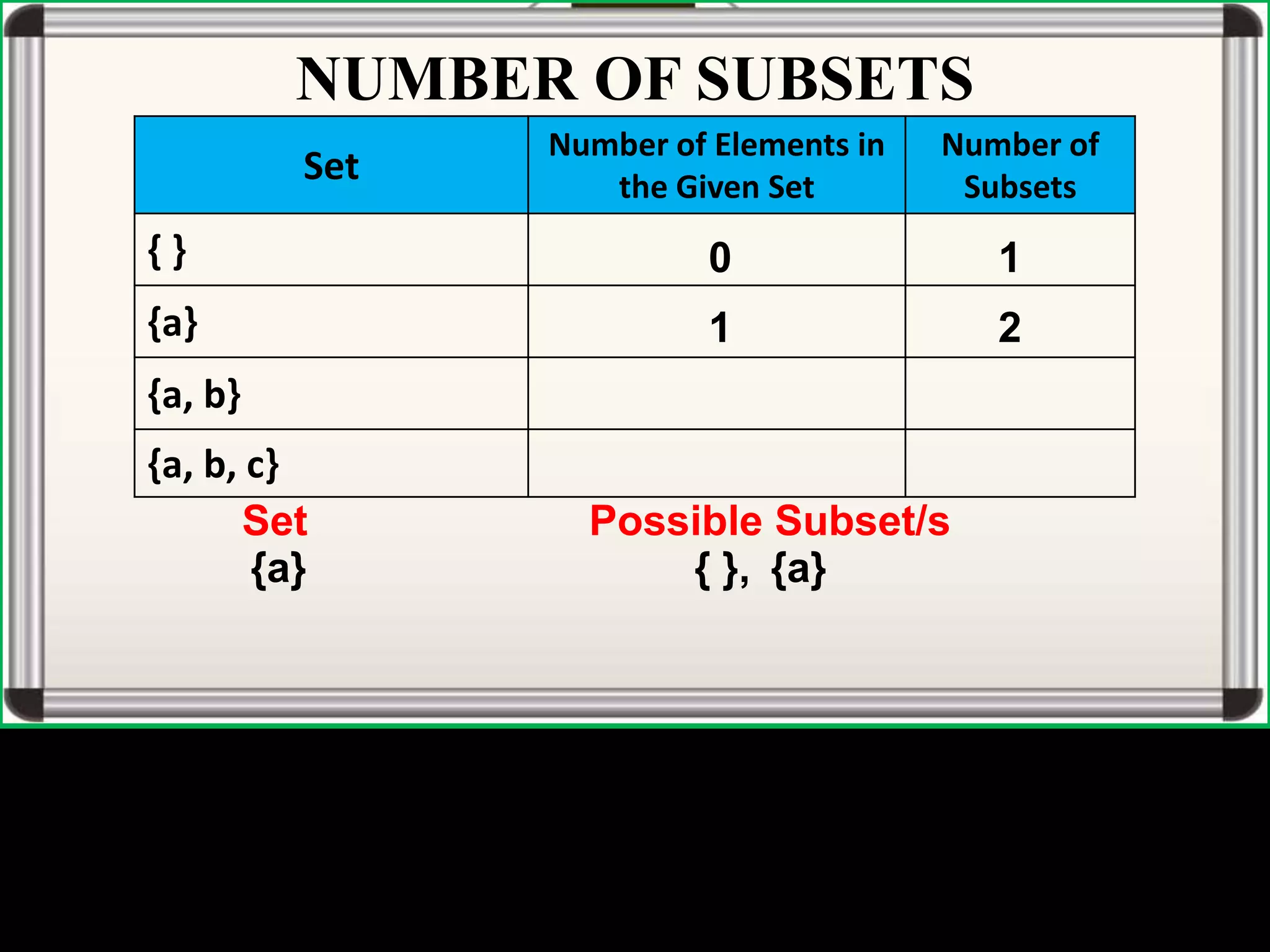
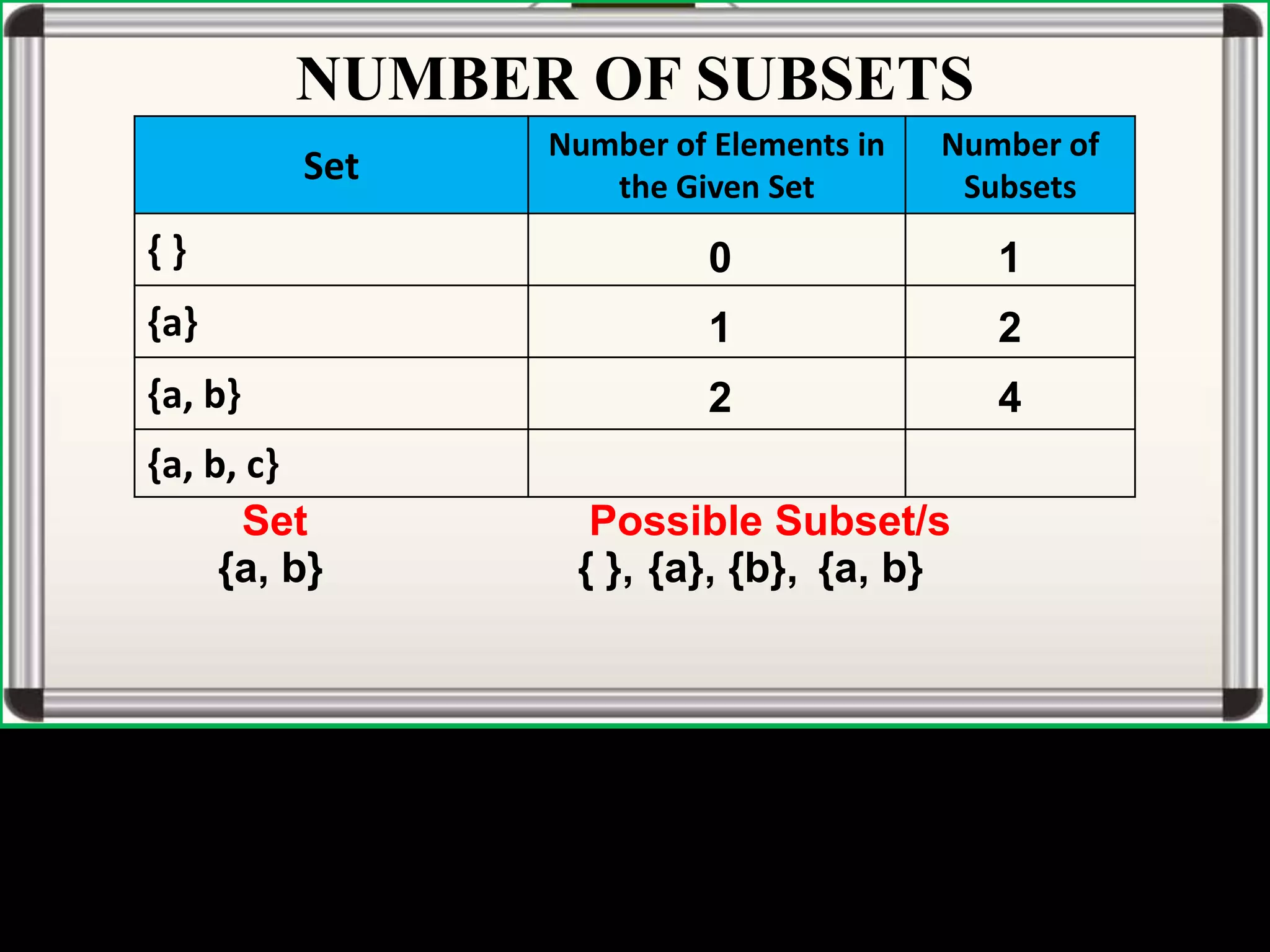
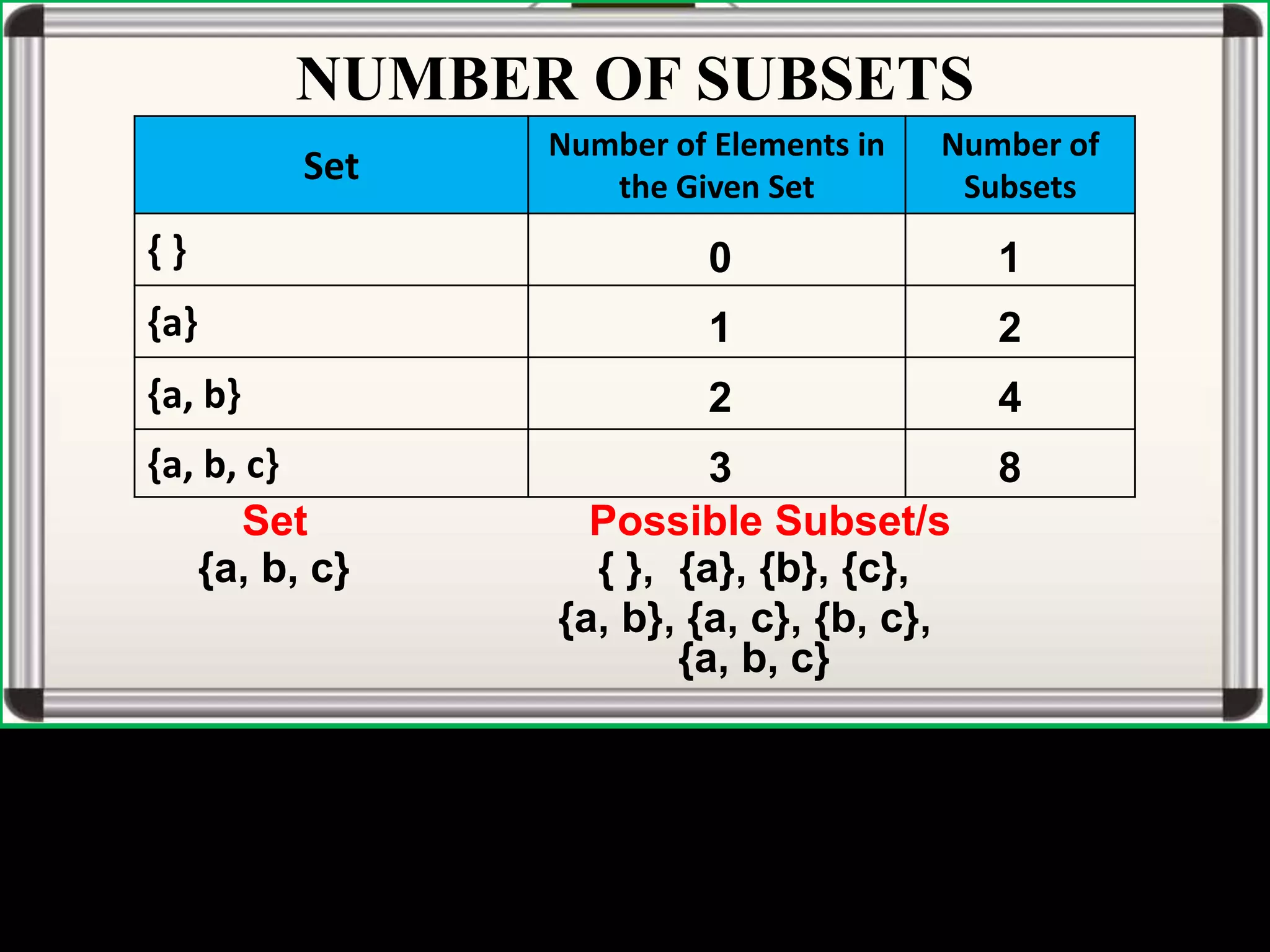
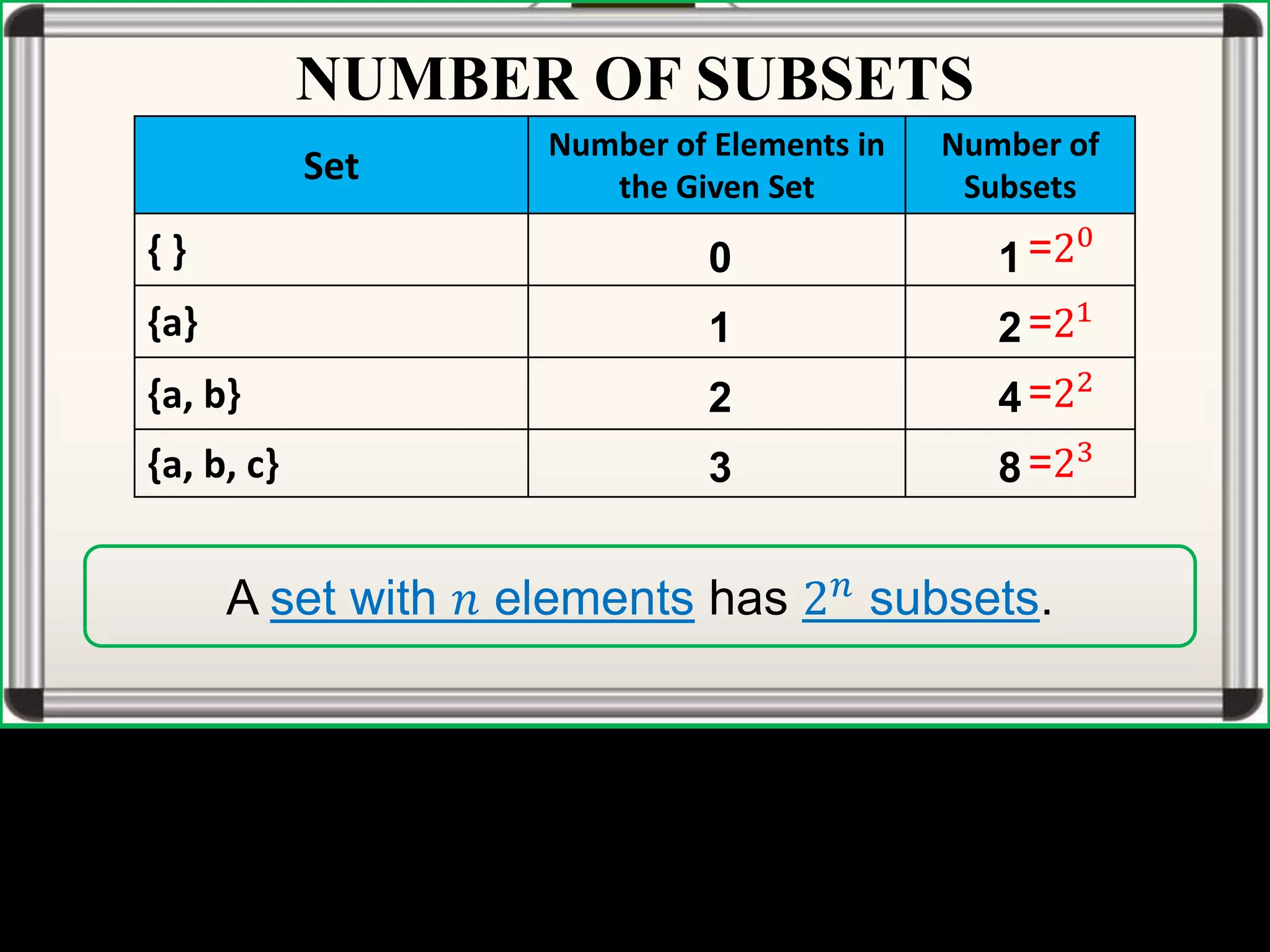
The document defines universal sets, subsets, and proper subsets. A universal set contains all elements being considered, while a subset contains elements that are also in the universal set. A proper subset is a subset where the universal set has at least one element not in the subset. The number of subsets of a set is equal to 2 to the power of the number of elements in the set.

1. UNIVERSAL SET
and
SUBSET

2. NUMBERED CHIPS
List down the elements of the given set using the
numbers on the chips.
A = {numbers less than 6}
A = {1, 2, 3, 4, 5}

3. B = {even numbers less than 5}
B = {2, 4}
NUMBERED CHIPS
List down the elements of the given set using the
numbers on the chips.

4. C = {prime numbers}
C = {2, 3, 5, 7}
NUMBERED CHIPS
List down the elements of the given set using the
numbers on the chips.

5. D = {numbers from 1 to 10}
D = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
NUMBERED CHIPS
List down the elements of the given set using the
numbers on the chips.

6. UNIVERSAL SET
The universal set, denoted by 𝑈, contains all
elements being considered in a given situation.
Example: (From the previous activity)
𝑼 = 𝟏, 𝟐, 𝟑, 𝟒, 𝟓, 𝟔, 𝟕, 𝟖, 𝟗, 𝟏𝟎 .

7. SUBSET
Set A is a subset of B, written as “𝐴 ⊆ 𝐵”, if and
only if every element of A is also an element of B.
REMEMBER!
A set is a subset of itself.
An empty set ( { } or ∅ } is a subset of any
given set!
Example: (From the previous activity)
𝑼 = 𝟏, 𝟐, 𝟑, 𝟒, 𝟓, 𝟔, 𝟕, 𝟖, 𝟗, 𝟏𝟎
A = {1, 2, 3, 4, 5} C = {2, 3, 5, 7}
B = {2, 4} D = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
We say,
𝑨 ⊆ 𝑼, 𝑩 ⊆ 𝑼, 𝑪 ⊆ 𝑼, and 𝑫 ⊆ 𝑼.
Also,
𝑩 ⊆ 𝑨, 𝑩 ⊆ 𝑫, and 𝑨 ⊆ 𝑫.
But,
𝑨 ⊈ 𝑩, and 𝑩 ⊈ 𝑪.

8. Set A is a proper subset of B, written as “𝐴 ⊂ 𝐵”, if and
only if:
1. A is a subset of B; and
2. B has at least one element that is not in A.
REMEMBER!
An empty set ( { } or ∅ } is a proper subset of
any set except of itself!
PROPER SUBSET
Example: (From the previous activity)
𝑼 = 𝟏, 𝟐, 𝟑, 𝟒, 𝟓, 𝟔, 𝟕, 𝟖, 𝟗, 𝟏𝟎
A = {1, 2, 3, 4, 5} C = {2, 3, 5, 7}
B = {2, 4} D = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
We say,
𝑨 ⊂ 𝑼, 𝑩 ⊂ 𝑼, and 𝑪 ⊂ 𝑼.
But,
𝑫 ⊄ 𝑼.

9. PRACTICE:
Tell whether the given set is a subset of
A = {1, 3, 5, 7, 9}. If it is a subset, specify if it is a proper
subset or not.
1. {3, 5} 3. {1, 3, 5, 7, 9}
2. { } 4. {2, 3}
Answers
1. subset (proper)
2. subset (proper)
3. subset (not proper)
4. not a subset

10. NUMBER OF SUBSETS
Set
Number of Elements in
the Given Set
Number of
Subsets
{ }
{a}
{a, b}
{a, b, c}
0
{ }
1
Set Possible Subset/s
{ }

11. Set
Number of Elements in
the Given Set
Number of
Subsets
{ }
{a}
{a, b}
{a, b, c}
0
1
{ },
1
2
Set Possible Subset/s
{a} {a}
NUMBER OF SUBSETS

12. Set
Number of Elements in
the Given Set
Number of
Subsets
{ }
{a}
{a, b}
{a, b, c}
0
1
2
1
2
4
{ },
Set Possible Subset/s
{a, b} {a}, {b}, {a, b}
NUMBER OF SUBSETS

13. Set
Number of Elements in
the Given Set
Number of
Subsets
{ }
{a}
{a, b}
{a, b, c}
0
1
2
1
2
4
3 8
{ },
Set Possible Subset/s
{a, b, c} {a}, {b}, {c},
{a, b}, {a, c}, {b, c},
{a, b, c}
NUMBER OF SUBSETS

14. Set
Number of Elements in
the Given Set
Number of
Subsets
{ }
{a}
{a, b}
{a, b, c}
0
1
2
1
2
4
3 8
=20
=21
=22
=23
A set with 𝑛 elements has 2𝑛 subsets.
NUMBER OF SUBSETS

15. PRACTICE:
Answer the following questions.
1. If a set has 4 elements, how many subsets does it have?
2. How many subsets does a set have if it has 7 elements?
3. If a set has 64 subsets, how many elements does it have?
Answers
1. 16 subsets
2. 128 subsets
3. 6 elements
Solution: 𝟐𝟕
= 𝟐 × 𝟐 × 𝟐 × 𝟐 × 𝟐 × 𝟐 × 𝟐 = 𝟏𝟐𝟖
Solution: 𝟔𝟒 = 𝟐 × 𝟐 × 𝟐 × 𝟐 × 𝟐 × 𝟐
2 was used as a factor 6 times
Solution: 𝟐𝟒 = 𝟐 × 𝟐 × 𝟐 × 𝟐 = 𝟏𝟔

16. Consider the set B = {1, 2, 3, 4, 5}.
Test Yourself!!!
1. List all its subsets.
2. How many subsets does it have?
3. How many proper subsets does it have?
Consider the set
A = {odd counting numbers less than 10}.
State whether the given statement is TRUE or FALSE.
1. {1, 5} ⊆ A 3. {1, 5, 9} ⊂ A 5. ∅ ⊈ A
2. {8, 9} ⊆ A 4. {1, 3, 5, 7, 9} ⊂ A