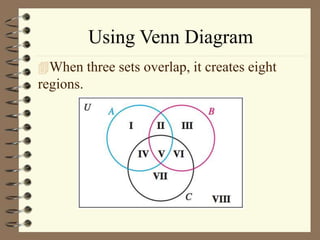
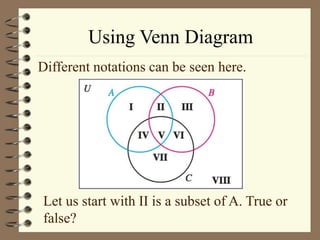
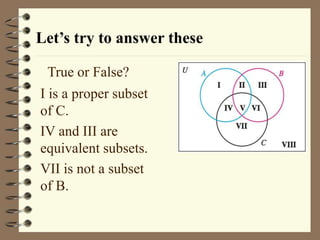
The document defines key terms related to sets and subsets, including: - A set A is a subset of set B if all elements of A are also elements of B. - A set A is a proper subset of B if A is a subset of B, but A does not contain all the same elements as B. - Two sets are equal if they contain all the same elements. It provides examples of determining if one set is a subset or proper subset of another set. Venn diagrams are introduced as a way to visualize the relationships between sets.

1. Subsets
Part I
Melanie B. Bargo

2. Where we’re going?
Let’s try to be able to:
Define subset, proper subset, and
equivalent sets.
Indicate that one set is a subset of
another by writing the proper notation.
Indicate that one set is not a subset of
another by writing the proper notation.

3. Where we’re going?
Let’s try to be able to:
Describe the procedure for drawing and
labeling a Venn diagram to show the
relationship between a set and its subset.
Identify the relationships between sets
and their subsets using a Venn diagram.
Define equivalent sets in terms of
subsets.

4. Where we’re going?
Let’s try to be able to:
List all subsets for a given set using
proper notation.
Recognize that the empty (null) set is a
subset of all sets.

5. Subsets
• Set A is a subset of set B,
symbolized A ⊆ B, if and only if
all elements of set A are also
elements of set B.
• The symbol A ⊆ B indicates that
“set A is a subset of set B.”

6. Subsets
• The symbol A ⊈ B set A is not a
subset of set B.
• To show that set A is not a
subset of set B, one must find
at least one element of set A
that is not an element of set B.

7. Determining Subsets
Example:
Determine whether set A is a
subset of set B.
A = { 3, 5, 6, 8 }
B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Solution:
All of the elements of set A are
contained in set B, so A ⊆ B.

8. Proper Subset
Set A is a proper subset of set B,
symbolized A ⊂ B, if and only if all of
the elements of set A are elements of set
B and set A ≠ B (that is, set B must
contain at least one element not is set A).

9. Determining Proper Subsets
Example:
Determine whether set A is a
proper subset of set B.
A = { dog, cat }
B = { dog, cat, bird, fish }
Solution:
All the elements of set A are
contained in set B, and sets A and
B are not equal, therefore A ⊂ B.

10. Determining Proper Subsets
Example:
Determine whether set A is a
proper subset of set B.
A = { dog, bird, fish, cat }
B = { dog, cat, bird, fish }
Solution:
All the elements of set A are
contained in set B, but sets A and
B are equal, therefore A ⊄ B.

11. Clarify Notation
If A is a subset of B we write
A  B to designate that relationship.
If A is a proper subset of B we write
A  B to designate that relationship.
If A is not a subset of B we write
A  B to designate that relationship.

12. Example - subset
The set A = {1, 2, 3} is a subset of the set B
={1, 2, 3, 4, 5, 6} because each element of
A is an element of B.
We write A  B to designate this relationship
between A and B.
We could also write
{1, 2, 3}  {1, 2, 3, 4, 5, 6}

13. Example - subset
The set A = {3, 5, 7} is not a subset of the
set B = {1, 4, 5, 7, 9} because 3 is an
element of A but is not an element of B.
The empty set is a subset of every set,
because every element of the empty set is
an element of every other set.

14. Example - subset
The set
A = {1, 2, 3, 4, 5} is a subset of the set
B = {x | x < 6 and x is a counting number}
because every element of A is an element
of B.
Notice also that B is a subset of A because every
element of B is an element of A.

15. August 2006 Copyright © 2006 by DrDelMath.Com
15
Equivalent Sets
Two sets A and B are equal
if A  B and B  A. If two
sets A and B are equal we
write A = B to designate that
relationship.

16. Example - equality
The sets
A = {3, 4, 6} and B = {6, 3, 4} are
equal because A  B and B  A.
The definition of equality of sets shows that the
order in which elements are written does not
affect the set.

17. Example - equality
The sets A = {2} and B = {2, 5} are not
equal because B is not a subset of A. We
would write A ≠ B. Note that A  B.
The sets A = {x | x is a fraction} and
B = {x | x = ¾} are not equal because A
is not a subset of B. We would write
A ≠ B. Note that B  A.

18. Using Venn Diagram
When three sets overlap, it creates eight
regions.
2.4-18

19. Using Venn Diagram
Different notations can be seen here.
2.4-19
Let us start with II is a subset of A. True or
false?

20. Let’s try to answer these
True or False?
I is a proper subset
of C.
IV and III are
equivalent subsets.
VII is not a subset
of B.

22. Thank you!