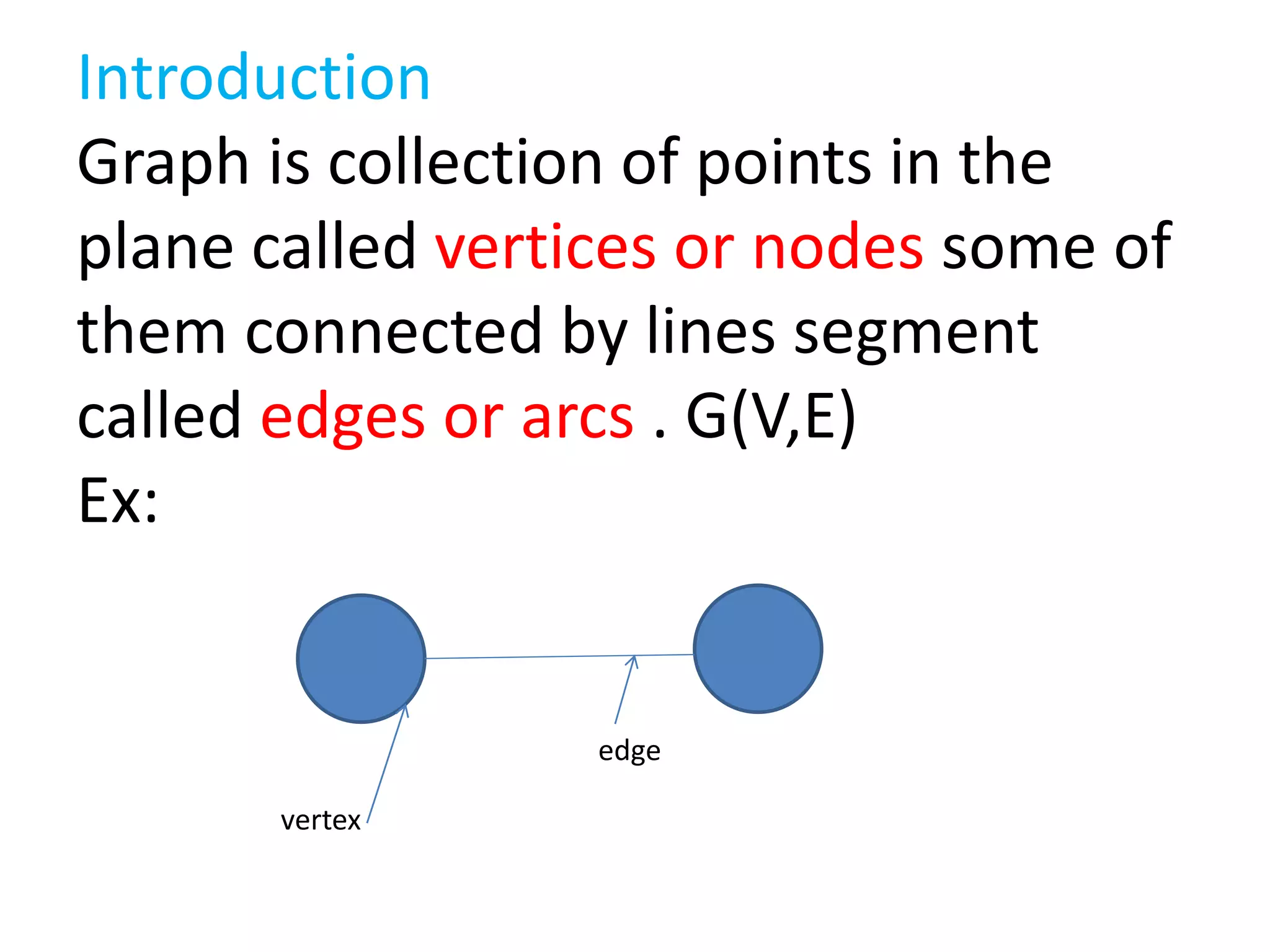
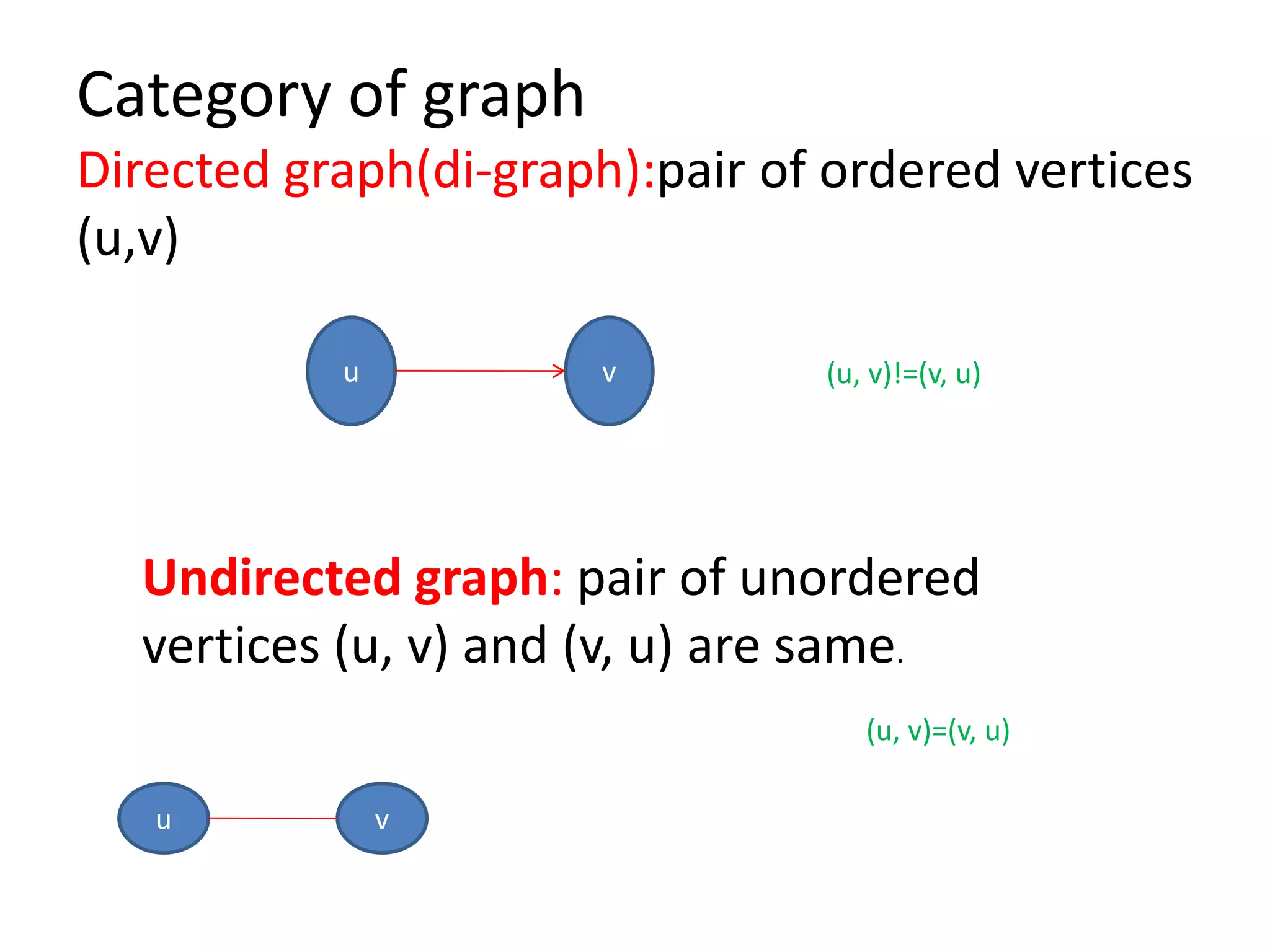
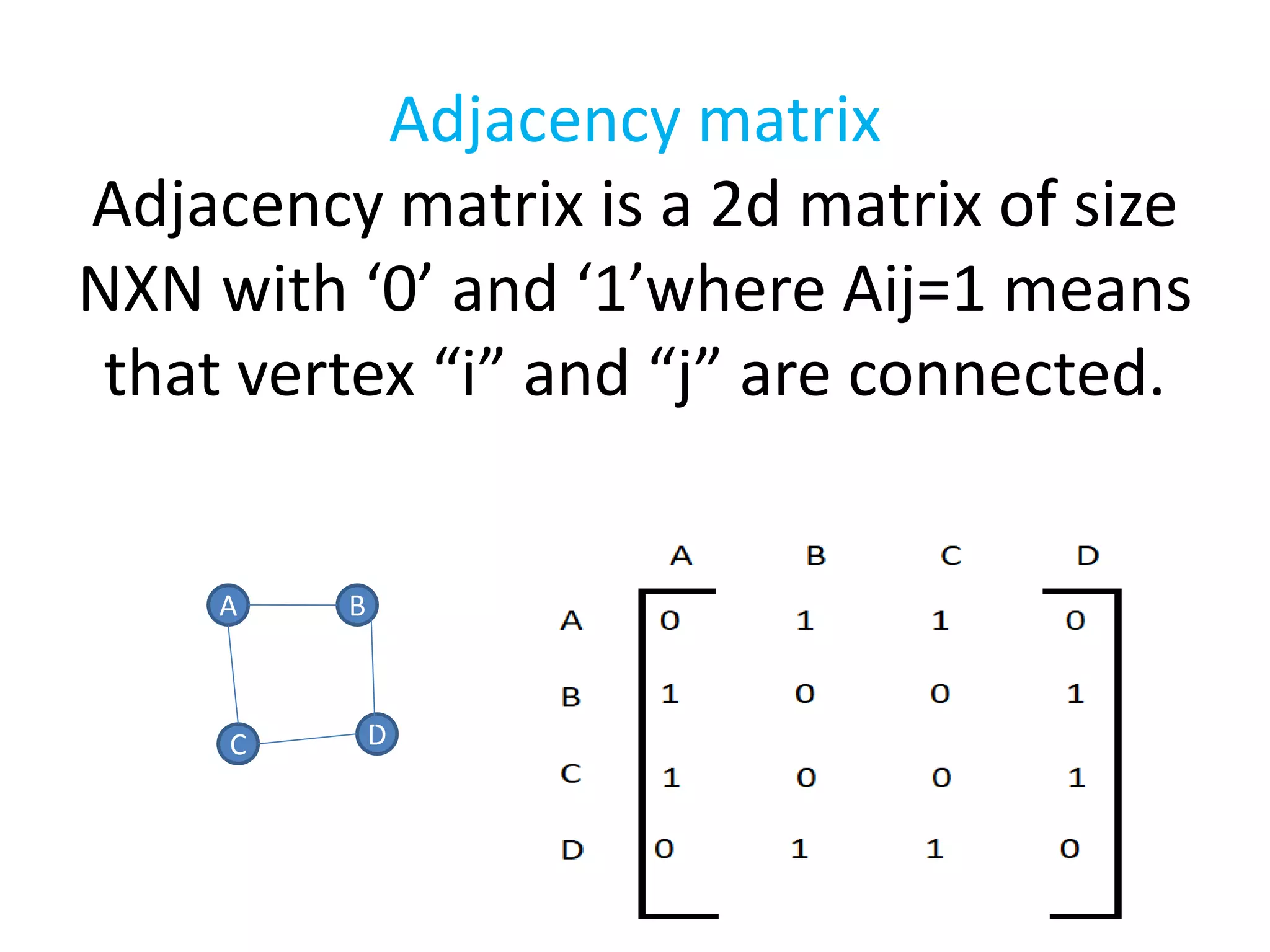
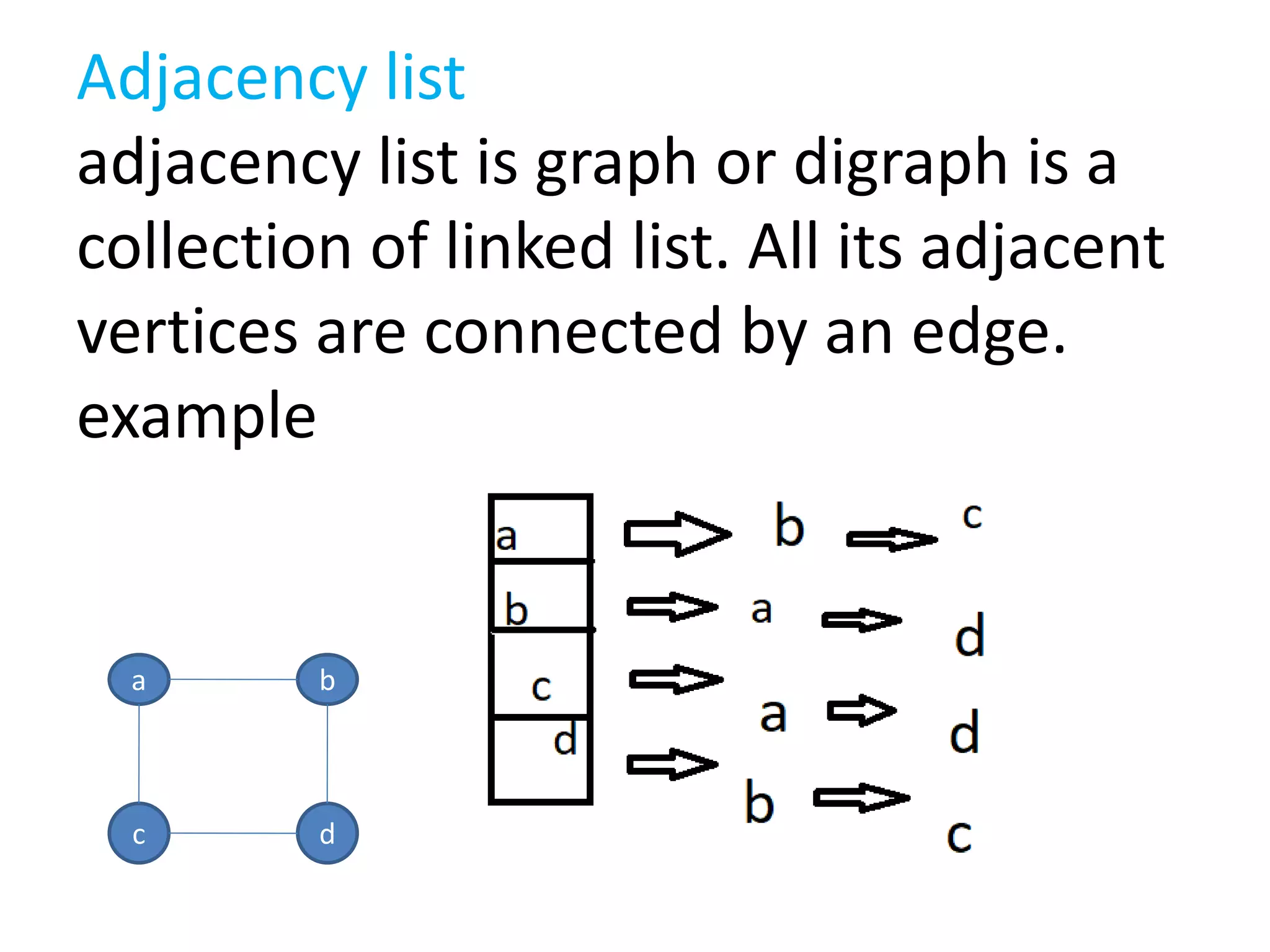
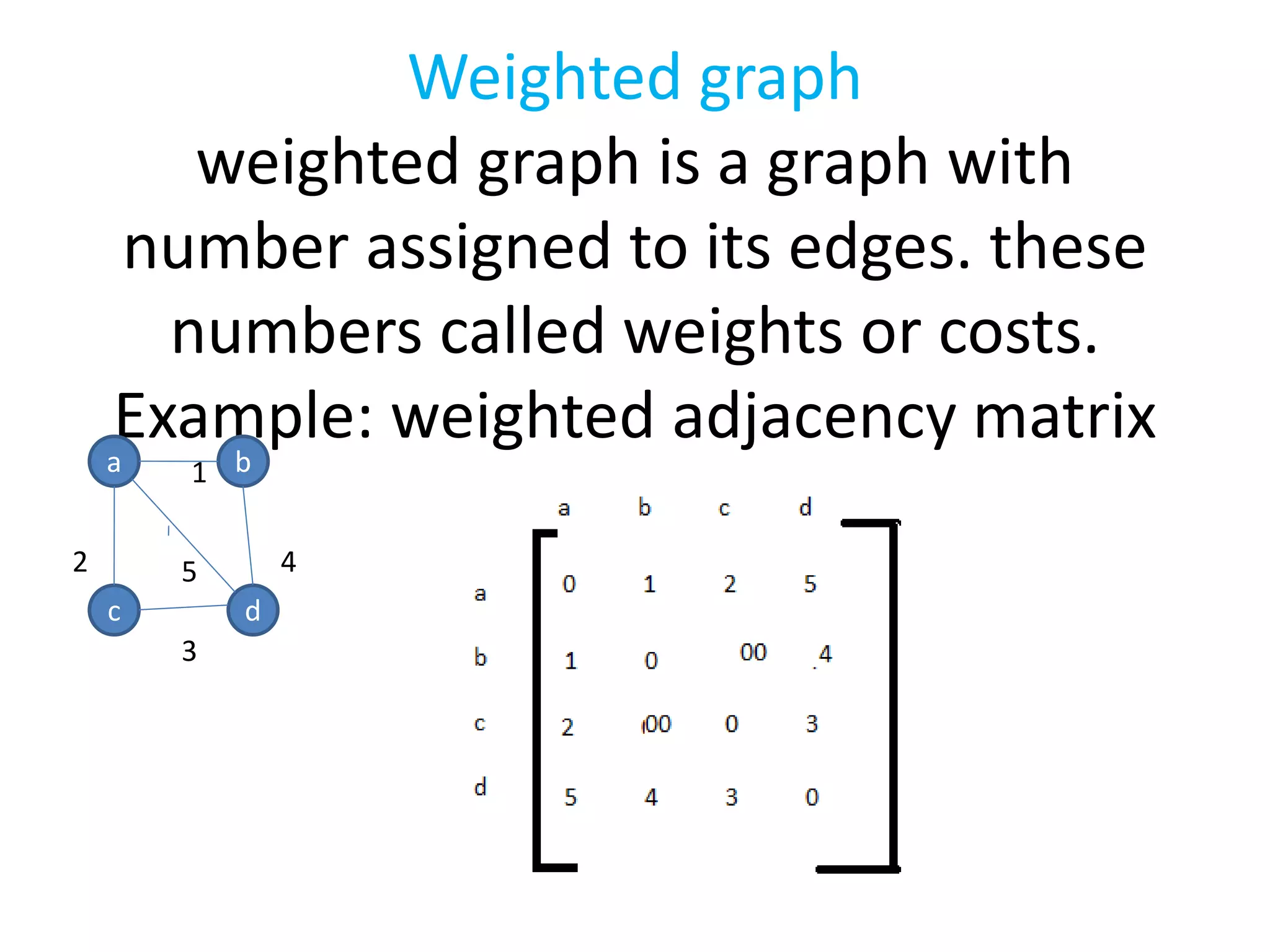
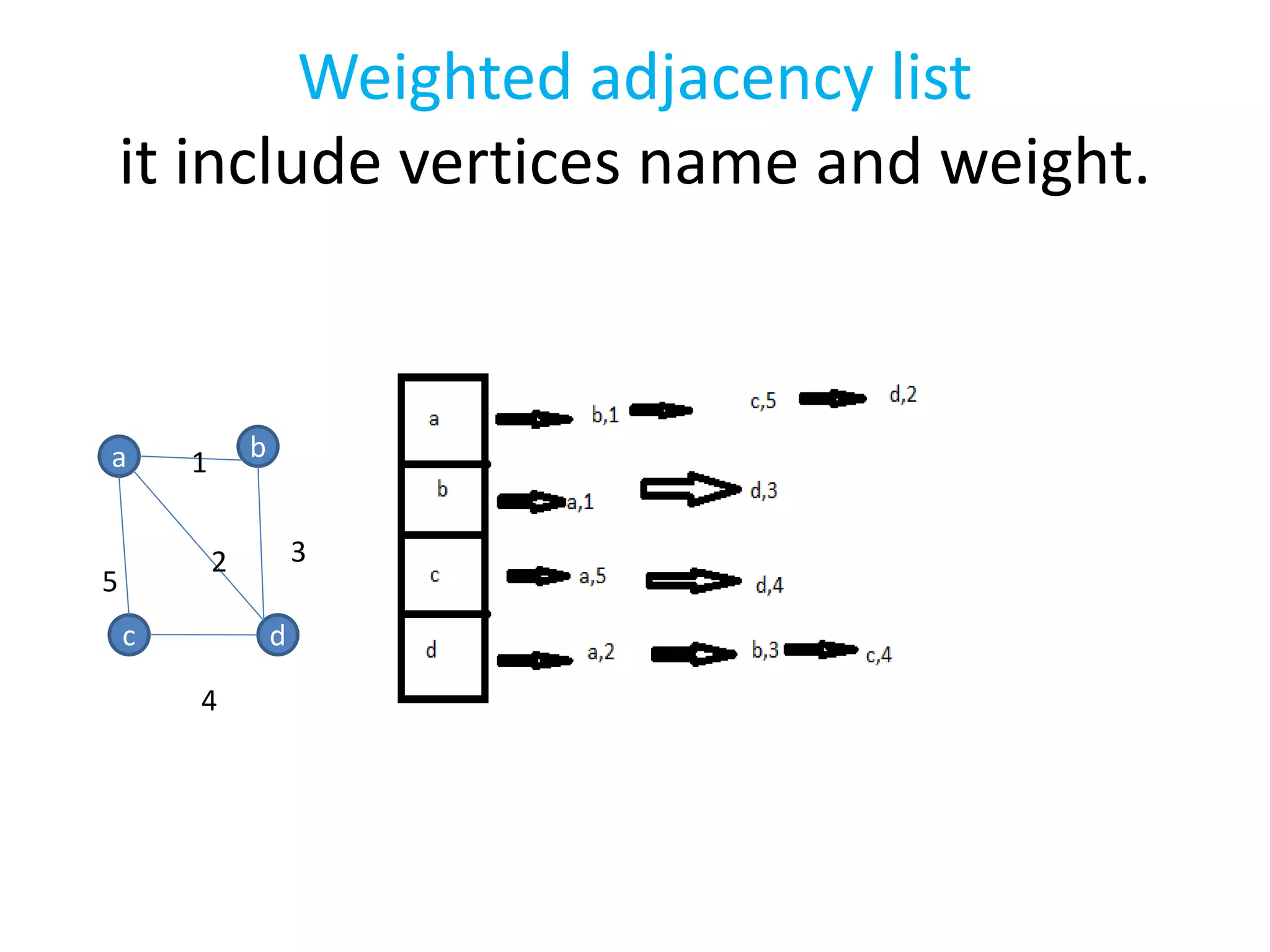
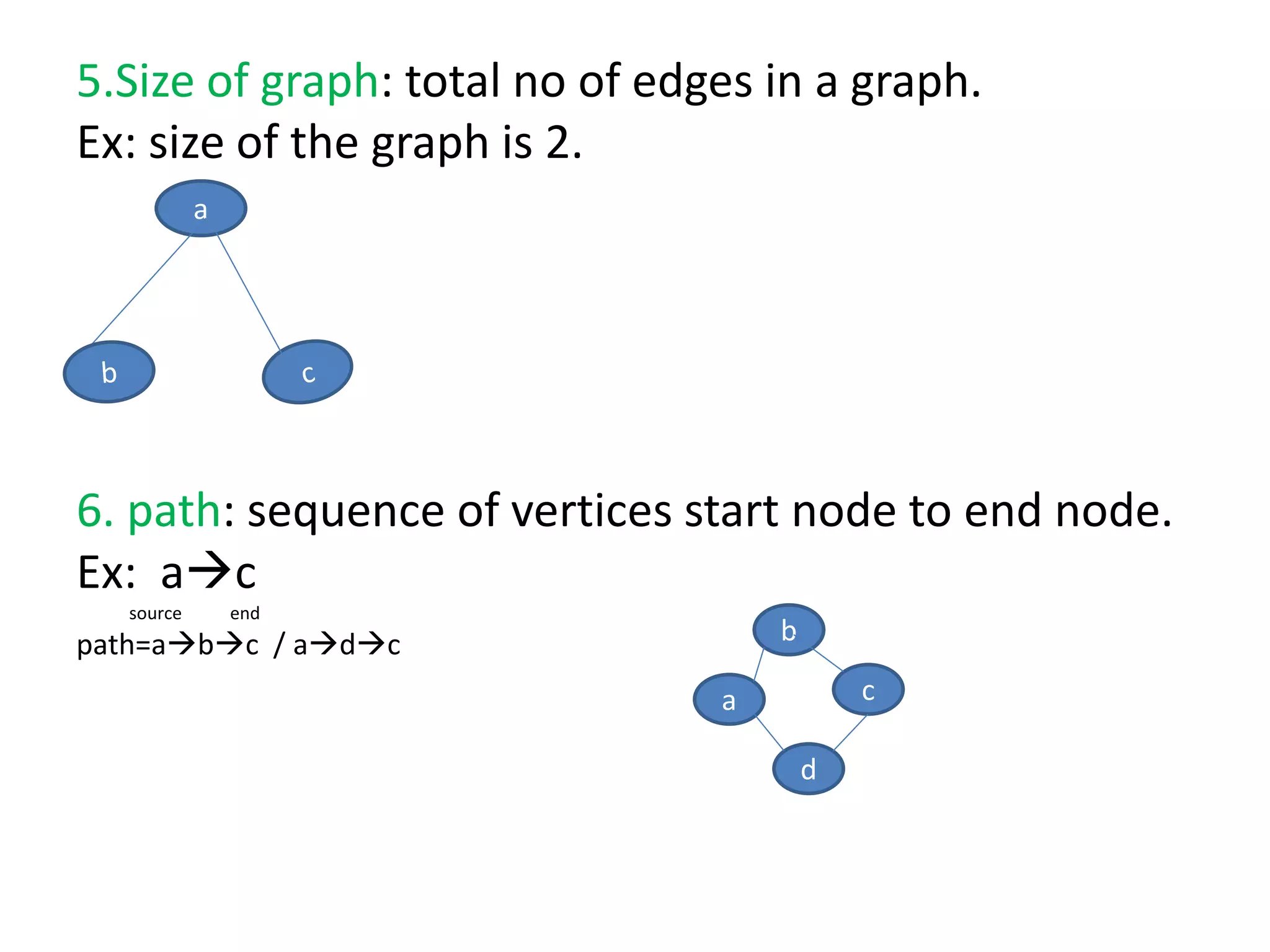
This document introduces graphs as collections of vertices connected by edges, detailing the difference between directed and undirected graphs. It further explains graph representations using adjacency matrices and lists, along with concepts of weighted graphs and various terminologies related to graphs such as nodes, edges, and cycles. Key examples illustrate the discussed concepts, providing clarity on graph structures and their properties.

1. GRAPH
Introduction and representation
By Bharati.C
M.tech

2. Introduction
Graph is collection of points in the
plane called vertices or nodes some of
them connected by lines segment
called edges or arcs . G(V,E)
Ex:
edge
vertex

3. Category of graph
Directed graph(di-graph):pair of ordered vertices
(u,v)
u v
Undirected graph: pair of unordered
vertices (u, v) and (v, u) are same.
(u, v)!=(v, u)
(u, v)=(v, u)
u v

4. Graph representation
There are generally two ways to
represent a graph data structure.
1. Adjacency matrix.
2. Adjacency list.

5. Adjacency matrix
Adjacency matrix is a 2d matrix of size
NXN with ‘0’ and ‘1’where Aij=1 means
that vertex “i” and “j” are connected.
A B
C D

6. Adjacency list
adjacency list is graph or digraph is a
collection of linked list. All its adjacent
vertices are connected by an edge.
example
a b
c d

7. Weighted graph
weighted graph is a graph with
number assigned to its edges. these
numbers called weights or costs.
Example: weighted adjacency matrix
a b
c d
1
2
3
4
5

8. Weighted adjacency list
it include vertices name and weight.
c
b
a
d
1
3
4
5
2

9. Graph Terminology

10. Graph terminology
1. node: In a plane collection of point called
vertex.
2. edge: connected a line segment to vertices.
3. adjacent node: which connect near vertices.
4. degree of nodes: no of edges connected to
that node.
Ex: degree of a=2 nodes
degree of b=1 nodes
a
b c

11. 5.Size of graph: total no of edges in a graph.
Ex: size of the graph is 2.
6. path: sequence of vertices start node to end node.
Ex: ac
source end
path=abc / adc
a
b
a c
d

12. 7. Path length: total weight of distance value
obtained by particular path start node to end
node.
Ex: a to d=1+2=3
8. connected graph: every vertices are
connected.
9. not connected graph: every vertices are not
connected.
Ex:
a
b
d
c
1
2
3
4
a
c
e
d
b

13. 10. cycle: a cycle is a path of a source to ends at
same vertex and does not traverse the same
edge more than once. Ex: a—b—c—a
11. acycle: a graph with no cycle is said to be
acycle.
a
b c