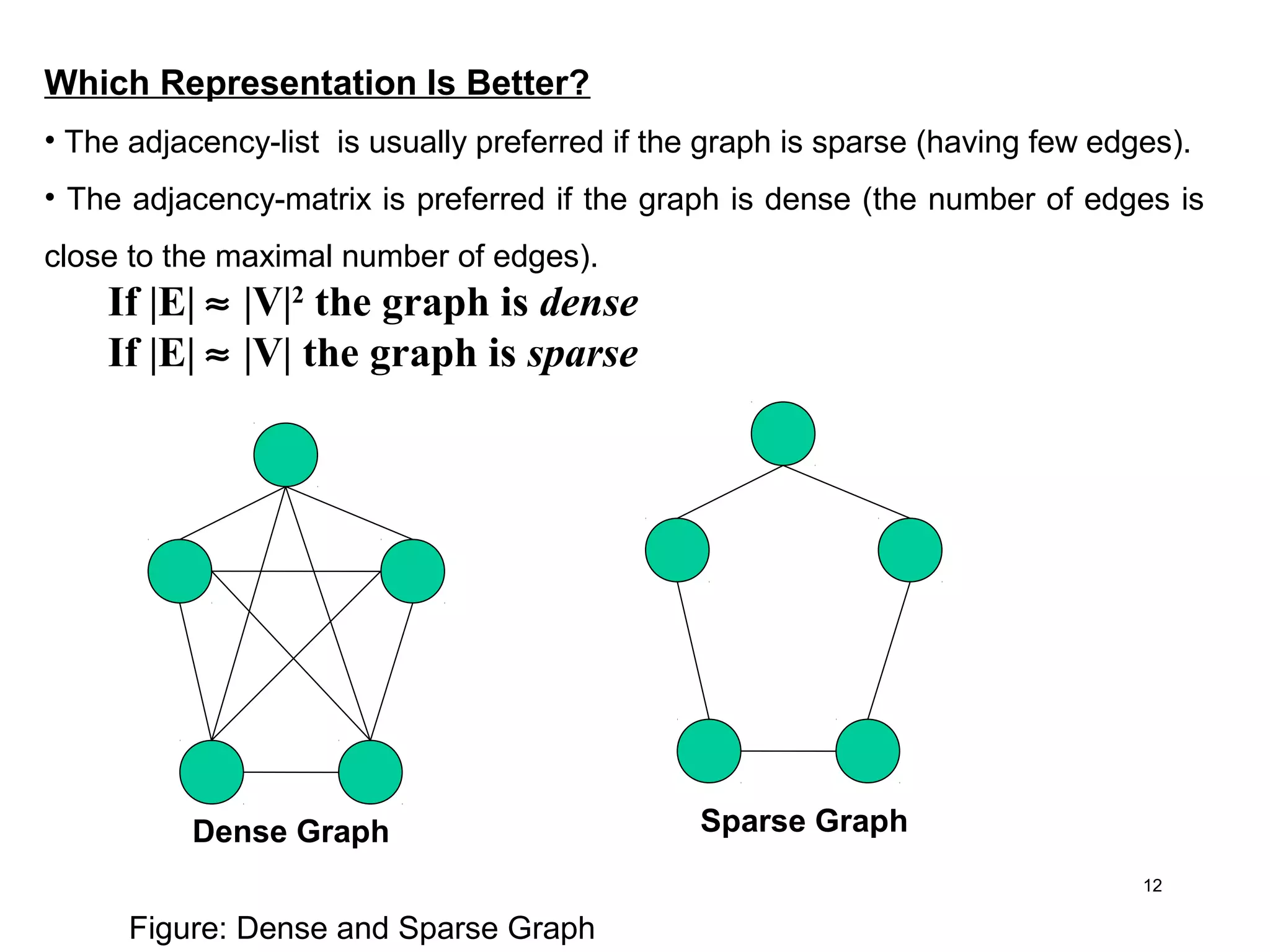
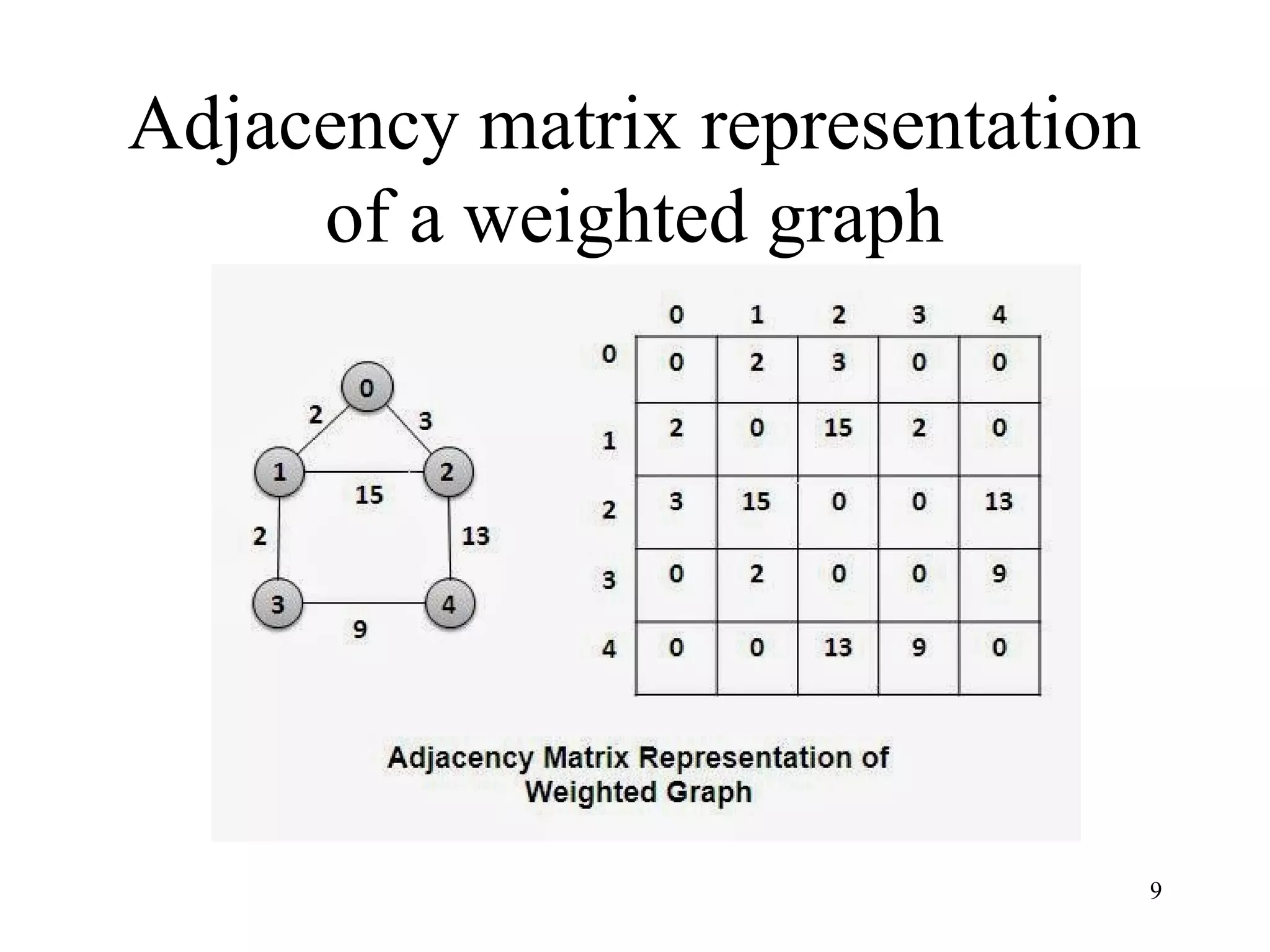
This document discusses graphs and their applications and representations. It defines what a graph is consisting of vertices and edges. It describes different types of graphs such as trees, connected graphs, weighted graphs, directed graphs, and multigraphs. It also discusses graph representations including adjacency matrices and adjacency lists. Finally, it notes that adjacency lists are generally preferred for sparse graphs while adjacency matrices are better for dense graphs.

1. Graph and Its Applications
1

2. • Nonlinear data Structures.
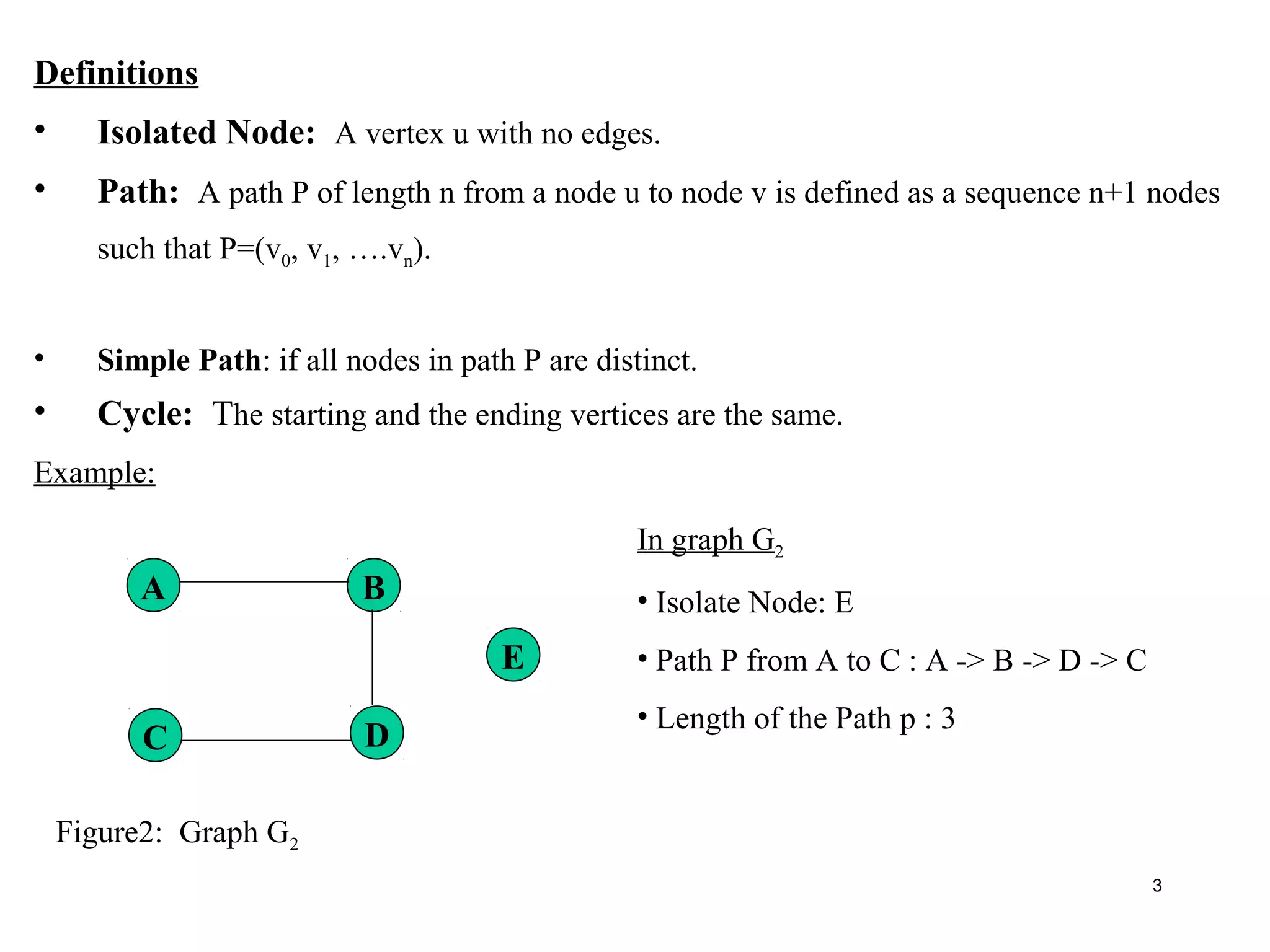
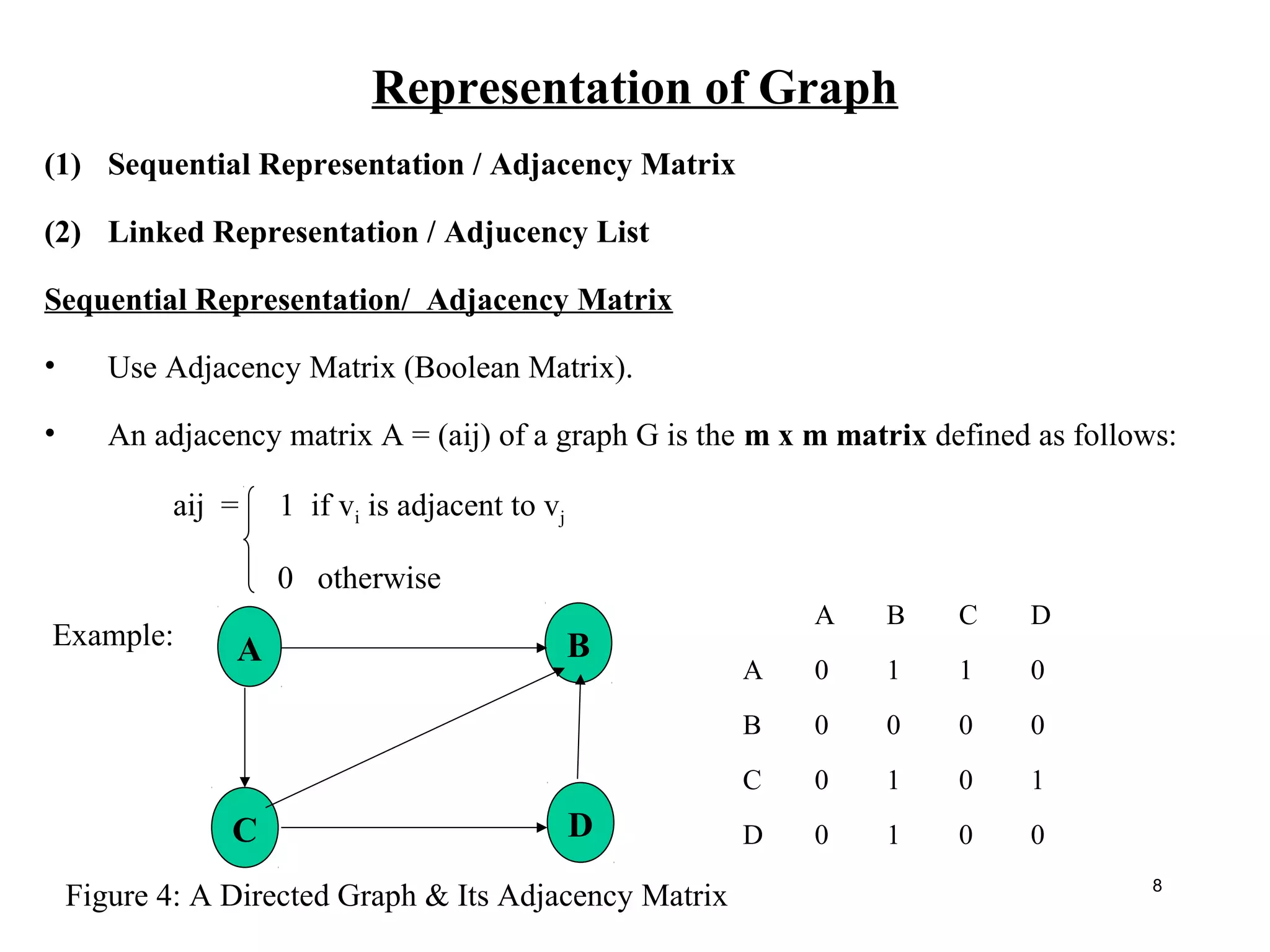
• A graph G consists of two properties:
(a) A set V of elements called vertices or nodes.
(b) A set E of connectors called edges such that each edge e is identified as
e = (u,v) (unordered pair of vertices). Here is a edge between u and v and
they are said to be the adjacent nodes or neighbors .
 The order of a graph is |V| (the number of vertices).
 A graph's size is |E|, the number of edges.
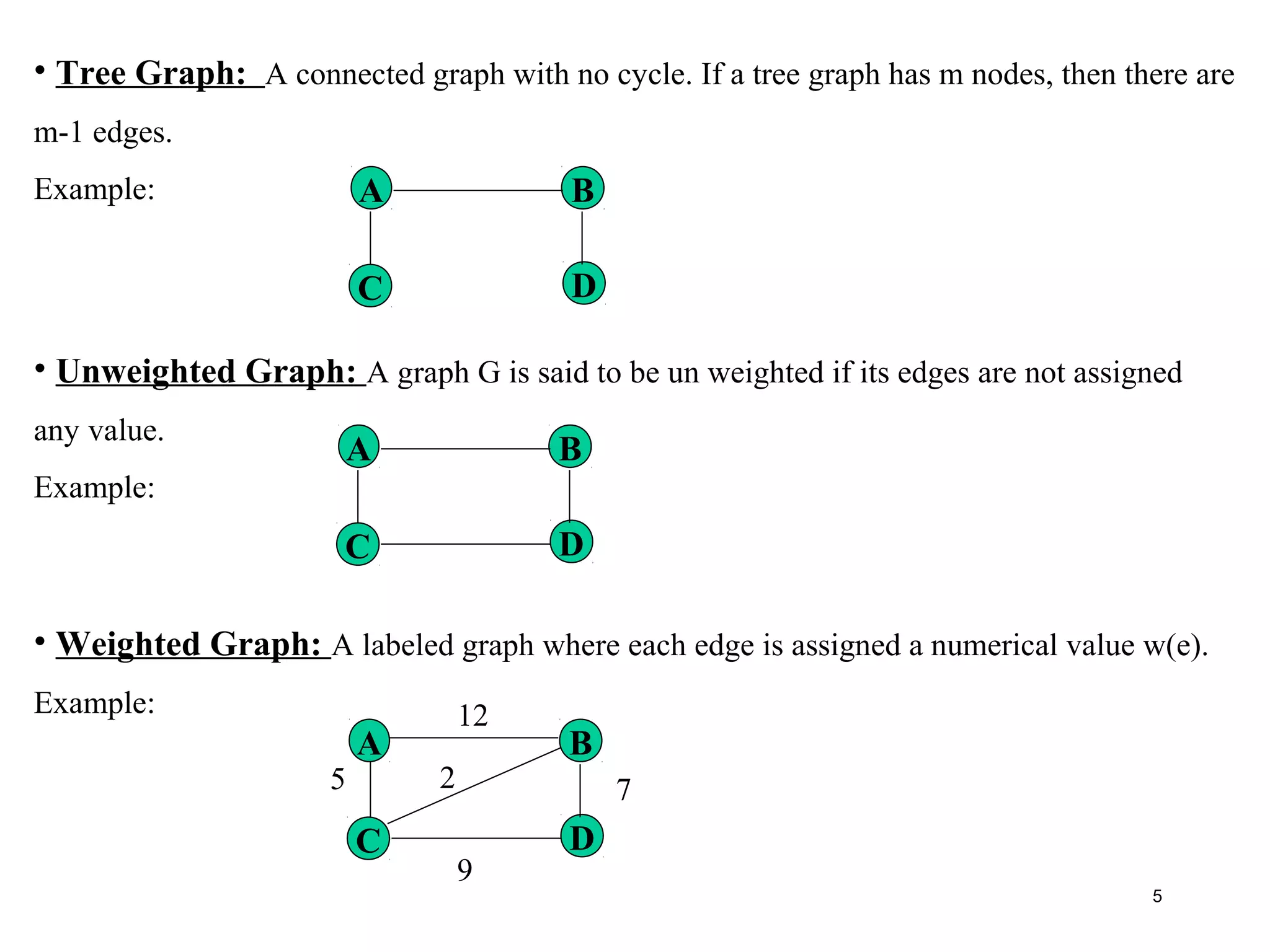
 A tree is a graph with no cycle.
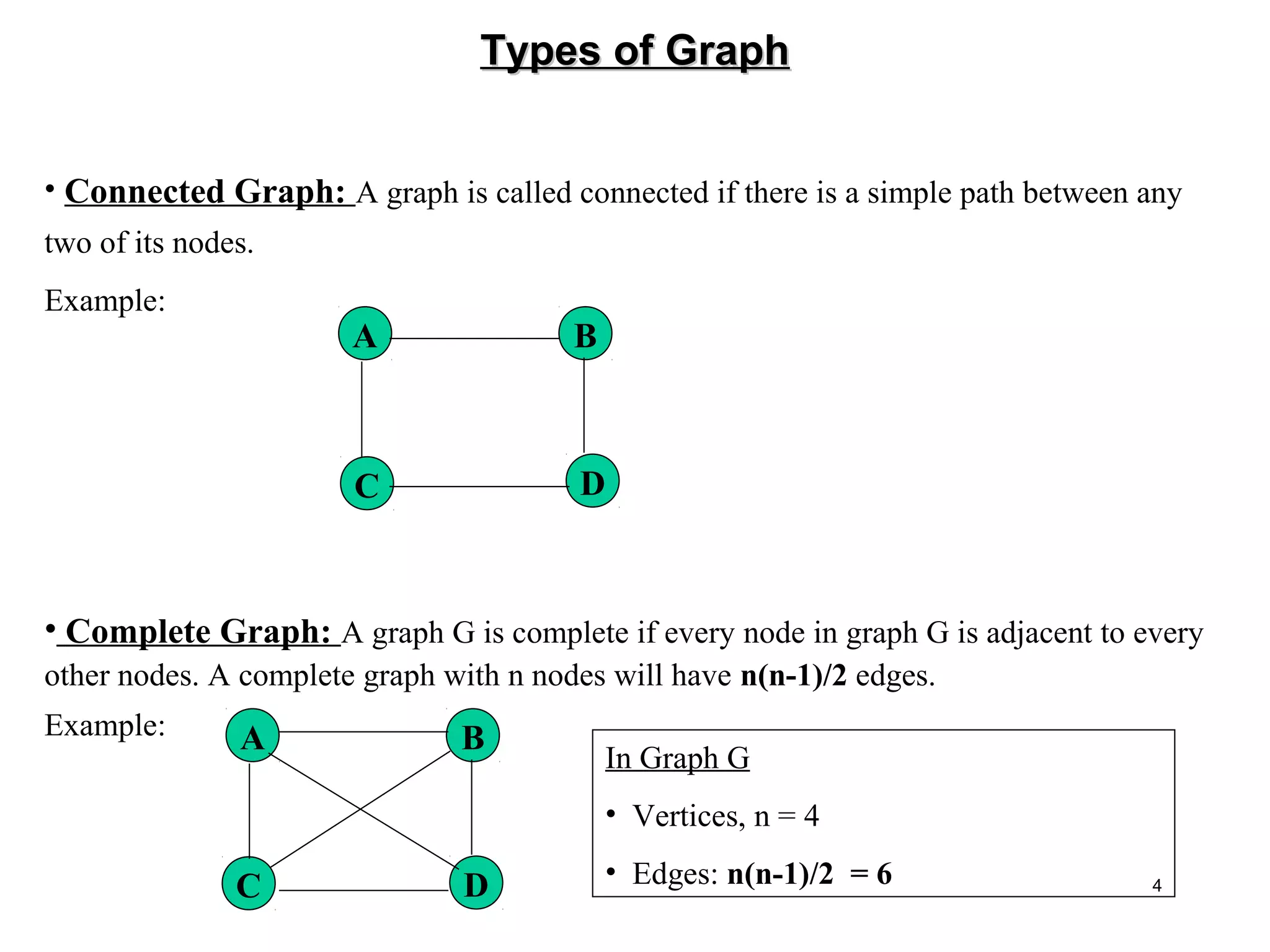
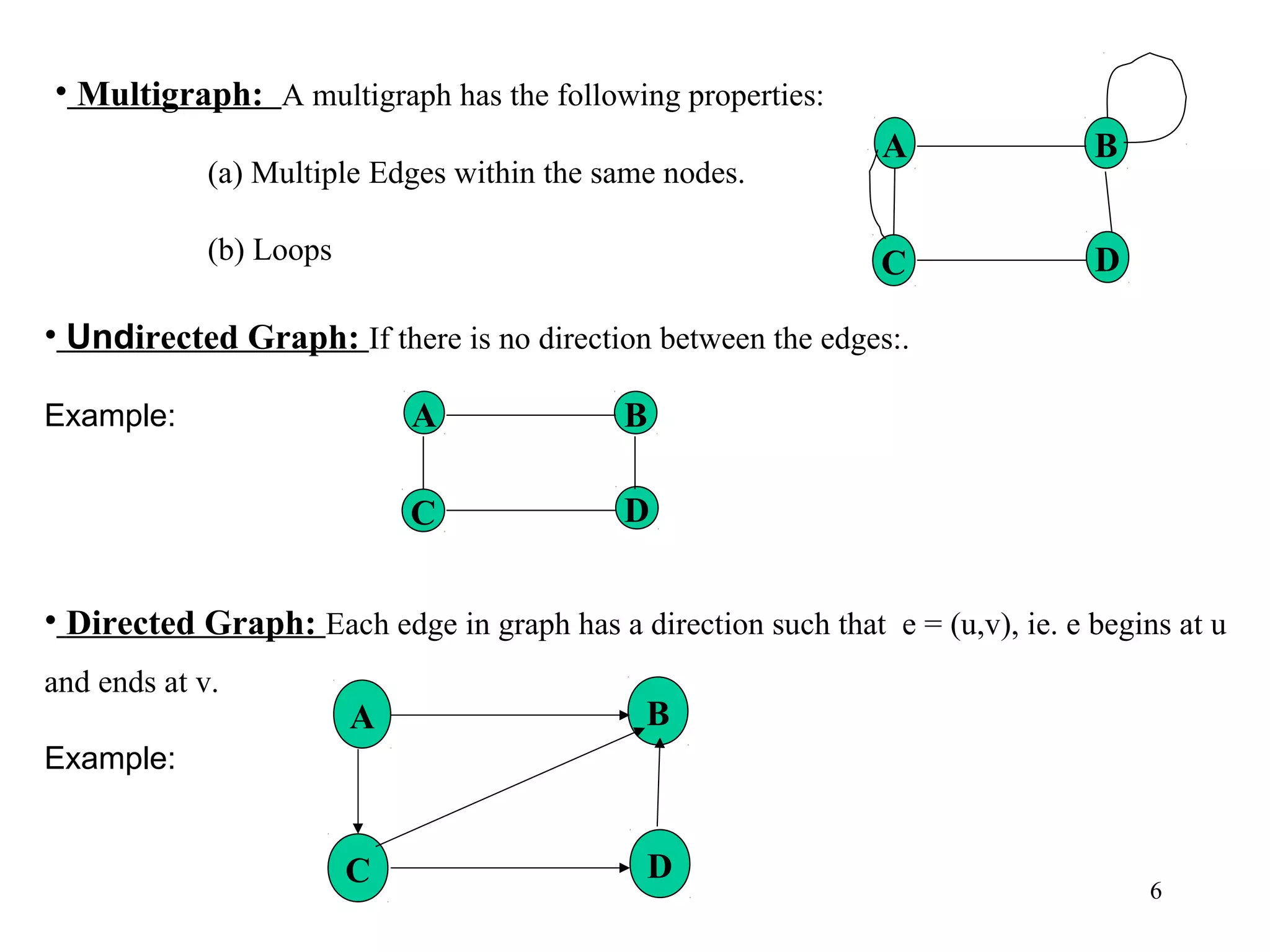
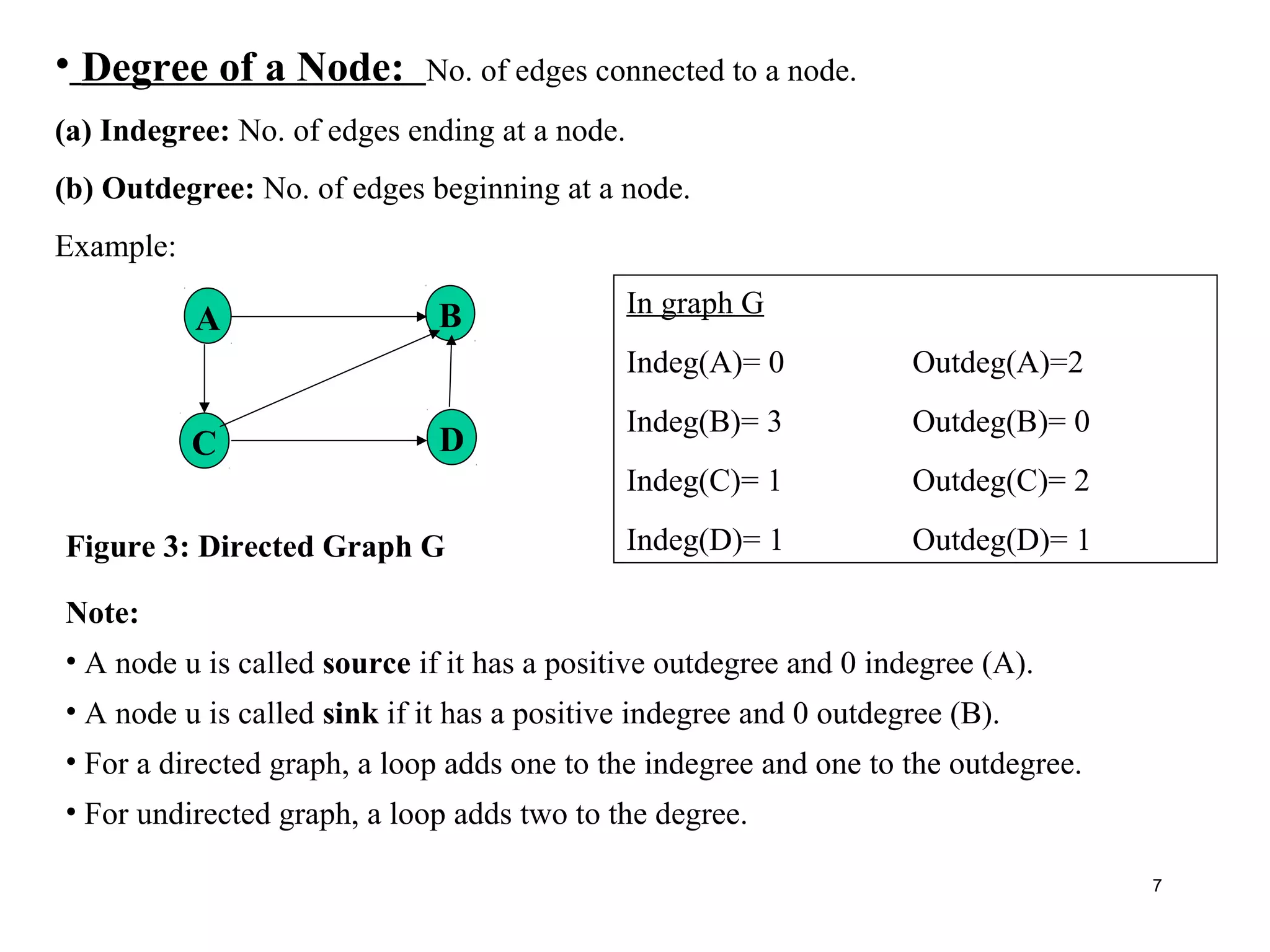
Example:
A B
C D
E
In Graph G1
• 5 Vertices:{A, B, C, D, E}
• 6 Edges: {[A,B], [A,C], [B,D],
[B,E], [C,D], [D,E]}
Figure1: A graph G1
GraphGraph
2

3. Definitions
• Isolated Node: A vertex u with no edges.
• Path: A path P of length n from a node u to node v is defined as a sequence n+1 nodes
such that P=(v0, v1, ….vn).
• Simple Path: if all nodes in path P are distinct.
• Cycle: The starting and the ending vertices are the same.
Example:
A B
C D
E
In graph G2
• Isolate Node: E
• Path P from A to C : A -> B -> D -> C
• Length of the Path p : 3
Figure2: Graph G2
3

4. • Connected Graph: A graph is called connected if there is a simple path between any
two of its nodes.
Example:
• Complete Graph: A graph G is complete if every node in graph G is adjacent to every
other nodes. A complete graph with n nodes will have n(n-1)/2 edges.
Example:
C
A B
D
A B
C D
4
Types of GraphTypes of Graph
In Graph G
• Vertices, n = 4
• Edges: n(n-1)/2 = 6

5. • Tree Graph: A connected graph with no cycle. If a tree graph has m nodes, then there are
m-1 edges.
Example:
• Unweighted Graph: A graph G is said to be un weighted if its edges are not assigned
any value.
Example:
• Weighted Graph: A labeled graph where each edge is assigned a numerical value w(e).
Example:
A B
C D
A B
C D
A B
C D
5
12
7
9
2
5

6. • Multigraph: A multigraph has the following properties:
(a) Multiple Edges within the same nodes.
(b) Loops
• Directed Graph: Each edge in graph has a direction such that e = (u,v), ie. e begins at u
and ends at v.
Example:
A B
C D
A B
C D
6
• Undirected Graph: If there is no direction between the edges:.
Example: A B
C D

7. • Degree of a Node: No. of edges connected to a node.
(a) Indegree: No. of edges ending at a node.
(b) Outdegree: No. of edges beginning at a node.
Example:
A B
C D
In graph G
Indeg(A)= 0 Outdeg(A)=2
Indeg(B)= 3 Outdeg(B)= 0
Indeg(C)= 1 Outdeg(C)= 2
Indeg(D)= 1 Outdeg(D)= 1Figure 3: Directed Graph G
Note:
• A node u is called source if it has a positive outdegree and 0 indegree (A).
• A node u is called sink if it has a positive indegree and 0 outdegree (B).
• For a directed graph, a loop adds one to the indegree and one to the outdegree.
• For undirected graph, a loop adds two to the degree.
7

8. Representation of Graph
(1) Sequential Representation / Adjacency Matrix
(2) Linked Representation / Adjucency List
Sequential Representation/ Adjacency Matrix
• Use Adjacency Matrix (Boolean Matrix).
• An adjacency matrix A = (aij) of a graph G is the m x m matrix defined as follows:
aij = 1 if vi is adjacent to vj
0 otherwise
Example: A B
C D
A B C D
A 0 1 1 0
B 0 0 0 0
C 0 1 0 1
D 0 1 0 0
Figure 4: A Directed Graph & Its Adjacency Matrix 8

9. Adjacency matrix representation
of a weighted graph
9

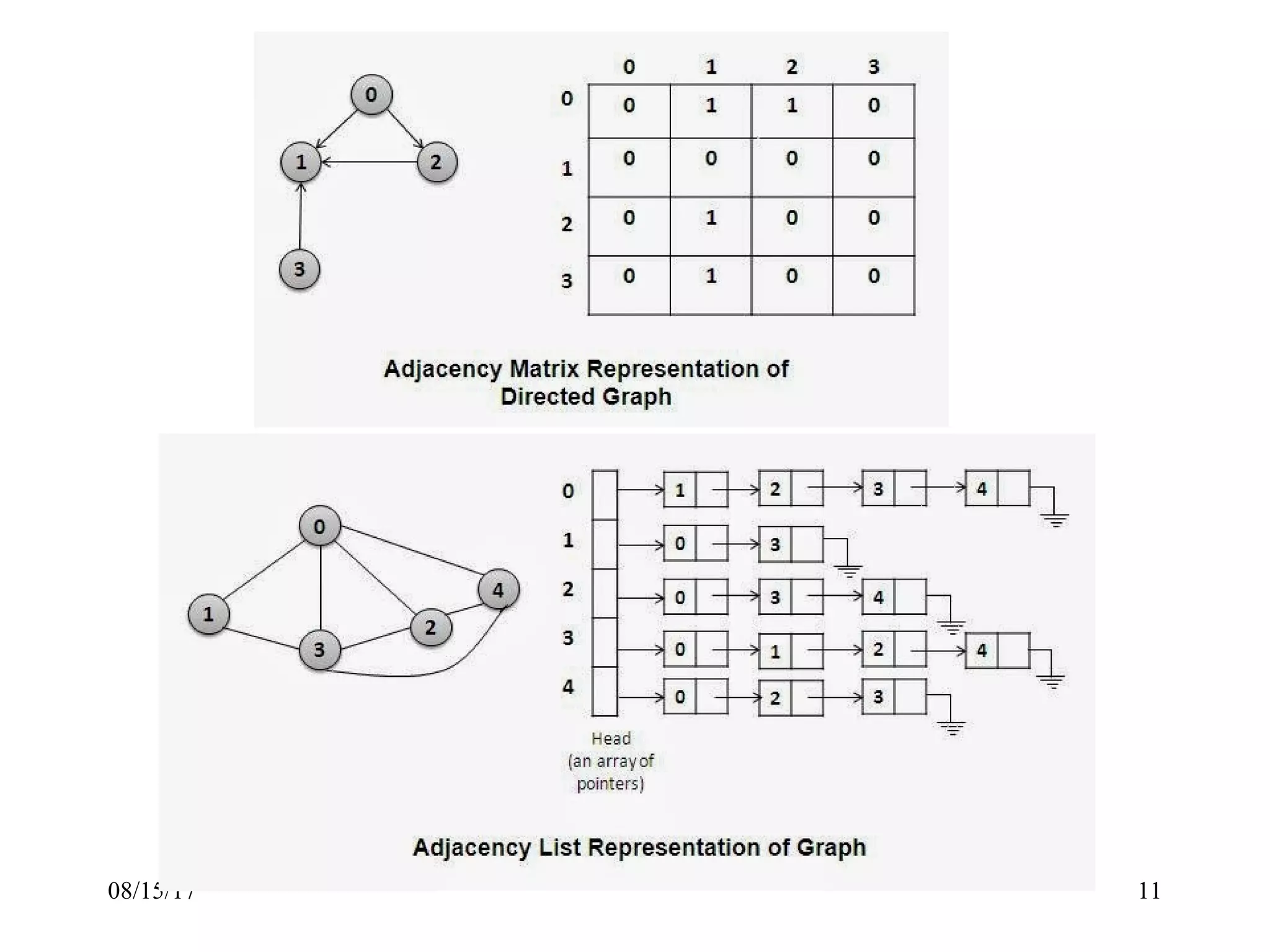
10. Linked Representation of a GraphLinked Representation of a Graph
•Adjacency List:
An array of linked lists is used. Size of the array is equal to number of vertices. Let the
array be array[]. An entry array[i] represents the linked list of vertices adjacent to the ith
vertex. This representation can also be used to represent a weighted graph. The weights of
edges can be stored in nodes of linked lists. Following is adjacency list representation of
the above graph.
Example:
Figure: Directed Graph and Corresponding Adjacency List
10

11. 08/15/17 11

12. Which Representation Is Better?
• The adjacency-list is usually preferred if the graph is sparse (having few edges).
• The adjacency-matrix is preferred if the graph is dense (the number of edges is
close to the maximal number of edges).
If |E| ≈ |V|2
the graph is dense
If |E| ≈ |V| the graph is sparse
Dense Graph Sparse Graph
Figure: Dense and Sparse Graph
12

13. 13
END!!!