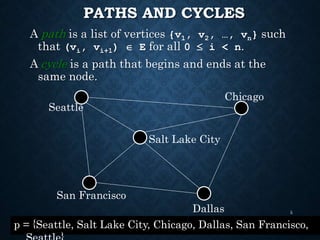
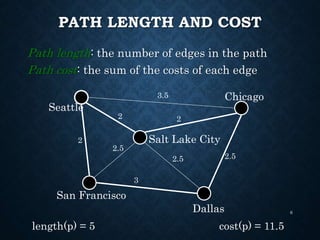
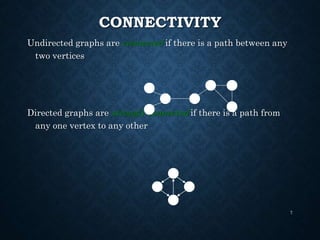
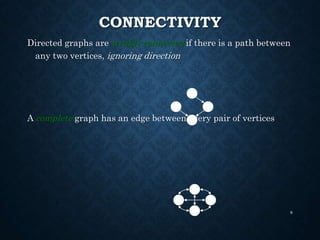
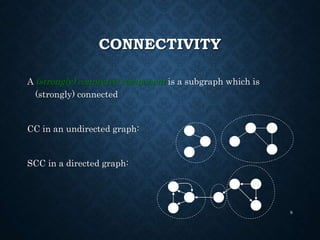
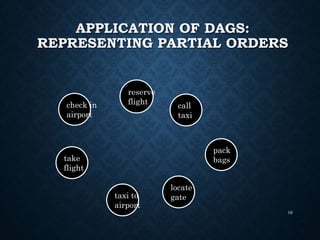
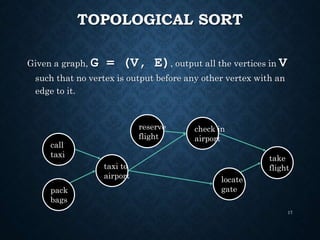
The document details the structure and properties of graphs, which represent relationships among objects through vertices and edges. It explains directed and undirected graphs, their weighted versions, paths, cycles, connectivity, and various applications including trees and directed acyclic graphs (DAGs). Additionally, it covers graph representation techniques and introduces the concept of topological sorting.

1. DATA STRUCTURES:
GRAPHS
1

2. GRAPHS
Graphs = formalism for representing relationships between objects
• A graph G = (V, E)
• V is a set of vertices
• E  V  V is a set of edges
2
Han
Leia
Luke
V = {Han, Leia, Luke}
E = {(Luke, Leia),
(Han, Leia),
(Leia, Han)}

3. DIRECTED VS. UNDIRECTED
GRAPHS
• In directed graphs, edges have a specific direction:
• In undirected graphs, they don’t (edges are two-way):
• Vertices u and v are adjacent if (u, v)  E
3
Han
Leia
Luke
Han
Leia
Luke

4. WEIGHTED GRAPHS
4
20
30
35
60
Mukilteo
Edmonds
Seattle
Bremerton
Bainbridge
Kingston
Clinton
There may be more
information in the graph as well.
Each edge has an associated weight or cost.

5. PATHS AND CYCLES
A path is a list of vertices {v1, v2, …, vn} such
that (vi, vi+1)  E for all 0  i < n.
A cycle is a path that begins and ends at the
same node.
5
Seattle
San Francisco
Dallas
Chicago
Salt Lake City
p = {Seattle, Salt Lake City, Chicago, Dallas, San Francisco,

6. PATH LENGTH AND COST
Path length: the number of edges in the path
Path cost: the sum of the costs of each edge
6
Seattle
San Francisco
Dallas
Chicago
Salt Lake City
3.5
2 2
2.5
3
2
2.5
2.5
length(p) = 5 cost(p) = 11.5

7. CONNECTIVITY
Undirected graphs are connected if there is a path between any
two vertices
Directed graphs are strongly connected if there is a path from
any one vertex to any other
7

8. CONNECTIVITY
Directed graphs are weakly connected if there is a path between
any two vertices, ignoring direction
A complete graph has an edge between every pair of vertices
8

9. CONNECTIVITY
A (strongly) connected component is a subgraph which is
(strongly) connected
CC in an undirected graph:
SCC in a directed graph:
9

10. DISTANCE AND DIAMETER
• The distance between two nodes, d(u,v), is the
length of the shortest paths, or  if there is no path
• The diameter of a graph is the largest distance
between any two nodes
• Graph is strongly connected iff diameter < 
10

11. OTHER GRAPHS
• Geography:
• Cities and roads
• Airports and flights (diameter  20 !!)
• Publications:
• The co-authorship graph
• E.g. the Erdos distance
• The reference graph
• Phone calls: who calls whom
• Almost everything can be modeled as a graph !
11

12. GRAPH REPRESENTATION 1:
ADJACENCY MATRIX
A |V| x |V| array in which an element (u, v) is
true if and only if there is an edge from u to v
12
Han
Leia
Luke
Han Luke Leia
Han
Luke
LeiaRuntime:
iterate over vertices
iterate ever edges
iterate edges adj. to vertex
edge exists?
Space requirements:

13. GRAPH REPRESENTATION 2:
ADJACENCY LIST
A |V|-ary list (array) in which each entry stores a list (linked
list) of all adjacent vertices
13
Han
Leia
Luke
Han
Luke
Leia
space requirements:
Runtime:
iterate over vertices
iterate ever edges
iterate edges adj. to vertex
edge exists?

14. TREES AS GRAPHS
• Every tree is a graph with some
restrictions:
• the tree is directed
• there are no cycles (directed or
undirected)
• there is a directed path from the
root to every node
14
A
B
D E
C
F
HG
JI
BAD!

15. DIRECTED ACYCLIC GRAPHS
(DAGS)
DAGs are directed graphs
with no cycles.
15
main()
add()
access()
mult()
read()
Trees  DAGs  Graphs
if program
call graph is a
DAG, then all
procedure
calls can be
in-lined

16. APPLICATION OF DAGS:
REPRESENTING PARTIAL ORDERS
16
check in
airport
call
taxi
taxi to
airport
reserve
flight
pack
bagstake
flight
locate
gate

17. TOPOLOGICAL SORT
Given a graph, G = (V, E), output all the vertices in V
such that no vertex is output before any other vertex with an
edge to it.
17
check in
airport
call
taxi
taxi to
airport
reserve
flight
pack
bags
take
flight
locate
gate

18. TOPOLOGICAL SORT
18
check in
airport
call
taxi
taxi to
airport
reserve
flight
pack
bags
take
flight
locate
gate