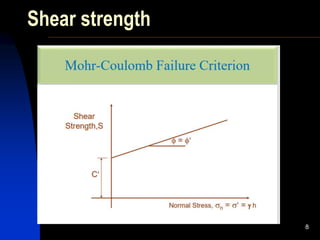
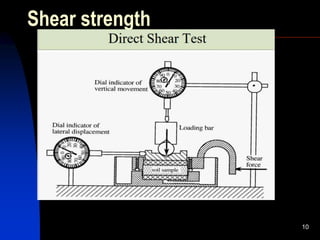
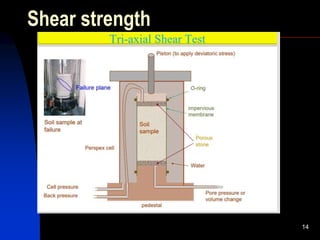
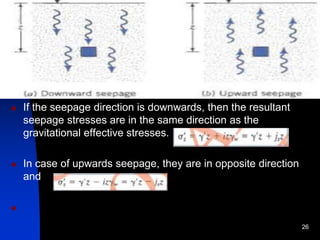
1. The document discusses various engineering properties of soil related to shear strength and permeability.
2. It explains that water flow through soil is governed by Darcy's Law, where the flow velocity is proportional to the hydraulic gradient.
3. The proportionality coefficient is called the coefficient of permeability or hydraulic conductivity, which is influenced by factors like void ratio and particle size.