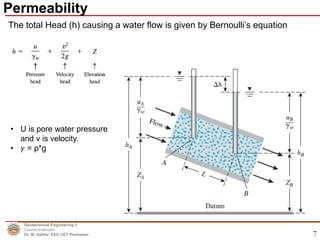
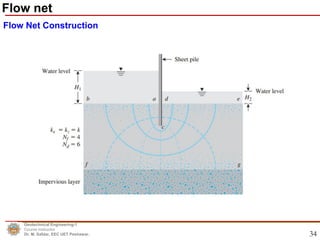
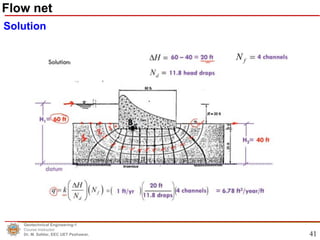
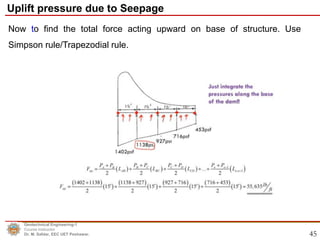
This document discusses permeability and seepage in geotechnical engineering. It begins by defining permeability as a measure of a soil's ability to allow water to flow through its pores or voids. It then discusses Darcy's law, which describes water flow through porous media, and how permeability/hydraulic conductivity is measured in the laboratory. The document also covers the Laplace equation for two-dimensional water flow and flow nets, which can be used to model groundwater flow patterns. It provides examples of how flow nets are constructed and how they can be used to calculate water flow and seepage pressures.