Uploaded byBruce Coulter
Unit 2 3D Geometry
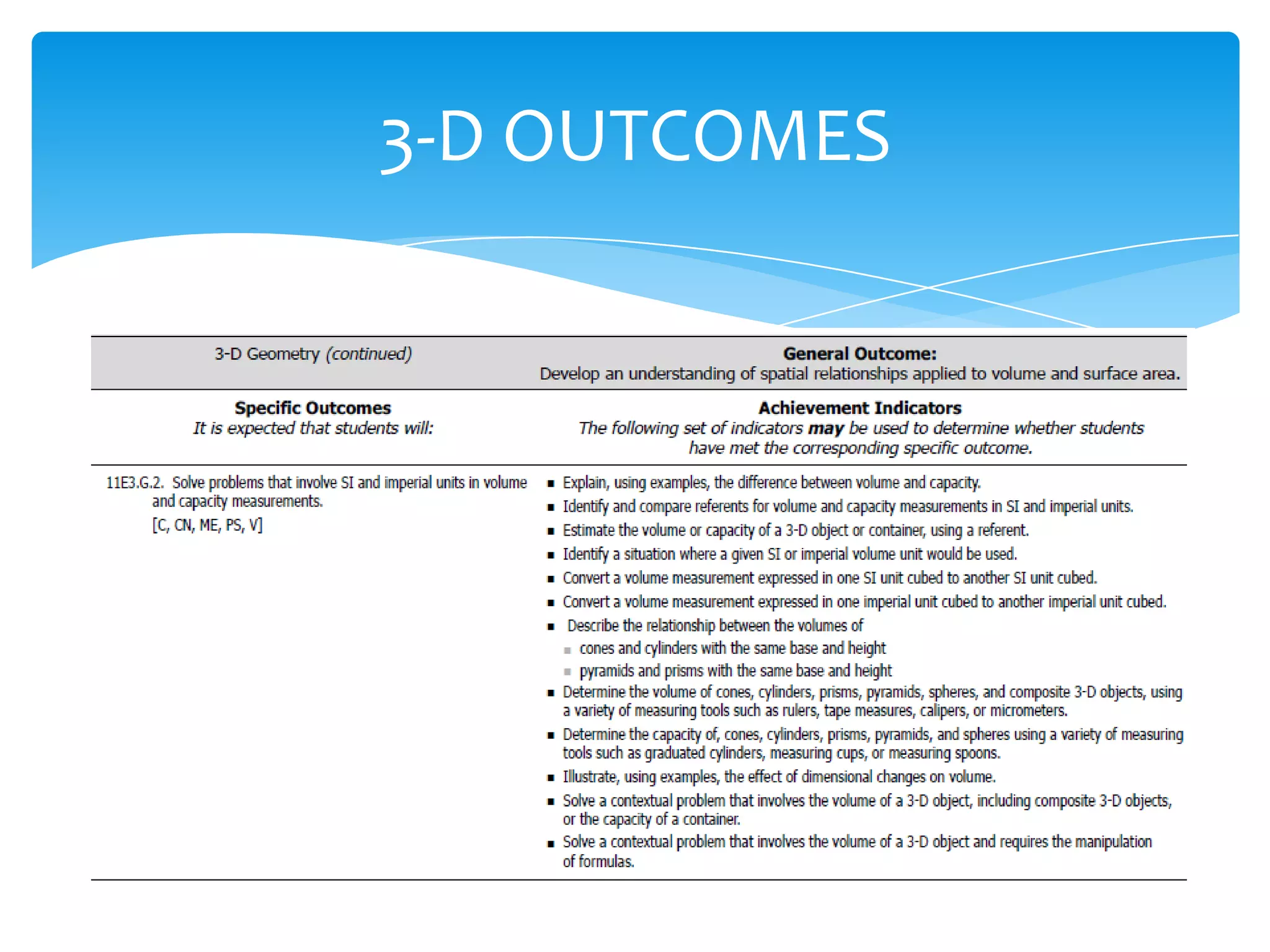
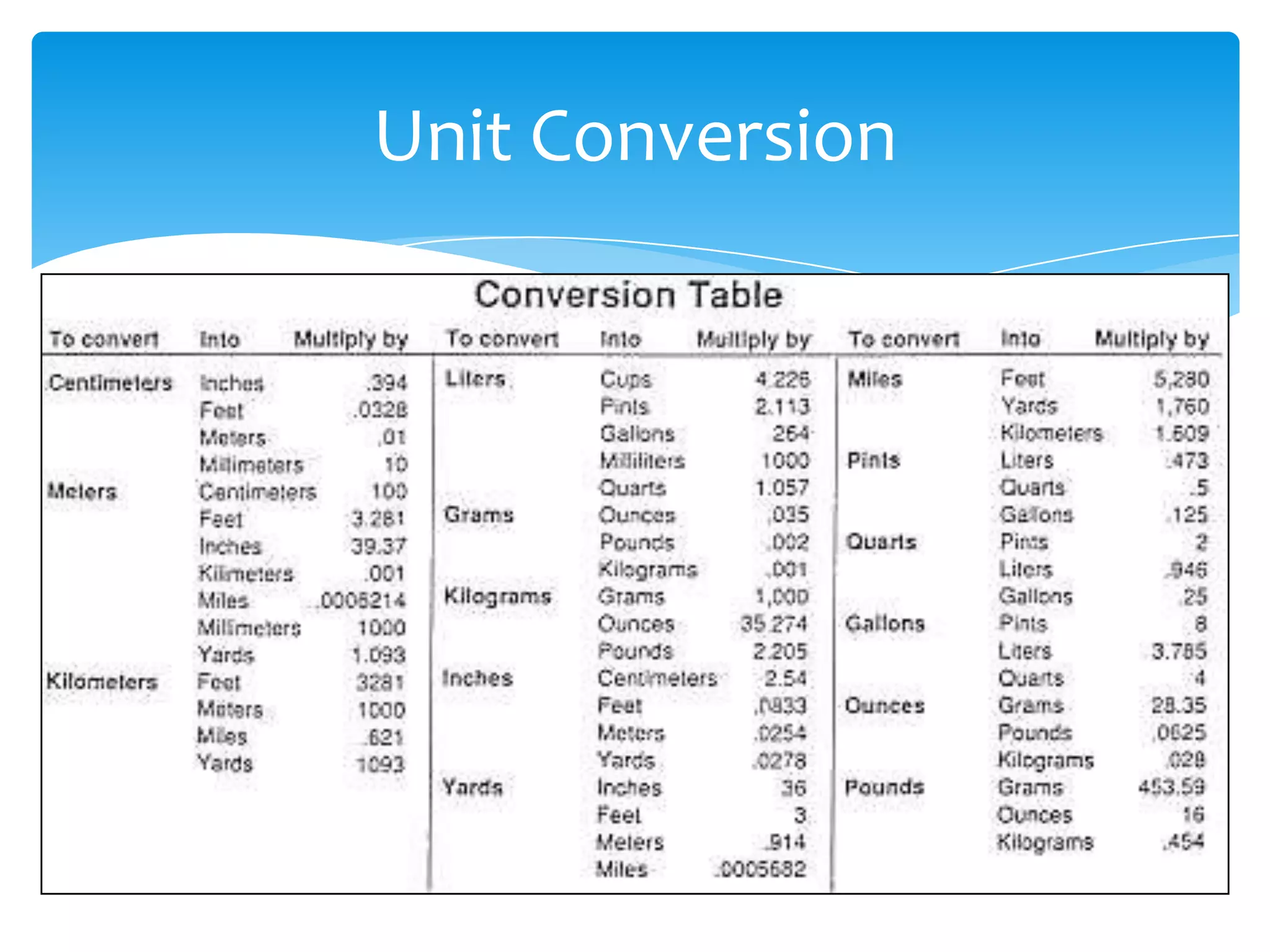
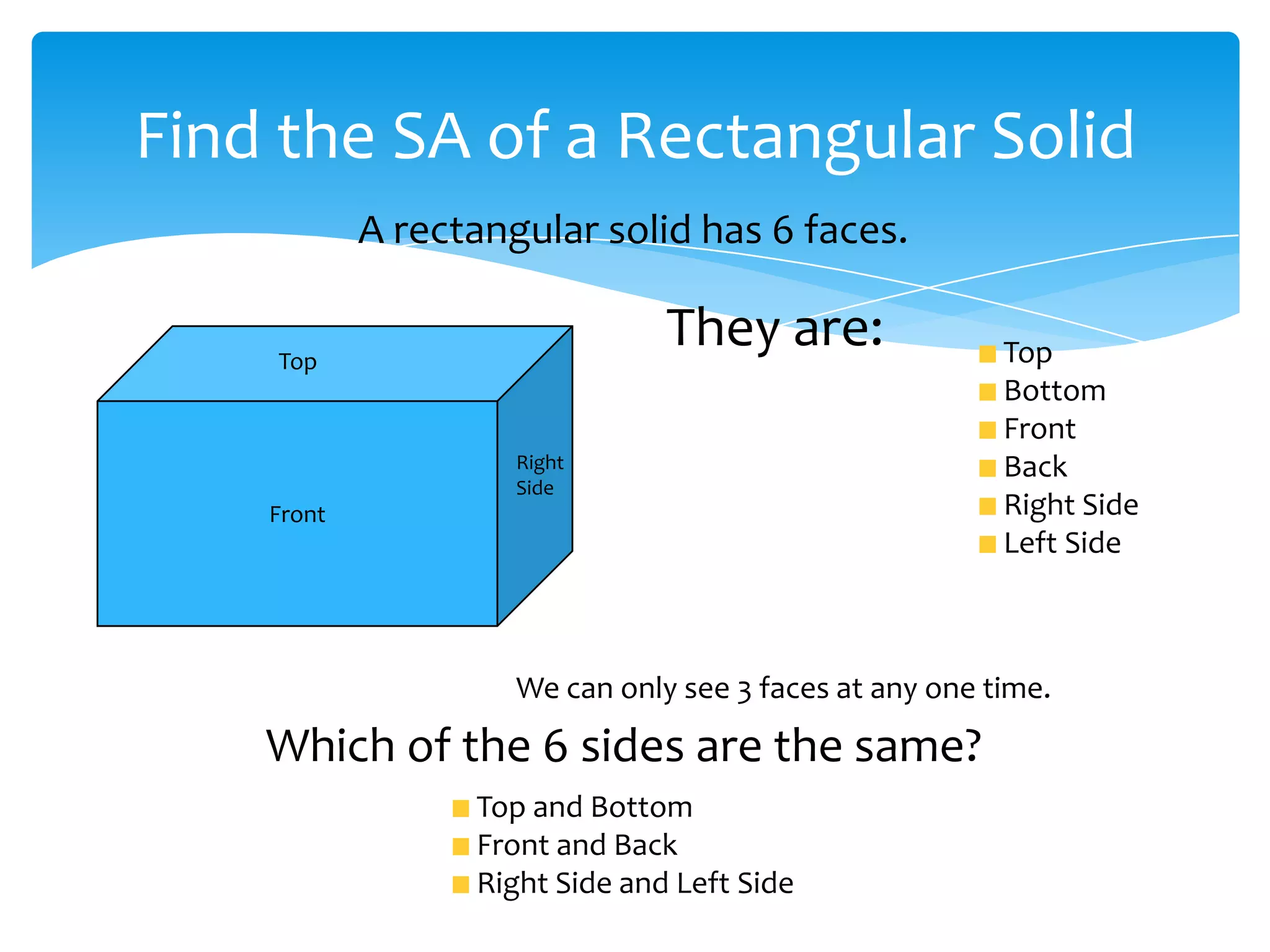
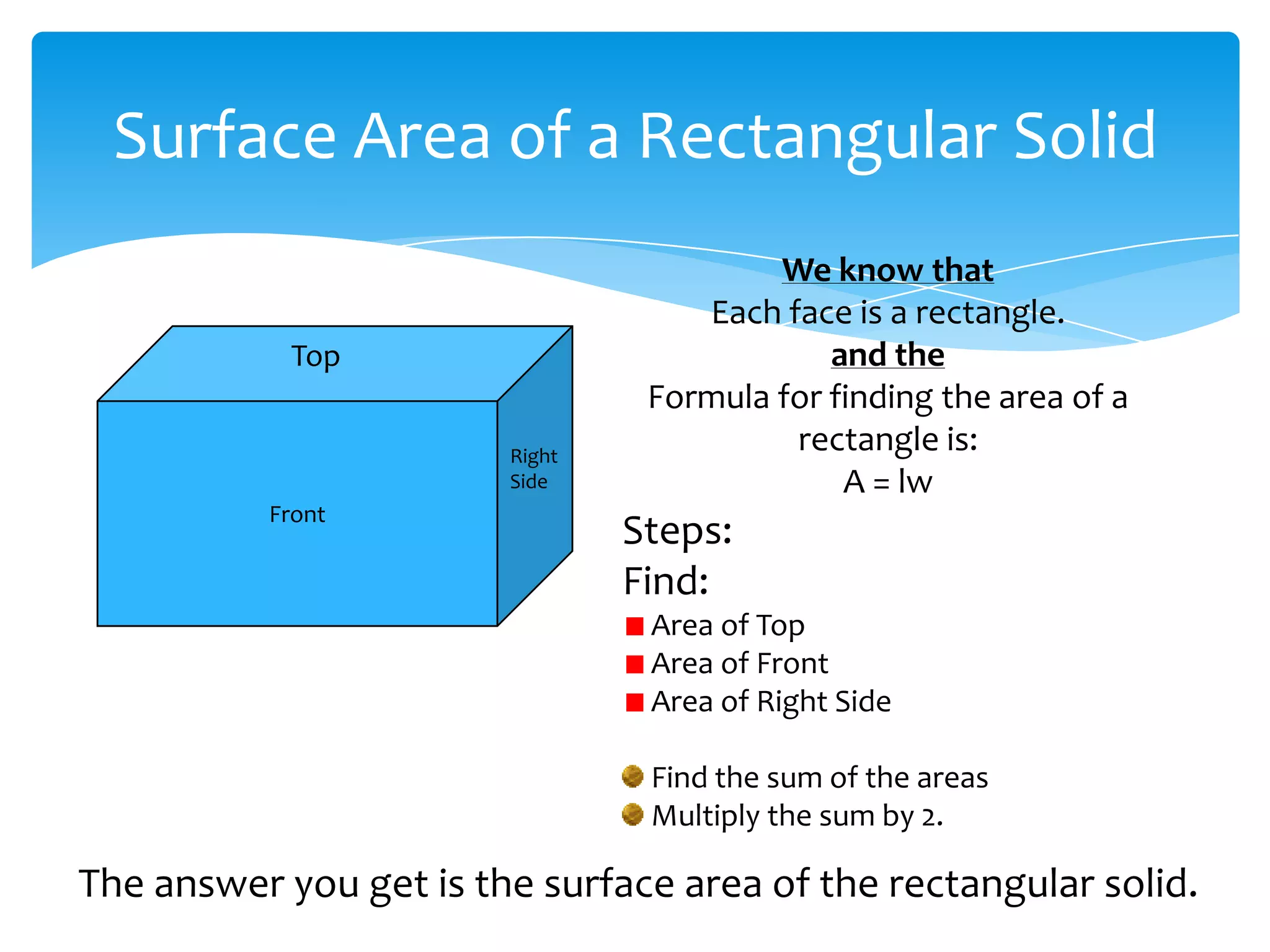
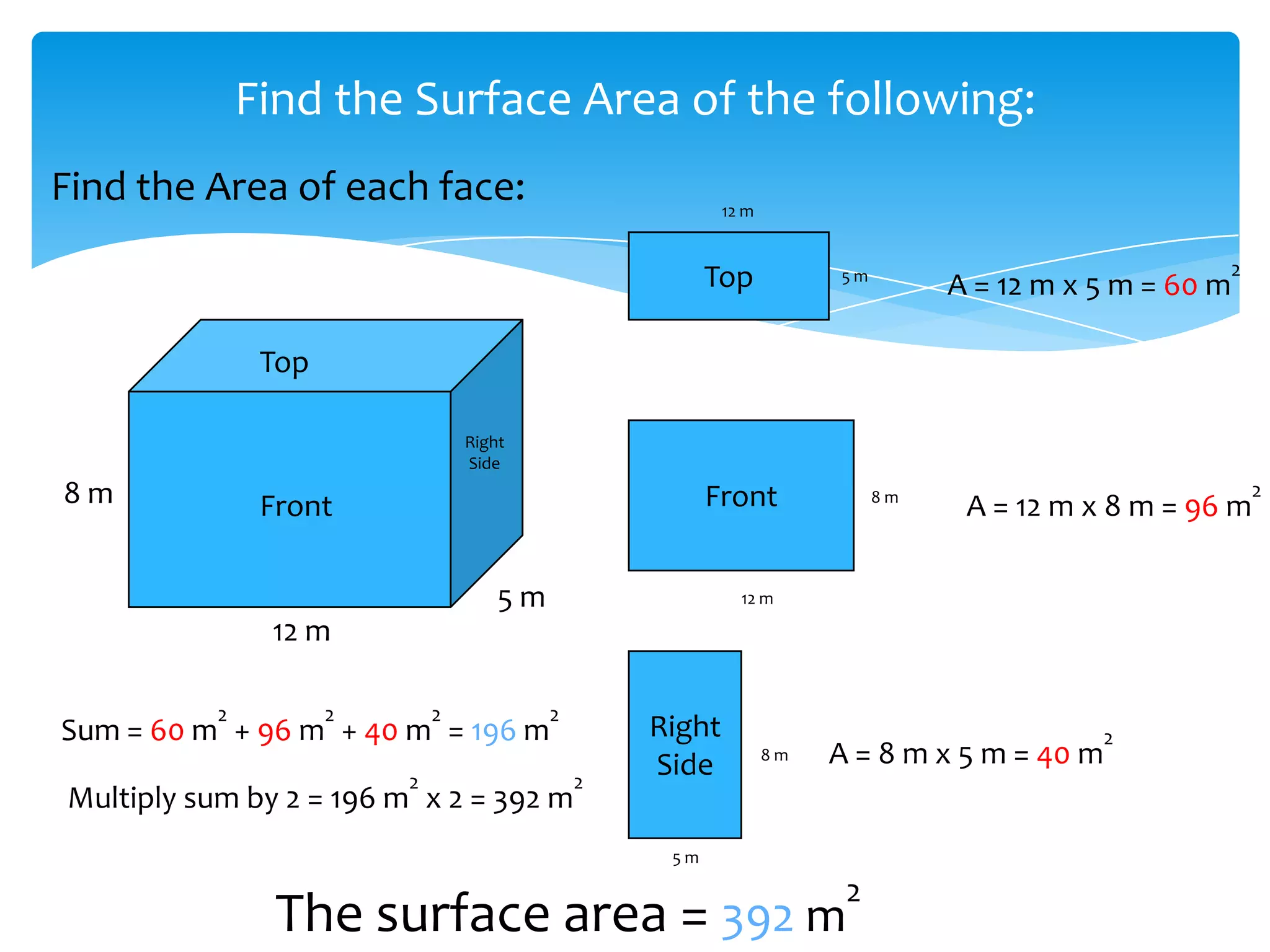
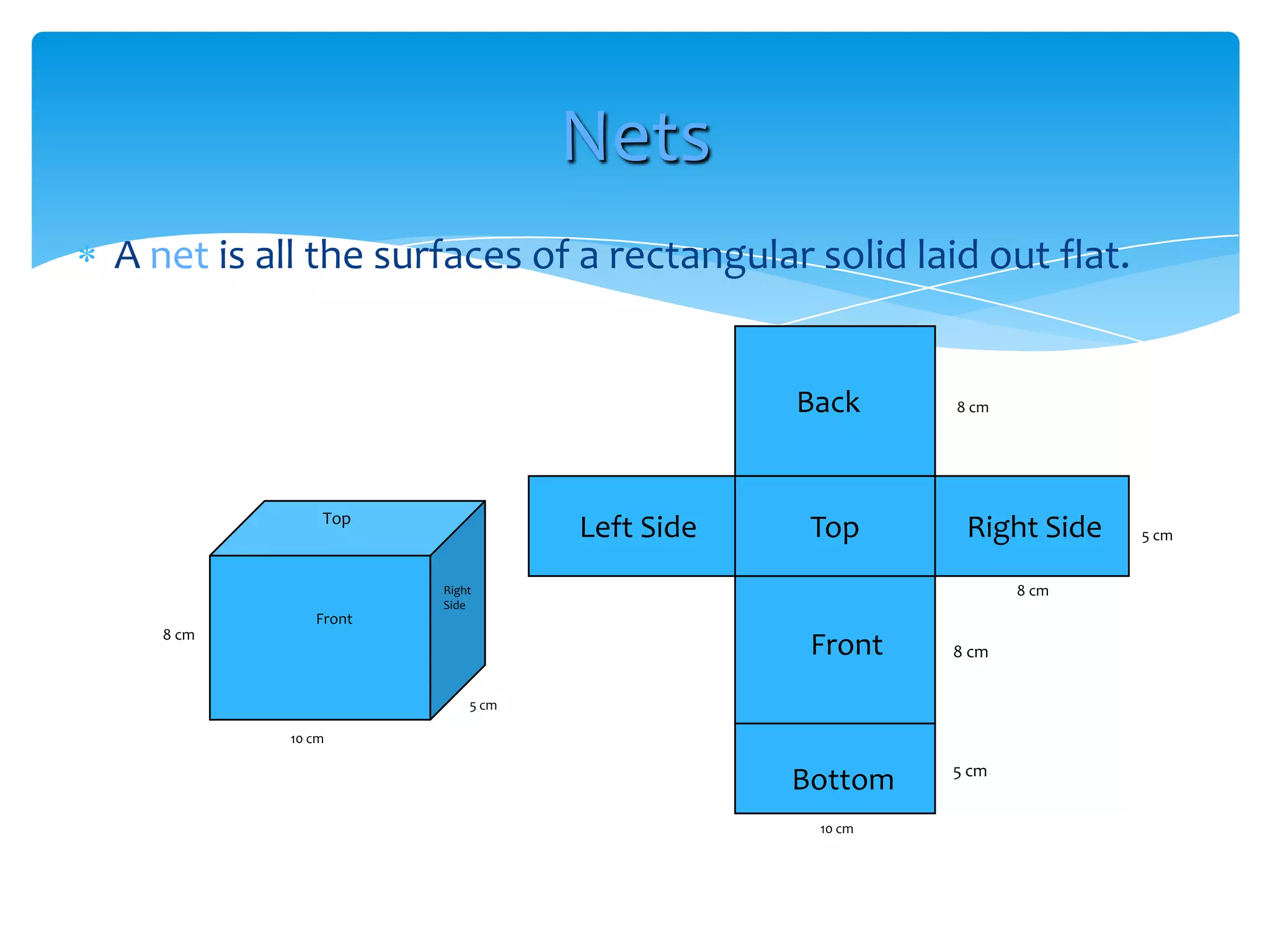
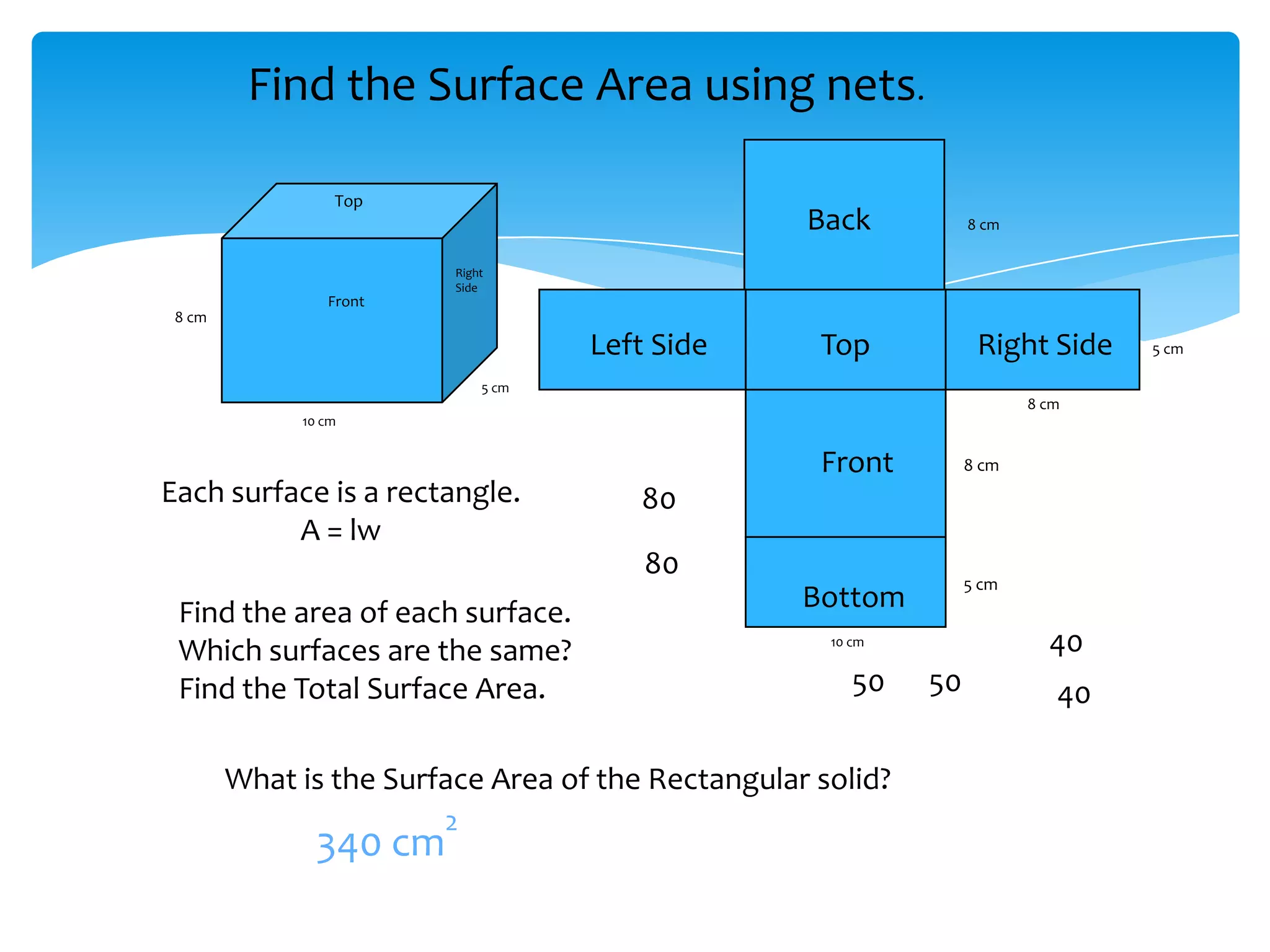
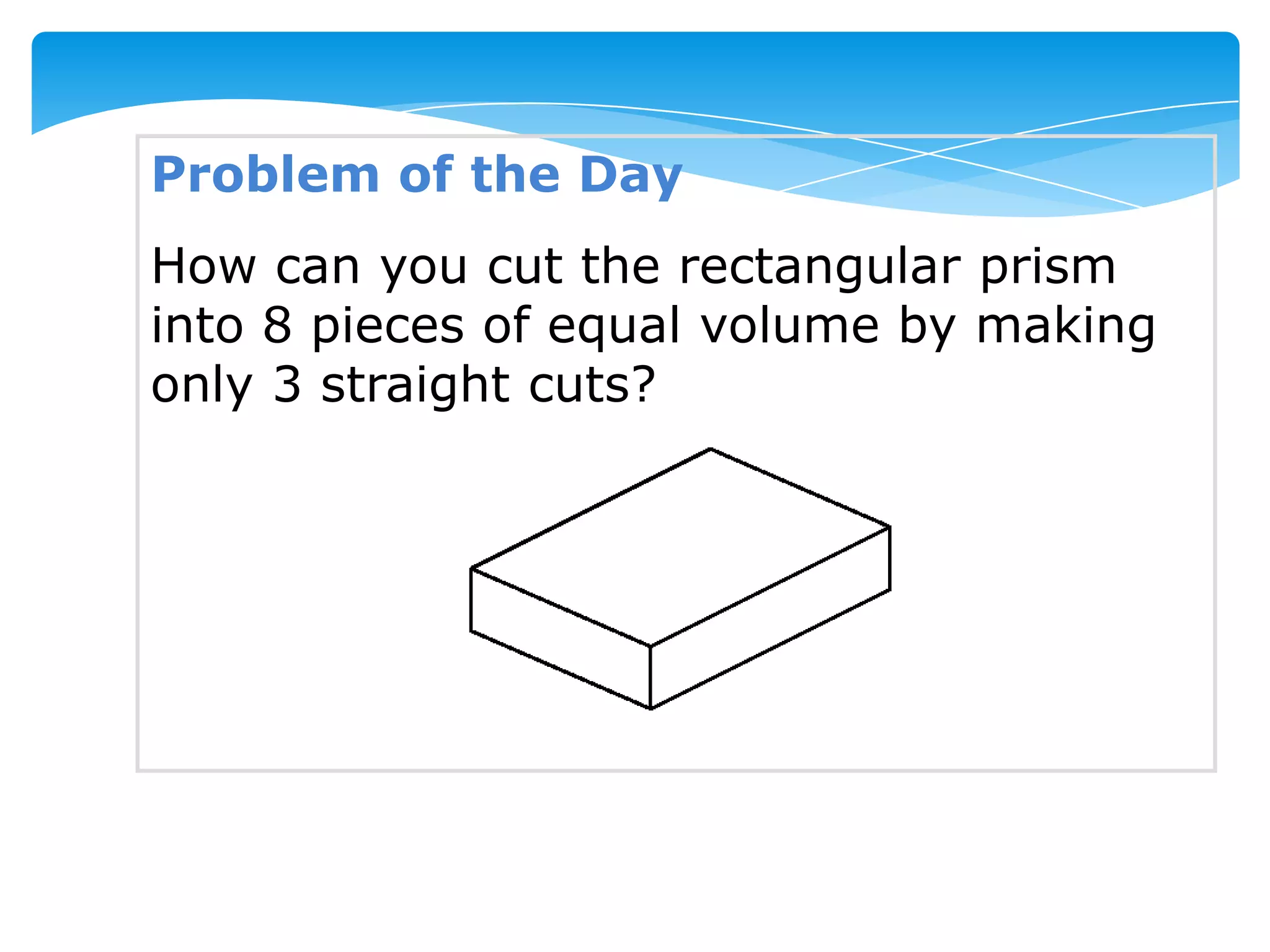
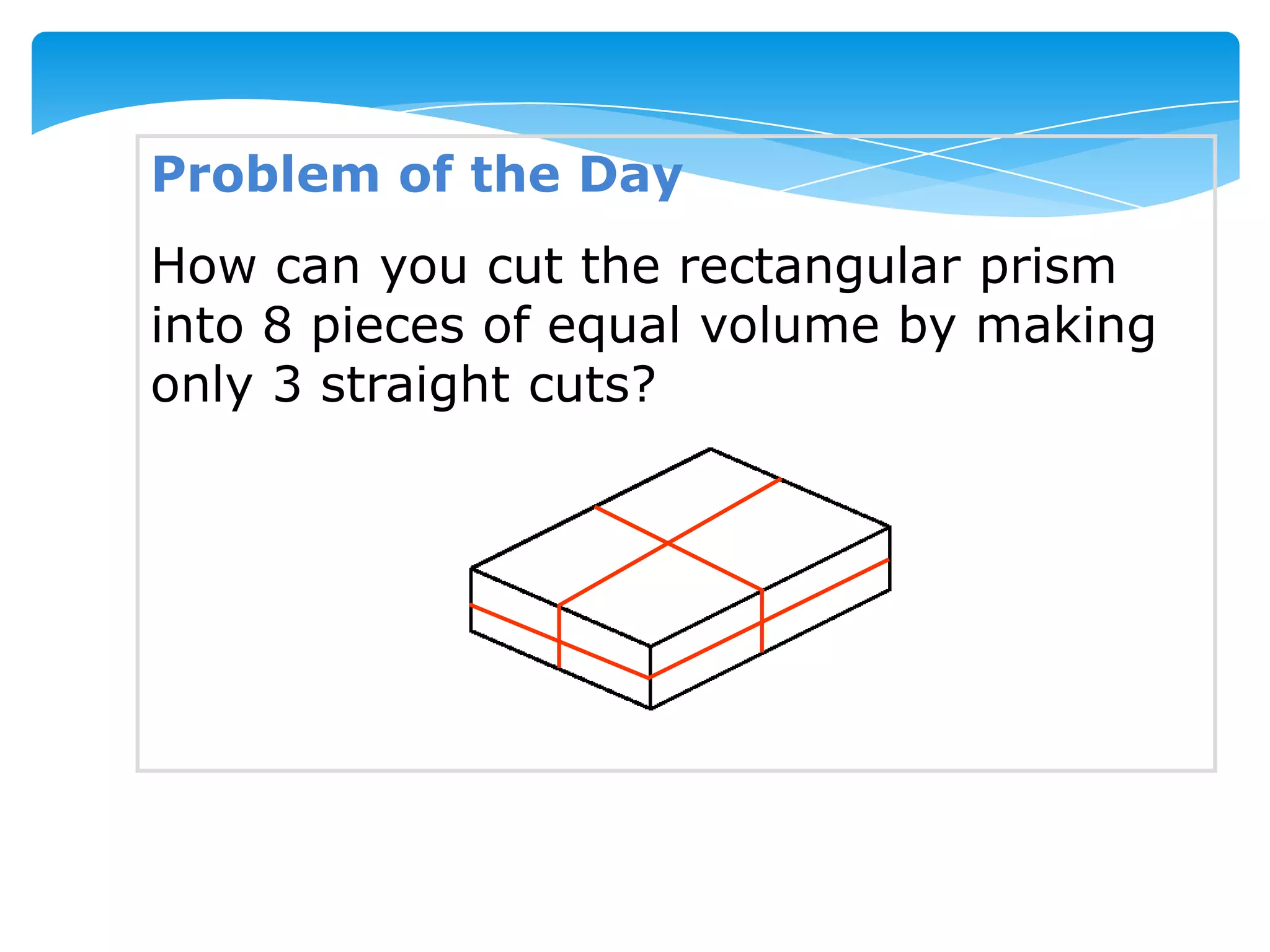
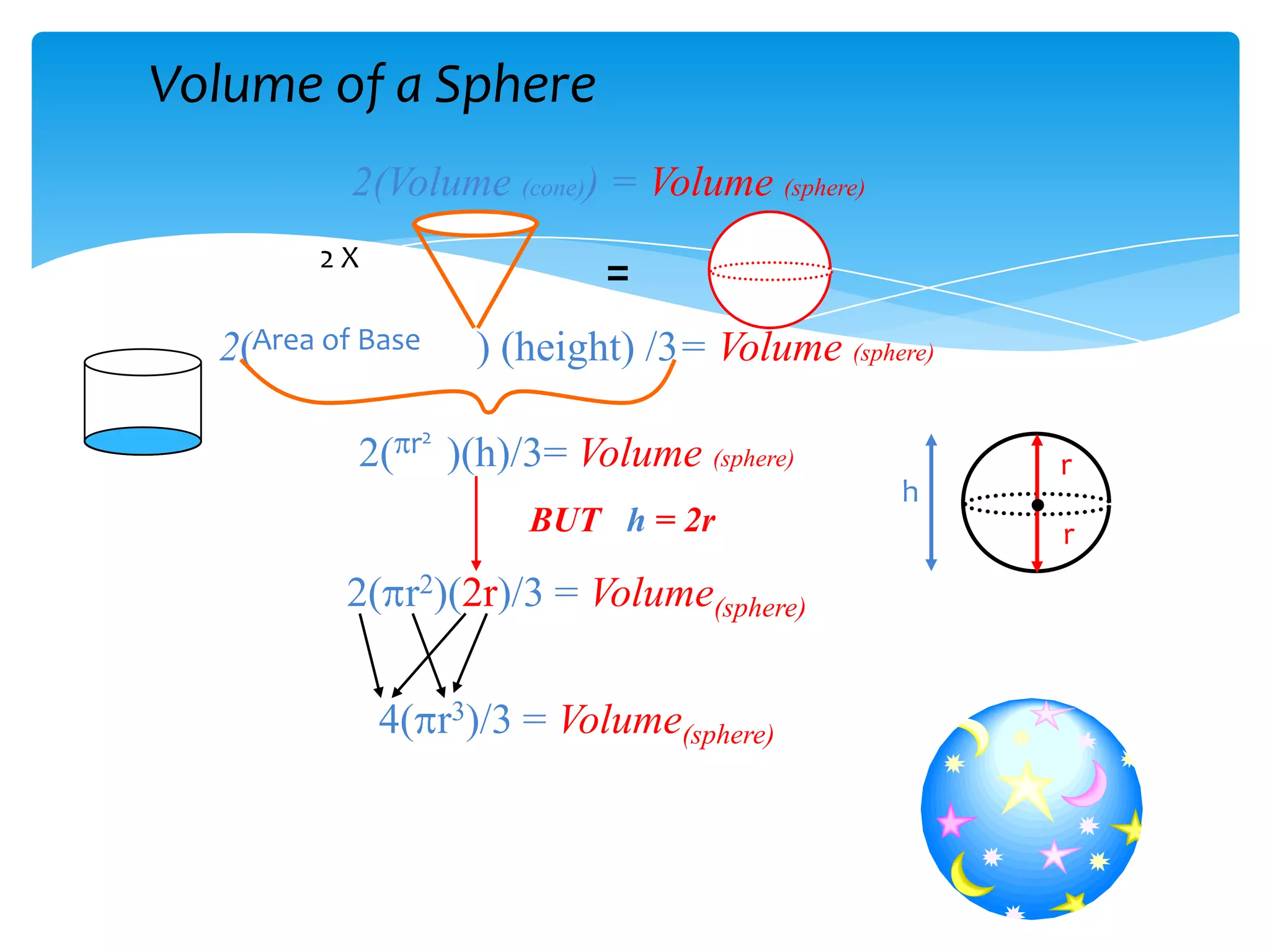
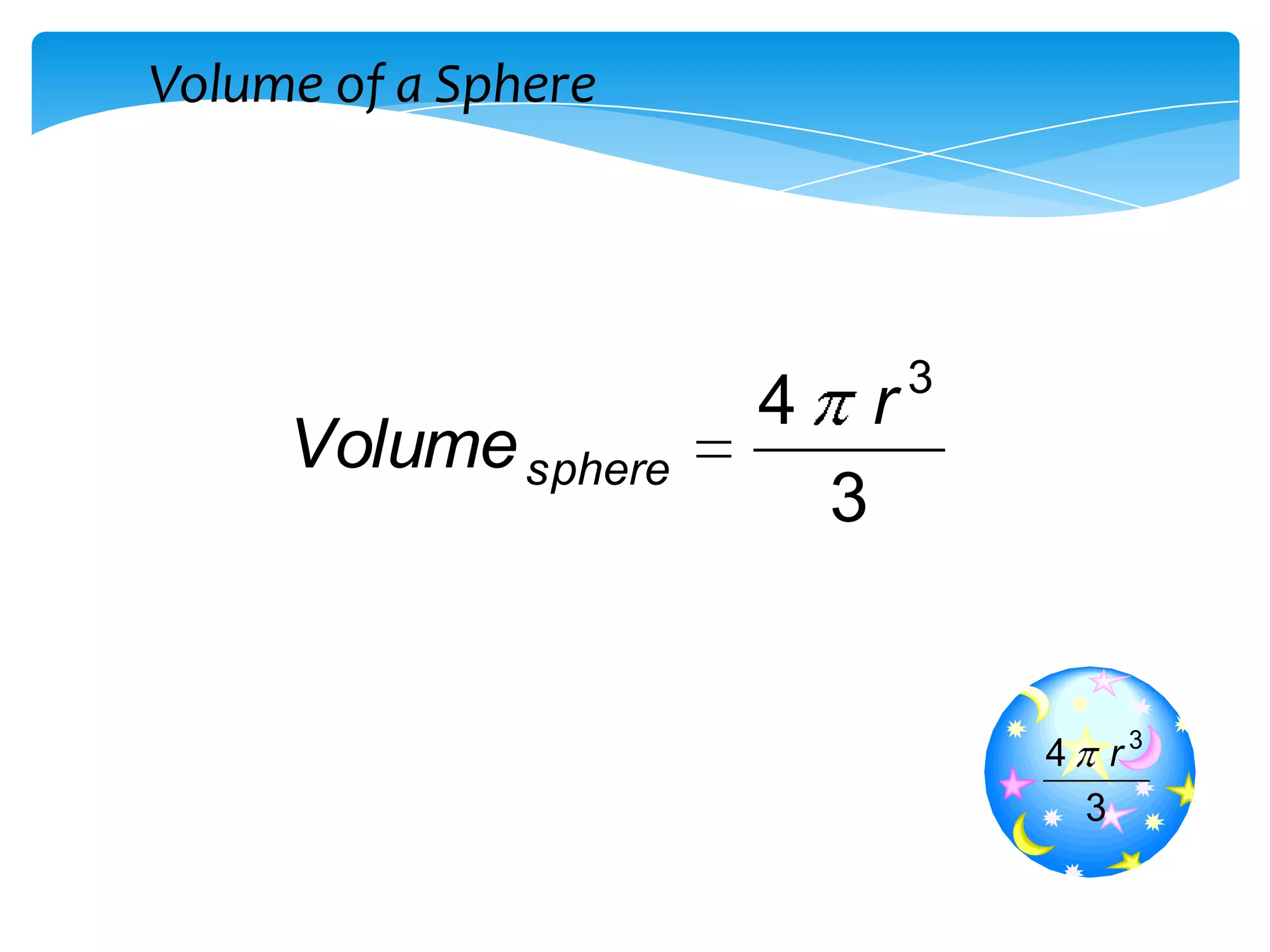
Okay, here are the steps: Radius (r) = 12 cm Volume of a sphere = (4/3)πr3 = (4/3)π(12cm)3 = (4/3)π × 13824 cm3 = 4488π cm3 Surface area of a sphere = 4πr2 = 4π(12cm)2 = 4π × 144 cm2 = 448π cm2 So the volume is 4488π cm3 and the surface area is 448π cm2.
More Related Content
Unit 2 3D Geometry
- 1. 3-D GEOMETRY Essential Math 30S
- 2.
- 3.
- 4.
- 5.
- 6.
- 7. History of Measurement ClassroomActivity (Page 196) Measure the items listed on page 196 using original body parts that underlay the measurement units listed. Record the measurements made by each person on the board and compare them.
- 8. History of Measurement StudentClass Door Book Desk
- 9. History of Measurement Notebook Assignment Page 198 – 200 Q. 1 - 7
- 10.
- 11.
- 12. Units of Measure Metric& Imperial Rulers •The following diagram shows a small ruler with the common metric (centimetres) and imperial (inches) units of linear measurement.
- 13. Units of Measure Metric& Imperial Rulers
- 14. Units of Measure Metric& Imperial Rulers
- 15. Units of Measure CommonMetric and Imperial Units of Length
- 16. Units of Measure NotebookAssignment Page 205 – 208 Q. 1 - 8
- 17.
- 18.
- 19.
- 20. Unit Conversion Metric •10 mm = 1 cm •100 cm = 1 m •1000 m = 1 km Imperial •12 inches = 1 foot •36 inches or 3 feet = 1 yard •5280 feet or 1760 yards = 1 mile
- 21. Unit Conversion Unit ConversionRatio To convert a measurement given in one unit of measure to another unit of measure, a unit conversion ratio can be used. A unit conversion ratio is a fraction equal to 1.
- 22. Unit Conversion Unit ConversionRatio Examples of unit conversion ratios taken from the table on the previous slide are: The conversion factor can be written with either value in the numerator or the denominator. For example:
- 23. Unit Conversion Unit ConversionRatio When converting between units of measure, it is best to write the conversion factor as follows: • The numerator of the ratio consists of the required unit of measure (the unit to which you want to convert). • The denominator of the ratio consists of the given unit of measure (the original units in which the measurement was taken).
- 24. Unit Conversion Example 1 You purchase 485 cm of wire, however it is sold by the meter. How many meters of wire must you purchase?
- 25. Unit Conversion Example 2 A plank measures 6 ft, 4 in. How many inches long is the plank?
- 26. Unit Conversion Example 3 A living room has a length of 5 yards, 2 feet. What is the length of the room in inches?
- 27. Unit Conversion Example 4 Perform the following calculation: 2 km – 820 m = _______
- 28. Unit Conversion Notebook Assignment Page 213 - 214 Q. 1 - 8
- 29.
- 30.
- 31.
- 32. Unit Conversion Example 1 Convert 70 miles per hour into km/h.
- 33. Unit Conversion Example 2 Your dining room measures 5 m x 8 m. How many square yards is this?
- 34. Unit Conversion Notebook Assignment Page 218 Q. 1 - 5
- 35. Surface Area • Whatdoes it mean to you? • Surface area is found by finding the area of all the sides and then adding those answers up. • How will the answer be labeled? • Units2 because it is area!
- 36. Definition Surface Area –is the total number of unit squares used to cover a 3-D surface.
- 37. Find the SAof a Rectangular Solid A rectangular solid has 6 faces. Top They are: Top Bottom Front Right Back Side Front Right Side Left Side We can only see 3 faces at any one time. Which of the 6 sides are the same? Top and Bottom Front and Back Right Side and Left Side
- 38. Surface Area ofa Rectangular Solid We know that Each face is a rectangle. Top and the Formula for finding the area of a Right rectangle is: Side A = lw Front Steps: Find: Area of Top Area of Front Area of Right Side Find the sum of the areas Multiply the sum by 2. The answer you get is the surface area of the rectangular solid.
- 39. Find the SurfaceArea of the following: Find the Area of each face: 12 m 2 Top 5m A = 12 m x 5 m = 60 m Top Right Side 8m Front Front 8m A = 12 m x 8 m = 96 m 2 5m 12 m 12 m 2 2 2 2 Sum = 60 m + 96 m + 40 m = 196 m Right 2 Side 8m A = 8 m x 5 m = 40 m 2 2 Multiply sum by 2 = 196 m x 2 = 392 m 5m 2 The surface area = 392 m
- 40. Find the SurfaceArea Area of Top = 6 cm x 4 cm = 24 2 cm 2 24 m 2 Area of Front = 14 cm x 6 cm = 84 cm 2 Area of Right Side = 14 cm x 4 cm = 56 cm 2 2 56 m Find the sum of the areas: 14 cm 84 m 2 2 2 2 24 cm + 84 cm + 56 cm = 164 cm Multiply the sum by 2: 4 cm 2 2 6 cm 164 cm x 2 = 328 cm The surface area of this 2 rectangular solid is 328 cm .
- 41. Nets A net isall the surfaces of a rectangular solid laid out flat. Back 8 cm Top Left Side Top Right Side 5 cm Right 8 cm Side Front 8 cm Front 8 cm 5 cm 10 cm 5 cm Bottom 10 cm
- 42. Find the SurfaceArea using nets. Top Back 8 cm Right Side Front 8 cm Left Side Top Right Side 5 cm 5 cm 8 cm 10 cm Front 8 cm Each surface is a rectangle. 80 A = lw 80 5 cm Find the area of each surface. Bottom Which surfaces are the same? 10 cm 40 Find the Total Surface Area. 50 50 40 What is the Surface Area of the Rectangular solid? 2 340 cm
- 43. VOLUME AND CAPACITY Essential Math 30S
- 44. Problem of theDay How can you cut the rectangular prism into 8 pieces of equal volume by making only 3 straight cuts?
- 45. Problem of theDay How can you cut the rectangular prism into 8 pieces of equal volume by making only 3 straight cuts?
- 46. What is volumeand capacity? Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains. The volume of a container is generally understood to be the capacity of the container, that is the amount of fluid that the container could hold.
- 48. Warm Up Identify thefigure described. 1. two triangular faces and the other faces in the shape of a parallelograms 2. one hexagonal base and the other faces in the shape of triangles 3. one circular face and a curved lateral surface that forms a vertex
- 49. Warm Up Identify thefigure described. 1. two triangular faces and the other faces in the shape of a parallelograms triangular prism 2. one hexagonal base and the other faces in the shape of triangles hexagonal pyramid 3. one circular face and a curved lateral surface that forms a vertex cone
- 50. Volume: Prisms, Cylinders,Pyramids, and Cones
- 51. Volume of aPrism h V Bh Volume Base Area Height Base Area Remember the “Base Area” formula will be determined by the base shape.
- 52. Example #1: Findingthe Volume of a Prism Find the volume of the regular rectangular prism. V Bh B (4)(12) V (48)(12) 3 V 576 ft
- 53. Volume of aCylinder Base Area Radius V Bh Volume Base Area Height h 2 B r Base Radius Area
- 54. Example #2 Findingthe Volume of a Cylinder Find the volume of a cylinder with height 10 cm 5 cm and radius 5cm. V Bh 10 cm 2 B r 2 B (5) 2 B 25 cm V 25 (10) 3 V 250 cm
- 55. Volume of aPyramid 1 V Bh B Volume 3 Base Area Height
- 56. Example #3 FindingVolume of a Pyramid Find the volume of a square pyramid with base edges 5 m and height 3 m. 1 3m V Bh 3 B s2 B 52 2 5m B 25 m 1 V (25)(3) 3 3 V 25 m
- 57. Volume of aCone 1 V Bh Volume 3 Height Base Area r B
- 58. Example#4 Finding the Volume of a Cone The radius of the base of a cone is 6 m. Its height is 13 m. Find the volume. 1 V Bh 3 13 m B r2 2 B 6 B 36 m 2 6m 1 V (36 )(13) 3 3 V 156 m
- 59. Practice Assignment Worksheet 4.1 Practice Questions 1-7, Pages 90-91
- 60. A sphere isa 3D figure that is circular in shape, e.g., a ball. All points on the sphere are equidistant from a single point inside the sphere called the centre.
- 61. Volume of aSphere SUMMARIZING: Volume (cylinder) = (Area Base) (height) Volume (cone) = Volume (cylinder) /3 = 3 Volume (cone) = (Area Base) (height)/3 AND 2(Volume (cone)) = Volume (sphere) 2X =
- 62. Volume of aSphere 2(Volume (cone)) = Volume (sphere) 2X = 2(Area of Base ) (height) /3= Volume (sphere) 2( r2 )(h)/3= Volume (sphere) r h BUT h = 2r r 2( r2)(2r)/3 = Volume(sphere) 4( r3)/3 = Volume(sphere)
- 63. Volume of aSphere 3 4 r Volume sphere 3 4 r 3 3
- 64. Find the volumeand surface area of a sphere with radius 12 cm. Volume = (4/3)πr3
Editor's Notes
- #2 This template can be used as a starter file for presenting training materials in a group setting.SectionsRight-click on a slide to add sections. Sections can help to organize your slides or facilitate collaboration between multiple authors.NotesUse the Notes section for delivery notes or to provide additional details for the audience. View these notes in Presentation View during your presentation. Keep in mind the font size (important for accessibility, visibility, videotaping, and online production)Coordinated colors Pay particular attention to the graphs, charts, and text boxes. Consider that attendees will print in black and white or grayscale. Run a test print to make sure your colors work when printed in pure black and white and grayscale.Graphics, tables, and graphsKeep it simple: If possible, use consistent, non-distracting styles and colors.Label all graphs and tables.
- #3 Give a brief overview of the presentation. Describe the major focus of the presentation and why it is important.Introduce each of the major topics.To provide a road map for the audience, you can repeat this Overview slide throughout the presentation, highlighting the particular topic you will discuss next.
- #4 Give a brief overview of the presentation. Describe the major focus of the presentation and why it is important.Introduce each of the major topics.To provide a road map for the audience, you can repeat this Overview slide throughout the presentation, highlighting the particular topic you will discuss next.
- #5 Give a brief overview of the presentation. Describe the major focus of the presentation and why it is important.Introduce each of the major topics.To provide a road map for the audience, you can repeat this Overview slide throughout the presentation, highlighting the particular topic you will discuss next.
- #44 This template can be used as a starter file for presenting training materials in a group setting.SectionsRight-click on a slide to add sections. Sections can help to organize your slides or facilitate collaboration between multiple authors.NotesUse the Notes section for delivery notes or to provide additional details for the audience. View these notes in Presentation View during your presentation. Keep in mind the font size (important for accessibility, visibility, videotaping, and online production)Coordinated colors Pay particular attention to the graphs, charts, and text boxes. Consider that attendees will print in black and white or grayscale. Run a test print to make sure your colors work when printed in pure black and white and grayscale.Graphics, tables, and graphsKeep it simple: If possible, use consistent, non-distracting styles and colors.Label all graphs and tables.
- #47 Give a brief overview of the presentation. Describe the major focus of the presentation and why it is important.Introduce each of the major topics.To provide a road map for the audience, you can repeat this Overview slide throughout the presentation, highlighting the particular topic you will discuss next.
- #48 This is another option for an Overview slides using transitions.
- #51 Give a brief overview of the presentation. Describe the major focus of the presentation and why it is important.Introduce each of the major topics.To provide a road map for the audience, you can repeat this Overview slide throughout the presentation, highlighting the particular topic you will discuss next.