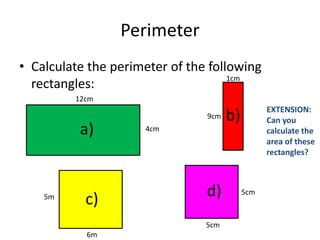
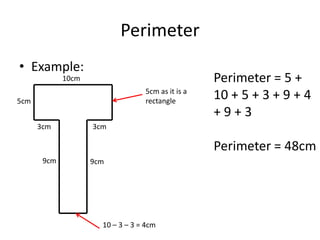
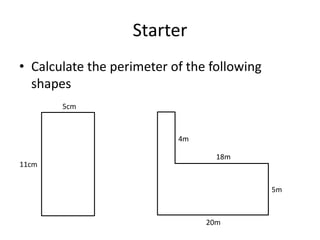
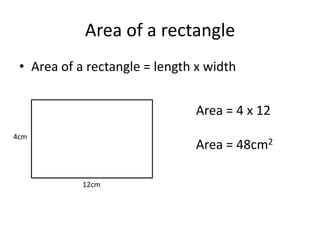
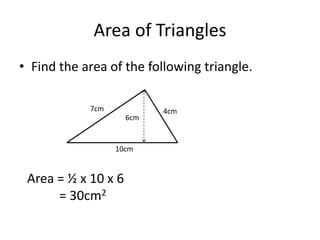
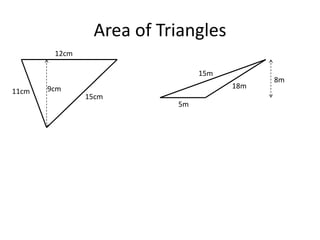
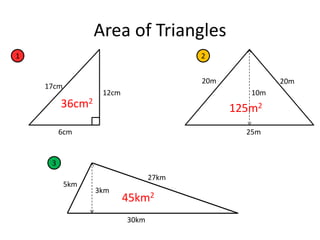
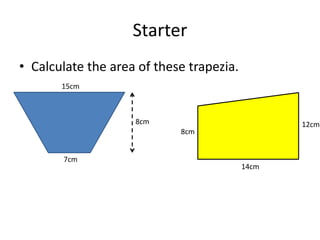
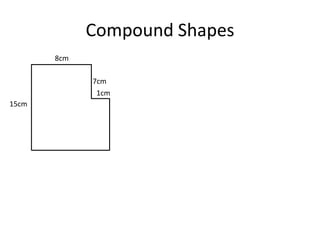
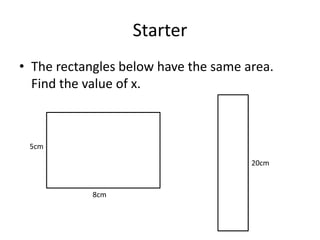
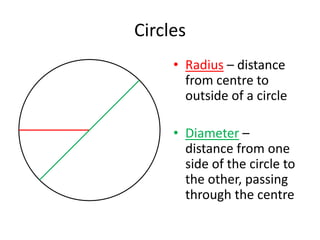
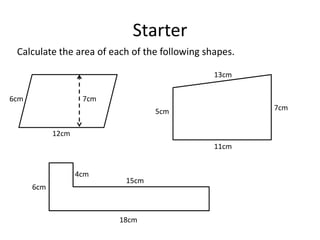
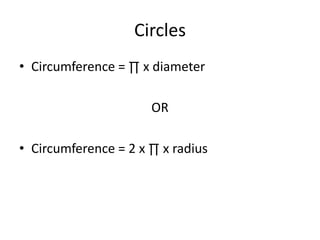
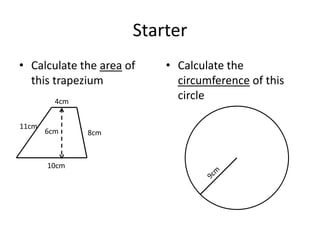
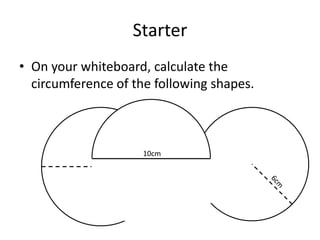
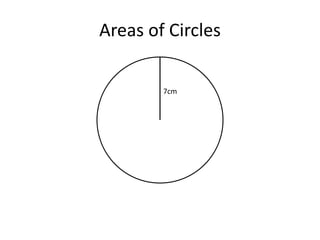
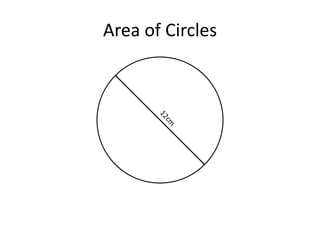
Here are the steps to solve these circle area problems: 1) Be given the radius or diameter 2) Use the formulas: - Area = πr^2 (given radius) - Diameter = 2r, so radius = diameter/2 (given diameter) 3) Plug the values into the appropriate formula 4) Simplify and calculate 5) Round to the correct number of decimal places Show your work and write the final answer with units (cm^2). Let me know if any specific problem gives you trouble!

1. Starter
• On whiteboards, write down as many units of
LENGTH as you can
• Write down as many units for AREA as you can
EXTENSION:
What is the perimeter of
this rectangle?

2. Perimeter 25/02/2013
Learning Objectives:
Know the key words for perimeter and
the units used
Able to calculate the perimeter of a
rectangle
Able to calculate the perimeter of a
compound shape

3. Perimeter
• Perimeter: The distance around the outside of
a shape
• To calculate the perimeter, you add together
all the sides of a shape

4. Perimeter
10cm
• Example:
3cm
P = 10 + 3 + 10 + 3
P = 26cm

5. Perimeter
• Calculate the perimeter of the following
1cm
rectangles:
12cm
EXTENSION:
9cm b) Can you
a) 4cm calculate the
area of these
rectangles?
5m
c) d) 5cm
5cm
6m

6. Perimeter
• Compound shape: a 2D shape made up of
many shapes

7. Perimeter
10m Can I calculate the
perimeter of this
shape?
15m
I need to find the
21m length of the
25m
missing sides first.
P = 10 + 15 + 21 + 10 + 31 + 25
10m Now I can calculate
P = 112m the perimeter by
adding up the all the
31m sides.

8. Perimeter
• Example:
10cm Perimeter = 5 +
5cm as it is a
5cm rectangle
10 + 5 + 3 + 9 + 4
+9+3
3cm 3cm
Perimeter = 48cm
9cm 9cm
10 – 3 – 3 = 4cm

9. Starter
• Calculate the perimeter of the following
shapes
5cm
4m
18m
11cm
5m
20m

10. Perimeter 25/02/2013
Learning Objectives:
Able to calculate the perimeter of a
rectangle
Able to calculate the perimeter of a
compound shape
Able to calculate the area of a
rectangle

11. Your turn…
• Exercise 5A, page 97

12. Area
• How can I calculate the area of this rectangle?
• Count the squares
inside the shape
• Multiply the width
by the length

13. Area of a rectangle
• Area of a rectangle = length x width
Area = 4 x 12
4cm
Area = 48cm2
12cm

14. Starter
• How many rectangles can you design that
have an area of 24cm2?
• Do the sides have to be whole numbers?

15. Area of Triangles 25/02/2013
Learning Objectives:
• Able to calculate the area of a rectangle
• Able to calculate the area of a triangle
• Able to calculate the area of a compound
shape

16. Area of Triangles
Height
Base
• Area of a triangle = ½ x base x height
= ½bh

17. Area of a Triangle
• Calculate the area of this triangle.
4cm
12cm
Area = ½ x 4 x 12
= 24cm2

18. Area of Triangles
• Find the area of the shaded triangle BCD.
5cm 4cm
A B C
6cm
Area of ACD = ½ x 9 x 6
= 27cm2
11cm
Area of ABD = ½ x 5 x 6
D = 15cm2
Area of BCD = 27 – 15
= 12cm2

19. Your turn…
• Page 104, Exercise 5E, Qs 1 to 4.

20. Starter
• Complete the worksheet in your workbook
– Show all your working out
– Remember to use the correct units!

21. Grade D
Area of Triangles 25/02/2013
Learning Objectives:
• Able to calculate the area of a right angled
triangle
• Able to identify the perpendicular height of a
triangle
• Able to calculate the area of any triangle

22. Area of Triangles
• Perpendicular – “at right angles to”

23. Area of Triangles
The perpendicular
height
• Area = base x height
2
base
height height
height
base
base

24. Area of Triangles
• Find the area of the following triangle.
7cm 4cm
6cm
10cm
Area = ½ x 10 x 6
= 30cm2

25. Area of Triangles
12cm
15m
8m
9cm 18m
11cm
15cm
5m

26. Grade D
Area of Triangles 25/02/2013
Learning Objectives:
• Able to calculate the area of a right-angled
triangle
• Able to calculate the area of other
triangles
• Able to calculate the area of a parallelogram

27. Area of Triangles
1 2
20m 20m
17cm
12cm 10m
36cm2 125m2
6cm 25m
3
27km
5km
3km
45km2
30km

28. Some work…
• In your workbooks, work through pages 65
and 66.

29. Home Learning
• Complete the worksheet in your books
• Show all working out
• DUE: Monday 19th September

30. Starter
• Match the shape to the correct area and
perimeter.
• There is one perimeter and one area that
don’t have a shape. Draw the shape to match
the perimeter and area on the blank card.

31. Parallelograms and Trapezia
Grade D 25/02/2013
Learning Objectives
• Able to calculate the area of triangles
• Able to calculate the area of parallelograms
and trapezia

32. Area of a Parallelogram
Area of Parallelogram = base x perpendicular
height
height
Base
Area = 6 x 12
9cm
6cm
= 72cm2
12cm

33. Area of a Trapezium
a
h
b
Area of Trapezium = ½ (a + b) x h
a and b are the parallel sides

34. Starter
• Calculate the area of these trapezia.
15cm
8cm 12cm
8cm
7cm
14cm

35. Area of Compound Shapes
Grade D 25/02/2013
Learning Objectives:
• Able to calculate areas of trapezia
• Able to split up a compound shape
• Able to find the area of a compound
shape

36. Compound Shapes
• To find the area of compound shapes, split
them up into their composite shapes.
• Find the area of each shape, then add them
together

37. Compound Shapes
8cm
Area A = 8 x 5
A 5cm
= 40cm2
Area B = 11 x 2
= 22cm2
B 11cm
Total Area = 40 + 22
= 62cm2
2cm

38. Compound Shapes
8cm
7cm
1cm
15cm

39. Your turn…
• Complete the worksheet in your work books.

40. Starter
• The rectangles below have the same area.
Find the value of x.
5cm
20cm
8cm

41. Grade D/C
Circles 25/02/2013
Learning Objectives:
• Able to calculate the radius and diameter
of a circle
• Able to use a calculator to find the
circumference of a circle
• Able to calculate the area of a circle

42. Circles
• Radius – distance
from centre to
outside of a circle
• Diameter –
distance from one
side of the circle to
the other, passing
through the centre

43. Circles
Diameter = 2 x radius
Radius = diameter ÷ 2
6cm 12cm 6cm

44. Circles
• Circumference – the distance around the
outside of a circle.
• You are going to investigate the relationship
between the circumference and the diameter.

45. Circles
1) Measure the circumference and diameter of
the objects and record them in the table.
2) Divide the circumference by the diameter.
Write your results in the table
3) Can you spot the common link?

46. Object Circumference Diameter C÷d

47. Starter
Calculate the area of each of the following shapes.
13cm
6cm 7cm
5cm 7cm
12cm
11cm
4cm
15cm
6cm
18cm

48. Grade D/C
Circles 25/02/2013
Learning Objectives:
• Able to calculate the radius and diameter
of a circle
• Able to use a calculator to find the
circumference of a circle
• Able to calculate the area of a circle

49. Circles
• This relationship between the circumference and
diameter is called ‘pi’
• The symbol for pi is ∏
• ∏ = 3.1415926….
• We often use 3.14 as an approximation
• It is found on calculators

50. Circles
• Circumference = ∏ x diameter
OR
• Circumference = 2 x ∏ x radius

51. Circles
Circumference = 2∏r
C=2x∏x4
4cm
C=8x∏
C = 25.13cm (2dp)

52. Circles
Find the circumference of the
circle.
7cm
C=2x∏x7
C = 14 x ∏
C = 43.98cm (2dp)

53. Starter
• Calculate the area of • Calculate the
this trapezium circumference of this
4cm
circle
11cm
6cm 8cm
10cm

54. Grade D/C
Circumference 25/02/2013
Learning Objectives:
• Able to calculate the radius and diameter
of a circle
• Able to use a calculator to find the
circumference of a circle
• Able to calculate the area of a circle

55. Circles
If I want to find the circumference of these circles, which formula
should I use?
6cm
C=2x∏xr C=∏xd
C=2x∏x6 C = ∏ x 14
C = 12 x ∏ C = 43.98 (2dp)
C = 37.7cm (1dp)

56. Circles
• Page
– Exercise
– Questions

57. Starter
• On your whiteboard, calculate the
circumference of the following shapes.
10cm
9cm

58. Grade C
Area of Circles 25/02/2013
Learning Objectives:
• Able to calculate the circumference of a circle
• Able to calculate the area of a circle given
the radius
• Able to calculate the area of a circle given
the diameter

59. Area of Circles
• Area = ∏ x radius2
• Area = ∏r2
radius

60. Area of Circles
• Area = ∏r2
• Area = ∏ x 42
• Area = ∏ x 4 x 4 4cm
• Area = 16 x ∏
• Area = 50.27cm2

61. Areas of Circles
7cm

62. Area of Circles
• Radius = 18 ÷ 2
= 9cm
• Area = ∏ x 92 18cm
• Area = 81 x ∏
• Area = 254.47cm2

63. Area of Circles

64. Your turn…
• Page 364 – 366
– Exercise 16C
– Questions 1, 3, 5, 6, 7*, 9*