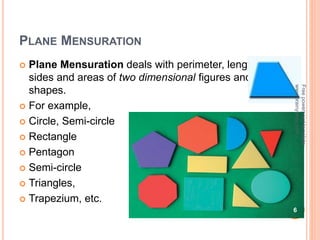
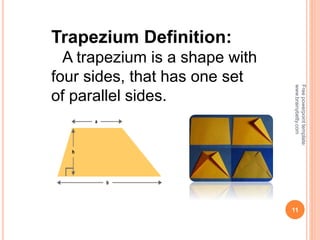
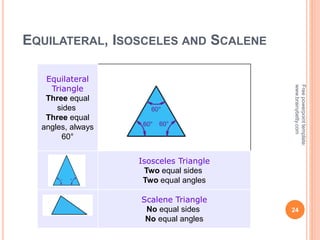
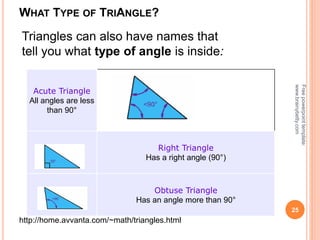
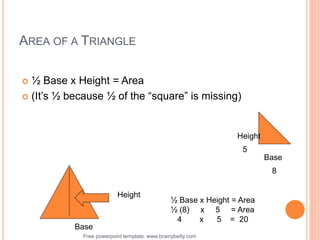
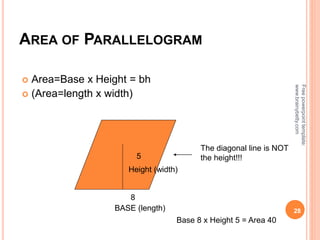
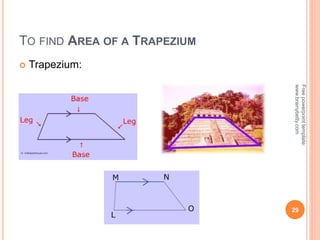
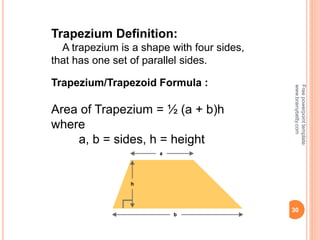
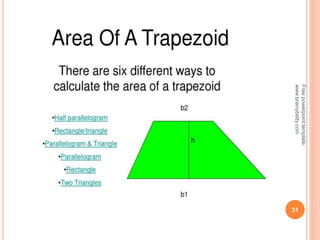
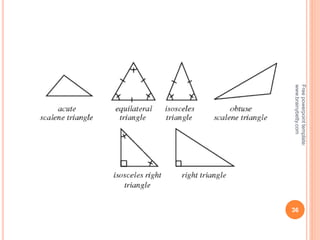
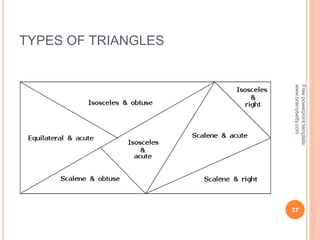
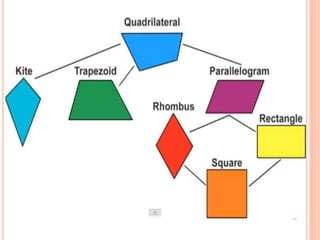
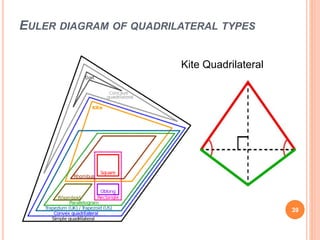
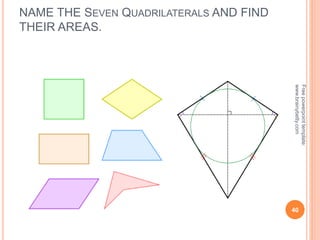
This document discusses the topic of mensuration, which is the measurement of quantities such as perimeter, area, volume, and length of geometrical figures. It begins by explaining that mensuration is important for tasks like building houses or planning gardens, as it allows one to calculate the space occupied by different shapes. The document then provides definitions and examples of plane mensuration, which deals with 2D figures, and solid mensuration, which involves 3D solids. Specific shapes discussed include triangles, rectangles, circles, cylinders, cones, and spheres. Formulas are presented for calculating the areas of common shapes like triangles, rectangles, parallelograms, and trapezoids.

1. MENSURATION
MATH-103
Mathematics for Interior Design
Dr. Farhana Shaheen

2. MENSURATION
 Mensuration is to measure the quantities such as
perimeter, area, volume, length of a closed
geometrical figure.
 If we want to build a house or planning a garden,
we need to know exactly the space we have and
the amount of space we need. For the purpose for
these we have to calculate the length of the
boundary and space occupied.
 In other words we have to determine the perimeter
and area of the plot.
2
Free
powerpoint
template:
www.brainybetty.com

3. 3
Free
powerpoint
template:
www.brainybetty.com

4. DEFINITION: MENSURATION
 Mensuration is a branch of Mathematics which
deals with the measurements of lengths of lines,
areas of surfaces and volumes of solids.
 Mensuration may be divided into two parts:
 1. Plane Mensuration (for 2 dimension)
 2. Solid Mensuration (for 3 dimension)
4
Free
powerpoint
template:
www.brainybetty.com

5. SHAPES IN 2-D
AND 3-D

6. PLANE MENSURATION
 Plane Mensuration deals with perimeter, length of
sides and areas of two dimensional figures and
shapes.
 For example,
 Circle, Semi-circle
 Rectangle
 Pentagon
 Semi-circle
 Triangles,
 Trapezium, etc.
6
Free
powerpoint
template:
www.brainybetty.com

7. SOLID MENSURATION
 Solid mensuration deals with areas and volumes of
solid objects in three dimensions.
 For example: Polyhedrons, Cylinders, Cones,
Spheres. They are called Space Figures.
7
Free
powerpoint
template:
www.brainybetty.com

8. SPACE FIGURES
 Polyhedrons are space figures with flat surfaces, called faces,
which are made of polygons.
 Prisms and pyramids are examples of polyhedrons.
 A cylinder has two parallel, congruent bases that are circles.
 A cone has one circular base and a vertex that is
not on the base.
 A sphere is a space figure having all its points an equal
distance from the center point.
Note that cylinders, cones, and spheres are not polyhedrons,
because they have curved, not flat, surfaces.

9. EXAMPLES OF POLYHEDRONS
9
Free
powerpoint
template:
www.brainybetty.com

10. Here is an interesting and
lovely way to look at the
beauty of mathematics, and of
God, the sum of all wonders.
The Beauty of
Mathematics
Shapes of Numbers
Wonderful World
10
Free
powerpoint
template:
www.brainybetty.com

11. 11
Trapezium Definition:
A trapezium is a shape with
four sides, that has one set
of parallel sides.
Free
powerpoint
template:
www.brainybetty.com

12. 1 x 8 + 1 = 9
12 x 8 + 2 = 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 98765
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543
12345678 x 8 + 8 = 98765432
123456789 x 8 + 9 = 98765432112
Free
powerpoint
template:
www.brainybetty.com

13. 1 x 9 + 2 = 11
12 x 9 + 3 = 111
123 x 9 + 4 = 1111
1234 x 9 + 5 = 11111
12345 x 9 + 6 = 111111
123456 x 9 + 7 = 1111111
1234567 x 9 + 8 = 11111111
12345678 x 9 + 9 = 111111111
123456789 x 9 +10= 1111111111 13
Free
powerpoint
template:
www.brainybetty.com

14. 9 x 9 + 7 = 88
98 x 9 + 6 = 888
987 x 9 + 5 = 8888
9876 x 9 + 4 = 88888
98765 x 9 + 3 = 888888
987654 x 9 + 2 = 8888888
9876543 x 9 + 1 = 88888888
98765432 x 9 + 0 = 888888888
Brilliant, isn’t it? 14
Free
powerpoint
template:
www.brainybetty.com

15.  0 x 9 + 8 = 8
9 x 9 + 7 = 88
98 x 9 + 6 = 888
987 x 9 + 5 = 8888
9876 x 9 + 4 = 88888
98765 x 9 + 3 = 888888
987654 x 9 + 2 = 8888888
9876543 x 9 + 1 = 88888888
98765432 x 9 + 0 = 888888888
987654321 x 9 - 1 = 8888888888
9876543210 x 9 - 2 = 88888888888
15
Free
powerpoint
template:
www.brainybetty.com

16. 1 x 1 = 1
11 x 11 = 121
111 x 111 = 12321
1111 x 1111 = 1234321
11111 x 11111 = 123454321
111111 x 111111 = 12345654321
1111111 x 1111111 = 1234567654321
11111111 x 11111111 = 123456787654321
111111111 x 111111111 =
12345678987654321
And look at this symmetry:
16
Free
powerpoint
template:
www.brainybetty.com

17. TAKE A LOOK AT THIS SYMMETRY:
RIGHT ANGLED TRIANGLE
 1 x 1 = 1
11 x 11 = 121
111 x 111 = 12321
1111 x 1111 = 1234321
11111 x 11111 = 123454321
111111 x 111111 = 12345654321
1111111 x 1111111 = 1234567654321
11111111 x 11111111 = 123456787654321
111111111 x 111111111 = 12345678987654321
17
Free
powerpoint
template:
www.brainybetty.com

18. PLANE MENSURATION
18
Free
powerpoint
template:
www.brainybetty.com

19. AREA OF CLOSED FIGURES
 The measure of region enclosed in a closed figure
is called Area.
 For example, we need to find the areas of
Polygons, Circles, or any other closed figures.
 http://www.helpingwithmath.com/by_subject/geomet
ry/geo_area.htm 19
Free
powerpoint
template:
www.brainybetty.com

20. TANGRAMS
20
Free
powerpoint
template:
www.brainybetty.com

21. CONCEPT OF AREA AND ITS USES IN DAILY
LIFE SITUATIONS
 There are two vacant rooms in a school numbered as 3
and 4. Students of class-VI are to take their mid-day
meals. The monitor was asked to make arrangements
for the students of his class in room number 3. He said
“Students of our class cannot be accommodated in
Room No.3, but they can be accommodated in Room
No. 4”. What could be the difference between the two
rooms so that one of these can accommodated the
students of Class VI whereas the other one cannot
accommodate it? The general answer will be Room No.
4 is bigger than Room No. 3. It is because the region
enclosed within Room No. 4 is greater than Room No. 3.
Thus, the measure of region enclosed in a closed
figure is called Area.
http://www.helpingwithmath.com/by_subject/geometry/g
eo_area.htm
21
Free
powerpoint
template:
www.brainybetty.com

22. UNIT OF MEASUREMENT OF AREA
 To measure anything we first fix a unit to be used to
measure it such as:
 To measure a length, you use a meter as a unit.
 Area is measured in square unit like 3 m or 5 cm .
TABLE FOR AREA
NAME AREA
 Rectangle Length*breadth = L W
 Square Side*Side = s
 Triangle 1/2 Base*Altitude = ½ b h
 Parallelogram Base*Altitude = b h
 Trapezium 1/2*h (Sum of two parallel side) = ½ h (a + b)
2 2
22
2
Free
powerpoint
template:
www.brainybetty.com

23. TRIANGLES
 A triangle has three sides and three angles.
 The three angles always add to 180°
 There are three special names given to triangles
that tell how many sides (or angles) are equal.
There can be 3, 2 or no equal sides/angles:
 Equilateral Triangle has all 3 sides equal
 Isosceles Triangle has 2 sides equal
 Scalene Triangle has No sides equal
23
Free
powerpoint
template:
www.brainybetty.com

24. EQUILATERAL, ISOSCELES AND SCALENE
Equilateral
Triangle
Three equal
sides
Three equal
angles, always
60°
Isosceles Triangle
Two equal sides
Two equal angles
Scalene Triangle
No equal sides
No equal angles
24
Free
powerpoint
template:
www.brainybetty.com

25. WHAT TYPE OF TRIANGLE?
Acute Triangle
All angles are less
than 90°
Right Triangle
Has a right angle (90°)
Obtuse Triangle
Has an angle more than 90°
25
Triangles can also have names that
tell you what type of angle is inside:
Free
powerpoint
template:
www.brainybetty.com
http://home.avvanta.com/~math/triangles.html

26. EXAMPLE: TO FIND AREA OF A TRIANGLE
 To find the area of the Triangle we should know the
base and altitude(height)
 Area of the triangle=1/2*base*altitude
Exp:1
Find the area of the triangle which base is 6 m and
altitude is 8 m?
 Solution: Here, Base of the triangle= 6 m
Altitude of the triangle = 8 m
Area of the Triangle= 1/2*base*altitude
= 1/2*6*8 = 24 m2
26
Free
powerpoint
template:
www.brainybetty.com

27. Free powerpoint template: www.brainybetty.com 27
AREA OF A TRIANGLE
 ½ Base x Height = Area
 (It’s ½ because ½ of the “square” is missing)
Base
Height
Height
Base
8
5
½ Base x Height = Area
½ (8) x 5 = Area
4 x 5 = 20

28. 28
AREA OF PARALLELOGRAM
 Area=Base x Height = bh
 (Area=length x width)
BASE (length)
Height (width)
8
5
Base 8 x Height 5 = Area 40
The diagonal line is NOT
the height!!!
Free
powerpoint
template:
www.brainybetty.com

29. TO FIND AREA OF A TRAPEZIUM
 Trapezium:
29
Free
powerpoint
template:
www.brainybetty.com

30. 30
Trapezium Definition:
A trapezium is a shape with four sides,
that has one set of parallel sides.
Trapezium/Trapezoid Formula :
Area of Trapezium = ½ (a + b)h
where
a, b = sides, h = height
Free
powerpoint
template:
www.brainybetty.com

31. 31
Free
powerpoint
template:
www.brainybetty.com

32. EXAMPLE: TO FIND AREA OF A
TRAPEZIUM
 To find the area of the Trapezium, we should know
the altitude(height)and sides
 Ques: Find the area of the Trapezium which height
is 4 m and sides are 10 m and 12 m?
 Solution: Here, height of the Trapezium=h= 4 m
Side of one Trapezium= a = 10 m
Side of another Trapezium= b = 12 m
Area of the Triangle = 1/2*h(a + b)
=1/2*4(10+12) = 44 m2
32
Free
powerpoint
template:
www.brainybetty.com

33. Free powerpoint template: www.brainybetty.com 33
DIFFERENT NAMES/SAME IDEA
 Length x Width = Area
 Side x Side = Area
 Base x Height = Area

34. QUESTION: FIND THE AREA OF THE GIVEN
SCALENE TRIANGLE
34
Free
powerpoint
template:
www.brainybetty.com
Example: What is the area of this triangle?
Height = h = 12
Base = b = 20
Area = ½ × b × h = ½ × 20 × 12 = 120
Note: The base can be any side, Just be
sure the "height" is measured at right
angles to the "base“.

35.  Can you find the Areas of these closed figures?
35
Free
powerpoint
template:
www.brainybetty.com

36. 36
Free
powerpoint
template:
www.brainybetty.com

37. TYPES OF TRIANGLES
37
Free
powerpoint
template:
www.brainybetty.com

38. 38
Free
powerpoint
template:
www.brainybetty.com

39. EULER DIAGRAM OF QUADRILATERAL TYPES
Kite Quadrilateral
39

40. NAME THE SEVEN QUADRILATERALS AND FIND
THEIR AREAS.
40
Free
powerpoint
template:
www.brainybetty.com

41. QUICK CHECK:
 i. The sum of all angles in a triangle is
___________ degrees.

 ii. The area of a triangle is
__________________________

 iii. The area of a trapezium is
______________________

 iv. _____________ triangle has two sides equal.
41
Free
powerpoint
template:
www.brainybetty.com

42. QUICK CHECK:
o v. _______________triangle has one 90 degree
angle
o vi. _______________ triangle has all angles and
sides are the same.
 vii. ________________ triangle: Has all three
angles and all three sides different.
 viii. The interior angles of a simple
quadrilateral ABCD add up to
______ degrees.
42