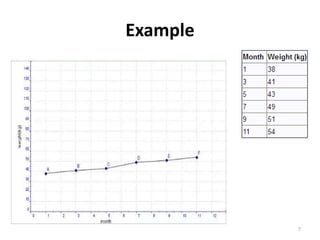
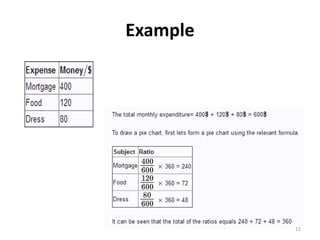
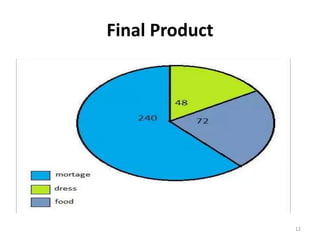
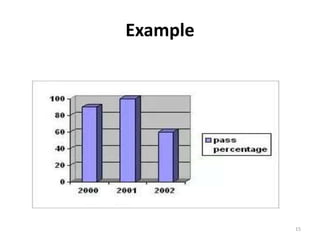
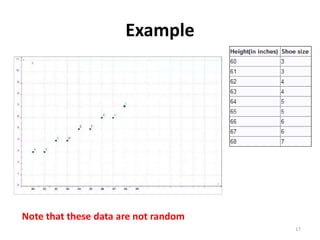
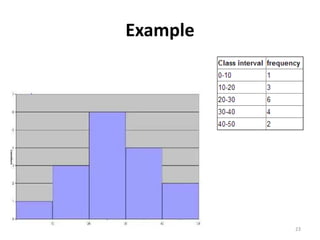
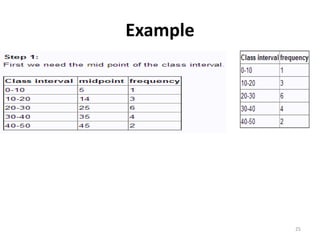
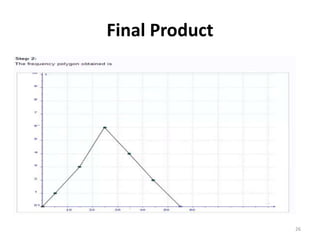
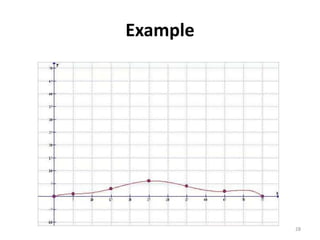
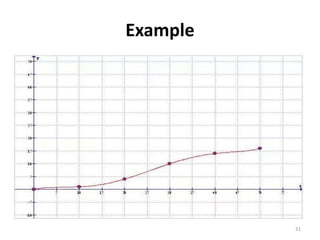
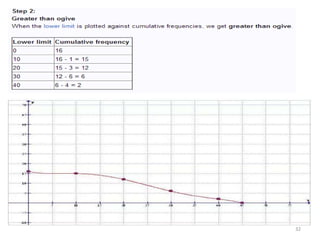
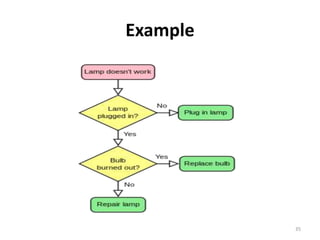
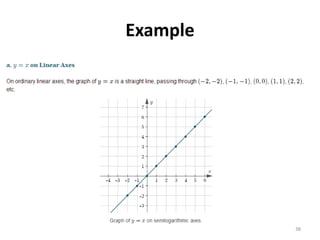
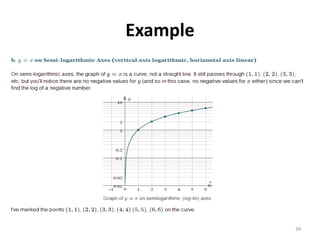
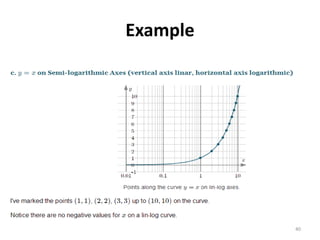
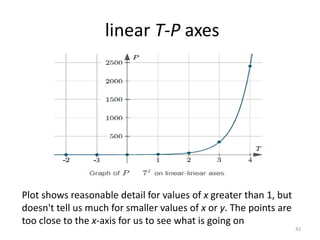
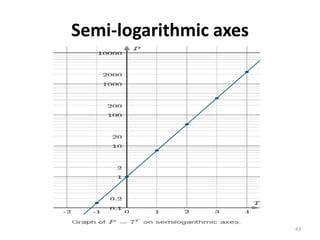
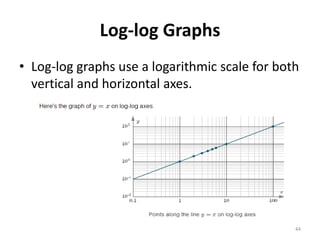
The document discusses various types of graphs and flow charts for statistical data representation, including line graphs, pie charts, bar graphs, and histograms. It explains their uses, advantages, and limitations while also introducing flow charts to illustrate process sequences. Additionally, it covers logarithmic graphing techniques, emphasizing the importance of visualizing data effectively.

1. TYPES OF GRAPH AND FLOW
CHART
By M. Waleed Ahsan Khan Tareen
13-arid-1100
DVM 8th evening

2. Contents
• Prelude
• PART (A) TYPES OF GRAPHS
• PART (B) FLOW CHART
• PART (C) LOG AND SEMI LOG GRAPH
2

3. Statistics
• Numbers that is concerned with collection,
organization, measurement, and analysis of
the numerical data.
• The graphical demonstration of statistical data
in a chart is normally specified as statistical
graph chart.
3

4. WHY GRAPHS ?
• To reveal a trend or comparison of a data
• Easily understood
4

5. (A)Types
There are different kinds of graphical charts based on
statistics as follows:
1. Line graphs
2. Pie charts
3. Bar graph
4. Scatter plot
5. Stem and plot
6. Histogram
7. Frequency polygon
8. Frequency curve
9. Cumulative frequency or ogives
5

6. Line Graph
• A line joining several points, or a line that
shows the relationship between the points
• xy plane
• independent variable and a dependent
variable
6

7. Example
7

8. Pie Charts
• A pie chart can be taken as a circular graph
which is divided into different disjoint pieces,
each displaying the size of some related
information.
• Represents a whole and each part represents
a percentage of the whole
8

9. Advantages
• Good visual treat
• Percentage value-instantly known
9

10. Preferred use(Limitation)
• Categorical data - one understand what
percentage each of these category constitute
10

11. Example
11

12. Final Product
12

13. Bar Graph
• Bar graph is drawn on an x-y graph and it has
labelled horizontal or vertical bars that show
different values
• The size, length and color of the bars
represent different values.
13

14. Preferred use(Limitation)
• Non continuous data
• Comparing or contrasting the size of the
different categories of the data provided.
14

15. Example
15

16. Scatter plot
• A scatter plot or scatter graph is a type of graph
which is drawn in Cartesian coordinate to visually
represent the values for two variables for a set of
data. It is a graphical representation that shows
how one variable is affected by the other.
• Data is presented-collection of points-value of a
variable positioned horizontal or x-axis
(Explanatory variable )
• Value of the other variable positioned on the
vertical or y-axis(response variable)
16

17. Example
Note that these data are not random
17

18. Stem and Leaf Plot
• Stem and leaf plot also called as stem plot are
connected with quantitative data such that it
helps in
• Displaying shapes of the distributions,
• Organize numbers and
• Set it as comprehensible as possible.
18

19. Stem and leaf
• Descriptive technique-emphases on the data provided
• It concludes more about the shape of a set of data
• Provides better view about each of the data. The data
is arranged by “place value”.
• In Stem plots each data is taken divide  Two
separate parts  a stem and a leaf.
• A stem is usually the first digit of the number in the
data a vertical column
• a leaf is the last digit of the number in the data the
row to the right side of the corresponding stem
19

20. Example
20

21. 21

22. Histogram
• Histogram is the most accurate graph that represents a
frequency distribution.
• In the histogram the scores are spread uniformly over
the entire class interval.
• The class intervals are plotted on the x-axis and the
frequencies on the y-axis. Each interval is represented
by a separate rectangle.
• The area of each rectangle is proportional to the
number of measures within the class- interval. The
entire histogram is proportional to the statistical data
set.
22

23. Example
23

24. Frequency Polygon
• The frequency polygon has most of the properties of a
histogram, with an extra feature. Here the mid point of
each class of the x-axis is marked. Then the midpoints
and the frequencies are taken as the plotting point.
These points are connected using line segments.
• We also complete the graph, that is, it's closed by
joining to the x-axis. Frequency polygon gives a less
accurate representation of the distribution, than a
histogram, as it represents the frequency of each class
by a single point not by the whole class interval.
24

25. Example
25

26. Final Product
26

27. Frequency Curve
• The frequency polygon consists of sharp turns, and ups and
downs which are not in conformity with actual conditions.
• To remove these sharp features of a polygon, it becomes
necessary to smooth it. No definite rule for smoothing the
polygon can be laid down.
• It should be understood very clearly that the curve does not,
in any way, sharply deviate from the polygon.
• In order to draw a satisfactory frequency curve, first of all, we
need to draw a frequency histogram  the frequency
polygon and ultimately the frequency curve.
27

28. Example
28

29. Cumulative Frequency (OGIVE)
• Cumulative frequency is a graph plotting
cumulative frequencies on the y-axis and class
scores on the x-axis.
• The difference between frequency curve and
an ogive is that in the later we plot the
cumulative frequency on the y-axis rather
than plotting the individual frequencies.
• Advantage : it enables median, quartiles, etc
to be studied from the graph.
29

30. Example
30

31. Example
31

32. 32

33. (B) Flow chart
• A diagram of the sequence of movements or
actions of people or things involved in a
complex system or activity.
33

34. Purpose
• The purpose of a flow chart is to provide
people with a common language or reference
point when dealing with a project or process.
• Flowcharts use simple geometric symbols and
arrows to define relationships.
34

35. Example
35

36. (C) Graphs on Logarithmic and Semi-
Logarithmic Axes
• In a semilogarithmic graph, one axis has a
logarithmic scale and the other axis has a
linear scale.
• In log-log graphs, both axes have a logarithmic
scale.
• The idea here is we use semilog or log-log
graph axes so we can more easily see details
for small values of y as well as large values
of y.
36

37. Semi-Logarithmic Graphs
• In the following set of
axes, the vertical scale
is logarithmic (equal
scale between powers
of 10) and the
horizontal scale
is linear (even spaces
between numbers).
There are no negative numbers on the y-axis, since we can only find the
logarithm of positive numbers. 37

38. Example
38

39. Example
39

40. Example
40

41. Example
41

42. linear T-P axes
Plot shows reasonable detail for values of x greater than 1, but
doesn't tell us much for smaller values of x or y. The points are
too close to the x-axis for us to see what is going on
42

43. Semi-logarithmic axes
43

44. Log-log Graphs
• Log-log graphs use a logarithmic scale for both
vertical and horizontal axes.
44

45. Example
45