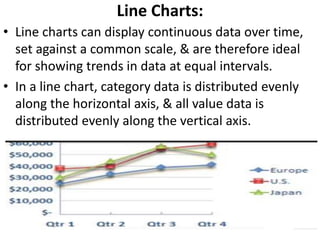
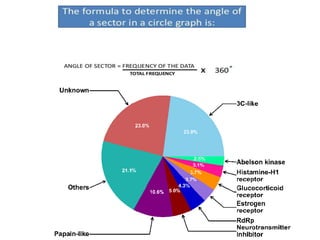
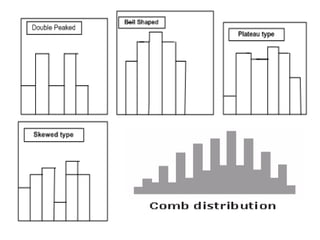
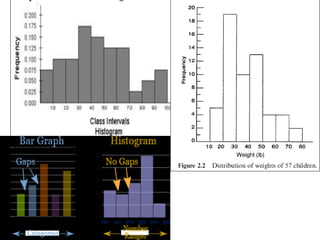
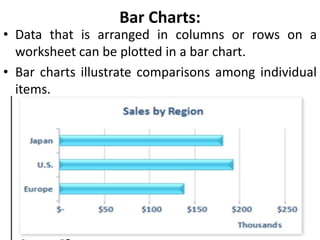
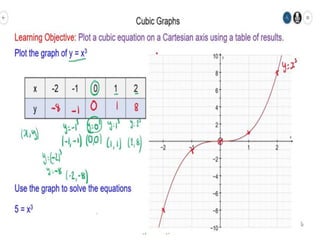
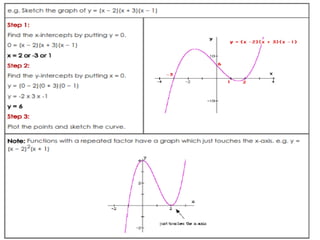
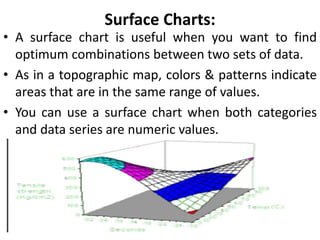
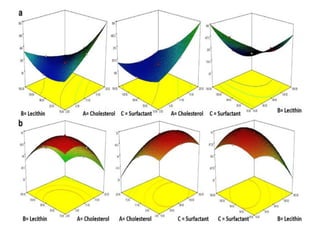
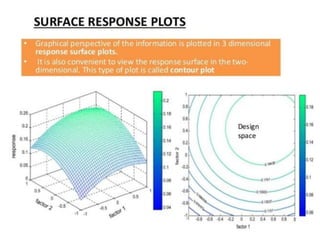
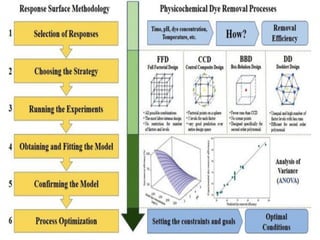
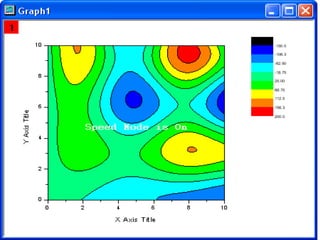
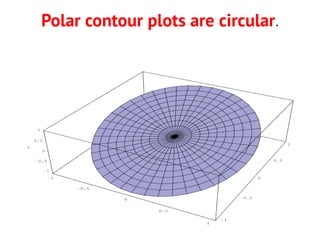
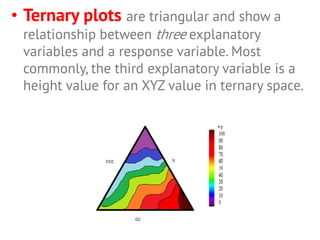
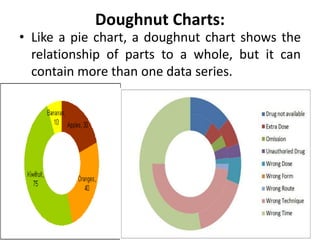
This document provides an overview of different types of graphs that can be used to present statistical data, including histograms, pie charts, bar charts, line charts, cubic graphs, response surface plots, and contour plots. It discusses the purpose and construction of each graph type, advantages and disadvantages, and provides examples of how and when each type of graph might be used. The overall goal is to help students identify, construct, and properly label different graphs to effectively communicate statistical data.

1. Unit: 3
Graphs
Ravinandan A P
Assistant Professor
Sree Siddaganga College of Pharmacy
Tumkur-02

2. Presentation Outlines
1. Introduction
2. Histogram
3. Pie Chart
4. Cubic Graph
5. Response surface plot
6. Counter Plot graph
Learning Outcomes
At the end of the
session students should
be able to:
1. Identify and
construct graphs
form the available
data.
2. Labeling of graphs.

3. • Important, convincing appealing & easily
understood method of presenting the
statistical data is the use of diagrams &
graphs.
• They are nothing but geometrical figures like
points, lines, bars, squares, rectangles, circles,
cubes, picture, maps and charts.

4. Advantages
• Graphs & Diagrams are more visual aids which
give a bird’s eye view of a given set of
numerical data
• These are more attractive, impressive than the
set of numerical data.
• They register a meaningful impression on the
mind almost before we think.
• Save a lot of time to understand the data.

5. General rule for constructing graphs and diagrams
1. Neatness
2. Title & footnotes
3. Selection of scale
4. Proportions between width & height
5. Choice of a graph and / or diagram
6. Source note & number
7. Index
8. Simplicity

6. • Data collected & compiled from
experimental work, registers, records, or
surveys should be accurate & complete.
• They must be checked for accuracy &
adequacy before processing further.
• The data that are obtained on the units of
the population or sample under inquiry
are in terms of the observations taken on
the variable or attribute associated with
the units of the population or sample.

7. Types of diagrams
1. One dimensional diagrams, ex: line & bar
diagrams
2. Two - dimensional diagrams, ex: rectangles,
squares, circles, pie diagrams
3. Three - dimensional diagrams, ex: cubes,
spheres, prisms, cylinders and blocks
4. Pictograms
5. Cartograms

8. Column Charts:
• These are useful for showing data changes
over a period of time or for illustrating
comparisons among items.
• In column charts, categories are typically
organized along the horizontal axis & values
along the vertical axis.

9. Line Charts:
• Line charts can display continuous data over time,
set against a common scale, & are therefore ideal
for showing trends in data at equal intervals.
• In a line chart, category data is distributed evenly
along the horizontal axis, & all value data is
distributed evenly along the vertical axis.

11. Pie Charts:
• Data that is arranged in one column or row only on
a worksheet can be plotted in a pie chart.
• Pie charts show the size of items in one data series,
proportional to the sum of the items.
• The data points in a pie chart are displayed as a
percentage of the whole pie.

12. • A pie chart is a type of graph that
represents the data in the circular graph.
• The slices of pie show the relative size of
the data.
• It is a type of pictorial representation of
data.
• A pie chart requires a list of categorical
variables and the numerical variables.
• Here, the term “pie” represents the whole,
and the “slices” represent the parts of the
whole.

13. • The “pie chart” is also known as “circle
chart”, that divides the circular statistical
graphic into sectors or slices in order to
illustrate the numerical problems.
• Each sector denotes a proportionate part of
the whole.
• To find out the composition of something,
Pie-chart works the best at that time.
• In most cases, pie charts replace some other
graphs like the bar graph, line plots,
histograms, etc.

14. Advantages
• The picture is simple and easy-to-understand
• Data can be represented visually as a fractional
part of a whole
• It helps in providing an effective communication
tool for the even uninformed audience
• Provides a data comparison for the audience at
a glance to give an immediate analysis or to
quickly understand information
• No need for readers to examine or measure
underlying numbers themselves, which can be
removed by using this chart
• To emphasize a few points you want to make,
you can manipulate pieces of data in the pie
chart

15. Disadvantages
• It becomes less effective, if there are too
many pieces of data to use
• If there are too many pieces of data. Even if
you add data labels and numbers may not
help here, they themselves may become
crowded and hard to read
• As this chart only represents one data set,
you need a series to compare multiple sets
• This may make it more difficult for readers
when it comes to analyze and assimilate
information quickly

17. Histogram:
• A histogram is similar to a bar chart, but the base of the
rectangle has a length exactly equal to the class width of
the corresponding interval.
• a graphical display of data using bars of different
heights. It is similar to a Bar Chart, but
a histogram groups numbers into ranges . The
height of each bar shows how many fall into each
range.
• As the rectangle is centered on the average of the lower
and upper class limits, the rectangles of a class interval are
adjacent to the rectangles of adjoining class intervals--
there are no spaces between rectangles.

18. Use of Histogram
• The histogram is a popular graphing tool.
• It is used to summarize discrete or
continuous data that are measured on an
interval scale.
• It is often used to illustrate the major
features of the distribution of the data in a
convenient form.

19. • Histograms are of five types. They are:
• Bell shaped: It can be applied for concepts such as
average and standard deviation.
• Double peaked: It is used to compare two different
processes with different centers.
• Plateau distribution: It is used when the process is not
well-defined.
• Since the process is handled by different people in
different ways, different measurements arise with none
standing out. Plateau distribution is used to define an
efficient process.
• Comb type distribution: It is a result of the faulty
construction of the histogram, with data combined
together into a group called „greater than?.
• Skewed distribution: The skewed distribution is
asymmetrical since a natural limit prevents outcomes on
one side. A distribution of analyses of a very pure
product would be skewed, as any product cannot be
more than 100 percent pure.

22. Bar Charts:
• Data that is arranged in columns or rows on a
worksheet can be plotted in a bar chart.
• Bar charts illustrate comparisons among individual
items.

23. Step 1: Find the x-intercepts by putting y = 0.
Step 2: Find the y-intercept by putting x = 0.
Step 3:
Plot the points above to sketch the
cubic curve.
CUBIC GRAPHS
A cubic function is a polynomial of degree three.
e.g. y = x3 + 3x2 − 2x + 5
Cubic graphs can be drawn by finding the x and y
intercepts.
Because cubic graphs do not have axes of symmetry
the turning points have to be found using calculus.
Sketching Cubics
Method 1: Factorisation.
If the equation is in the form y = (x − a)(x − b)(x − c)
the following method should be used:

26. Surface Charts:
• A surface chart is useful when you want to find
optimum combinations between two sets of data.
• As in a topographic map, colors & patterns indicate
areas that are in the same range of values.
• You can use a surface chart when both categories
and data series are numeric values.

27. Response surface plot
• Response surface plots such
as contour and surface plots are useful for
establishing desirable response values and
operating conditions.
• In a contour plot, the response surface is viewed
as a two-dimensional plane where all points that
have the same response are connected to
produce contour lines of constant responses.
• Use a surface plot to see how
fitted response values relate to two continuous
variables based on a model equation. A surface
plot is a three-dimensional wireframe graph that is
useful for establishing desirable response values
and operating conditions.

28. • The response surface method (RSM) is a
representative method for generating meta-
models.
• The original model is evaluated at multiple
sample points and the meta-model is
constructed usually as a linear or a quadratic
function.
• The coefficients of the meta-model function
are determined by minimizing the error

32. Counter Plot graph
• A contour plot is a graphical technique for
representing a 3-dimensional surface
by plotting constant z slices,
called contours, on a 2-dimensional format.
This contour plot shows that the surface is
symmetric and peaks in the center.
• Definition. The contour plot is formed by:
Vertical axis: Independent variable 2.

33. Counter Plot graph
• Contour plots (sometimes called
Level Plots) are a way to show a three-
dimensional surface on a two-dimensional
plane.
• These contours are sometimes called z-
slices or iso-response values.
• This type of graph is widely used in
cartography, where contour lines on a
topological map indicate elevations that are
the same

34. • Use a contour plot to see how a response variable
relates to two predictor variables.
A contour plot contains the following elements:
1.Predictors on the x- and y-axes.
2.Contour lines that connect points that have
the same response value.
3.Colored contour bands that represent ranges
of the response values.
• Three Types:
1. Rectangular contour plot
2. Polar contour plots are circular.
3. Ternary plots

36. Types
• The most common form is the rectangular
contour plot, which is (as the name
suggests) shaped like a rectangle.

37. Polar contour plots are circular.

38. • Ternary plots are triangular and show a
relationship between three explanatory
variables and a response variable. Most
commonly, the third explanatory variable is a
height value for an XYZ value in ternary space.

39. Doughnut Charts:
• Like a pie chart, a doughnut chart shows the
relationship of parts to a whole, but it can
contain more than one data series.

40. Bubble Charts:
• X values are listed in the first column & corresponding y
values & bubble size values are listed in adjacent columns,
can be plotted in a bubble chart.
• For ex, you would organize your data as shown in the
following example.

41. Thank
You