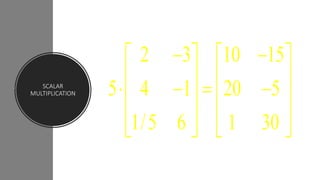
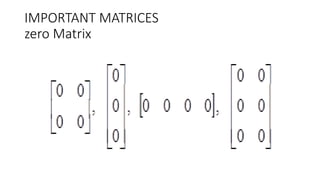
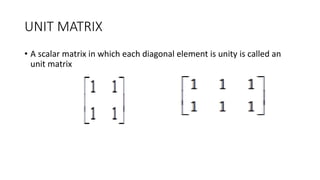
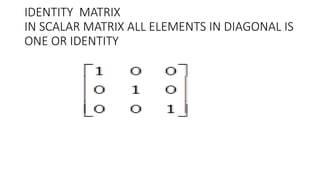
This document discusses different types of matrices including diagonal, scalar, identity, triangular, and complex matrices. It provides definitions and examples of each. Operations on matrices such as addition, subtraction, and multiplication are covered. Matrix multiplication is demonstrated using examples. Properties of matrix operations like addition and subtraction being commutative vs anti-commutative are explained.

1. CHAPTER 01
MATRIX THEORY
TYPES OF MATRICES
By Sanaullah
Memon

2. INTRODUCTION

3. IMPORTANT MATRICES
zero Matrix

4. DIAGONAL MATRICES
• A square matrix who’s each element is zero with at least one non-zero
diagonal element is called diagonal matrix.
• aij is non-zero when i = j.

5. SCALAR MATRIX
• A diagonal matrix in which all elements are equal is called a scalar
matrix

6. UNIT MATRIX
• A scalar matrix in which each diagonal element is unity is called an
unit matrix

7. IDENTITY MATRIX
IN SCALAR MATRIX ALL ELEMENTS IN DIAGONAL IS
ONE OR IDENTITY

8. UPPER AND LOWER TRAINGULAR MATRICES
A square matrix in which each element below the principal diagonal is zero is, said to be upper triangular matrix
and a square matrix in which every element above the principal diagonal is zero is, called lower triangular matrix.

9. COMPLEX MATRIX
• Definition: A matrix is said to be a triangular matrix if it is either upper
triangular or lower triangular matrix.
• A matrix whose at least one element is complex number or purely
imaginary number is called complex matrix

10. TRACE OF MATRIX
trace(A) = 6 + 5 - 9 = 2.

11. EQUALITY OF MATRICES
• Two matrices A and B are said to be equal if and only if they have the
same order and each element of one is equal to the corresponding
element of the other
Then A = B because the order of matrices A and B is same and aij = bij for all i and j.

12. OPERATION ON
MATRICES

13. CONTENTS
OPERATIONS ON MATRICES
Scalar Multiplication, Addition &
Subtraction of Matrices
Multiplication of Matrices

14. MULTIPLICATION OF MATRICES
𝐴3,3 =
3 5 5
2 1 1
2 2 4
𝐵3,3=
1 2 3
1 1 3
1 3 2
NUMBER COLUMNS OF A= NUMBER OF ROWS B

15. MULTIPLICATION
• 𝐴𝐵3,3 =
3 ∗ 1 + 5 ∗ 1 + 5 ∗ 1 3 ∗ 2 + 5 ∗ 1 + 5 ∗ 3 3 ∗ 3 + 5 ∗ 3 + 5 ∗ 2
4 8 11
8 13 20
𝐴𝐵3,3=
13 26 31
4 8 11
8 13 20

16. MULTIPLICATION
AB









 

035
742
101










 32
40
16



























1730
392
28
304315200365
374412270462
314011210061
Here A is 3 × 3 matrix and B is a 3 × 2 matrix and the resultant
matrix AB is 3 × 2 matrix.
REMARK: Can you compute B.A? The answer is simply no. Why? Because the number of columns of B
is 2 and number of rows of A is 3. Hence, B.A is not confirmable for multiplication.

17. PROPERTIES OF MATRICES
 i. Two matrices are, said to be confirmable for addition or subtraction if and only if their order is same. ii. If
the matrices A, B and C are confirmable for addition/subtraction, then
 a. A + A = 2 A b. A – A = O c. A + A + … + A = n A
 d. A + B = B + A e. A – B ≠ B – A f. A + (B + C) = (A + B) + C
 From (d) and (e) we observe that matrix addition is commutative but same is not true for matrix subtraction.
In fact, matrix subtraction is anti-commutative. Property (f) is known as “Associative law of addition.
 iii. A set of all matrices “M” confirmable under addition form an “Abelian Group”. For if A, B, C M, then
 A + B M [Closure property under addition]
 A + (B + C) = (A + B) + C [Existence of associate law under addition]
 A + O = O + A = A [Existence of identity matrix under addition]
 A + (-A) = (-A) + A = O, where O M [Existence of inverse matrix under addition]
 A + B = B + A [Existence of commutative law for addition]

18. ADDITION& SUBTRACTION OF MATRICES
• 𝐴3,3 =
2 1 2
2 1 1
4 2 2
𝐵3,3=
2 2 2
1 4 1
1 3 3
• 𝐴 + 𝐵 =
4 3 4
3 5 2
5 5 5
SOLVE YOURE SELF A-B
• ORDER MUST BE EQUAL TWO MATRIX THEN ADDITION POSSIBLE

19. EXAMPLE
).A(ffind,2x22x)x(fand
31
21
AIf  





Solution: In matrix algebra, f(A) = A2 + 2A – 2I. Now



















114
83
31
21
31
212A . Thus
f(A) = A2 + 2A – 2I = 
























156
123
20
02
62
42
114
83

20. MULPLICATION
INVERSE

21. SCALAR
MULTIPLICATION
2 3 10 15
5 4 1 20 5
1/5 6 1 30
    
         
      

22. The end