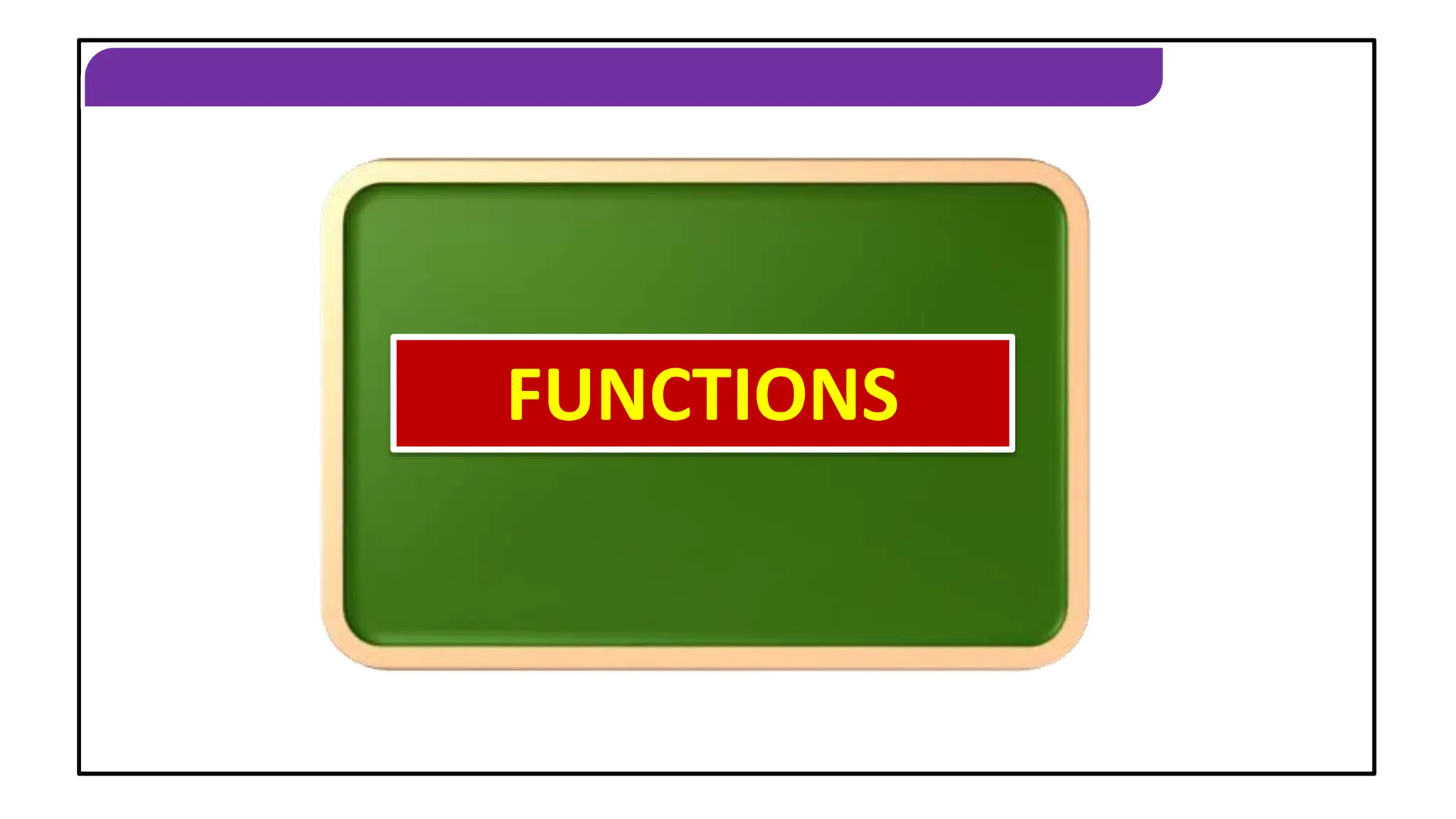
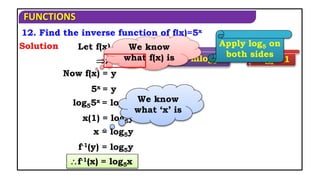
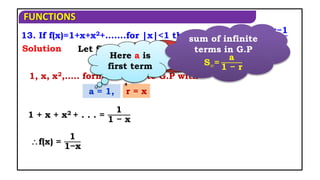
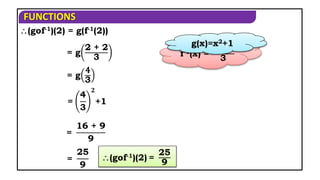
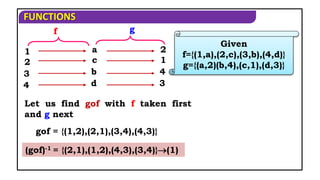
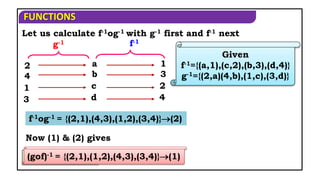
The document discusses various exercises involving functions, including operations like addition, subtraction, multiplication, and composition. It provides examples of functions defined over specific sets, explores characteristics of functions (like whether they are odd or even), and discusses inverse functions. Additionally, it includes proofs and step-by-step solutions to determine properties, transformations, and inversions of given functions.




































![FUNCTIONS
(1)
If 0 x 2
If 2 < x 3
Solution
then show that f[0, 3] [0, 3] and find fof ?
19. If f : [0, 3] [0, 3] is defined by
1 + x, 0 x 2,
3 - x, 2 < x 3
f(x) =
1 1 + x 3
-3 - x < -2
(2)
3 - 3 3 - x < 3 - 2
0 3 - x < 1
If you add 1
If you
multiply with
‘-’
If you add ‘3’
from (1) and (2) if you
substitute any
value [0,3] in f(x)
the resultant
must lie in [0,3]](https://image.slidesharecdn.com/mat1ajrfunm04ex1prob-240423114859-d568424c/85/FUNCTION-EX-1-PROBLEMS-WITH-SOLUTION-UPTO-JEE-LEVEL-46-320.jpg)
![FUNCTIONS
From (1) and (2) f [0,3] [0,3]
When 0 x 1 we have
fof(x) = f(f(x))
= f(1+x)
= 2+x [∵11+x2]
= 1+1+x
When 1<x2 we have
fof(x) = f(f(x))
= f(1+x)
= 3-(1+x)
Here
f(x)=1+x
Here
f(x)=3-x
=2-x [∵2<1+x3]](https://image.slidesharecdn.com/mat1ajrfunm04ex1prob-240423114859-d568424c/85/FUNCTION-EX-1-PROBLEMS-WITH-SOLUTION-UPTO-JEE-LEVEL-47-320.jpg)
![FUNCTIONS
When 2<x3 we have
fof(x)=f(f(x))
=f(3-x)
=1+3-x
=4-x [∵ 03-x<1]
fof(x)=
2+x,0x<1
2-x,1<x2
4-x,2<x3](https://image.slidesharecdn.com/mat1ajrfunm04ex1prob-240423114859-d568424c/85/FUNCTION-EX-1-PROBLEMS-WITH-SOLUTION-UPTO-JEE-LEVEL-48-320.jpg)
