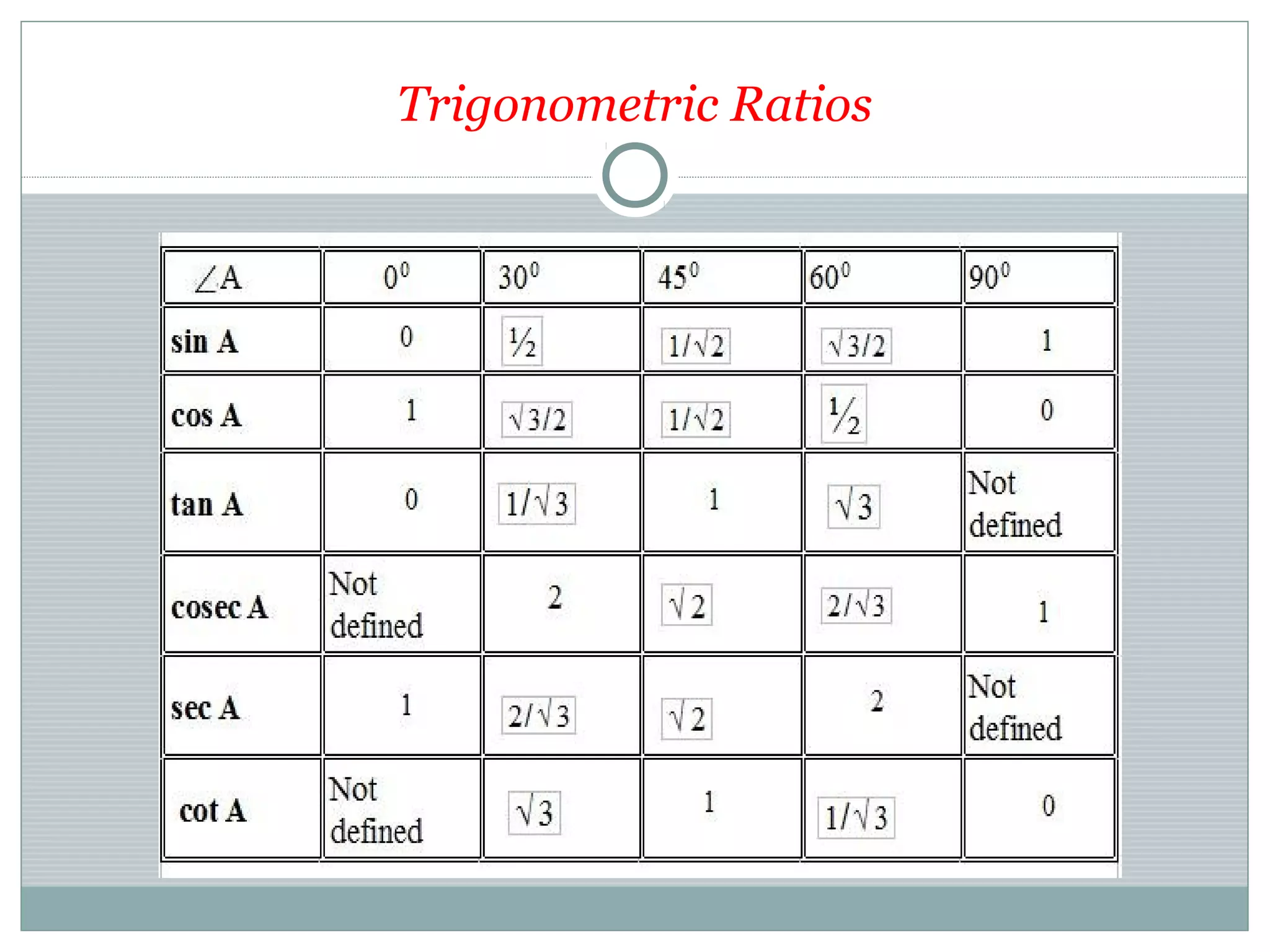
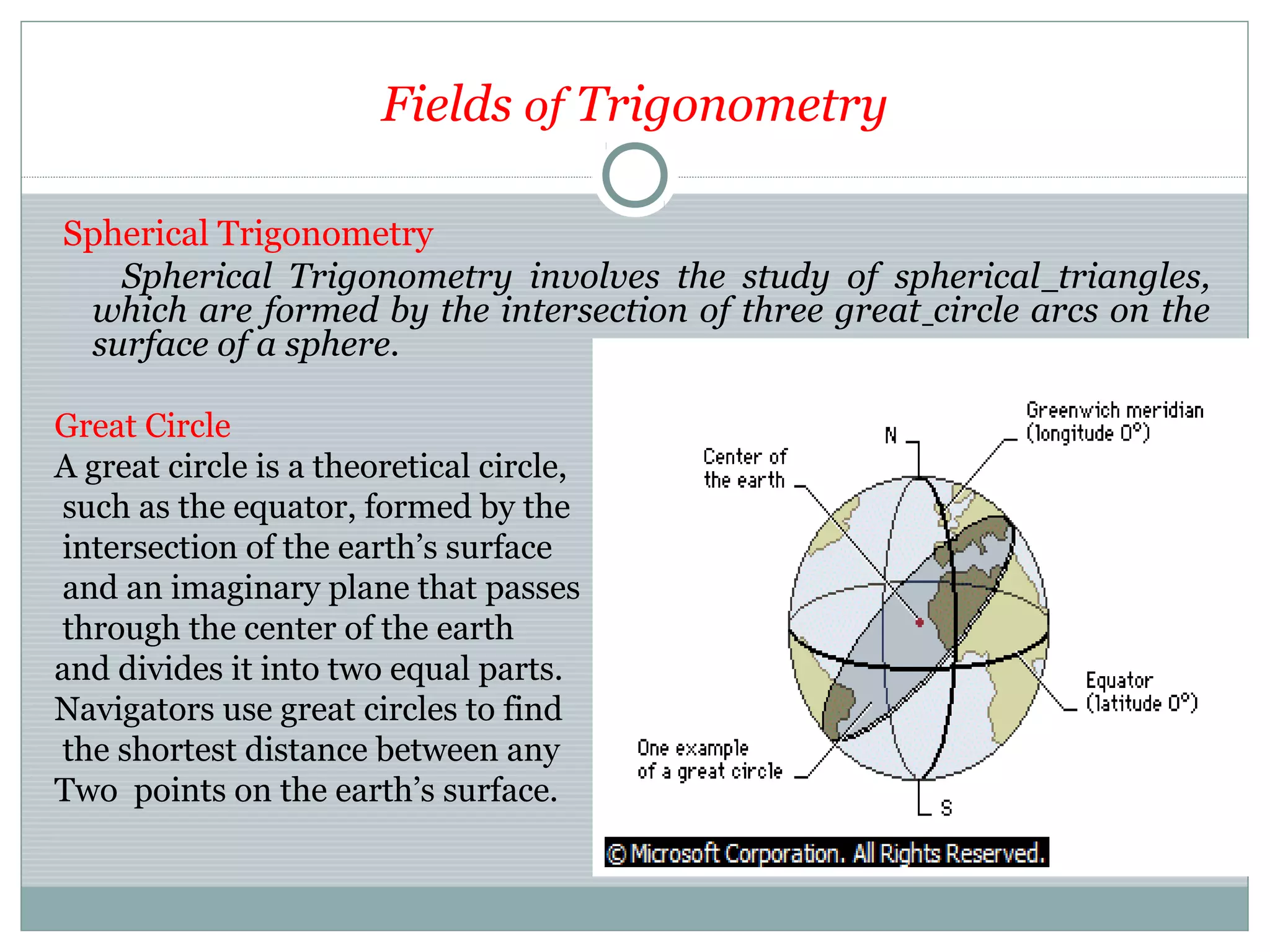
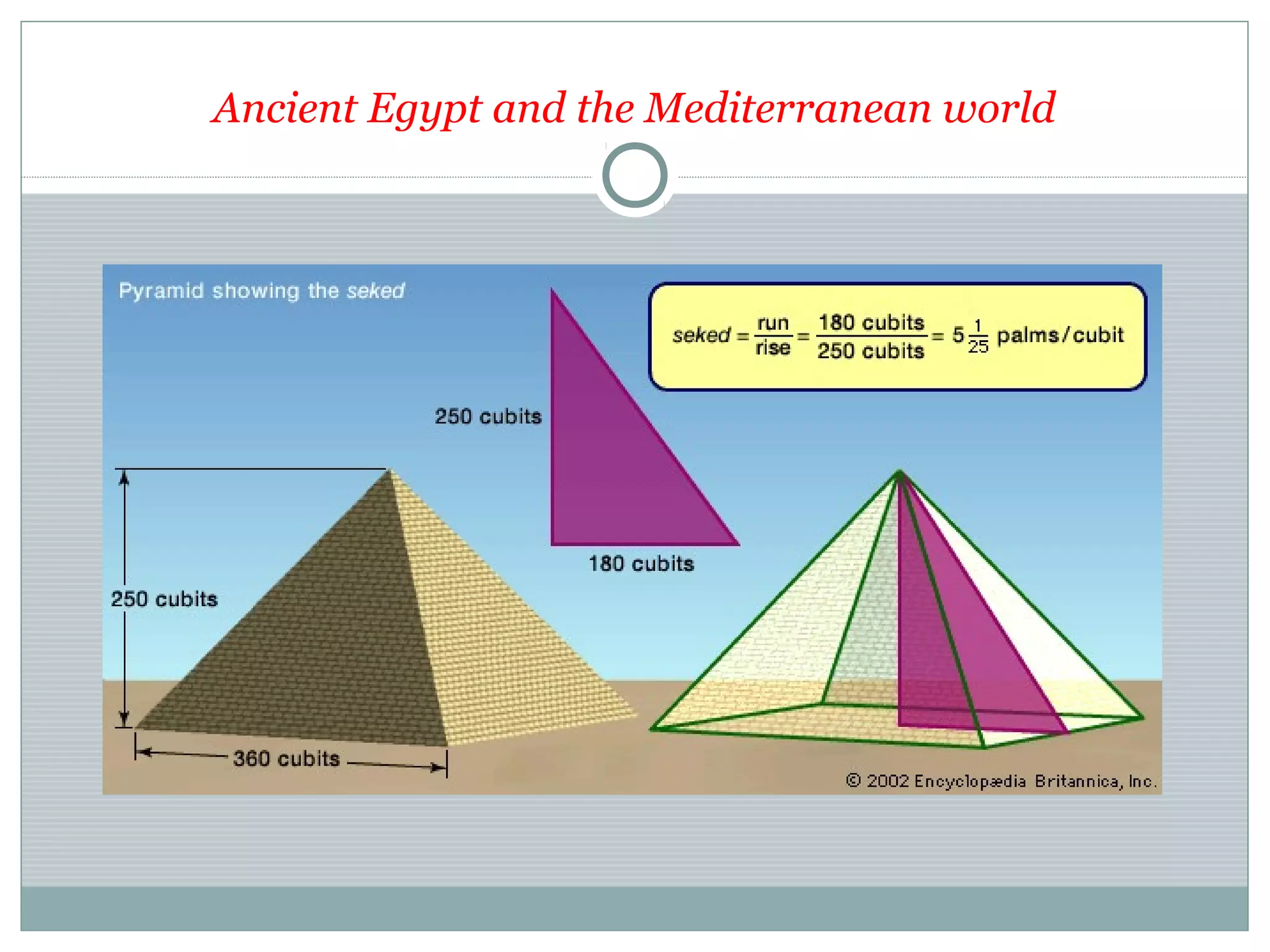
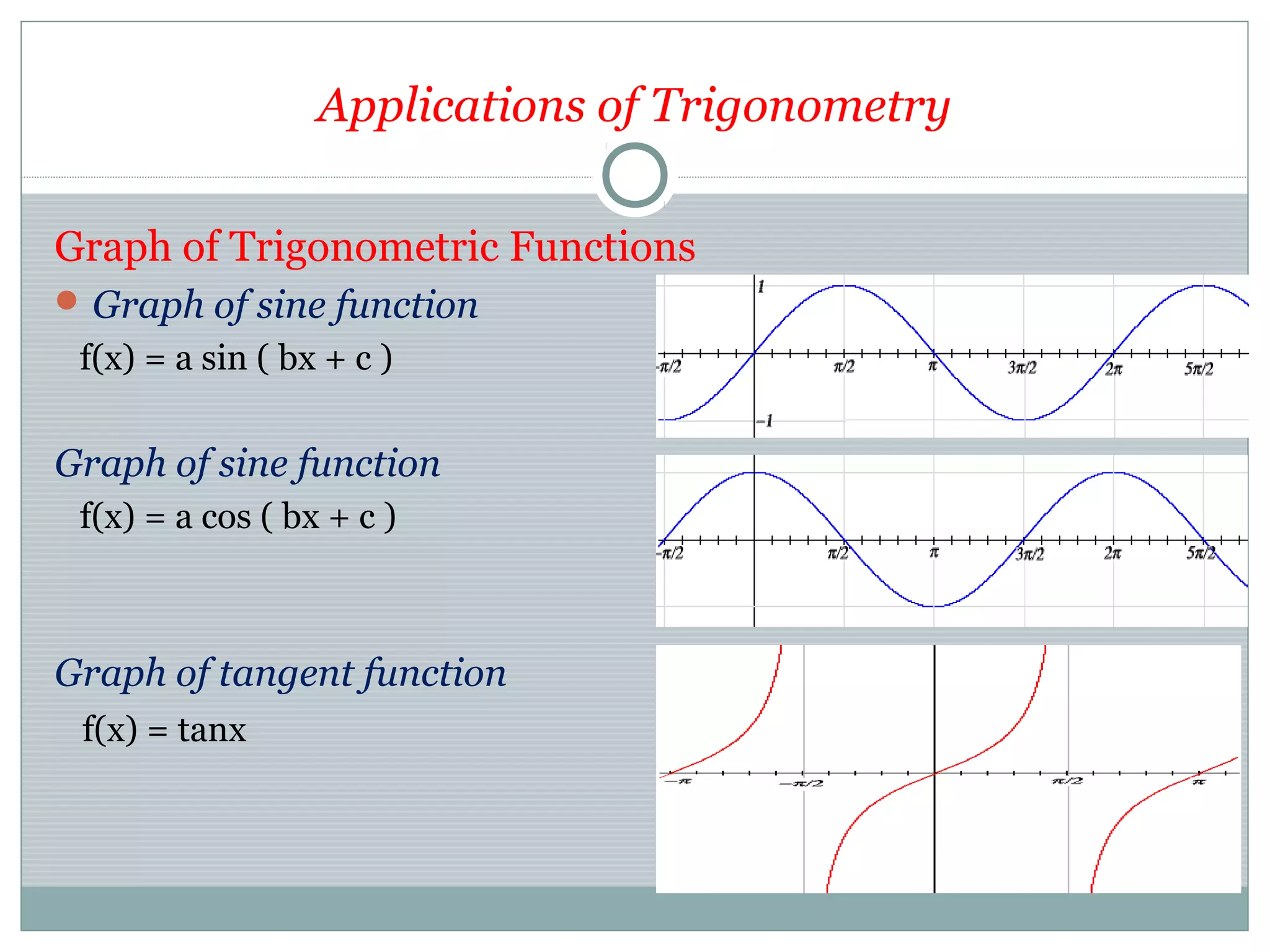
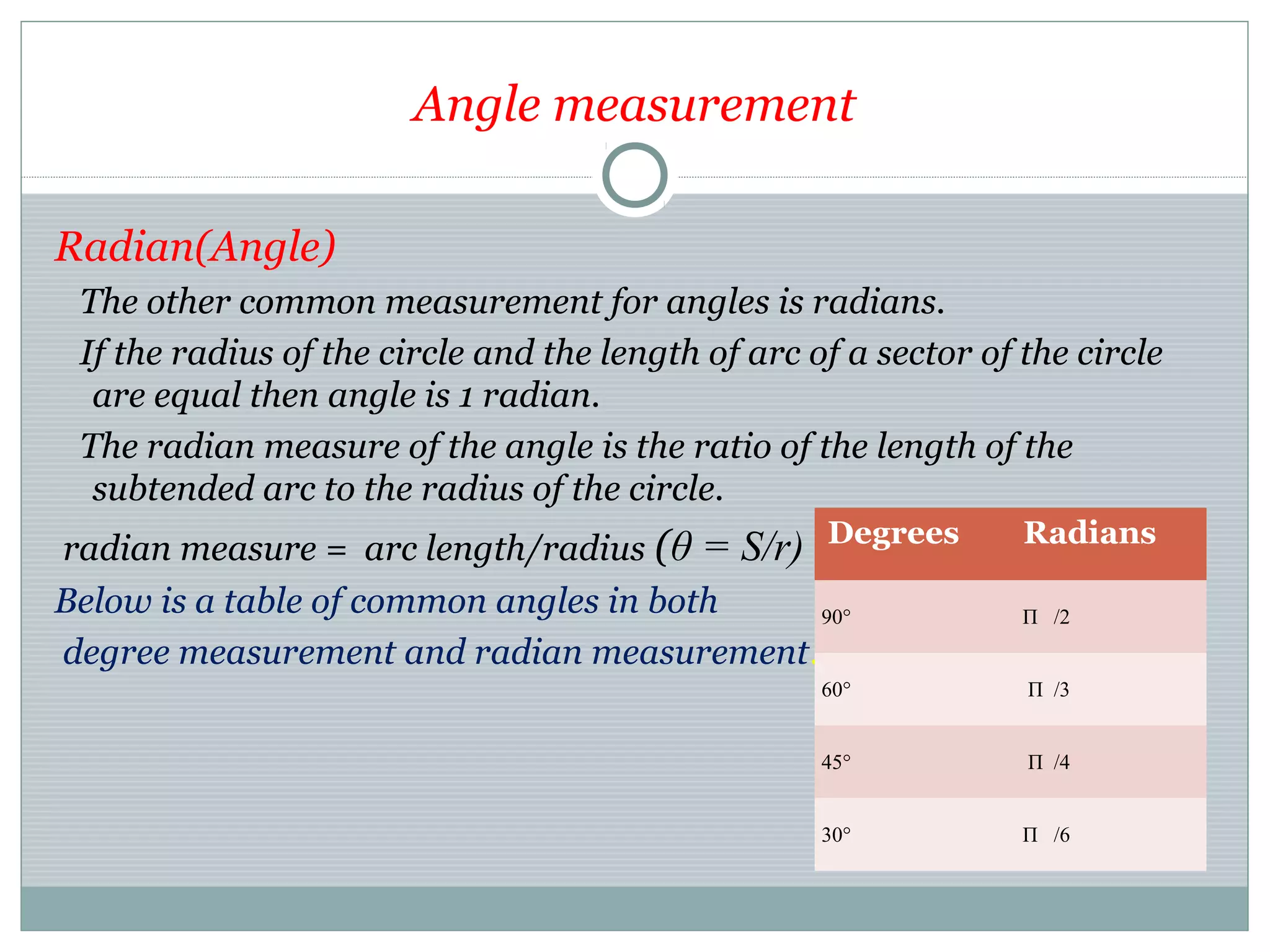
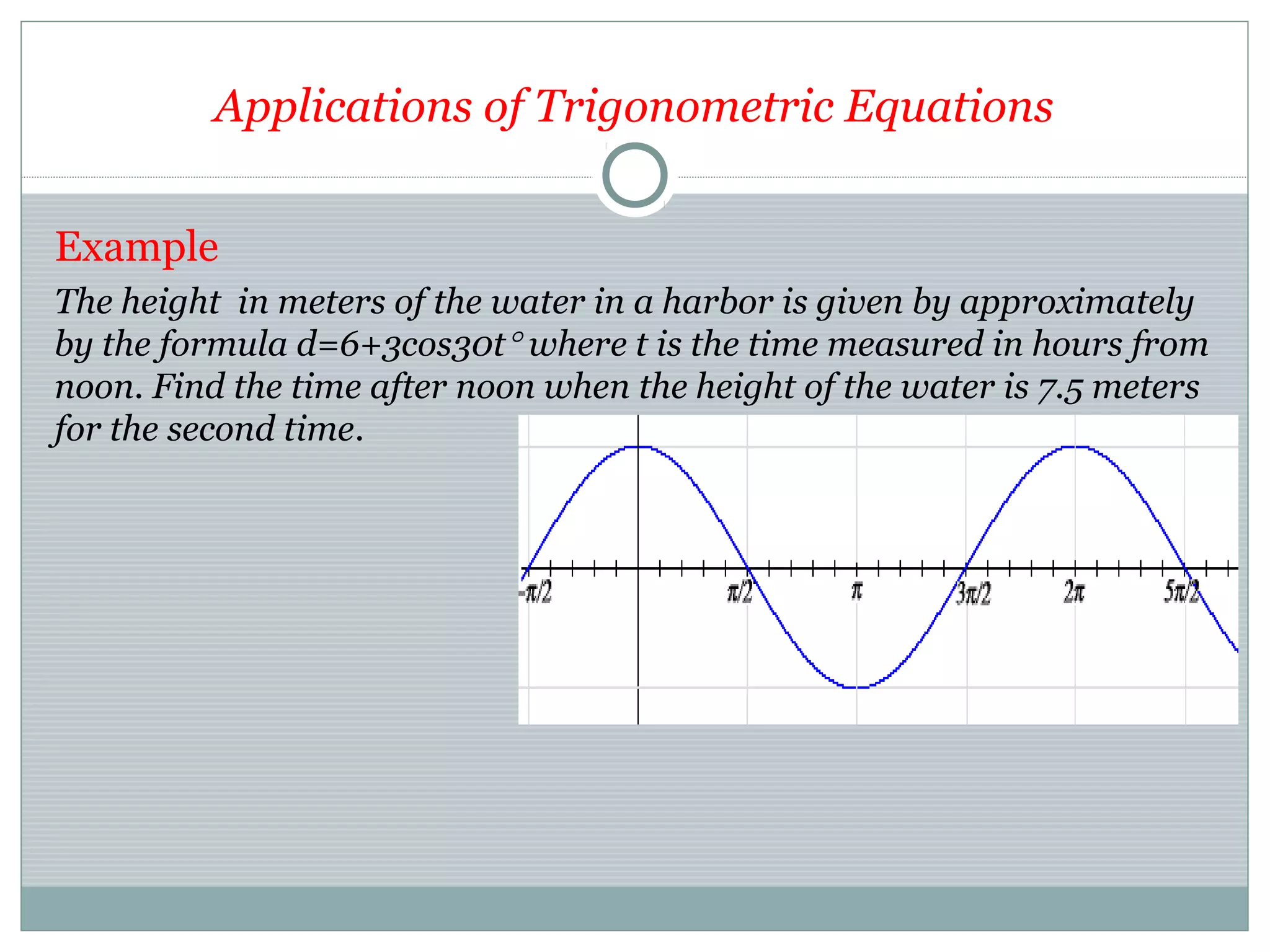
This document provides an overview of trigonometry and its applications. It begins with definitions of trigonometry, its history and etymology. It discusses trigonometric functions like sine, cosine and their properties. It covers trigonometric identities and applications in fields like astronomy, navigation, acoustics and more. It also discusses angle measurement in degrees and radians. Laws of sines and cosines are explained. The document concludes with examples of trigonometric equations and their applications.

1. DA PUBLIC SCHOOL (O&A LEVELS)

2. BY : MUSHTAQ-UR-REHMAN
HEAD OF MATHEMATICS DEPARTMENT
D.A.P.S. O & A LEVELS
Trigonometry and Applications

3. “Indeed we have created everything
in a proper measure.”
(Surah Al-Qamr)
Allah says in the Holy Quran

4. Trigonometry and Applications
Fields of discussion
 What is Mathematics?
 Prince of Mathematicians
 What is Trigonometry?
 History and the meaning of the word sine and cosine.
 Trigonometric functions, Circular functions or cyclometric functions
 Fields of Trigonometry
 Ancient Egypt and the Mediterranean world
 Applications of Trigonometry
 Angle measurement
 Properties of sines and cosines
 The Law(Rule) of sines,cosines
 Trigonometric Equations
 Applications of Trigonometric Equations

5. What is Mathematics?
Etymology
The word “Mathematics" comes from the Greek word (máthēma), which
means learning, study, science, and additionally more technical
meaning “Mathematical study",
Mathematics (Definition)
A group of related subjects , including ALGEBRA, GEOMETRY,
TRIGONOMETRY and CALCULUS, concerned with the study of number
,quantity, structure, shape and space.
Applications
Mathematics is used throughout the world as an essential tool in many
fields, including natural science, engineering, medicine, and the social
sciences.

6. Prince of Mathematicians
Carl Friedrich Gauss
Himself known as the
"prince of mathematicians“,
referred to Mathematics as
"the Queen of the Sciences".
This German Mathematician contributed
to many areas of Mathematics, including
probability theory, algebra, and geometry.
He proved that every polynomial has at
least one root, or solution; this theory is
known as the fundamental theory
of algebra. Gauss also applied his
mathematical work to theories of
electricity and magnetism.

7. What is Trigonometry?
Etymology
The word Trigonometry is derived from three Greek words ‘tries’(three),
‘goni’(angle) and ‘metron’(measurement). So literally, this word means
“measurement of the triangle”.
Trigonometry (Definition)
The branch of Mathematics concerned with the properties of
trigonometric functions and their application to the determination of the
sides and angles of triangles.
Trigonometry has now a wide application in higher Mathematics
in fact, any attempt to study Higher Mathematics would be an utter
failure without a working knowledge of trigonometry.
It has applications in both pure mathematics and applied mathematics,
where it is essential in many branches of science and technology.

8. History and the meaning of the word sine and cosine
Interesting word history for "sine”
The Hindu mathematician Aryabhata (about 475–550 A.D.) used the
Sanskrit word “jya” or “jiva” for the half-chord which was sometimes
shortened to jiva. This was brought into Arabic as jiba, and written in Arabic
simply with two consonants jb, vowels not being written. Later, Latin
translators selected the word sinus to translate jb thinking that the word was
an arabic word jaib, which meant bosom, fold, or bay, The Latin word for
bosom, bay, or curve is “sinus”. In English, sinus was imported as "sine".
This word history for "sine" is interesting because it follows the path of
trigonometry from India, through the Arabic language from Baghdad
through Spain, into western Europe in the Latin language, and then to
modern languages such as English.

9. Trigonometric functions, Circular functions or
cyclometric functions
Any of a group of functions expressible in terms of the ratios of
the sides of right-angled triangle.
 Sine Ratio The sine of an angle in a right triangle equals the opposite
side divided by the hypotenuse:
sin =opp/hyp
 Cosine Ratio. Cosines are just sines of the complementary angle. Thus,
the name "cosine" ("co" being the first two letters of "complement").
The complementary angle equals the given angle subtracted from a right
angle, 90°. For instance, if the angle is 30°, then its complement is 60°.
Generally, for any angle x,
cos =adj/hyp
cos x = sin (90° – x). Or cos 50 = sin (90 – 50) = sin40ᵒ ᵒ
 Tangent Ratio tanx = sinx/cosx
tanx = opp/adj

10. Trigonometric functions, Circular functions or
cyclometric functions
 Secant:
sec q = 1/cos q
 Cosecant:
csc q = 1/sin q
 Cotangent:
cot q = 1/ tan q
cot q = cos q/sin q
tan q = sin q/cos q

11. Trigonometric Ratios

12. Trigonometric Identities
 The following formulas, called identities, which show the relationships
between the trigonometric functions, hold for all values of the angle θ, or of
two angles, θ and φ, for which the functions involved are

14. Fields of Trigonometry
Plane Trigonometry
In many applications of trigonometry the
essential problem is the solution of triangles.
If enough sides and angles are known, the
remaining sides and angles as well as
the area can be calculated, and the triangle
is then said to be solved. Triangles can be
solved by the law of sines and the law of
cosines.
Surveyors apply the principles of geometry
and trigonometry in determining the shapes,
measurements and position of features on
or beneath the surface of the Earth. Such
topographic surveys are useful in the design
of roads, tunnels, dams, and other structures.

15. Fields of Trigonometry
Spherical Trigonometry
Spherical Trigonometry involves the study of spherical triangles,
which are formed by the intersection of three great circle arcs on the
surface of a sphere.
Great Circle
A great circle is a theoretical circle,
such as the equator, formed by the
intersection of the earth’s surface
and an imaginary plane that passes
through the center of the earth
and divides it into two equal parts.
Navigators use great circles to find
the shortest distance between any
Two points on the earth’s surface.

16. Fields of Trigonometry
Analytic Trigonometry
Analytic Trigonometry combines the use of a coordinate system,
such as the Cartesian coordinate system used in analytic
geometry, with algebraic manipulation of the various
trigonometry functions to obtain formulas useful for scientific
and engineering applications.

18. Ancient Egypt and the Mediterranean world
Several ancient civilizations—in particular, the Egyptian,
Babylonian, Hindu, and Chinese—possessed a considerable
knowledge of practical geometry, including some concepts of
trigonometry.
A close analysis of the text, with its accompanying figures,
reveals that this word means the slope of an incline, essential
knowledge for huge construction projects such as the pyramids.
It shows that the Egyptians had at least some knowledge of the
numerical relations in a triangle, a kind of “proto-
trigonometry.”

19. Ancient Egypt and the Mediterranean world

20. Applications of Trigonometry
.
 Fields that use trigonometry or trigonometric functions include Astronomy
(especially for locating apparent positions of celestial objects(star or planet),
in which spherical trigonometry is essential) and hence navigation (on the
oceans, in aircraft, and in space), to measure distances between landmarks,
and in satellite navigation systems. The sine and cosine functions are
fundamental to the theory of periodic functions such as those that describe
sound and light waves.
 Music theory, acoustics(study of sound ), optics, electronics, probability
theory, statistics, biology, medical imaging (CAT scans and ultrasound),
pharmacy, chemistry, number theory cryptology(coding), seismology,
meteorology, oceanography, many physical sciences, land surveying and
geodesy(cartography), architecture, phonetics (sounds of human speech),
economics, electrical engineering, mechanical engineering, civil engineering,
computer graphics, crystallography and game development.

21. Applications of Trigonometry
Marine sextants like this are used to measure the angle of the sun or
stars with respect to the horizon. Using trigonometry and a marine
chronometer(timer), the position of the ship can then be determined from
several such measurements.

22. Applications of Trigonometry
Wave Mathematics
Waves are familiar to us from the ocean, the study of sound, earthquakes, and
other natural phenomenon. Ocean waves come in very different sizes to fully
understand waves, we need to understand measurements associated with
these waves, such as how often they repeat (their frequency), and how long
they are (their wavelength), and their vertical size (amplitude).
The importance of the sine and
cosine functions is in describing
periodic phenomena—the
vibrations of a violin string,
the oscillations of a clock pendulum,
or the propagation of electromagnetic
waves, sound and light waves.

23. Applications of Trigonometry
Sine waves in nature
i)Sound waves are sine waves whenever we listen to music ,
we are actually listening to sound waves.
ii) light waves are also sine waves.
iii)Radio waves are sine waves.
iv)Simple harmonic motion of a spring when pulled
and released is a sine wave.
v) Alternating current (AC) is a sine wave.
vi) Pendulum clock oscillations are sinusoidal in
nature
vii) Waves of ocean are sinusoidal .
viii) The vibrations of guitar strings when played are
sinusoidal in nature.

24. Applications of Trigonometry
Graph of Trigonometric Functions
Graph of sine function
f(x) = a sin ( bx + c )
Graph of sine function
f(x) = a cos ( bx + c )
Graph of tangent function
f(x) = tanx

25. Applications of Trigonometry
The 17th and 18th centuries saw the invention of numerous
mechanical devices. A notable application was the science of artillery
—and in the 18th century it was a science. Galileo Galilei (1564–1642)
discovered that any motion—such as that of a projectile under the
force of gravity—can be resolved into two components, one horizontal
and the other vertical,
This discovery led scientists to the formula for the range of a
cannonball when its muzzle velocity v0 (the speed at which it leaves the
cannon) and the angle of elevation A of the cannon.

26. Applications of Trigonometry

27. Applications of Trigonometry
Fourier series
An infinite trigonometric series of terms consisting of constants
multiplied by sines or cosines, used in the approximation of periodic
functions.
The trigonometric or Fourier series have found numerous applications
in almost every branch of science, from optics and acoustics to radio
transmission and earthquake analysis. Their extension to non
periodic functions played a key role in the development of quantum
mechanics in the early years of the 20th century. Trigonometry, by
and large, matured with Fourier's theorem.

28. Angle measurement
The concept of angle is one of the most important concepts in geometry
and the subject of trigonometry is based on the measurement of
angles.
Degree (Angle)
There are two commonly used units of measurement for angles. The
more familiar unit of measurement is that of degrees. A circle is
divided into 360 equal degrees,
Degrees may be further divided into minutes and seconds.
For instance seven and a half degrees is now usually written 7.5°.
Each degree is divided into 60 equal parts called minutes. So seven
and a half degrees can be called 7 degrees and 30 minutes, written 7°
30'. Each minute is further divided into 60 equal parts called seconds,
and, for instance, 2 degrees 5 minutes 30 seconds is written 2° 5' 30".

29. Angle measurement
Radian(Angle)
The other common measurement for angles is radians.
If the radius of the circle and the length of arc of a sector of the circle
are equal then angle is 1 radian.
The radian measure of the angle is the ratio of the length of the
subtended arc to the radius of the circle.
radian measure = arc length/radius (θ = S/r)
Below is a table of common angles in both
degree measurement and radian measurement.
Degrees Radians
90° Π /2
60° Π /3
45° Π /4
30° Π /6

30. Angle measurement

31. Angle measurement
1. Express the following angles in radians.
(a). 12 degrees, 28 minutes, that is, 12° 28'. (b). 36° 12'.
2. Reduce the following numbers of radians to degrees, minutes, and
seconds.
(a). 0.47623. (b). 0.25412.
3. Given the angle a and the radius r, to find the length of the
subtending arc. a = 0° 17' 48", r = 6.2935.
4. Find the length to the nearest inch of a circular arc of 11 degrees
48.3 minutes if the radius is 3200 feet.
5. Given the length of the arc l and the angle a which it subtends at
the center, to find the radius.
a = 0° 44' 30", l = .032592

32. Properties of sines and cosines
1.Sine and cosine are periodic functions of period 360° or 2Π .,
sin (t + 360°) = sin t, and sin (t + 2π ) = sin t,
cos (t + 360°) = cos t. cos (t + 2π ) = cos t.
2 . Sine and cosine are complementary:
cos t = sin (π /2 – t) , sin t = cos (π /2 – t)
3 .The Pythagorean identity sin2
t + cos2
t = 1.
4. Sine is an odd function, and cosine is even
sin (–t) = –sin t, and cos (–t) = cos t.
5.An obvious property of sines and cosines is that their values lie
between –1 and 1. Every point on the unit circle is 1 unit from the
origin, so the coordinates of any point are within 1 of 0 as well.

33. The Law(Rule) of sines
The Law of Sines is simple and beautiful and easy to derive. It’s
useful when you know two angles and any side of a triangle, or
sometimes when you know two sides and one angle.
Law of Sines — First Form:
a / sin A = b / sin B = c / sin C
This is very simple and beautiful: for any triangle, if you divide
any of the three sides by the sine of the opposite angle, you’ll get
the same result. This law is valid for any triangle.
Law of Sines— Second Form:
sin A / a = sin B / b = sin C / c

34. The Law(Rules) of cosines
The Law of Sines is fine when you can relate sides and angles. But
suppose you know three sides of the triangle — for instance
a = 180, b = 238, c = 340 — and you have to find the three angles.
The Law of Sines is no good for that because it relates two sides
and their opposite angles. If you don’t know any angles, you have
an equation with two unknowns and you can’t solve it.
 Law of Cosines — First Form:
cos A = (b² + c² − a²) / 2bc
cos B = (a² + c² − b²) / 2ac
cos C = (a² + b² − c²) / 2ab
Law of Cosines — Second Form:
a² = b² + c² − 2bc cos A
b² = a² + c² − 2ac cos B
c² = a² + b² − 2ab cos C

35. Trigonometric Equations
A formula that asserts that two expressions have the same value ;it is
either an identical equation or an identity which is true for any values of
the variables or a conditional equation which is only true for certain
values of the variables.
Example1
Solve the equation sin{1/3(θ-30)°} = √3/2, giving all the roots in the
interval 0°≤ θ ≤360°.
Example2
Find all the values of θ in the interval 0°≤ θ ≤360° for which
sin2θ = cos36°
Example3
Find all the values of θ in the interval 0°≤ θ ≤360° for which
sin2θ °-√ 3 cos2θ° = 0

36. Applications of Trigonometric Equations
Example
The height in meters of the water in a harbor is given by approximately
by the formula d=6+3cos30t° where t is the time measured in hours from
noon. Find the time after noon when the height of the water is 7.5 meters
for the second time.

37. THANK YOU
Mushtaq ur Rehman
H.O.D Mathematics Department
D.A.P.S. O&A Levels