Download to read offline
Uploaded byShenaz kheriwala
Trigonometry 1
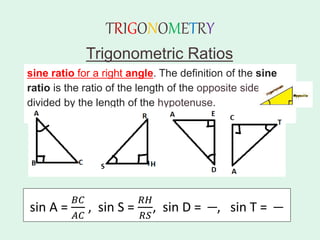
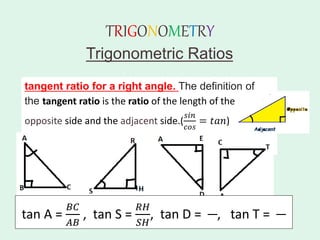
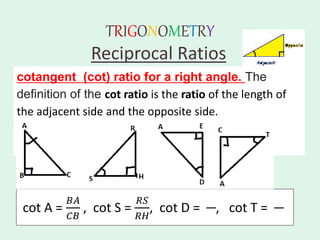
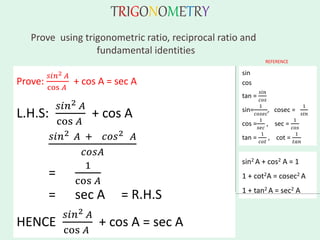
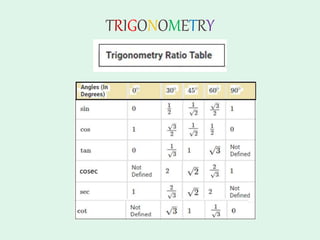
The document discusses trigonometry, covering essential concepts such as the six trigonometric ratios: sine, cosine, tangent, cosecant, secant, and cotangent, alongside their definitions related to right-angled triangles. It also presents fundamental identities and formulas for calculating relations among these ratios, providing examples and proofs for various trigonometric identities. The document serves as a comprehensive guide for understanding trigonometric functions and their applications.
More Related Content
Similar to Trigonometry 1
Trigonometry 1
- 1. TRIGONOMETRY-sk STD X MAHARASHTRA STATEBOARD OF EDUCATION, MUMBAI Trigonometric Ratios Reciprocal Ratios Fundamental Trigonometric Identities
- 2. TRIGONOMETRY Trigonometry is abranch of mathematics that studies relationships between side lengths and angles of triangles. There are six trigonometric ratios, sine, cosine, tangent, cosecant, secant and cotangent. These six trigonometric ratios are abbreviated as sin, cos, tan, cosec, sec, cot. These are referred to as ratios since they can be expressed in terms of the sides of a right-angled triangle for a specific angle θ.
- 3. TRIGONOMETRY Trigonometric Ratios sine ratiofor a right angle. The definition of the sine ratio is the ratio of the length of the opposite side divided by the length of the hypotenuse. sin A = 𝐵𝐶 𝐴𝐶 , sin S = 𝑅𝐻 𝑅𝑆 , sin D = , sin T =
- 4. TRIGONOMETRY cosine ratio fora right angle. The definition of the cosine ratio is the ratio of the length of the side adjacent to the angle divided by the length of the hypotenuse • Trigonometric Ratios cos A = 𝐴𝐵 𝐴𝐶 , cos S = 𝑆𝐻 𝑅𝑆 , cos D = , cos T =
- 5. TRIGONOMETRY tangent ratio fora right angle. The definition of the tangent ratio is the ratio of the length of the opposite side and the adjacent side.( 𝑠𝑖𝑛 𝑐𝑜𝑠 = 𝑡𝑎𝑛) Trigonometric Ratios tan A = 𝐵𝐶 𝐴𝐵 , tan S = 𝑅𝐻 𝑆𝐻 , tan D = , tan T =
- 6. TRIGONOMETRY cosecant (cosec) ratiofor a right angle. The definition of the cosec ratio is the ratio of the length of the hypotenuse divided by the length of the opposite side Reciprocal Ratios cosec A = 𝐴𝐶 𝐵𝐶 , cosec S = 𝑅𝑆 𝑅𝐻 , cosec D = , cosec T =
- 7. TRIGONOMETRY Reciprocal Ratios secant (sec)ratio for a right angle. The definition of the sec ratio is the ratio of the length of hypotenuse divided by the length of the side adjacent to the angle sec A = 𝐴𝐶 𝐴𝐵 , sec S = 𝑆𝑅 𝐻𝑆 , sec D = , sec T =
- 8. TRIGONOMETRY Reciprocal Ratios cotangent (cot)ratio for a right angle. The definition of the cot ratio is the ratio of the length of the adjacent side and the opposite side. cot A = 𝐵𝐴 𝐶𝐵 , cot S = 𝑅𝑆 𝑅𝐻 , cot D = , cot T =
- 9. TRIGONOMETRY FUNDAMENTAL TRIGONOMETRIC IDENTITIES sin2A + cos2 A = 1 1 + cot2A = cosec2 A 1 + tan2 A = sec2 A trigonometric ratio reciprocal ratio sin cosec cos sec tan cot
- 10. sin2 A +cos2 A = 1 1 + cot2A = cosec2 A 1 + tan2 A = sec2 A REFERENCE sin cos tan = 𝑠𝑖𝑛 𝑐𝑜𝑠 sin= 1 𝑐𝑜𝑠𝑒𝑐 , cosec = 1 𝑠𝑖𝑛 cos = 1 𝑠𝑒𝑐 , sec = 1 𝑐𝑜𝑠 tan = 1 𝑐𝑜𝑡 , cot = 1 𝑡𝑎𝑛
- 11. TRIGONOMETRY FUNDAMENTAL TRIGONOMETRIC IDENTITIES Ifsin A = 7 25 then find the value of cos A and tan A Sin2A + cos2 A =1 ( 7 25 )2 + cos2 A = 1 49 625 + cos2 A = 1 cos2A = 1- 49 625 cos2A = 625−49 625 cos2A = 576 625 cos A = 24 25 𝑠𝑖𝑛 𝑐𝑜𝑠 = tan 7 25 x 25 24 = tan A 7 24 = tan A
- 12. TRIGONOMETRY FUNDAMENTAL TRIGONOMETRIC IDENTITIES Iftan A = 3 4 then find the value of cos A and sec A 1 + tan2A = sec2 A 1 +( 3 4 )2 = sec2 A 1+ 9 16 =sec2 A 16+9 16 = sec2 A 25 16 = sec2 A 5 4 = sec A 1 sec 𝐴 = cos A cos A = 4 5
- 13. TRIGONOMETRY If 5 secA -12 cosec A = 0 then find the values of sec A, cos A and sin A 5 sec A -12 cosec A = 0 5 sec A = 12 cosec A sec 𝐴 𝑐𝑜𝑠𝑒𝑐 𝐴 = 12 5 1 𝑋 𝑠𝑖𝑛 𝐴 cos 𝐴 𝑋 1 = 12 5 tan A = 12 5
- 14. TRIGONOMETRY If tan A=1 then find the value of sin 𝐴+cos 𝐴 sec 𝐴+𝑐𝑜𝑠𝑒𝑐 𝐴 tan A = 1 but tan 450 = 1 hence, ∠𝐴 =450 Numerator: sin A + cos A sin 45 + cos 45 = 2( 1 2 ) = 2 1 2 x 2 2 = 2 ( 2 2 ) = 2 DENOMINATOR : sec A + cosec A sec 45 + cosec 45 = 2 + 2 = 2 2 𝑁 𝐷 = 2 2 2 = 1 2
- 15. TRIGONOMETRY Sin cos tan = 𝑠𝑖𝑛 𝑐𝑜𝑠 sin= 1 𝑐𝑜𝑠𝑒𝑐 , cosec= 1 𝑠𝑖𝑛 cos = 1 𝑠𝑒𝑐 , sec = 1 𝑐𝑜𝑠 tan = 1 𝑐𝑜𝑡 , cot = 1 𝑡𝑎𝑛 sin2 A + cos2 A = 1 1 + cot2A = cosec2 A 1 + tan2 A = sec2 A
- 16. TRIGONOMETRY Prove using trigonometricratio, reciprocal ratio and fundamental identities sin2 A + cos2 A = 1 1 + cot2A = cosec2 A 1 + tan2 A = sec2 A Prove: 𝑠𝑖𝑛2 𝐴 cos 𝐴 + cos A = sec A L.H.S: 𝑠𝑖𝑛2 𝐴 cos 𝐴 + cos A 𝑠𝑖𝑛2 𝐴 + 𝑐𝑜𝑠2 𝐴 𝑐𝑜𝑠𝐴 = 1 cos 𝐴 = sec A = R.H.S HENCE 𝑠𝑖𝑛2 𝐴 cos 𝐴 + cos A = sec A REFERENCE sin cos tan = 𝑠𝑖𝑛 𝑐𝑜𝑠 sin= 1 𝑐𝑜𝑠𝑒𝑐 , cosec = 1 𝑠𝑖𝑛 cos = 1 𝑠𝑒𝑐 , sec = 1 𝑐𝑜𝑠 tan = 1 𝑐𝑜𝑡 , cot = 1 𝑡𝑎𝑛
- 17. TRIGONOMETRY Prove using trigonometricratio, reciprocal ratio and fundamental identities PROVE: cos2 A (1 + tan2A) = 1 L.H.S: cos2 A (1 + tan2A) =cos2 A(sec2 A) = cos2 A ( 1 𝑐𝑜𝑠2 𝐴 ) =1 = R.H.S. Hence cos2 A (1 + tan2A) = 1 REFERENCE sin2 A + cos2 A = 1 1 + cot2A = cosec2 A 1 + tan2 A = sec2 A sin cos tan = 𝑠𝑖𝑛 𝑐𝑜𝑠 sin= 1 𝑐𝑜𝑠𝑒𝑐 , cosec = 1 𝑠𝑖𝑛 cos = 1 𝑠𝑒𝑐 , sec = 1 𝑐𝑜𝑠 tan = 1 𝑐𝑜𝑡 , cot = 1 𝑡𝑎𝑛
- 18. TRIGONOMETRY Prove using trigonometricratio, reciprocal ratio and fundamental identities PROVE: 𝟏−𝒔𝒊𝒏 𝑨 𝟏+𝒔𝒊𝒏 𝑨 = sec A – tan A L.H.S : (1−sin 𝐴) 𝑥 (1−sin 𝐴) (1+sin 𝐴) 𝑋 (1−sin 𝐴) = (1−sin 𝐴)2 1−𝑠𝑖𝑛2 = (1−sin 𝐴)2 𝑐𝑜𝑠2 𝐴 = 1−sin 𝐴 cos 𝐴 = 1 cos 𝐴 - sin 𝐴 cos 𝐴 =sec A – tan A = R.H.S REFERENCE sin2 A + cos2 A = 1 1 + cot2A = cosec2 A 1 + tan2 A = sec2 A sin cos tan = 𝑠𝑖𝑛 𝑐𝑜𝑠 sin= 1 𝑐𝑜𝑠𝑒𝑐 , cosec = 1 𝑠𝑖𝑛 cos = 1 𝑠𝑒𝑐 , sec = 1 𝑐𝑜𝑠 tan = 1 𝑐𝑜𝑡 , cot = 1 𝑡𝑎𝑛
- 19. TRIGONOMETRYProve using trigonometricratio, reciprocal ratio and fundamental identities REFERENCE PROVE: 1 sec 𝐴 −tan 𝐴 = se c A + tan A L.H.S: 1 sec 𝐴 −tan 𝐴 1 sec 𝐴 −tan 𝐴 X sec 𝐴+tan 𝐴 sec 𝐴+tan 𝐴 sec 𝐴+tan 𝐴 𝑠𝑒𝑐2 𝐴−𝑡𝑎𝑛2 𝐴 =sec 𝐴 + tan 𝐴 sin2 A + cos2 A = 1 1 + cot2A = cosec2 A 1 + tan2 A = sec2 A sin cos tan = 𝑠𝑖𝑛 𝑐𝑜𝑠 sin= 1 𝑐𝑜𝑠𝑒𝑐 , cosec = 1 𝑠𝑖𝑛 cos = 1 𝑠𝑒𝑐 , sec = 1 𝑐𝑜𝑠 tan = 1 𝑐𝑜𝑡 , cot = 1 𝑡𝑎𝑛
- 20. TRIGONOMETRYProve using trigonometricratio, reciprocal ratio and fundamental identities PROVE: (sec A – cos A)(cot A + tan A) = tan A sec A L.H.S: (sec A – cos A)(cot A + tan A) = ( 1 cos 𝐴 - cos A) ( cos 𝐴 sin 𝐴 + sin 𝐴 cos 𝐴 ) = ( 1− 𝑐𝑜𝑠2 cos 𝐴 ) ( 𝑐𝑜𝑠2 𝐴 +𝑠𝑖𝑛2 𝐴 sin 𝐴 . cos 𝐴 ) = 𝑠𝑖𝑛2 𝐴 cos 𝐴 x 1 𝑠𝑖𝑛𝐴 cos 𝐴 = sin 𝐴 cos 𝐴 x 1 cos 𝐴 = tanA X sec A REFERENCE sin2 A + cos2 A = 1 1 + cot2A = cosec2 A 1 + tan2 A = sec2 A sin cos tan = 𝑠𝑖𝑛 𝑐𝑜𝑠 sin= 1 𝑐𝑜𝑠𝑒𝑐 , cosec = 1 𝑠𝑖𝑛 cos = 1 𝑠𝑒𝑐 , sec = 1 𝑐𝑜𝑠 tan = 1 𝑐𝑜𝑡 , cot = 1 𝑡𝑎𝑛
- 21. TRIGONOMETRYProve using trigonometricratio, reciprocal ratio and fundamental identities PROVE: cot A + tan A = cosec A sec A L.H.S: cot A + tan A ( cos 𝐴 sin 𝐴 + sin 𝐴 cos 𝐴 ) = ( 𝑐𝑜𝑠2 𝐴 +𝑠𝑖𝑛2 𝐴 sin 𝐴 . cos 𝐴 ) = 1 𝑠𝑖𝑛𝐴 cos 𝐴 = 1 sin 𝐴 x 1 cos 𝐴 = cosec A sec A = R.H.S. REFERENCE sin2 A + cos2 A = 1 1 + cot2A = cosec2 A 1 + tan2 A = sec2 A sin cos tan = 𝑠𝑖𝑛 𝑐𝑜𝑠 sin= 1 𝑐𝑜𝑠𝑒𝑐 , cosec = 1 𝑠𝑖𝑛 cos = 1 𝑠𝑒𝑐 , sec = 1 𝑐𝑜𝑠 tan = 1 𝑐𝑜𝑡 , cot = 1 𝑡𝑎𝑛
- 22. TRIGONOMETRY Prove using trigonometricratio, reciprocal ratio and fundamental identities REFERENCE PROVE: sec A + tan A = cos 𝐴 1−sin 𝐴 L.H.S: sec A + tan A = 1 𝐶𝑂𝑆 𝐴 + 𝑆𝑖𝑛 𝐴 cos 𝐴 = 1+sin 𝐴 cos 𝐴 = 1+sin 𝐴 cos 𝐴 x 1−sin 𝐴 1−sin 𝐴 = 1−𝑠𝑖𝑛2 cos 𝐴 (1−sin 𝐴) = 𝑐𝑜𝑠2 𝐴 cos 𝐴 (1−sin 𝐴) = cos 𝐴 (1−sin 𝐴) = R.H.S. sin2 A + cos2 A = 1 1 + cot2A = cosec2 A 1 + tan2 A = sec2 A sin cos tan = 𝑠𝑖𝑛 𝑐𝑜𝑠 sin= 1 𝑐𝑜𝑠𝑒𝑐 , cosec = 1 𝑠𝑖𝑛 cos = 1 𝑠𝑒𝑐 , sec = 1 𝑐𝑜𝑠 tan = 1 𝑐𝑜𝑡 , cot = 1 𝑡𝑎𝑛
- 23. TRIGONOMETRY Prove using trigonometricratio, reciprocal ratio and fundamental identities sin2 A + cos2 A = 1 1 + cot2A = cosec2 A 1 + tan2 A = sec2 A sin cos tan = 𝑠𝑖𝑛 𝑐𝑜𝑠 sin= 1 𝑐𝑜𝑠𝑒𝑐 , cosec = 1 𝑠𝑖𝑛 cos = 1 𝑠𝑒𝑐 , sec = 1 𝑐𝑜𝑠 tan = 1 𝑐𝑜𝑡 , cot = 1 𝑡𝑎𝑛 PROVE: 1 + tan2 A = 1 𝑐𝑜𝑠2 𝐴 LHS 1 + tan2 A = sec2A = 1 𝑐𝑜𝑠2 𝐴 LHS 1 + tan2 A = 1 + 𝑠𝑖𝑛2 𝑐𝑜𝑠2 = 𝑐𝑜𝑠2 + 𝑠𝑖𝑛2 𝑐𝑜𝑠2 = 1 𝑐𝑜𝑠2
- 24. TRIGONOMETRY Prove using trigonometricratio, reciprocal ratio and fundamental identities sin2 A + cos2 A = 1 1 + cot2A = cosec2 A 1 + tan2 A = sec2 A sin cos tan = 𝑠𝑖𝑛 𝑐𝑜𝑠 sin= 1 𝑐𝑜𝑠𝑒𝑐 , cosec = 1 𝑠𝑖𝑛 cos = 1 𝑠𝑒𝑐 , sec = 1 𝑐𝑜𝑠 tan = 1 𝑐𝑜𝑡 , cot = 1 𝑡𝑎𝑛 PROVE: cot2 A - 1 𝑠𝑖𝑛2 𝐴 = -1 LHS cot2 A - 1 𝑠𝑖𝑛2 𝐴 = cot2A – cosec2A = -(cosec2A - cot2A) = -1
- 25. TRIGONOMETRY Prove using trigonometricratio, reciprocal ratio and fundamental identities PROVE: sec4A (1-sin4A)-2tan2A = 1 L.H.S: sec4A (1-sin4A)-2tan2A = sec4A (1-sin2A)(1 + sin2A) -2tan2A = sec4A cos2A (1 + sin2A) -2tan2A = 1 𝑐𝑜𝑠4 𝐴 cos2A (1 + sin2A) -2 𝑠𝑖𝑛2 𝐴 𝑐𝑜𝑠2 𝐴 = 1 + sin2 A 𝑐𝑜𝑠2 𝐴 -2 𝑠𝑖𝑛2 𝐴 𝑐𝑜𝑠2 𝐴 = 1−𝑠𝑖𝑛2 𝐴 𝑐𝑜𝑠2 𝐴 = 𝑐𝑜𝑠2 𝐴 𝑐𝑜𝑠2 𝐴 =1 = R.H.S sin2 A + cos2 A = 1 1 + cot2A = cosec2 A 1 + tan2 A = sec2 A sin cos tan = 𝑠𝑖𝑛 𝑐𝑜𝑠 sin= 1 𝑐𝑜𝑠𝑒𝑐 , cosec = 1 𝑠𝑖𝑛 cos = 1 𝑠𝑒𝑐 , sec = 1 𝑐𝑜𝑠 tan = 1 𝑐𝑜𝑡 , cot = 1 𝑡𝑎𝑛
- 26. TRIGONOMETRY PROVE: tan 𝐴 sec 𝐴−1 = tan𝐴+sec 𝐴+1 tan 𝐴+sec 𝐴−1 L.H.S: tan 𝐴 sec 𝐴−1 tan 𝐴 sec 𝐴−1 = tan 𝐴 sec 𝐴−1 X sec 𝐴+1 sec 𝐴+1 tan 𝐴 sec 𝐴−1 = tan 𝐴 (sec 𝐴+1) 𝑠𝑒𝑐2 𝐴−1 tan 𝐴 sec 𝐴−1 = tan 𝐴 (sec 𝐴+1) 𝑡𝑎𝑛2 𝐴 tan 𝐴 sec 𝐴−1 = (sec 𝐴+1) 𝑡𝑎𝑛 𝐴 = k Using property of equal ratio tan 𝐴+sec 𝐴+1 tan 𝐴 +sec 𝐴−1 = k = R.H.S HENCE tan 𝐴 sec 𝐴−1 = tan 𝐴+sec 𝐴+1 tan 𝐴+sec 𝐴=1 sin2 A + cos2 A = 1 1 + cot2A = cosec2 A 1 + tan2 A = sec2 A sin cos tan = 𝑠𝑖𝑛 𝑐𝑜𝑠 sin= 1 𝑐𝑜𝑠𝑒𝑐 , cosec = 1 𝑠𝑖𝑛 cos = 1 𝑠𝑒𝑐 , sec = 1 𝑐𝑜𝑠 tan = 1 𝑐𝑜𝑡 , cot = 1 𝑡𝑎𝑛
- 27. TRIGONOMETRY Prove: (cos A+ sin A)2 + (cos A -sin A)2 = 4cos A sin A LHS: (cos A +sin A)2 + (cosA -sin A)2 = (cos2A + 2cosA SinA + sin2A) - (cos2A - 2cosA SinA + sin2A) =cos2A + 2cosA sinA + sin2A -cos2A + 2cosA sinA - sin2A = 4cos A sin A Prove using trigonometric ratio, reciprocal ratio and fundamental identities
- 28.
- 29. sin2 A +cos2 A = 1 1 + cot2A = cosec2 A 1 + tan2 A = sec2 A sin cos tan = 𝑠𝑖𝑛 𝑐𝑜𝑠 sin= 1 𝑐𝑜𝑠𝑒𝑐 , cosec = 1 𝑠𝑖𝑛 cos = 1 𝑠𝑒𝑐 , sec = 1 𝑐𝑜𝑠 tan = 1 𝑐𝑜𝑡 , cot = 1 𝑡𝑎𝑛 THANK YOU trigonometric ratio reciprocal ratio sin cosec cos sec tan cot sin A = 𝐵𝐶 𝐴𝐶 , sin S = 𝑅𝐻 𝑅𝑆 , sin D = , sin T = cos A = 𝐴𝐵 𝐴𝐶 , cos S = 𝑆𝐻 𝑅𝑆 , cos D = , cos T = tan A = 𝐵𝐶 𝐴𝐵 , tan S = 𝑅𝐻 𝑆𝐻 , tan D = , tan T = cosec A = 𝐴𝐶 𝐵𝐶 , cosec S = 𝑅𝑆 𝑅𝐻 , cosec D = , cosec T = cot A = 𝐵𝐴 𝐶𝐵 , cot S = 𝑅𝑆 𝑅𝐻 , cot D = , cot T = sec A = 𝐴𝐶 𝐴𝐵 , sec S = 𝑆𝑅 𝐻𝑆 , sec D = , sec T =