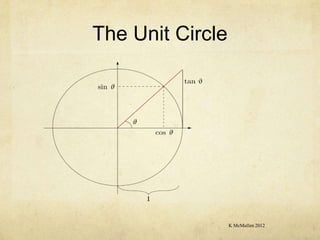
The document discusses the unit circle and trigonometric functions. It explains that the unit circle has a radius of 1 unit and is used to define trigonometric ratios. The horizontal and vertical sides of angles drawn on the unit circle give the cosine and sine of that angle. It also discusses converting between radians and degrees, symmetry of trig functions in different quadrants, trigonometric identities, and complementary angles.

1. Maths Methods
Trigonometric equations
K McMullen 2012

2. The Unit Circle
To help us understand the unit circle let’s first
look at the right-angled triangle with a
hypotenuse of 1 unit in length. The reason why it
is 1 unit is because we consider the
circumference of the circle to be 2π
(circumference of a circle is 2πr, therefore r=1
which is the hypotenuse) this will be explained in
more detail later.
K McMullen 2012

3. The Unit Circle
Using the cosine ratio in the triangle:
cosϑ=a/1
a=cosϑ
Using the sine ratio in the triangle:
sinϑ=b/1
b=sinϑ
This means that in a unit circle the horizontal length in the measure
of the cosine of the angle and the vertical length is a measure of the
sine of the angle.
K McMullen 2012

4. The Unit Circle
When this triangle is places inside a circle, it can
be used to find the trig ratios shown preiviously.
The value of cosϑ can be read off the x-axis.
The value of sinϑ can be read off the y-axis.
The value of tanϑ can be read off a vertical
tangent line drawn on the right side of the
unit circle.
A copy of the unit circle is in the next slide
K McMullen 2012

5. The Unit Circle
K McMullen 2012

6. Converting between radians and
degrees
Angles are measured in degrees or radians.
To define a radian we can use a circle which has a
radius of one unit. This circle is called the unit circle.
When working with degrees we know that one
revolution of a circle is 360°. When working with
radians one revolution is 2π (this is because we are
working with a circle with a radius of 1).
Therefore:
360°=2π
180°=π
K McMullen 2012

7. Converting between radians
and degrees
The radius of the circle can be any length and can still be
regarded as a unit. As long as the arc is the same length
as the radius, the angle will always measure one radian.
An angle of 1 degree can be denoted as 1°.
A radian angle can be denoted as 1c but we usually leave
off the radian sign.
Therefore,
1c=180°π 1°=π180
K McMullen 2012

8. Converting between radians
and degrees
Always make sure your calculator is in radian
mode when working with radians and degree
mode when working with degrees.
When working with radians and the unit circle we
are no longer referring to North, East, South and
West like we would with a compass. With the unit
circle we use a set of axes (the Cartesian plane)
with the x-axis as the horizontal and the y-axis as
the vertical. Remember that cosϑ=x and sinϑ=y.
K McMullen 2012

9. Converting between radians
and degrees
Below is a copy of the unit circle. You need to
familiarize yourself with the values from this unit
circle so make sure you remember the table of
exact values that we did previously (it’s easy to
recalculate these if needed by simply redrawing
the two triangles).
K McMullen 2012

10. K McMullen 2012

11. Exact Values
Using the equilateral triangle (of side length 2 units), the following
exact values can be found:
(look at page 271 to get the exact values- these go to the right of each ‘=‘
sign)
sin30°=sinπ/6=
sin60°=sinπ/3=
cos30°=cosπ/6=
cos60°=cosπ/3=
tan30°=tanπ/6=
tan60°=tanπ/3=
K McMullen 2012

12. Exact Values
Using the right isosceles triangle with two sides
of length 1 unit, the following exact values can be
found:
sin45°=sinπ/4=
cos45°=cosπ/4=
tan45°=tanπ/4=
K McMullen 2012

13. Symmetry Formulae
The unit circle is symmetrical so that the
magnitude of sine, cosine and tangent at the
angles shown are the same in each quadrant but
the sign varies.
We’ll go over this in more detail in class
K McMullen 2012

14. Trigonometric Identities
When a right-angled triangle is placed in the first
quadrant of a unit circle, the horizontal side has the
length of cosϑ and the vertical side has the length of
sinϑ.
Therefore, using the tan ratio
(tanϑ=opposite/adjacent):
tanϑ=sinϑ/cosϑ
Using Pythagoras’ theorem (a2+b2=c2):
(sinϑ)2+(cosϑ)2=12
sin2ϑ+cos2ϑ=1
K McMullen 2012

15. Complementary Angles
Complementary angles add to 90° or π/2 radians.
Therefore, 30° and 60° are complementary angles. In
other words π/6 and π/3 are complementary
angles, and θ and π/2-θ are also complementary
angles.
The sine of an angle is equal to the cosine of its
complement. Therefore, sin60°=cos(30°). We say that
sine and cosine are complementary functions.
The complement of the tangent of an angle is the
cotangent or cot- that is, tangent and cotangent are
complementary functions (as well as reciprocal
functions).
K McMullen 2012

16. Complementary Angles
Copy the table from page 270 into your notes
K McMullen 2012