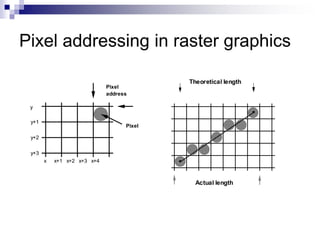
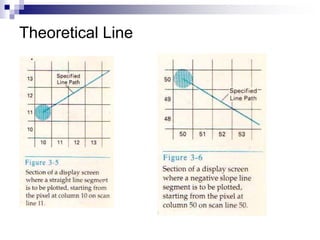
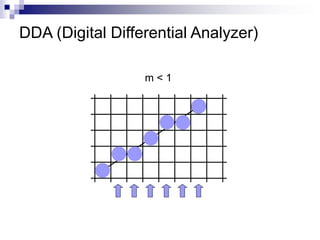
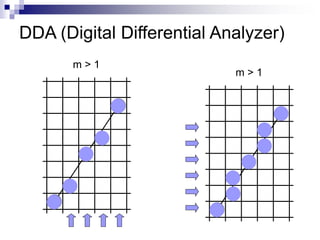
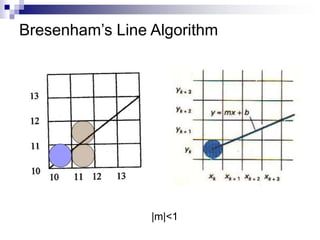
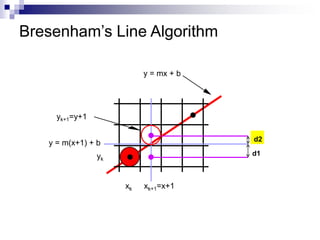
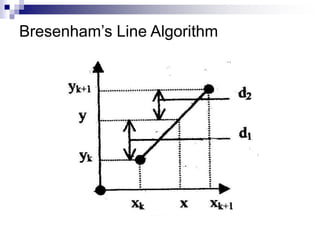
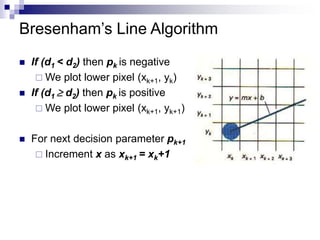
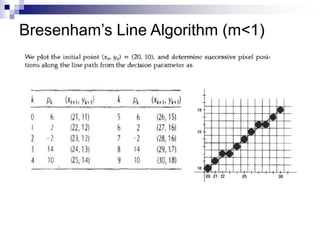
The document outlines the fundamental concepts of graphics primitives, including point and line plotting techniques in computer graphics. It explains algorithms such as Digital Differential Analyzer (DDA) and Bresenham's line algorithm used for efficient rasterization of geometric shapes. It emphasizes the importance of these algorithms in creating visually satisfactory images while maintaining performance in interactive graphics.

1. Scan Conversion
Dept of Computer Science & Engineering
Islamic University, Kushtia

2. Graphics Primitives
 The basic building blocks for pictures are referred to as output
primitives.
 They include:
 character strings and
 geometric entities,
 Points,
 Straight lines,
 Curved Lines,
 Circle, Ellipse
 Filled areas (polygons, circles, etc.), and
 Shapes defined with arrays of color points.
 Routines for generating output primitives provide the basic
tools for constructing pictures.

3. Coordinates

4. Pixel addressing in raster graphics
Pixel
address
Pixel
x x+1 x+2 x+3 x+4
y
y+1
y+2
y+3
Theoretical length
Actual length

5. POINTS AND LINES
 Point plotting is accomplished by converting a single
coordinate position furnished by an application program
into appropriate operations for the output device in use.
 For example, CRT monitor, the electron beam is
turned on to illuminate the screen phosphor at the
selected location

6. POINTS AND LINES
 Line drawing is accomplished by calculating
intermediate positions along the line path
between two specified endpoint positions.
 Digital devices display a straight line segment by
plotting discrete points between the two
endpoints.
Discrete coordinate positions along the line
path are calculated from the equation of the
line.

7. Theoretical Line

8. Line on Display Devices

9. Line drawing algorithms
 Geometric
 Display devices
 DDA
 Bresenham

10. Line drawing algorithms
 The Cartesian slope-intercept
equation for a straight line is
 with m representing the slope of
the line and b as they intercept

11. Line drawing algorithms
 Problems in Geometric Equations:
 To plot a line need
 Multiplication, Division or more complex task
 Computer needs lot of task
 This degrade overall performance
 Interactive graphics need faster response
 Use DDA, Bresenham’s algorithm
 Interactive Graphics: where user dynamically controls
the presentation of graphics model on a computer
display

12. Requirements
1. Must compute integer coordinates of pixels which lie on or
near a line or circle.
2. Pixel level algorithms are invoked hundreds or thousands of
times when an image is created or modified.
3. Lines must create visually satisfactory images.
 Lines should appear straight
 Lines should terminate accurately
 Lines should have constant density
 Line density should be independent of line length and
angle.
4. Line algorithm should always be defined.

13. DDA (Digital Differential Analyzer)
m < 1

14. DDA (Digital Differential Analyzer)
m > 1
m > 1

15. DDA Algorithms
 DDA is a scan-conversion line algorithm based on
calculating either y or x
 If the slope is less than or equal to 1, we sample at unit x
intervals ( x = 1) and compute each successive y value
as
where k=1 for first point and increases by 1until the final
endpoint is reached
 Calculated y values must be rounded to the nearest
integer

16. DDA Algorithms
 For lines with a positive slope greater than 1, reverse the
roles of x and y.
 we sample at unit y intervals (y = 1) and calculate
each succeeding x value as
equation (a) and (b) are based on the assumption that
lines are to be processed from the left endpoint to the
right endpoint

17. DDA Algorithms
 If this processing is reversed, that is from right to left
 The DDA algorithm is a faster method for calculating
pixel positions than the direct use
 It eliminates the multiplication by making use of raster
characteristics

18. DDA at a glance
 input line endpoints, (x1,y1) and (x2, y2)
 set pixel at position (x1,y1)
 calculate slope m
 Case |m|≤1: repeat the following steps until (x2, y2) is
reached:
yi+1 = yi + y/ x
xi+1 = xi + 1
set pixel at position (xi+1,Round(yi+1))
 Case |m|>1: repeat the following steps until (x2, y2) is
reached:
xi+1 = xi + x/ y
yi+1 = yi + 1
set pixel at position (Round(xi+1), yi+1)

19. Bresenham’s Line Algorithm
 Bresenham’s scan converts lines using only incremental
integer calculations that can be adapted to display
circles and other curves.
|m|<1 |m|>1

20. Bresenham’s Line Algorithm
|m|<1

21. Bresenham’s Line Algorithm (m<1)
 Starting from the left endpoint (x0, y0) of a given line,
 We step to each successive column (x position) and
 Plot the pixel whose scan-line y value is closest to the
line path.
 Let we have determined the pixel at (xk, yk) to be
displayed,
 we next need to decide which pixel to plot in column
xk+1,
 Our choices are the pixels at positions (xk+1, yk) and
(xk+1, yk+1)

22. Bresenham’s Line Algorithm
d1
d2
xk xk+1=x+1
yk
y = m(x+1) + b
y = mx + b
yk+1=y+1

23. Bresenham’s Line Algorithm

24. Bresenham’s Line Algorithm
 They coordinate on the mathematical line at pixel column
position xk+1 is calculated as
 The difference between these two separations is

25. Bresenham’s Line Algorithm
where pk = x(d1 – d2) is decision parameter for the kth
step in the line algorithm
The sign of p, is the same as the sign of (d1 – d2) since
x > 0
and c is constant and c = 2y + x(2b – 1),

26. Bresenham’s Line Algorithm
 If (d1 < d2) then pk is negative
 We plot lower pixel (xk+1, yk)
 If (d1  d2) then pk is positive
 We plot lower pixel (xk+1, yk+1)
 For next decision parameter pk+1
 Increment x as xk+1 = xk+1

27. Bresenham’s Line Algorithm
 The term (yk+1–yk) of eq-(f) either 0 or 1 depending on
sign of pk

28. Bresenham’s Line Algorithm
 If pk < 0 true line close to lower pixel and yk +1 = yk
pk+1 = pk + 2y -- g(a)
 If pk  0 true line close to lower pixel and yk +1 = yk+1
pk+1 = pk + 2y – 2x -- g(b)
 First decision parameter p0 from eq-(d) as considering the line
start from (0, 0) as
p0 = 2y.0 – 2x.0 + c
p0 = c = 2y + x(2b – 1)
but y = mx + b or b = 0
p0 = 2y - x

29. Bresenham’s Line Algorithm (m<1)

30. Bresenham’s Line Algorithm (m<1)

31. Bresenham’s Line Algorithm (m<1)

32. Bresenham’s Line Algorithm