Đề thi thử đại học năm 2010 - 2011 môn Toán gồm nhiều câu hỏi về khảo sát hàm số, giải phương trình, tính tích phân, và hình học. Các câu hỏi yêu cầu thí sinh thực hiện khảo sát, chứng minh, tính toán và giải hệ phương trình, với tổng điểm là 10. Thí sinh không được sử dụng tài liệu trong suốt thời gian thi.

1. TRƯỜNG THPT TRẦN PHÚ
TỔ TOÁN ­ TIN
ĐỀ THI THỬ ĐẠI HỌC NĂM HỌC 2010 ­ 2011
Môn: TOÁN ­ Khối A + B
Ngày thi: 28/12/2010
Thời gian làm bài: 180 phút
(không kể thời gian giao đề)
Câu I. (2,0 điểm) Cho hàm số y x x4 2
5 4,= - + có đồ thị (C).
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2. Tìm m để phương trình x x m4 2
25 4 log- + = có 6 nghiệm phân biệt.
Câu II. (2,0 điểm)
1. Giải phương trình: 1
cos 1
sin 2 ) 1 cos 2 ( cos 1
=
-
-+-
x
x x x
2. Giải hệ phương trình :
2
4 2 2
1
log log 16 4
log 2
4 8 16 4
xy
y
x
x x xy x x y
ì
+ = -ï
í
ï + + = +î
Câu III. (2,0 điểm)
1. Tính tích phân: I =
4
2
0
( sin 2 )cos2 x x xdx
p
+ò .
2. Tìm m để hệ phương trình sau có nghiệm:
2
3 2
3 4 0
3 15 0
x x
x x x m m
ì - - £ï
í
- - - ³ïî
Câu IV. (1,0 điểm) Cho lăng trụ tam giác ABC.A'B'C' có đáy ABC là tam giác đều
cạnh a . Hình chiếu của A' xuống mặt phẳng (ABC) là tâm O đường tròn ngoại tiếp tam
giác ABC. Biết AA' hợp với mặt phẳng đáy (ABC) một góc 60 .
1. Chứng minh rằng BB'C'C là hình chữ nhật.
2. Tính thể tích khối lăng trụ .
Câu V (2,0 điểm)
1. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC với 5 AB = , C(­1;­1),
đường thẳng AB có phương trình: x + 2y – 3 = 0 và trọng tâm tam giác ABC thuộc
đường thẳng x + y – 2 = 0. Tìm tọa độ đỉnh A và B.
2. Giải bất phương trình:
2 2
2 1 2 1 4
(2 3) (2 3)
2 3
x x x x- + - -
+ + - £
-
Câu VI. (1,0 điểm) Tính tổng: S =
0 1 2 2010
2010 2010 2010 2010 2 3 ... 2011 C C C C+ + + + .
.........….. Hết …...........
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: ………………………………………………; Số báo danh: ………..
http://laisac.page.tl
Thi th Đ i h c www.toanpt.net

2. ĐÁP ÁN ĐỀ THI THỬ ĐẠI HỌC ­ NĂM: 2010 ­2011
CÂU NỘI DUNG ĐIỂM
* Tập xác định D = R
* Sự biến thiên:
­ Chiều biến thiên: y’ = 4x 3
­ 10x = 2x(2x 2
­ 5); y’ = 0 Û
0
5
2
=é
ê
ê = ±
êë
x
x
.
Dấu của y’:
x ­¥
5
2
- 0
5
2
+¥
y’ ­ 0 + 0 ­ 0 +
Hàm số nghịch biến trên các khoảng (­ ¥; ­
5
2
) và (0;
5
2
).
Hàm số đồng biến trên các khoảng (­
5
2
; 0) và (
5
2
; + ¥).
­ Cực trị:
+ Hàm số đạt cực tiểu tại x = ±
5
2
, yCT = ­
9
4
; Hàm số đạt cực đại tại x = 0, yCĐ = 4.
0,25
­ Giới hạn: 4
2 4
5 4
lim lim (1 )
x x
y x
x x®±¥ ®±¥
= - + = +¥ . 0,25
­Bảng biến thiên:
x ­¥
5
2
- 0
5
2
+¥
y’ ­ 0 + 0 ­ 0 +
y
+¥
­
9
4
4
­
9
4
+¥
0,25
I­1
(1
điểm)
Đồ thị:
­ Đồ thị hàm số cắt trục Ox tại điểm:
(­1;0), (1; 0), (­2; 0), (2; 0)
­ Đồ thị hàm số cắt trục Oy tại điểm (0; 0)
­ Đồ thị hàm số nhận trục tung làm trục đối xứng.
0,25
Số nghiệm của phương trình: x x m4 2
25 4 log- + = là số giao điểm của đường thẳng y
= 2 log m với đồ thị của hàm số = - +y x x4 2
5 4 .
0,25
Vẽ được đồ thị hàm số = - +y x x4 2
5 4
0,25
Xác định được điều kiện: < < Û < <m m20 log 4 1 16 0,25
I­2
(1
điểm)
Kết luận m Î(1; 16). 0,25
5
4
3
2
1
1
2
3
2 2
6
5
4
3
2
1
1
2 2
Thi th Đ i h c www.toanpt.net

3. + ĐK : p 2 1 cos m x x ¹Û¹ 0,25
(2)
0 sin 2 ) sin 1 ( 2 cos 1 sin 2 cos cos 2 1 2 2
=---Û-=---Û x x x x x x
2 sin
2
2
sin 0 2 sin 2 sin 2 2
=Ú-=Û=--Û x x x x (loại)
0,5
ê
ê
ê
ê
ë
é
+=
+-=
Û÷
ø
ö
ç
è
æ
-=-=
p
p
p
p
p
2
4
5
2
4
4
sin
2
2
sin
k x
k x
x 0,25
II­1
(1 điểm)
+) Từ PT (1) ta có: xy = 4. 0,25
+) Thế vào (2) ta có:
2
4 2 2 4 1 1
4 8 4 16 4 8 x x x x x x
x x x
æ ö
+ + = + Û + = +ç ÷
è ø
.
Đặt
1
x
x
+ (t > 0), ta có phương trình: t 4
= 8t Û t = 2 (vì t > 0).
Với t = 2 ta có: 2 1 1
2 4 4 1 0 x x x x
x x
+ = Û + = Û - + = 2 3xÛ = ±
0,25
0,25
II­2
(1 điểm)
+) KL : Hệ có các nghiệm là : 4 4
2 3; ; 2 3;
2 3 2 3
æ ö æ ö
+ -ç ÷ ç ÷
+ -è ø è ø
0,25
I =
4 4 4
2 2
1 2
0 0 0
( sin 2 )cos2 .cos2 sin 2 .cos2 x x xdx x xdx x xdx I I
p p p
+ = + = +ò ò ò .
+ Tính I1: Đặt: 1
cos2 sin 2
2
du dx
u x
dv xdx v x
=ì=ì ï
Þí í
= =î ïî
.
4
4 4
1
0
0 0
1 1 1 1
. sin 2 sin 2 cos2
2 2 8 4 8 4
I x x xdx x
p
p p
p p
Þ = - = + = -ò .
0,25
0,25
+ Tính I2:
4
2
0
sin 2 .cos2 x xdx
p
ò Đặt t = sin2x Þ dt = 2cos2xdx.
x = 0 Þ t = 0, x =
4
p
Þ t = 1.
Þ I2 =
1 3
2
0
1
0
1 1 1
.
2 2 3 6
t
t dx = =ò .
0,25
III ­ 1
(1 điểm)
Vậy I =
1
8 12
p
+ 0,25
III ­ 2
(1 điểm)
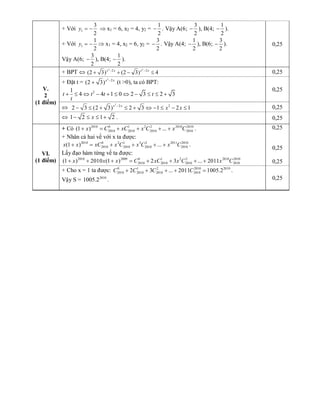
Ta có: 2
3 4 0 1 4 x x x- - £ Û - £ £ .
Hệ phương trình đã cho có nghiệm
Û PT 3 2
3 15 0 x x x m m- - - ³ có nghiệm [ ] 1;4 x Î -
3 2
3 15 x x x m mÛ - ³ + có nghiệm [ ] 1;4 x Î -
Đặt ( )
3 2
3
3 2
3 1 0
3
3 0 4
x x khi x
f x x x x
x x khi x
ì + - £ <ï
= - = í
- £ £ïî
0,25

4. Ta có : ( )
2
2
3 6 1 0
'
3 6 0 4
x x khi x
f x
x x khi x
ì + - < <ï
= í
- < <ïî
; ( ) ' 0 0; 2 f x x x= Û = = ±
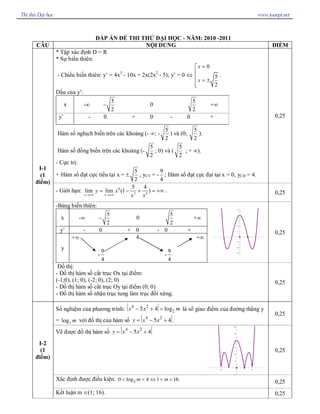
Ta có bảng biến thiên :
( ) 2
15 f x m m³ + có nghiệm [ ] 1;4 x Î -
[ ]
( ) 2
1;4
max 15 f x m m
-
Û ³ + 2
16 15 m mÛ ³ +
2
15 16 0 16 1 m m mÛ + - £ Û - £ £
Vậy hệ phương trình đã cho có nghiệm 16 1 mÛ - £ £ .
0,25
0,25
0,25
0,25
1. Ta có A'O (ABC) OA^ Þ là hình chiếu của AA'
trên (ABC).
Vậy ¼ o
góc[AA',(ABC)] OAA' 60= =
Ta có BB'CC' là hình bình hành ( vì mặt bên của lăng trụ)
AO BC^ tại trung điểm H của BC nên BC A'H^ .
BC (AA'H) BC AA'Þ ^ Þ ^ mà AA'//BB' nên
BC BB'^ .Vậy BB'CC' là hình chữ nhật.
0,25
0,25 IV
(1 điểm)
ABC V đều nên 2 2 a 3 a 3
AO AH
3 3 2 3
= = =
o AOA' A'O AOtan60 aÞ = =V
Vậy V = SABC.A'O =
3
a 3
4
0,25
0,25
Gọi A(x1; y1), B(x2; y2). Trọng tâm G của tam giác ABC có tọa độ là:
1 2 1 2 1 1
( ; )
3 3
x x y y
G
+ - + -
.
Có G thuộc đường thẳng x + y ­ 2 = 0 nên:
1 2 1 2
1 2 1 2
1 1
2 0 8
3 3
x x y y
x x y y
+ - + -
+ - = Û + + + = (1).
0,25
Có A, B thuộc đường thẳng : x + 2y – 3 = 0 nên 1 1
2 2
3 2
3 2
x y
x y
= -ì
í
= -î
(2), suy ra
1 2 1 2 2( ) 6 x x y y+ + + = (3).
Từ (1) và (3) suy ra: 1 2 2 1
1 2 2 1
10 10
2 2
x x x x
y y y y
+ = = -ì ì
Ûí í
+ = - = - -î î
0,25
V.
1
(1 điểm)
+ AB = 5 Û AB 2
= 5 Û 2 2
2 1 2 1 ( ) ( ) 5 x x y y- + - = Û 2 2
1 1 (10 2 ) ( 2 2 ) 5 x y- + - - =
Kết hợp với (2) ta được:
1
2 2
1 1
1
3
2 (4 4 ) ( 2 2 ) 5
1
2
y
y y
y
é
= -ê
+ + - - = Û ê
ê = -
êë
0,25
H
O
o 60
C'
A
a
B'
A'
C
B
x
f’(x)
f(x)
­1
+
4
­4
2
0 2
0 0 ­ ­
16

5. + Với 1
3
2
y = - Þ x1 = 6, x2 = 4, y2 =
1
2
- . Vậy A(6;
3
2
- ), B(4;
1
2
- ).
+ Với 1
1
2
y = - Þ x1 = 4, x2 = 6, y2 =
3
2
- . Vậy A(4;
1
2
- ), B(6;
3
2
- ).
Vậy A(6;
3
2
- ), B(4;
1
2
- ).
0,25
+ BPT Û
2 2
2 2
(2 3) (2 3) 4 x x x x- -
+ + - £ 0,25
+ Đặt t =
2
2
(2 3) x x-
+ (t >0), ta có BPT:
2 1
4 4 1 0 2 3 2 3 t t t t
t
+ £ Û - + £ Û - £ £ +
0,25
Û
2
2 2
2 3 (2 3) 2 3 1 2 1 x x
x x-
- £ + £ + Û - £ - £ 0,25
V.
2
(1 điểm)
Û 1 2 1 2 x- £ £ + . 0,25
+ Có 2010 0 1 2 2 2010 2010
2010 2010 2010 2010 (1 ) ... x C xC x C x C+ = + + + + .
+ Nhân cả hai vế với x ta được:
2010 0 2 1 3 2 2011 2010
2010 2010 2010 2010 (1 ) ... x x xC x C x C x C+ = + + + + .
Lấy đạo hàm từng vế ta được:
2010 2009 0 1 2 2 2010 2010
2010 2010 2010 2010 (1 ) 2010 (1 ) 2 3 ... 2011 x x x C xC x C x C+ + + = + + + +
0,25
0,25
0,25
VI.
(1 điểm)
+ Cho x = 1 ta được: 0 1 2 2010 2010
2010 2010 2010 2010 2 3 ... 2011 1005.2 C C C C+ + + + = .
Vậy S = 2010
1005.2 . 0,25