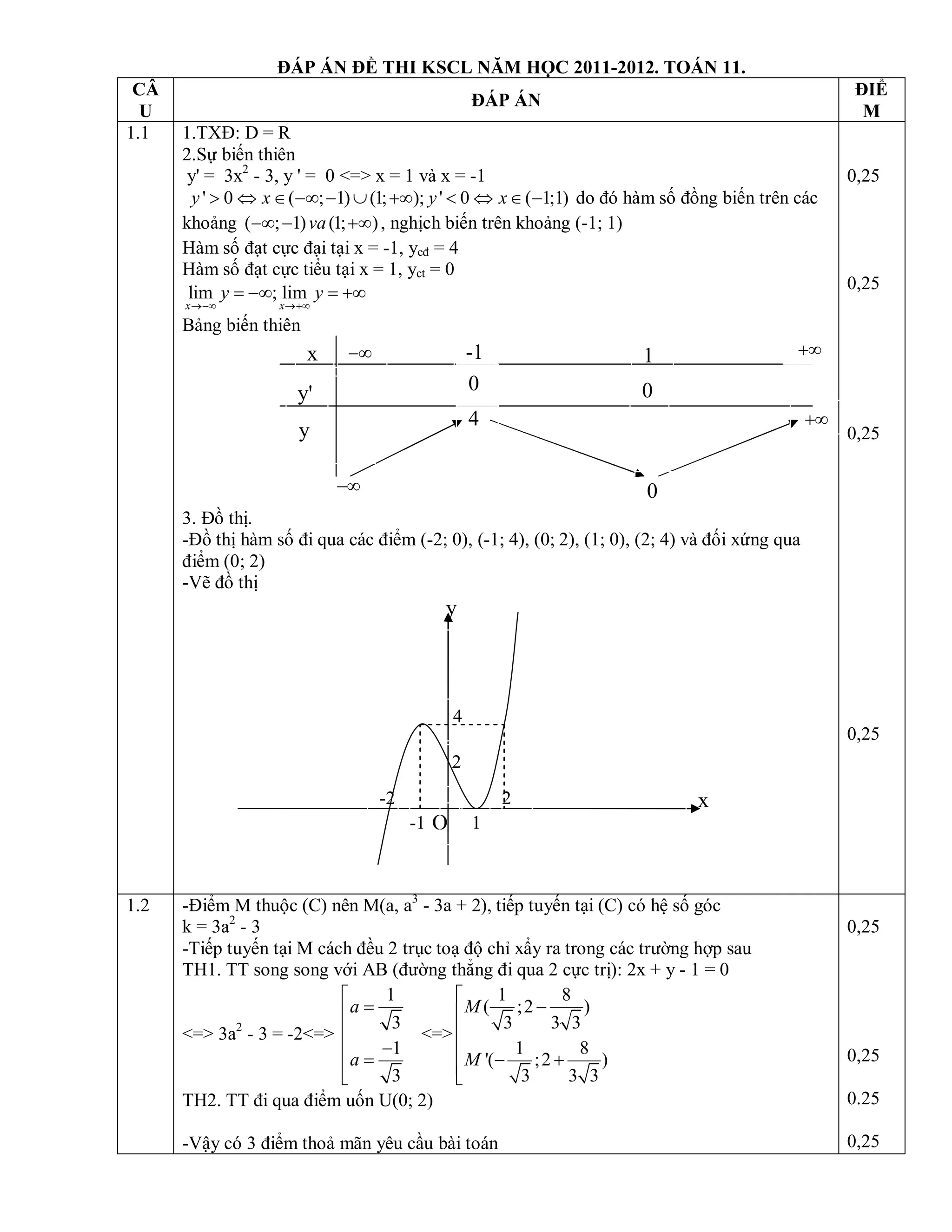
Tài liệu là đề thi toán cho thí sinh khối A, B, D năm học 2011-2012, gồm nhiều bài toán liên quan đến khảo sát hàm số, giải phương trình, tính tích phân và tính thể tích hình chóp. Đề thi chia thành hai phần: phần chung cho tất cả thí sinh và phần riêng theo chương trình chuẩn hoặc nâng cao. Thí sinh phải tuân thủ quy định không sử dụng tài liệu trong khi làm bài.

1. I PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7,0 điểm)
Câu I: (2,0 điểm) Cho hàm số : y = x 3
– 3x + 2
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2. Tìm trên đồ thị ( C) điểm M sao cho tiếp tuyến với ( C) tại M, cách đều hai điểm cực trị của
đồ thị hàm số
Câu II: (2,0 điểm)
1. Giải phương trình: 2tan2x + 2sin2x = 3cotx .
2. Giải phương trình:
3 3
2
3 2.3 3 2 0 x x x x x+ -
- - + =
Câu III: (1,0 điểm) Tính tích phân: I =
1 3 3
4
1
3
2012 x x x
dx
x
- +
ò
Câu IV: (1,0 điểm) Cho hình chóp S.ABC có đáy là tam giác vuông tại A, AB = 3, AC = 4 góc tạo
bởi các mặt bên và đáy bằng 60 o
. Tính thể tích của khối chóp S.ABC
Câu V: (1,0 điểm) Giải hệ phương trình sau: 2 2 2 2
2
2 2 3 1 0
4 2 2 0 x y x y
x xy x y
+ +
ì + - - + =ï
í
- - =ïî
II PHẦN RIÊNG (3,0 điểm) Thí sinh chỉ được làm một trong hai phần (phần A hoặc B).
A. Theo chương trình Chuẩn.
Câu VI.a (2,0 điểm)
1. Trong không gian toạ độ Oxyz, cho đường thẳng d :
3 1 5
1 2 4
x y z- - -
= = và điểm A(2;3;1) Viết
phương trình đường thẳng D đi qua điểm A cắt đường thẳng d và khoảng cách từ gốc tọa độ O đến D
là lớn nhất
2. Trong mặt phẳng hệ toạ độ Oxy cho ba đường d1: x – 2y + 1 = 0; d2: 3x – y – 2 = 0;
d3: 2x + y + 1 = 0. Tìm điểm M trên d1 điểm N trên d2 sao cho MN = 5 và MN song song với d3
CâuVII.a (1,0 điểm) Từ các số 0;1;2;3;4;5;6 có thể lập được bao nhiêu số tự nhiên có ba chữ số khác
nhau mà tổng của ba chữ số đó bằng 7
B. Theo chương trình Nâng cao.
Câu VI.b (2,0 điểm)
1. Trong mặt phẳng toạ độ Oxy, cho đường tròn (C) có phương trình:x 2
+ y 2
– x – 4y – 2 = 0 và các
điểm A(3 ;­5) ; B(7;­3). Tìm điểm M trên đường tròn (C ) sao cho P = MA 2
+ MB 2
nhỏ nhất
2. Trong không gian toạ độ Oxyz, cho mặt phẳng (P): x ­3y + 4z – 1 = 0 ; đường thăng
d:
1 3
1
2
x t
y t
z t
= +ì
ï
= - +í
ï =î
và điểm A(3;1;1) .Lập phương trình đường thẳng D đi qua A cắt đường thẳng d và
song song với mặt phẳng (P )
Câu VII.b (1,0 điểm) Tìm giới hạn sau: I = 2 x 0
1 cos2011x. cos 2012x
lim
x®
-
­­­­­­­­­­­­­­­­­­­­­­­­Hết­­­­­­­­­­­­­­­­­­­­­­
Thí sinh không được sử dụng tài liệu.Thí sinh khối D không phải làm câu V. Cán bộ coi thi
không giải thích gì thêm
TRƯỜNG THPT
YÊN THÀNH 2
KỲ THI THỬ ĐẠI HỌC LẦN THỨ NHẤT NĂM HỌC 2011 – 2012
ĐỀ THI MÔN: TOÁN KHỐI A, B, D
Thời gian làm bài: 180 phút, không kể thời gian giao đề
Thi thử Đại học www.toanpt.net

2. ĐÁP ÁN ĐỀ THI KSCL NĂM HỌC 2011­2012. TOÁN 11.
CÂ
U
ĐÁP ÁN
ĐIỂ
M
1.1 1.TXĐ: D = R
2.Sự biến thiên
y' = 3x 2
­ 3, y ' = 0 <=> x = 1 và x = ­1
' 0 ( ; 1) (1; ); ' 0 ( 1;1) y x y x> Û Î -¥ - È +¥ < Û Î - do đó hàm số đồng biến trên các
khoảng ( ; 1) (1; ) va-¥ - +¥ , nghịch biến trên khoảng (­1; 1)
Hàm số đạt cực đại tại x = ­1, ycđ = 4
Hàm số đạt cực tiểu tại x = 1, yct = 0
lim ; lim
x x
y y
®-¥ ®+¥
= -¥ = +¥
Bảng biến thiên
3. Đồ thị.
­Đồ thị hàm số đi qua các điểm (­2; 0), (­1; 4), (0; 2), (1; 0), (2; 4) và đối xứng qua
điểm (0; 2)
­Vẽ đồ thị
0,25
0,25
0,25
0,25
1.2 ­Điểm M thuộc (C) nên M(a, a 3
­ 3a + 2), tiếp tuyến tại (C) có hệ số góc
k = 3a 2
­ 3
­Tiếp tuyến tại M cách đều 2 trục toạ độ chỉ xẩy ra trong các trường hợp sau
TH1. TT song song với AB (đường thẳng đi qua 2 cực trị): 2x + y ­ 1 = 0
<=> 3a 2
­ 3 = ­2<=>
1
3
1
3
a
a
é
=ê
ê
-ê
=ê
ë
<=>
1 8
( ;2 )
3 3 3
1 8
'( ;2 )
3 3 3
M
M
é
-ê
ê
ê
- +ê
ë
TH2. TT đi qua điểm uốn U(0; 2)
­Vậy có 3 điểm thoả mãn yêu cầu bài toán
0,25
0,25
0.25
0,25
x
y'
y
4
0-¥
+¥
­1 1
0 0
-¥ +¥
1
4
y
x
O
­2
­1
2
2

3. 2.1
­ĐK
os2 0
sinx 0
c x ¹ì
í
¹î
­
2
2
2sin 2 (1 os2 ).sinx 3cos . os2 2sin 2 .cos 3cos . os2
2
2 cos 0
os2 2
6 2 os 2 3 os2 2 0
1
os2
2
6
pt x c x x c x x x x c x
x k
x k
x
c x x n
c x c x
c x
x m
p
p p
p
p
p
p
p
Û + = Û =
é
= +é ê= +ê ê
=é ê êÛ Û = - Û = +ê ê ê+ - =ë ê ê
-=ê ê = +ë êë
­Đối chiếu điều kiện ta thấy pt có 3 họ nghiệm:...
0,25
0,5
0,25
2.2 3 3 3 3
3 3 3 3 3
3
3
3 2.3 3 .3 2 0
3 (1 3 ) 2(1 3 ) 0 (1 3 )(2 3 ) 0
3 1 0
1 3 2 0( )
x x x x x x x x
x x x x x x x x x x
x x
x x
pt
x
x VN
+ - - +
+ - - - +
-
+
Û - - + =
Û - + - = Û - + =
é = =é
Û Ûê ê = ±ê ë+ =ë
0,25
0,25
0,5
3 1 1 3 3
1 2 4 3
1 1
3 3
2012
x x dx
I dx I I
x x
-
= + = +ò ò
­Tính I1:
3 1 2
1 3
1
3
1
1
x I dx
x
-
= ò , đặt
3 2 2 3
2 2 3 3
1 1 2 3
1 1 3
2
dx dx
t t t dt t dt
x x x x
-
= - Þ = - Þ = Û = -
Đổi cận:
1
2; 1 0
3
x t x t= Þ = = Þ =
Khi đó
0
3 4
1
2
3 3
6
2 8
I t dt t= - = =ò
­Tính I2 = 8084
­Vậy I = 6 +8084 =8090
0,5
0,25
0,25
4
Gọi H là hình chiếu của S lên
(ABC); M, N, K lần lượt là
hình chiếu của H lênh cạnh
AB, AC, BC. Khi đó thể tích V
của khối chóp được tính bởi
công thức
1
.
3
ABC V S SHD=
mà
1
. 6
2
ABC S AB ACD = =
­Tính SH.
Xét các tam giác SHM, SHN,
0,25
0,25
B
A
H M
S
C N
K

4. SHK vuông tại H,
có các góc SMH, SNH, SKH
bằng 60 0
do đó HM = HN = HK => H là tâm đường tròn nội tiếp tam giác ABC =>
2
1 ABC S
HM
AB BC CA
= =
+ +
=>SH = HM.tan60 0
= 3
Vậy
1
3.6 2 3
3
V = =
0,25
0,25
5
2 2 2 2
2
2 2 3 1 0
4 2 2 0 x y x y
x xy x y
+ +
ì + - - + =ï
í
- - =ïî
<=>
2 2
2 2 2 2
2 2
2 2
2 2
2
(2 1)( 1) (2 1) 0
2 2 3 1 0
2 1
4 2 2 0
2 2
1
2 1 0
2
2 2 3
2 1 0
0 1
2 2
1 0
x y
x y x y
x y
x y
x y
x x y x
x xy x y
x x
y
x y
x x
y y
+
+ +
+
+
+
- - + - =ì
ïì + - - + =ï ïéÛ = -í íê- - =ï ïî ê =ïëî
éì
=é - =ì êïï ïê êí í
=êï êî ï = ±Û Ûê êïî+ - =ìê êï
íê = =êì ì
=ï Úêî í íë ê
= =î îë
Vậy hệ phương trình có 4 nghiệm là:...
0,5
0,25
0,25
6a.1 Giả sử D cắt d tại B => B(3 + t; 1 + 2t; 5 + 4t). Gọi H là hình chiếu của O lên D
khi đó O OH A£ do đó OH lớn nhất khi H trùng A,
như vậy đường thẳng D cần lập vuông góc với OA <=> . 0 AB OA =
uuur uuur
mà ( 1;2 2;4 4); (2;3;1) AB t t t OA= + - +
uuur uuur
,
nên . 0 AB OA =
uuur uuur
<=> 2t + 2 + 6t ­ 6 + 4t + 4 = 0 <=> t = 0 => B(3; 1; 5)
Vậy
3 1 5
:
1 2 4
x y z- - -
D = =
-
0,25
0,5
0,25
6a.2 M thuộc d1, N thuộc d2 nên M(2a ­ 1; a), N(b; 3b ­ 2)
2 2 2
5 5 ( 2 1) (3 2) 5 MN MN b a b a= Û = Û - + + - - = <=> (1)
3 3 / / . 0 ( 2 1;3 2).(2;1) 0 d MN d MN n b a b a a bÛ = Û - + - - = Û =
uuuur uur
thay vào (1) ta được a = b = 0 hoặc a = b = 2
Vậy có 4 điểm thoả mãn bài toán là: M(­1; 0), N(0; ­2) hoặc M(3; 2), N(2; 4)
0,25
0,5
0,25
7 ­Bộ 3 chữ số có tổng các chữ số bằng 7 gồm {0; 1; 6} (a), {0; 2; 5} (b), {0; 3; 4} (c),
{1; 2; 4} (d)
­Mỗi bộ trong các bô (a), (b), (c) có số cách lập là: 3! ­ 1.2.1 = 4 số (trừ chữ số 0
đứng đầu) => 3 trường hợp đầu có 12 số được lập
­Bộ (d) có 3! = 6 số được lập
­Vậy có 12 + 6 = 18 số được lập thoả mãn yêu cầu bài toán
0,25
0,25
0,25
0,25

5. 6b.1
­Đường tròn (C) có tâm
1 5
( ;2),
2 2
I R =
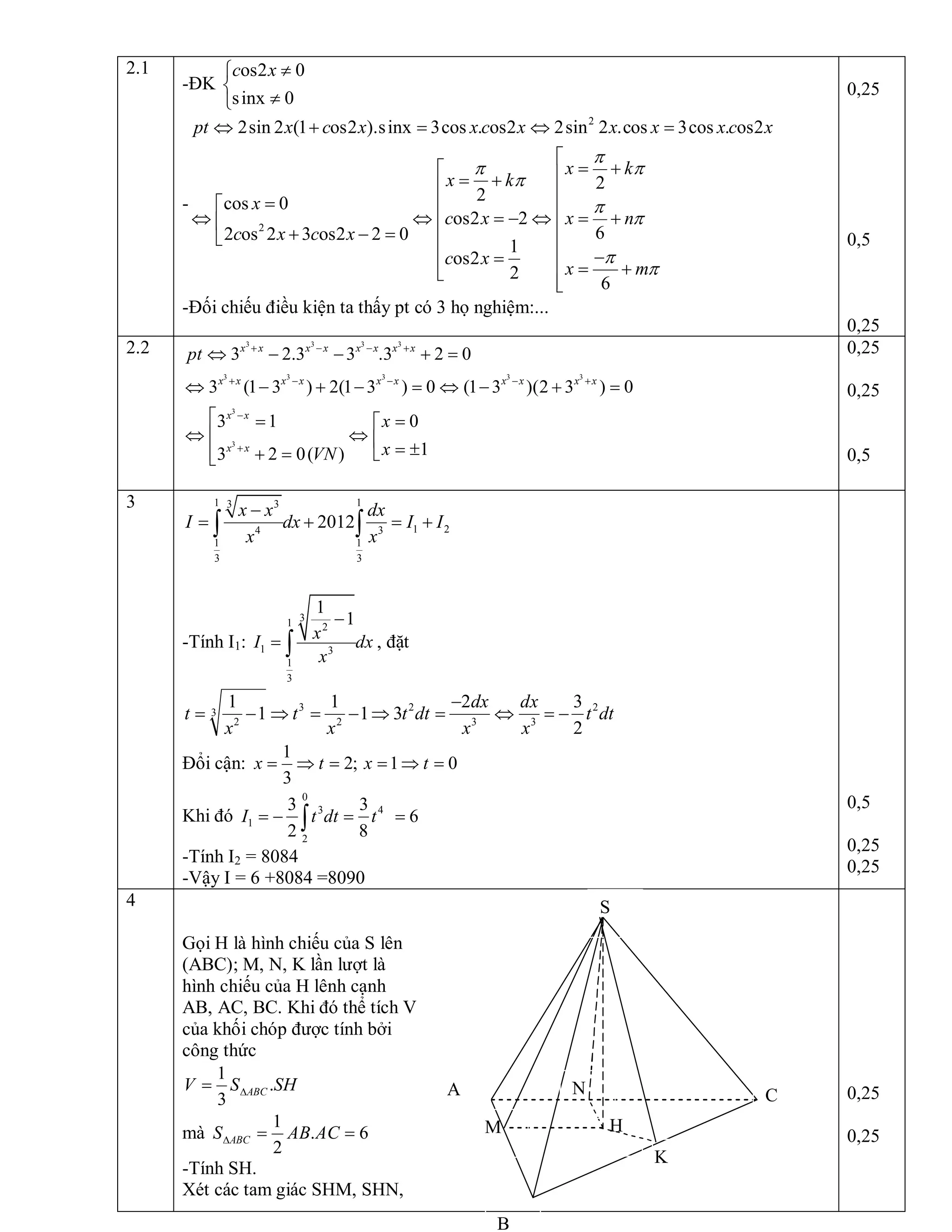
­Gọi H là trung điểm đoạn AB => H(5; ­4). Xét tam giác MAB có
2 2 2 2
2 2 2 2
2
2 4 2
MA MB AB AB
MH P MA MB MH
+
= - Û = + = +
do đó P nhỏ nhất khi MH nhỏ nhất hay M là giao điểm của OH với (C)
mà
5 3
:
4 4
x t
IH
y t
= +ì
í
= - -î
, thay vào phương trình đường tròn ta được ptrình t 2
+ 3t + 2 = 0
<=> t = ­1 và t = ­2 => với t = ­1 thì M(2; 0), với t = ­2 thì M(­1; 4)
­Kiểm tra thấy M(2; 0) là điểm cần tìm
0,25
0,25
0,25
0,25
6b.2 ­Giả sử B là giao điểm của d và D => B(1 + 3t; ­1 + t; 2t)
­Vì AB//(P) nên . 0 0 P AB n t= Û =
uuur uur
=> B(1; ­1; 0)
­Vậy đường thẳng D :
3 1 1
2 2 1
x y z- - -
= =
0,25
0,5
0,25
7b
2 x 0
2
2
2 2
x 0
2 2
1 cos2011x c 201x(1 cos2012x)
I lim
x
2011x
2sin
2sin 1006x c 2011x 2 .
x x 1 c 2012x
2011 8092265
) 2.(1006)
2 2
lim
®
®
- + -
=
= +
+
+ =
os
os
[ ]
os
=2.(
0,5
0,25
0,25