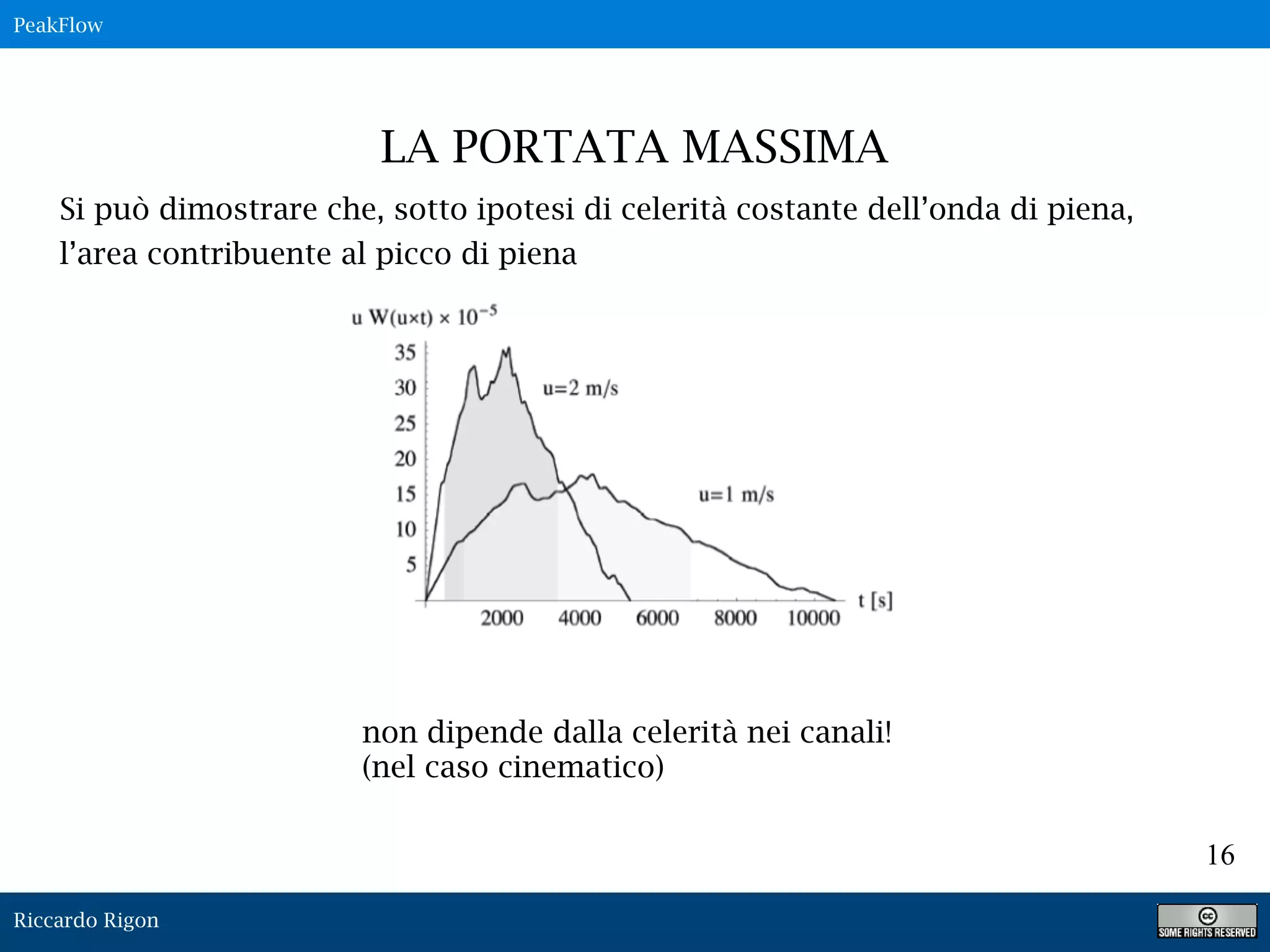
Il documento presenta la teoria dell'idrogramma istantaneo unitario per calcolare le portate massime e discute gli effetti geomorfologici associati. Vengono analizzati vari modelli di precipitazione e la loro influenza sulla portata di picco, evidenziando l'importanza degli intervalli di tempo di precipitazione. Si conclude con osservazioni sulla dipendenza della portata massima dalla durata della precipitazione e dall'area di bacino.

1. Riccardo Rigon
Le portate massime
ed effetti geomorfologici
Hokusai

2. Riccardo Rigon
2
Obiettivi
• Fatte alcune ipotesi semplificative
• Si usa la teoria dell’idrogramma istantaneo unitario per calcolare le
portate massime.
• Si discutono gli elementi teorici del modello Peakflow
Peakflow

3. Riccardo Rigon
3
0 50 100 150
0.00.20.40.60.81.0
Precipitazione [mm]
P[h]
1h
3h
6h
12h
24h
Tr = 10 anni
h1 h3 h6 h12 h24
LE PRECIPITAZIONI
sono assegnate attraverso le curve di possibilità pluviometrica

4. Riccardo Rigon
4
LE PRECIPITAZIONI
0.5 1.0 2.0 5.0 10.0 20.0
6080100120140160
Linee Segnalitrici di Possibilita' Pluviometrica
t [ore]
h[mm]
h(tp, Tr) = a(Tr) tn
p

5. Riccardo Rigon
5
LE PRECIPITAZIONI
0.5 1.0 2.0 5.0 10.0 20.0
6080100120140160
Linee Segnalitrici di Possibilita' Pluviometrica
t [ore]
h[mm]
h(tp, Tr) = a(Tr) tn
p
Altezza pluviometrica
coefficiente locale
esponente
durata “della
precipitazione”

6. Riccardo Rigon
6
LE PRECIPITAZIONI
0.5 1.0 2.0 5.0 10.0 20.0
6080100120140160
Linee Segnalitrici di Possibilita' Pluviometrica
t [ore]
h[mm]
Intensità della
precipitazione

7. Riccardo Rigon
7
Metodi per l’aggregazione del
deflusso superficiale - IUH
Nel nostro caso, avendo scelto di usare una
precipitazione di intensità costante come pioggia
di progetto e assunto che la pioggia efficace sia
proporzionale alla precipitazione, allora
Peakflow

8. Riccardo Rigon
8
H(x) =
0 x < 0
1 x 0
H(x) è nota come funzione di
Heaviside o funzione a gradino
Peakflow

9. Riccardo Rigon
9
Che cosa ci dice l’IUH sulla portata massima ?
Basta fare dQ/dt = 0 !
LA PORTATA MASSIMA
PeakFlow
d Q(t, tp)
dt
=
d
dt
Z t
0
IUH(t ⌧) H(t, tp)d⌧
H(t, tp) :=
⇢
1 0  t  tp
0 otherwise

10. Riccardo Rigon
10
Dopo un po’ di passaggi algebrici, la portata di picco
si ottiene risolvendo l’equazione:
LA PORTATA MASSIMA
PeakFlow
da cui deriva il tempo di picco t*
Henderson, 1963
IUH(t) = IUH(t tp)

11. Riccardo Rigon
11
LA PORTATA MASSIMA
PeakFlow
IUH(t)
IUH(t - tp)
IUH(t) =IUH(t - tp)
t*

12. Riccardo Rigon
12
Q(t; Tr, tp) = a(Tr) tn 1
p
t
t tp
IUH(t)dt
LA MASSIMA TRA LE MASSIME
PORTATE
Tuttavia, a ben osservare, la portata è anche una
funzione di tp. Per t > tp
Come conseguenza, la portata di picco, varia al variare
della durata della precipitazione (che vari con il tempo
di ritorno, è in un certo senso ovvio)
PeakFlow

13. Riccardo Rigon
13
Q(t; Tr, tp) = a(Tr) tn 1
p
t
t tp
IUH(t)dt
LA MASSIMA TRA LE MASSIME
PORTATE
Tuttavia, a ben osservare, la portata è anche una
funzione di tp. Per t > tp
L’intensità di precipitazione decresce all’aumentare di
tp, ma l’integrale aumenta. Per cui vi vi è un tempo
critico di precipitazione per cui si ottiene la massima tra
le portate di picco.
PeakFlow

14. Riccardo Rigon
14
La massima portata di picco si ottiene considerando il tempo di picco
come funzione della durata tp nell’equazione:
LA PORTATA MASSIMA- un po’ più
matematicamente
PeakFlow
t := t⇤
tp
Precipitazione
Variazione della precipitazione con la durata
Ritardo del tempo di picco
Area del bacino
S-Hydrograph al tempo t*

15. Riccardo Rigon
15
LA PORTATA MASSIMA- un po’ più
matematicamente
Se:
Allora:
E t* si ottiene da:
PeakFlow

16. Riccardo Rigon
16
Si può dimostrare che, sotto ipotesi di celerità costante dell’onda di piena,
l’area contribuente al picco di piena
non dipende dalla celerità nei canali!
(nel caso cinematico)
LA PORTATA MASSIMA
PeakFlow

17. Grazie per l’Attenzione

18. Riccardo Rigon
18

19. Riccardo Rigon
19

20. Riccardo Rigon
20
Credits and License
Questa presentazione è stata scritta da:
• Riccardo Rigon (Università di Trento)
La citazione corretta è: Rigon, The modern theory of IUH Real Books of Hydrology,
Dipartimento di Ingegneria Civile ed Ambientale, Università di Trento, 2012.
p-peakflowTheory è rilasciato con licenza Creative Commons Attribution-ShareAlike
3.0 Unported License. Tale licenza si può trovare al sito http://creativecommons.org/
licenses/by-sa/3.0/deed.it