Il documento presenta una discussione sull'uso delle distribuzioni di valori estremi, in particolare la distribuzione di Gumbel, Frechet e Weibull, per modellare le precipitazioni estreme. Viene spiegato un teorema che collega le distribuzioni di massimi selezionati a famiglie di distribuzioni specifiche. Infine, si introduce la distribuzione generalizzata dei valori estremi (GEV), evidenziando la sua importanza e applicabilità in questo contesto.

1. Le precipitazioni estreme -
GEV
Riccardo Rigon
Michelangelo,Ildiluvio,1508-1509

2. R. Rigon
Obbiettivi:
!2
•Generalizzare i concetti esposti in precedenza sulle precipitazioni
estreme
Introduzione

3. R. Rigon
A little more formal
L’uso della distribuzione di Gumbel non deriva da un capriccio ma da un
Teorema, il quale afferma che, sotto ipotesi abbastanza generali, la
distribuzione dei massimi scelti da campioni di opportuna numerosità
non può che appartenere ad una delle seguenti famiglie di distribuzioni:
I) Distribuzione di Gumbel
G(z) = e e
z b
a
⇥ < z < ⇥
a > 0
!3
Distribuzioni dei valori estremi

4. R. Rigon
L’uso della distribuzione di Gumbel non deriva da un capriccio ma da un
Teorema, il quale afferma che, sotto ipotesi abbastanza generali, la
distribuzione dei massimi scelti da campioni di opportuna numerosità non
può che appartenere ad una delle seguenti famiglie di distribuzioni:
II) Distribuzione di Frechèt
G(z) =
0 z b
e (z b
a ) z > b
> 0a > 0
A little more formal
!4
Distribuzioni dei valori estremi

5. R. Rigon
Media
Moda
Mediana
Varianza
P[X < x] = e x
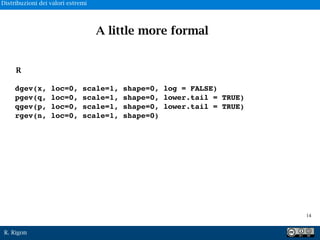
A little more formal
II) Distribuzione di Frechèt
from Wikipedia
!5
Distribuzioni dei valori estremi

6. R. Rigon
dfrechet(x, loc=0, scale=1, shape=1, log = FALSE)
pfrechet(q, loc=0, scale=1, shape=1, lower.tail = TRUE)
qfrechet(p, loc=0, scale=1, shape=1, lower.tail = TRUE)
rfrechet(n, loc=0, scale=1, shape=1)
R:
A little more formal
!6
Distribuzioni dei valori estremi

7. R. Rigon
L’uso della distribuzione di Gumbel non deriva da un capriccio ma da un
Teorema, il quale afferma che, sotto ipotesi abbastanza generali, la
distribuzione dei massimi scelti da campioni di opportuna numerosità non
può che appartenere ad una delle seguenti famiglie di distribuzioni:
> 0
a > 0
G(z) = e [ (z b
a )] z < b
1 z b
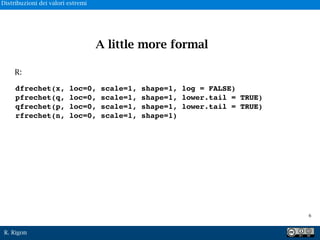
A little more formal
III) Distribuzione di Weibull
!7
Distribuzioni dei valori estremi

8. R. Rigon
from Wikipedia
III) Distribuzione di Weibull
(P. Rosin and E. Rammler, 1933)
A little more formal
!8
Distribuzioni dei valori estremi

9. R. Rigon
Quando k = 1, la distribuzione di Weibull
si riduce alla distribuzione esponenziale.
Quando k = 3.4, la distribuzione Weibull
diventa molto simile alla distribuzione
normale.
Media
Moda
Mediana
Varianza
from Wikipedia
III) Distribuzione di Weibull
(P. Rosin and E. Rammler, 1933)
A little more formal
!9
Distribuzioni dei valori estremi

10. R. Rigon
dweibull(x, shape, scale = 1, log = FALSE)
pweibull(q, shape, scale = 1, lower.tail = TRUE, log.p = FALSE)
qweibull(p, shape, scale = 1, lower.tail = TRUE, log.p = FALSE)
rweibull(n, shape, scale = 1)
R:
A little more formal
!10
Distribuzioni dei valori estremi

11. R. Rigon
Il teorema suddetti tuttavia può essere riformulato in funzione di una
distribuzione a tre parametri detta Generalized Extreme Values o GEV
G(z) = e [1+ (z µ
⇤ )] 1/⇥
z : 1 + ⇥(z µ)/⇤ > 0
⇥ < µ < ⇥ ⇤ > 0
⇥ < ⇥ < ⇥
Per la distribuzione degenera nella distribuzione di Gumbel
Per la distribuzione diviene una distribuzione di Frechèt
Per la distribuzione diviene una Weibull
= 0
> 0
< 0
A little more formal
!11
Distribuzioni dei valori estremi

12. R. Rigon
Il teorema suddetti tuttavia può essere riformulato in funzione di una
distribuzione a tre parametri detta Generalized Extreme Values o GEV
G(z) = e [1+ (z µ
⇤ )] 1/⇥
z : 1 + ⇥(z µ)/⇤ > 0
⇥ < µ < ⇥ ⇤ > 0
⇥ < ⇥ < ⇥
A little more formal
!12
Distribuzioni dei valori estremi

13. R. Rigon
gk = (1 k )
Il teorema suddetti tuttavia può essere riformulato in funzione di una
distribuzione a tre parametri detta Generalized Extreme Values o GEV
A little more formal
!13
Distribuzioni dei valori estremi

14. R. Rigon
dgev(x, loc=0, scale=1, shape=0, log = FALSE)
pgev(q, loc=0, scale=1, shape=0, lower.tail = TRUE)
qgev(p, loc=0, scale=1, shape=0, lower.tail = TRUE)
rgev(n, loc=0, scale=1, shape=0)
R
A little more formal
!14
Distribuzioni dei valori estremi

15. R. Rigon
Grazie per l’attenzione!
G.Ulrici,2000?
15