Il documento descrive il test di Pearson come un metodo non parametrico per analizzare le precipitazioni estreme, suddividendo il campo di probabilità in parti e contando i dati in ciascun intervallo. Il processo include la valutazione delle funzioni p[h < h0] e la scelta dei parametri per trovare il valore di x2 più piccolo. Infine, il test viene ripetuto per differenti durate di precipitazione per ottenere linee segnalitrici di possibilità pluviometrica.

1. Le precipitazioni estreme
Gumbel-Test di Pearson
Riccardo Rigon
Kandinski-CompositionVI(Ildiluvio)-1913

2. R. Rigon
Il test di Pearson è un test NON parametrico e consiste:
1 - Nel suddividere il campo di probabilità in k parti, per esempio uguali
!2
Il Test di Pearson
Stima dei parametri

3. R. Rigon
Il test di Pearson è un test NON parametrico e consiste:
2 - derivarne una suddivisione del dominio
!3
Il Test di Pearson
Test delle ipotesi

4. R. Rigon
Il test di Pearson è un test NON parametrico e consiste:
3 - Contare il numero di dati in ciascun intervallo (tra i cinque della figura)
!4
Il Test di Pearson
Test delle ipotesi

5. R. Rigon
Il test di Pearson è un test NON parametrico e consiste:
3 - Contare il numero di dati in ciascun intervallo (tra i cinque della figura)
!5
Il Test di Pearson
7
7
9
13
7
Test delle ipotesi

6. R. Rigon
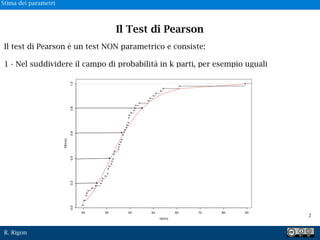
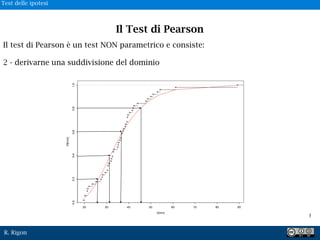
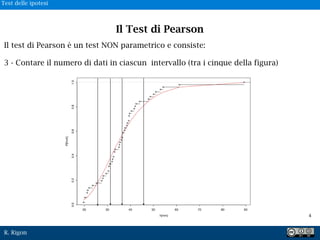
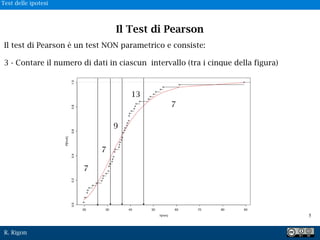
Il test di Pearson è un test NON parametrico e consiste:
6 - Valutare la funzione
P[H < h0] = P[H < 0]
P[H < hn+1] = P[H < ]
dove:
!6
Il Test di Pearson
Test delle ipotesi

7. R. Rigon
Il Test di Pearson
Quindi:
e nel caso della figura delle slides precedenti
(P[H < hj+1] P[H < hj]) = 0.2
7
Test delle ipotesi

8. R. Rigon
Il Test di Pearson
6 - Scegliere la coppia di parametri per cui X2 è più piccolo
7 - Si ripetono tutte le operazioni per ogni durata (ad esempio, 1, 3, 6, 12, 24
ore): visto che tutte le procedure si riferiscono ad una singola durata
Per completare il tutto
8
Test delle ipotesi

9. R. Rigon
0 50 100 150
0.00.20.40.60.81.0
Precipitazione [mm]
P[h]
1h
3h
6h
12h
24h
!9
Dopo aver applicato Pearson
e ripetuto l’operazione per ognii durata
Le linee segnalitrici di possibilità pluviometrica