Download as PDF, PPTX
Uploaded byRiccardo Rigon
Peakflow
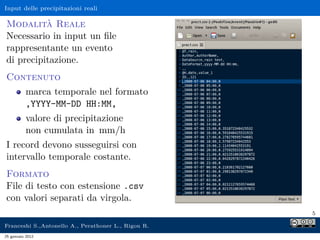
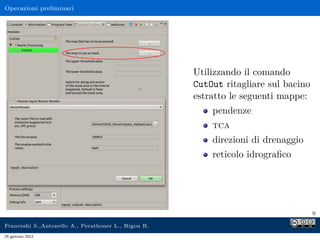
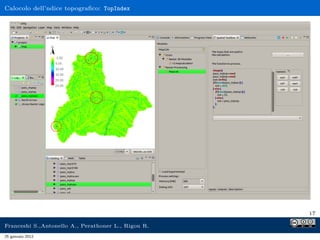
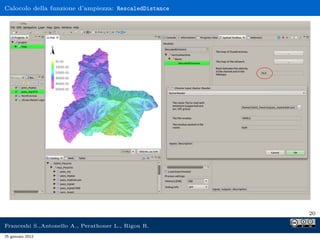
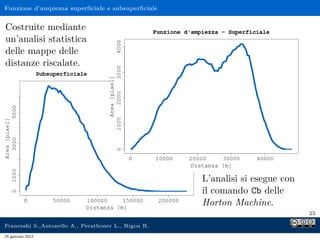
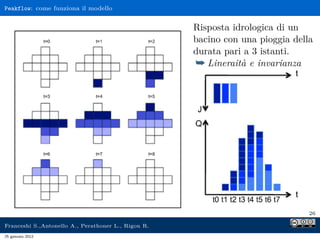
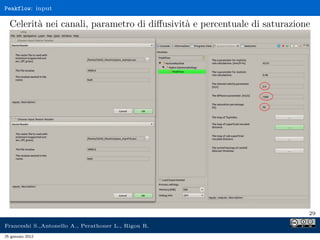
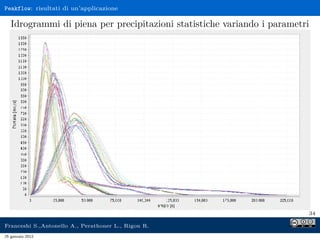
Il documento presenta l'analisi idrologica tramite il modello PeakFlow, un modello afflussi-deflussi semidistribuito che utilizza l'approccio dell'idrogramma istantaneo unitario geomorfologico. Vengono descritte le modalità di funzionamento, le operazioni preliminari necessarie e i parametri richiesti per l'analisi. Inoltre, si approfondisce il comportamento dunniano del modello, evidenziando le differenze tra deflusso superficiale e subsuperficiale.
Peakflow
- 1. Analisi idrologica conPeakflow Silvia Franceschi, Andrea Antonello, Leonardo Perathoner e Riccardo Rigon 25 gennaio 2012
- 2. Credits Questa presentazione èstata scritta da: Silvia Franceschi (Hydrologis and Ispra) Andrea Antonello (Hydrologis) Leonardo Perathoner (Università di Trento) Riccardo Rigon (Università di Trento) La redazione di questa presentazione è stata supportata da Ispra nell’ambito del progetto Danube Flood Risk e dalla Provincia Autonoma di Bolzano, nell’ambito del progetto HydroAlp. Per quanto possibile, questa presentazione è stata redatta con l’uso di software libero. LATEXper a scrittura, per il quale Leonardo Perathoner ha approntato un apposito stile. Il programma statistico R (http://cran.r-project.org/) per l’elaborazione delle figure non prodotte da uDig. 1 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 3. “Free Software .. . you should think of ‘free’ as in ‘free speech’, not as in ‘free beer’. ” Richard Stallman 2 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 4. Descrizione del modello Peakflowè un modello idrologico afflussi-deflusssi semidistribuito integrato nei JGrass tools. utilizza l’approccio dell’Idrogramma Istantaneo Unitario Geomorfologicao -GIUH- applica il GIUH utilizzando il modello della funzione d’ampiezza lavora a scala d’evento è stato pensato per il calcolo delle precipitazioni massime 3 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 5. Descrizione del modello Lavorain due modalità: statistica utilizza le precipitazioni massime per un dato tempo di ritorno dati i parametri a ed n considera la pioggia costante nell’intervallo di simulazione calcola la durata di pioggia che massimizza la portata alla chiusura calcola la portata massima per l’evento considerato 4 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 6. Descrizione del modello Lavorain due modalità: statistica utilizza le precipitazioni massime per un dato tempo di ritorno dati i parametri a ed n considera la pioggia costante nell’intervallo di simulazione calcola la durata di pioggia che massimizza la portata alla chiusura calcola la portata massima per l’evento considerato reale utilizza un evento di precipitazione reale fornito in input p(t) −→ IUH −→ Q(t) suppone la distribuzione degli ietogrammi rettangolare modella l’idrogramma alla chiusura del bacino 4 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 7. Input delle precipitazionireali Modalità Reale Necessario in input un file rappresentante un evento di precipitazione. Contenuto marca temporale nel formato ,YYYY-MM-DD HH:MM, valore di precipitazione non cumulata in mm/h I record devono susseguirsi con intervallo temporale costante. Formato File di testo con estensione .csv con valori separati da virgola. 5 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 8. Parametri necessari Analisi pluviometrica Parametripluviometrici a e n oppure Misurazioni di precipitazioni in mm/h Analisi idraulica Velocità nei canali Parametro di diffusione Analisi geomorfologica Percentuale satura di bacino Funzione d’ampiezza Rapporto tra velocità nei canali e nei versanti 6 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 9. Operazioni preliminari depittare ilfile delle elevazioni definire le direzioni di drenaggio per ogni punto disegnare la rete di drenaggio stabilire la sezione di chiusura alla quale verrà calcolata la portata estrarre i limiti del bacino con tale chiusura 7 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 10. Operazioni preliminari dtm Pitfiller Slope DrainDir Tca ExtractNetwork Subsuperficial RescaledDistance Superficial RescaledDistance TopIndex Analisidelle precipitazioni a & n oppure Hyetograph Peakflow - - ? ? ? ? ? ? ? ? ? ? 8 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 11. Operazioni preliminari Utilizzando ilcomando CutOut ritagliare sul bacino estratto le seguenti mappe: pendenze tca direzioni di drenaggio reticolo idrografico 9 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 12. Operazioni preliminari La sceltadi ritagliare le mappe sulla maschera del bacino estratto non è casuale. Le opzioni di lavoro sarebbero due: rifare i calcoli delle grandezze principali sul DTM del bacino estratto ritagliare le mappe sulla maschera del bacino 10 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 13. Operazioni preliminari La sceltadi ritagliare le mappe sulla maschera del bacino estratto non è casuale. Le opzioni di lavoro sarebbero due: rifare i calcoli delle grandezze principali sul DTM del bacino estratto ritagliare le mappe sulla maschera del bacino La prima opzione prevede di ricalcolare la mappa delle elevazioni depittata e le direzioni di drenaggio. Questo può comportare incompatibilità con il dato di partenza. 10 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 14. Area satura delbacino 1 Definizione della percentuale di saturazione del bacino la percentuale di saturazione del bacino in occasione di un evento di piena è generalmente il 40 − 60% la percentuale di saturazione aumenta al diminuire delle dimensioni del bacino il massimo di saturazione si ha nelle zone concave del bacino sarebbero utili misure di portata o di umidità del suolo per tarare il modello 11 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 15. Area satura delbacino 1 Definizione della percentuale di saturazione del bacino la percentuale di saturazione del bacino in occasione di un evento di piena è generalmente il 40 − 60% la percentuale di saturazione aumenta al diminuire delle dimensioni del bacino il massimo di saturazione si ha nelle zone concave del bacino sarebbero utili misure di portata o di umidità del suolo per tarare il modello 2 Si utilizza l’indice topografico per identificare le zone sature zone sature in prossimità della rete ¯ meccanismo di saturazione dunniano 11 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 16. Indice topografico esprime latendenza di un pixel a saturarsi ¯ aree con valori elevati di indice topografico si saturano prima di aree a basso indice topografico dipende solo dalla morfologia discrimina i siti che danno deflusso superficiale da quelli che danno solo contributo subsuperficiale è proporzionale al rapporto tra area cumulata nel pixel e pendenza 12 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 17. Calcolo dell’ndice topografico:TopIndex input 13 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 18. Calcolo dell’ndice topografico:TopIndex output 14 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 19. Calocolo dell’ndice topografico:TopIndex Pixel con pendenza bassa hanno elevata propensione alla saturazione a parità di area cumulata ci sono zone all’interno del bacino dove non è definito l’indice topografico ¯ sono quelle con pendenza pari a zero per cui il rapporto area cumulata su pendenza tende ad infinito Si assegna ai pixel con valore nullo di indice topografico il valore massimo caratteristico della mappa utilizzando MapCalc: images{ pass_mytop=read; pass_mybas=read; out=write;} if (isnan( pass_mybas )) { out = null; } else { if (isnan( pass_mytop )) { out = 25; } else { out = pass_mytop; } ; }; 15 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 20. Calocolo dell’ndice topografico:TopIndex 16 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 21. Calocolo dell’ndice topografico:TopIndex 17 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 22. Funzione d’ampiezza Utilizzando ilcriterio della massima pendenza ogni punto del bacino è collocato ad una nota distanza dalla sezione di chiusura. La funzione d’ampiezza rappresenta la distribuzione di tali distanze. Numericamente è costituita dal numero di pixel posti a distanza uguale dalla sezione di chiusura (misurata lungo le direzioni di drenaggio a partire dalla sezione di chiusura). W (x) = 1 AT µ{a | d(a) = x} 18 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 23. Funzione d’ampiezza Utilizzando ilcriterio della massima pendenza ogni punto del bacino è collocato ad una nota distanza dalla sezione di chiusura. La funzione d’ampiezza rappresenta la distribuzione di tali distanze. Numericamente è costituita dal numero di pixel posti a distanza uguale dalla sezione di chiusura (misurata lungo le direzioni di drenaggio a partire dalla sezione di chiusura). W (x) = 1 AT µ{a | d(a) = x} La funzione d’ampiezza riscalata tiene conto della diversa velocità dell’acqua nella rete e nei versanti introducendo r come rapporto tra la velocità nei canali e nei versanti. TR = Tc + Th = xc uc + xh uh = 1 uc xc + uc uh xh = x uc x = xc + r · xh con r = uc uh =⇒ W (x ) 18 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 24. Calocolo della funzioned’ampiezza: RescaledDistance 1 Per calcolare una mappa che contenga le informazioni della funzione d’ampiezza riscalata si utilizza il comando RescaledDistance. Tale comando calcola la distanza dalla sezione di chiusura considerando velocità diverse nei versanti e nella rete. 19 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 25. Calocolo della funzioned’ampiezza: RescaledDistance 1 Per calcolare una mappa che contenga le informazioni della funzione d’ampiezza riscalata si utilizza il comando RescaledDistance. Tale comando calcola la distanza dalla sezione di chiusura considerando velocità diverse nei versanti e nella rete. 2 Per applicare tale comando, se abbiamo ritagliato le mappe sul bacino estratto, è necessario usare il comando MarkoOtlet. Questo serve per segnare l’uscita e velocizzare tutti gli algoritmi che si riferiscono ad essa. 19 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 26. Calocolo della funzioned’ampiezza: RescaledDistance 20 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 27. Calocolo della funzioned’ampiezza: RescaledDistance 21 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 28. Funzione d’ampiezza inPeakflow In Peakflow vengono considerati separatamente il deflusso superficiale e subsuperficiale. Si lavora nell’ipotesi di comportamento dunniano ¯ saturazione dal basso o per eccesso di saturazione quindi il deflusso superficiale si ha dove il suolo è già saturo. La porzione di bacino satura è in equilibrio tra deflusso superficiale e subsuperficiale, la porzione non satura del bacino concorre solo alla formazione del deflusso subsuperficiale. 22 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 29. Schema di funzionamento Subsuperficial RescaledDistance Superficial RescaledDistance TopIndexHyetograph ? Peakflow SubsuperficialRescaledDistance Superficial RescaledDistance Subsuperficial WidthFunction Superficial WidthFunction Top Index Area non satura Area satura Hyetograph Q Subsuperficial Q Superficial ? ? ? ? - - - Hydrograph ? 23 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 30. Funzione d’ampiezza: zonesature e zone non sature Funzione d’ampiezza superficiale Riguarda solamente le zone sature del bacino Si utilizzano mappe delle distanze riscalate con valori di r bassi {5 − 20} ¯ Si fornisce in input a Peakflow la mappa delle distanze riscalate superficiali sull’intero bacino 24 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 31. Funzione d’ampiezza: zonesature e zone non sature Funzione d’ampiezza superficiale Riguarda solamente le zone sature del bacino Si utilizzano mappe delle distanze riscalate con valori di r bassi {5 − 20} ¯ Si fornisce in input a Peakflow la mappa delle distanze riscalate superficiali sull’intero bacino Funzione d’ampiezza subsuperficiale Riguarda solamente le zone non sature del bacino Si utilizzano mappe delle distanze riscalate con valori di r alti {50 − 200} ¯ Si fornisce in input a Peakflow la mappa delle distanze riscalate subsuperficiali sull’intero bacino 24 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 32. Funzione d’ampiezza superficialee subsuperficiale Costruite mediante un’analisi statistica delle mappe delle distanze riscalate. L’analisi si esegue con il comando Cb delle Horton Machine. 25 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 33. Peakflow: come funzionail modello Risposta idrologica di un bacino con una pioggia della durata pari a 3 istanti. ¯ Lineraità e invarianza 26 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 34. Peakflow: teoria delmodello Intensità di precipitazione costante p(τ, tp) = p · H(τ)H(tp − τ) Idrogramma Istantaneo Unitario Q(t) = AT × t 0 IUH(t − τ) · p(τ) dτ Tempo di picco IUH(t∗) = IUH(t∗ − tp) Portate istantanee Q(t) = AT · p A(t) se 0 ≤ t ≤ tp AT · p A(t) − A(t − tp) se t tp 27 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 35. Peakflow: teoria delmodello Intensità di precipitazione costante p(τ, tp) = p · H(τ)H(tp − τ) Idrogramma Istantaneo Unitario Q(t) = AT × t 0 IUH(t − τ) · p(τ) dτ Tempo di picco IUH(t∗) = IUH(t∗ − tp) Portate istantanee Q(t) = AT · p A(t) se 0 ≤ t ≤ tp AT · p A(t) − A(t − tp) se t tp Portata di picco Qp(t∗) = AT · p A(t∗) − A(t∗ − tp) se 0 ≤ tp ≤ τc AT · p A(t∗ = τc) = AT · p se tp τc Curve di possibilità pluviometrica p(tp) = a(TR) · t−m p Tempo di precipitazione critico m = AT tp· IUH(t∗) A(t∗)−A(t∗−tp) ≡ g(tp) 27 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 36. Peakflow: input Mappe dell’indicetopografico e delle distanze riscalate superficiali e sub 28 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 37. Peakflow: input Celerità neicanali, parametro di diffusività e percentuale di saturazione 29 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 38. Peakflow: statistical raininput Coefficienti delle curve di possibilità pluviometrica 30 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 39. Peakflow: real raininput Lettura del file di precipitazioni di un evento reale 31 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 40. Peakflow: discharge output Scritturadel file di output della simulazione 32 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 41. Peakflow: risultati diun’applicazione Modalità Statistica Finita l’elaborazione restituisce: il tempo di precipitazione critico la portata di picco 33 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 42. Peakflow: risultati diun’applicazione Modalità Statistica Finita l’elaborazione restituisce: il tempo di precipitazione critico la portata di picco Inoltre scrive il file delle portate ad ogni secondo per poter plottare l’idrogramma di piena. 33 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 43. Peakflow: risultati diun’applicazione Idrogrammi di piena per precipitazioni statistiche variando i parametri 34 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 44. Peakflow: risultati diun’applicazione Modalità Reale Finita l’elaborazione scrive il file .csv contenente le portate alla chiusura modellate ogni secondo. le portate sono espresse in m3/s ad ogni valore è associata la rispettiva marca temporale grazie a questo file e possibile plottare con un software esterno l’idrogramma modellato per l’evento analizzato. 35 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 45. Peakflow: risultati diun’applicazione Idrogramma simulato per un evento reale 36 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012
- 46. Grazie dell’attenzione Riferimenti bibliografici Rigon,R., P. D’Odorico e G. Bertoldi (2011). “The geomorphic structure of the runoff peak”. In: Hydrology and Earth System Sciences 15.6, pp. 1853–1863. url: http://www.hydrol-earth-syst-sci.net/15/1853/2011/. 37 Franceshi S.,Antonello A., Perathoner L., Rigon R. 25 gennaio 2012