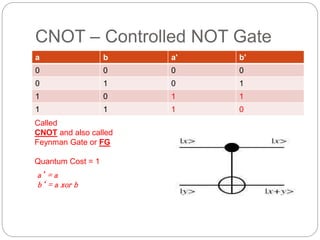
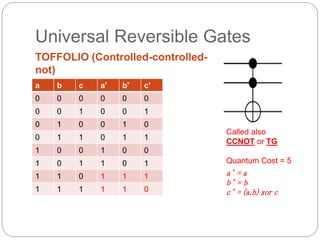
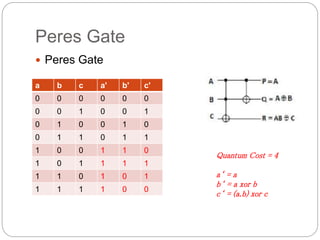
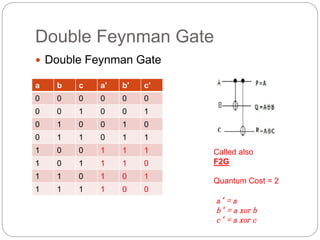
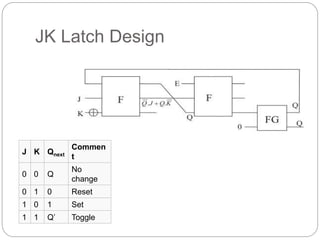
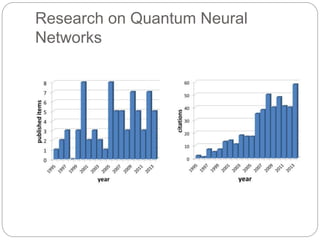
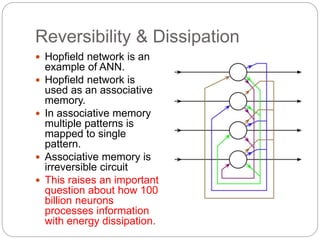
The document provides an in-depth overview of quantum computing, including key concepts like qubits, quantum superposition, and entanglement, and their implications for information processing. It discusses quantum gates, reversible logic, and the potential for quantum neural networks. Additionally, it references various academic contributions and research on the intersection of quantum mechanics and computational theory.

1. Amr Kamel Ahmed
PHD Preparatory - 2014
Helwan University – Computer
Engineering
Quantum Computing & Quantum
Information

2. Introduction

3. Definitions
 A quantum computer is a computation system
that makes direct use of quantum-mechanical
phenomena (such as superposition and
entanglement), to perform operations on data.[1]
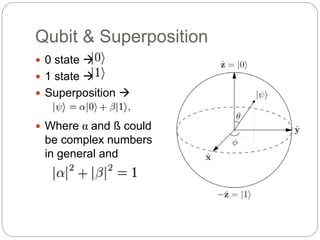
 Quantum superposition is a fundamental
principle of quantum mechanics that holds a
physical system — such as an electron — exists
partly in all its particular theoretically possible
states simultaneously; but when measured or
observed, it gives a result corresponding to
only one of the possible configurations

4. Definitions - Qubit
 In quantum computing, a qubit or quantum bit is a
unit of quantum information — the quantum
analogue of the classical bit. A qubit is a two-
state quantum-mechanical system
 Such as the polarization of a single photon: here the
two states are vertical polarization and horizontal
polarization.
 In a classical system, a bit would have to be in one
state or the other, but quantum mechanics allows
the qubit to be in a superposition of both states
at the same time, a property which is fundamental
to quantum computing.

5. Qubit & Superposition
 0 state 
 1 state 
 Superposition 
 Where α and ß could
be complex numbers
in general and

6. Classical Bits

7. Qubits
Opening the same door reads the same
•Opening the complementary
door gives completely random
result.
•Opening the wrong door
destroys information.
•No quantum copying machine
for unknown state qubit

8. Multiple Qubit Superposition
 The number of superpositions of n qubits are 2^n
superpositions
 So the number of superpositions of 300 qubits are
2^300 which is greater than the number of atoms of
the appearing universe
 It is really a huge number; however; the number of
possible information also are much higher.
 Note that the number of possible distinct Boolean
circuits for n inputs and one output are 2^(2^n)
 when n=8  number of circuits = 2^256
 when n=16  number of circuits = 2^65536

9. Quantum Entanglement
 Quantum entanglement is a physical
phenomenon that occurs when pairs or groups of
particles are generated or interact in ways such
that the quantum state of each particle cannot
be described independently—instead, a
quantum state may be given for the system as
a whole.
 It thus appears that one particle of an entangled
pair "knows" what measurement has been
performed on the other, and with what outcome,
even though there is no known means for such
information to be communicated between the
particles, which at the time of measurement may be
separated by arbitrarily large distances.

10. Entangled Qubits
 Although the measurement of the value of each
single qubit is completely random.
 When they two qubits are entangled a correlation
is established between the two bits such that the
value of one qubit could be the same or the
opposite value of the other.
 However; this correlated information couldn’t be
measured locally on single qubit. It should be
collectively measured (globally measured).

11. Entangled Qubits
 Erwin Schrodinger:- “The best possible
knowledge of a whole does not necessarily
include the best knowledge of all its parts, even
though they may be entirely separated and
therefore virtually capable of being ‘best possibly
known’”
 John Preskill:- “The whole is definite, the part is
random”

12. Why Entanglement is important
 Each satellite will generate a constant stream of
entangled pairs.
 Each member of the pair will be sent to separate
stations on the ground, where it will be stored in
quantum memories.
 Once the entanglement is stored on the ground, it can
then be used as needed to send secure messages, or
even sent locally across the quantum Internet using

13. Quantum Logic

14. Cost of Information Loss
 Fundamental logic dictates that energy must be
dissipated when information is erased
 Energy dissppated = kT . Ln2 per bit erased
 k:- Boltzman constant (1.3805*10-23 JK-1)
 T :- Absolute temprature (in degrees Kelvin)
 One way of suppressing this unwanted heat is by
modifying the chip design to use only reversible
logic gates

15. Reversible Gates
 In reversible gates there is always a unique input
associated with a unique output and vise versa.
 So reversible logic never erase any information
when they act

16. Unitary Gates
 Hadamard equation  Makes superposition
 |0> 
 |1> 
 Pauli-X gate
 |0>  |1>
 |1>  |0>
 Pauli-Y gate
 |0>  i |1>
 |1>  -i |0>
 Pauli-Z gate (Phase shift gate with )
 |0>  unchanged
 |1>  - |1>

17. Not & Swap gates
Not Gate Swap Gate
a a’
0 1
1 0
a b a' b'
0 0 0 0
0 1 1 0
1 0 0 1
1 1 1 1

18. CNOT – Controlled NOT Gate
a b a' b'
0 0 0 0
0 1 0 1
1 0 1 1
1 1 1 0
Called
CNOT and also called
Feynman Gate or FG
Quantum Cost = 1
a’ = a
b‘ = a xor b

19. Universal Reversible Gates
TOFFOLIO (Controlled-controlled-
not)
a b c a' b' c'
0 0 0 0 0 0
0 0 1 0 0 1
0 1 0 0 1 0
0 1 1 0 1 1
1 0 0 1 0 0
1 0 1 1 0 1
1 1 0 1 1 1
1 1 1 1 1 0
Called also
CCNOT or TG
Quantum Cost = 5
a‘ = a
b‘ = b
c‘ = (a.b) xor c

20. Peres Gate
 Peres Gate
a b c a' b' c'
0 0 0 0 0 0
0 0 1 0 0 1
0 1 0 0 1 0
0 1 1 0 1 1
1 0 0 1 1 0
1 0 1 1 1 1
1 1 0 1 0 1
1 1 1 1 0 0
Quantum Cost = 4
a‘ = a
b‘ = a xor b
c‘ = (a.b) xor c

21. Double Feynman Gate
 Double Feynman Gate
a b c a' b' c'
0 0 0 0 0 0
0 0 1 0 0 1
0 1 0 0 1 0
0 1 1 0 1 1
1 0 0 1 1 1
1 0 1 1 1 0
1 1 0 1 0 1
1 1 1 1 0 0
a‘ = a
b‘ = a xor b
c‘ = a xor c
Called also
F2G
Quantum Cost = 2

22. Universal Reversible Gates
FREDKIN (Controlled-Swap)
a b c a' b' c'
0 0 0 0 0 0
0 0 1 0 0 1
0 1 0 0 1 0
0 1 1 0 1 1
1 0 0 1 0 0
1 0 1 1 1 0
1 1 0 1 0 1
1 1 1 1 1 1
Also called F gate
Quantum Cost = 5
a‘ = a
b‘ = not(a).b + a.c
c‘ = a.b + not(a).c

23. Quantum Circuits

24. SR Latch Circuit
Conventional Cross
Coupled Design – NAND
SR Latch
Pres Gates based
design without Enable
S R Action
0 0
not
allowed
0 1 Q = 1
1 0 Q = 0
1 1
No

25. SR Latch Circuit
Other design of
SR Latch
This design is
gated design
including
“Enable” input

26. Gated D Latch
E/C D Q Q
Comme
nt
0 X
Qpre
v
Qpre
v
No
change
1 0 0 1 Reset
1 1 1 0 Set

27. JK Latch Design
J K Qnext
Commen
t
0 0 Q
No
change
0 1 0 Reset
1 0 1 Set
1 1 Q’ Toggle

28. Quantum Neural Networks
(QNN)

29. Research on Quantum Neural
Networks

30. Reversibility & Dissipation
 Hopfield network is an
example of ANN.
 Hopfield network is
used as an associative
memory.
 In associative memory
multiple patterns is
mapped to single
pattern.
 Associative memory is
irreversible circuit
 This raises an important
question about how 100
billion neurons
processes information
with energy dissipation.

31. Non Linear Activation
 Non-Linear activation
functions is an
important characteristic
of neural networks.
 It is a source for non-
linear properties of
neural networks
 Sigmoid function is the
most famous example
 One open issue of
Quantum Neural
Networks is how to
incorporate non-linear
functions in quantum
systems which is linear

32. Qubit Neurons (Qurons)
 A quron is a qubit in
which the two levels
stand for active an
resting neural firing
states.
 This allows for neural
network to be in a
superposition of firing
patterns.

33. Ideas for Interpreting Step Function
as Measurement
 KAK intoduced the idea of
quantum neural computation
 In a Hopfield like network he
interpreted the necessary
conditions for a stable states
as an eigen value equation
of a quantum system
 Updating a network
corresponds to quantum
measurement selects the
eigenstates of the system
 Meneer & Narayanan the
many-universe interpretation
of quantum mechanics to
look at superposition of
networks each storing one
pattern instead-of one
network storing several
patterns
 ZAK & Willimas do not
consider single neurons as
quantum objects but
introduce a unitary walk
between quantum network
basis states.
 This approaches using
nonlinear dissipative and
irreiversible transformation
as a trial for playing the role
of a natural quantum sigmoid
function

34. Interacting Quantum Dots
 The green function by
Feynman sums all
possible paths prpagating
the system
 Elizabeth Behrman
noticed the nonlinearity of
the equation.
 Instead of different
Qurons the network is
realized by propagation of
one Quron only
 Its state after each of N
different time slices
simulates the states of N
virtual neurons.
 Synaptic weights are
engineered by interaction
of the Quron with the
environment
 Behraman proposes to
implement this “time-array
neural network” as
quantum dot molecule
interacting with phonons
of surrounding lattice &
external field
 The network can be
trained by back-
propagation rule

35. References
1. "Quantum Computing with Molecules" article in
Scientific American by Neil Gershenfeld and Isaac
L. Chuang, 1998
2. “Quantum Computation and Quantum Information”
book by Micheal A.Nilesen & Isaac L. Chuang,
Cambridge University Press, 2000
3. “Quantum Computing & the Entanglement Frontier”
public lecture at California Institute of Technology,
by John Preskill
4. “Schrodinger’s Phelosophy of Quantum Mechanics”,
book by Michel Bitbol, volume 188, 1996
5. “How Entanglement-Generating Satellites Will Make
the Quantum Internet Global” article in MIT
Technology Review, October 30 2014
6. “Explorations in Quantum Computing” book by
Williams, C.P, published by Springer, 2011

36. References
7. “Introduction to Reversible Logic Gates & its
Applications”, Report by Prashant R. Yelekar &
Prof. Sujata S. Chiwande, 2nd National
Conference On Information and Communication
Technology 2011
8. “Design of Reversible Sequential Circuits
Optimizing Quantum Cost, Delay, and Garbage
Outputs”, Report by Himanshu Thapalyal &
Nagarjan Ranganathan, University of South
Florida