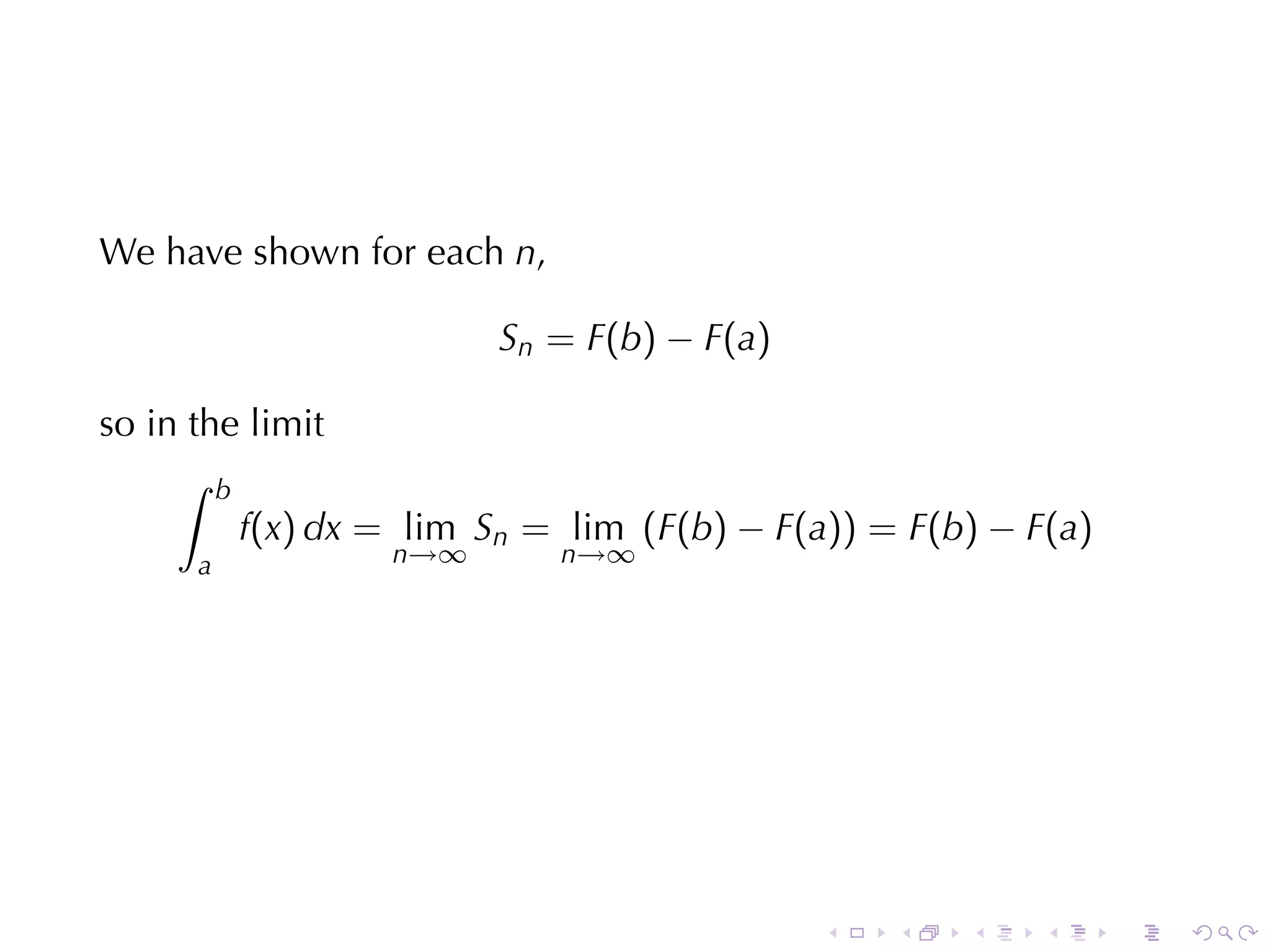Embed presentation
Download as PDF, PPTX













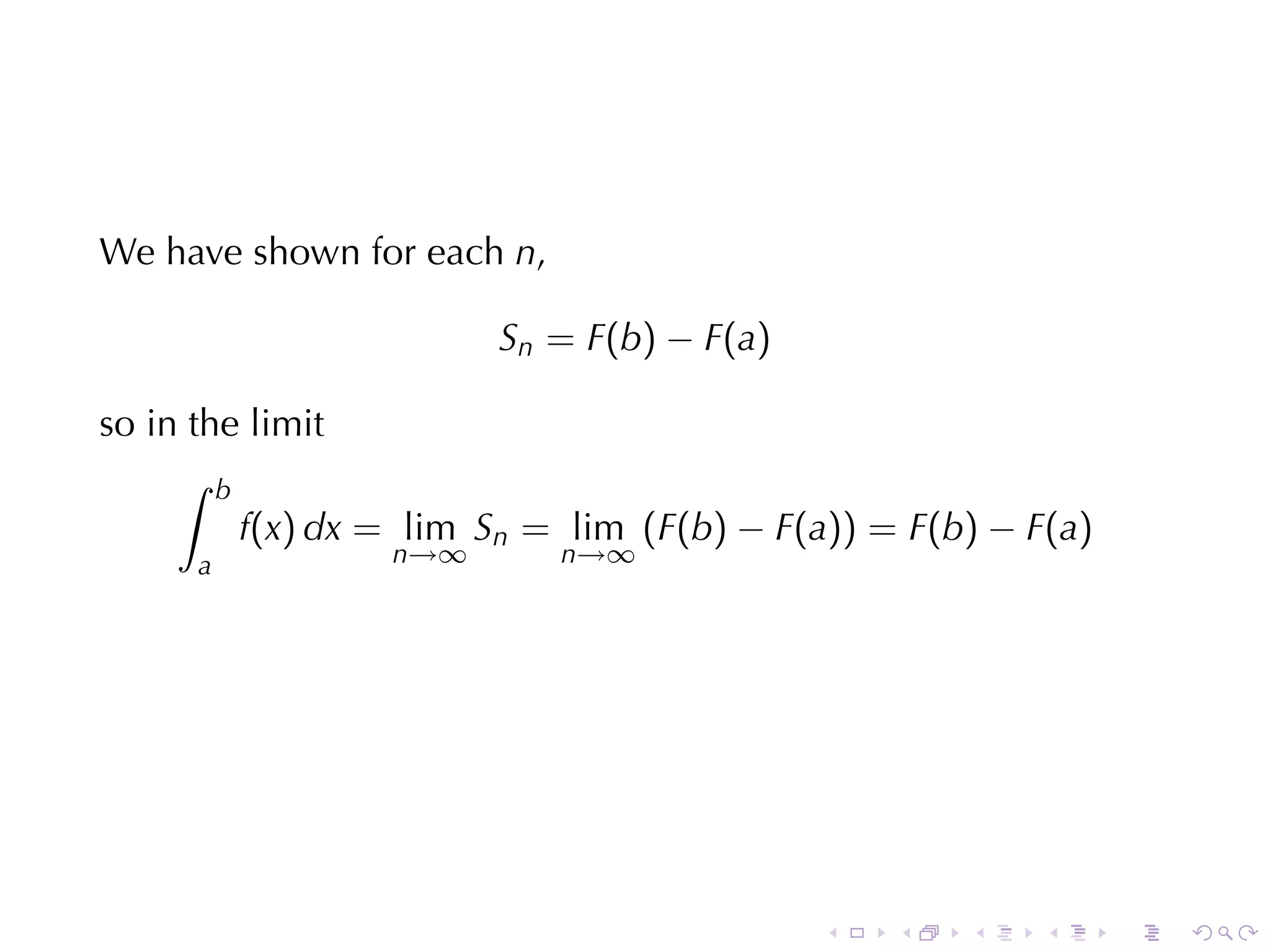
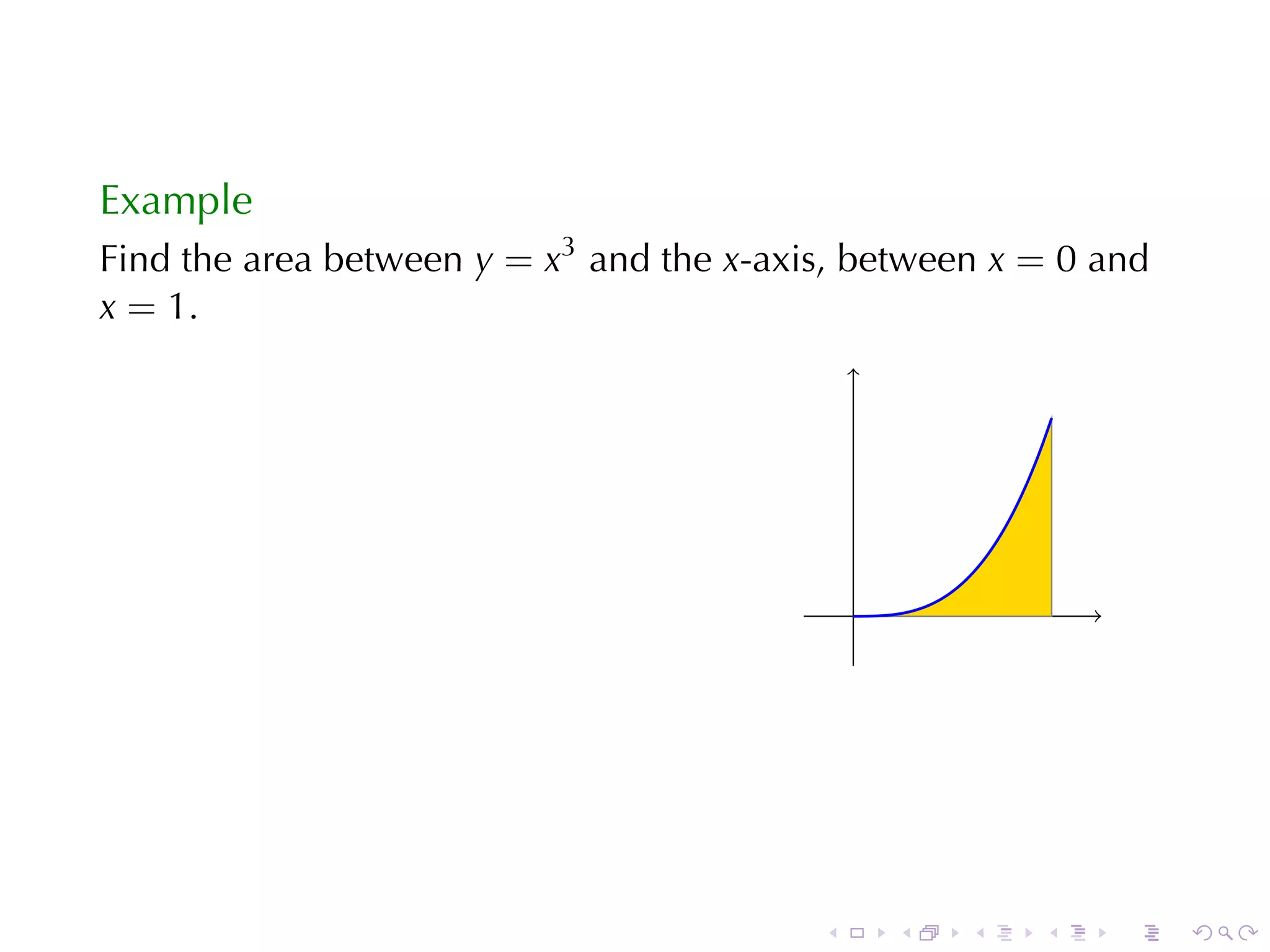
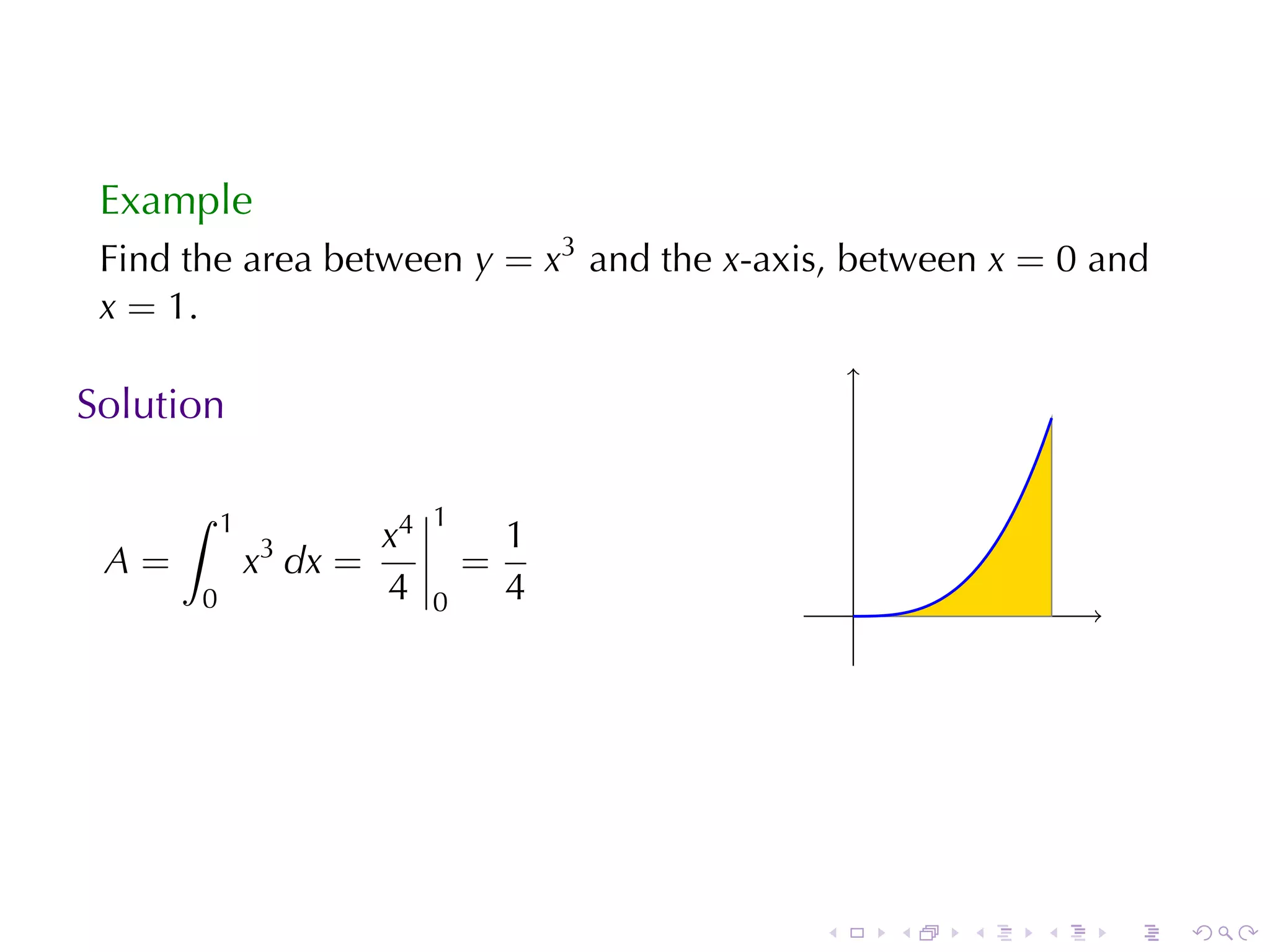
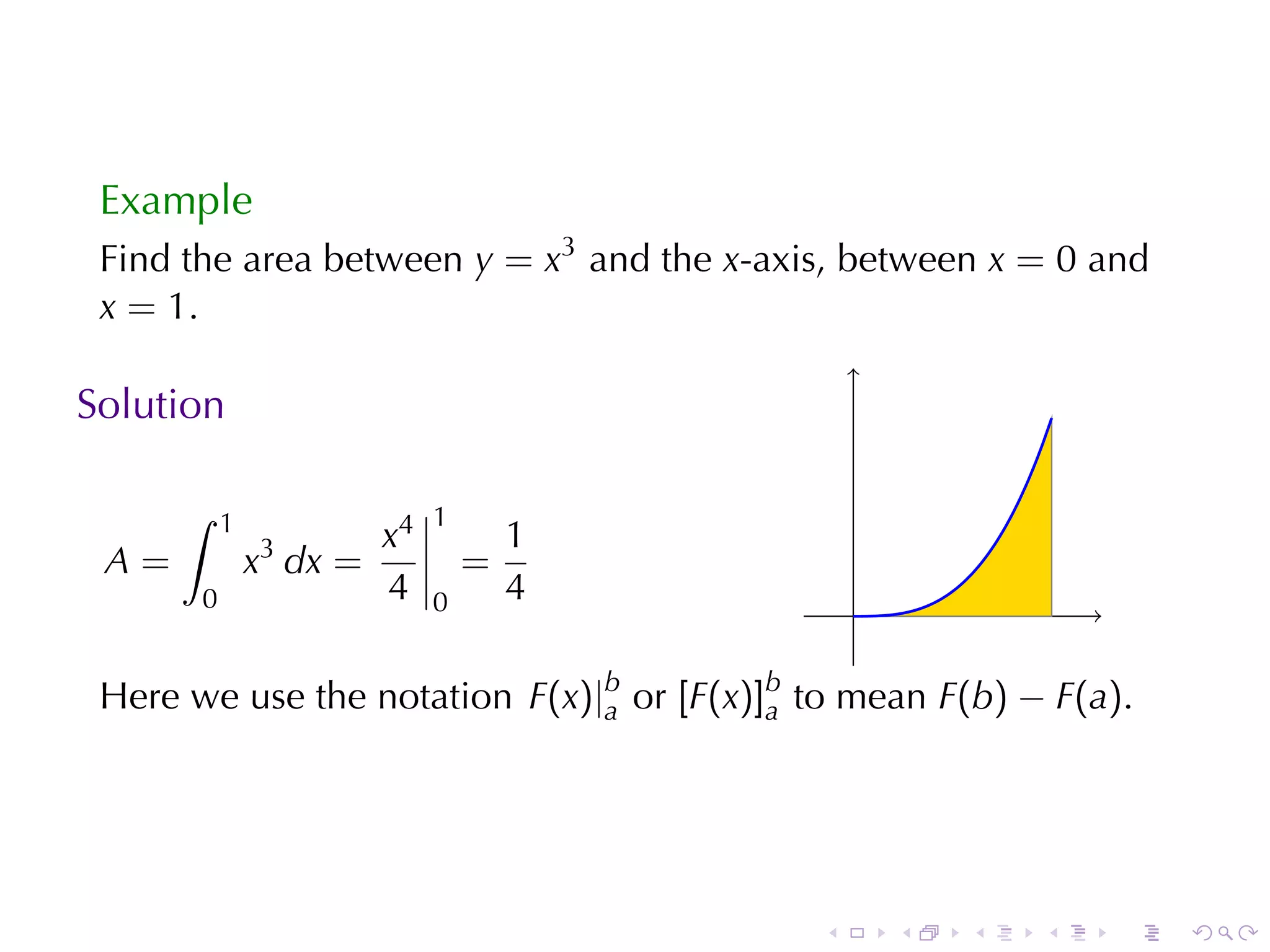

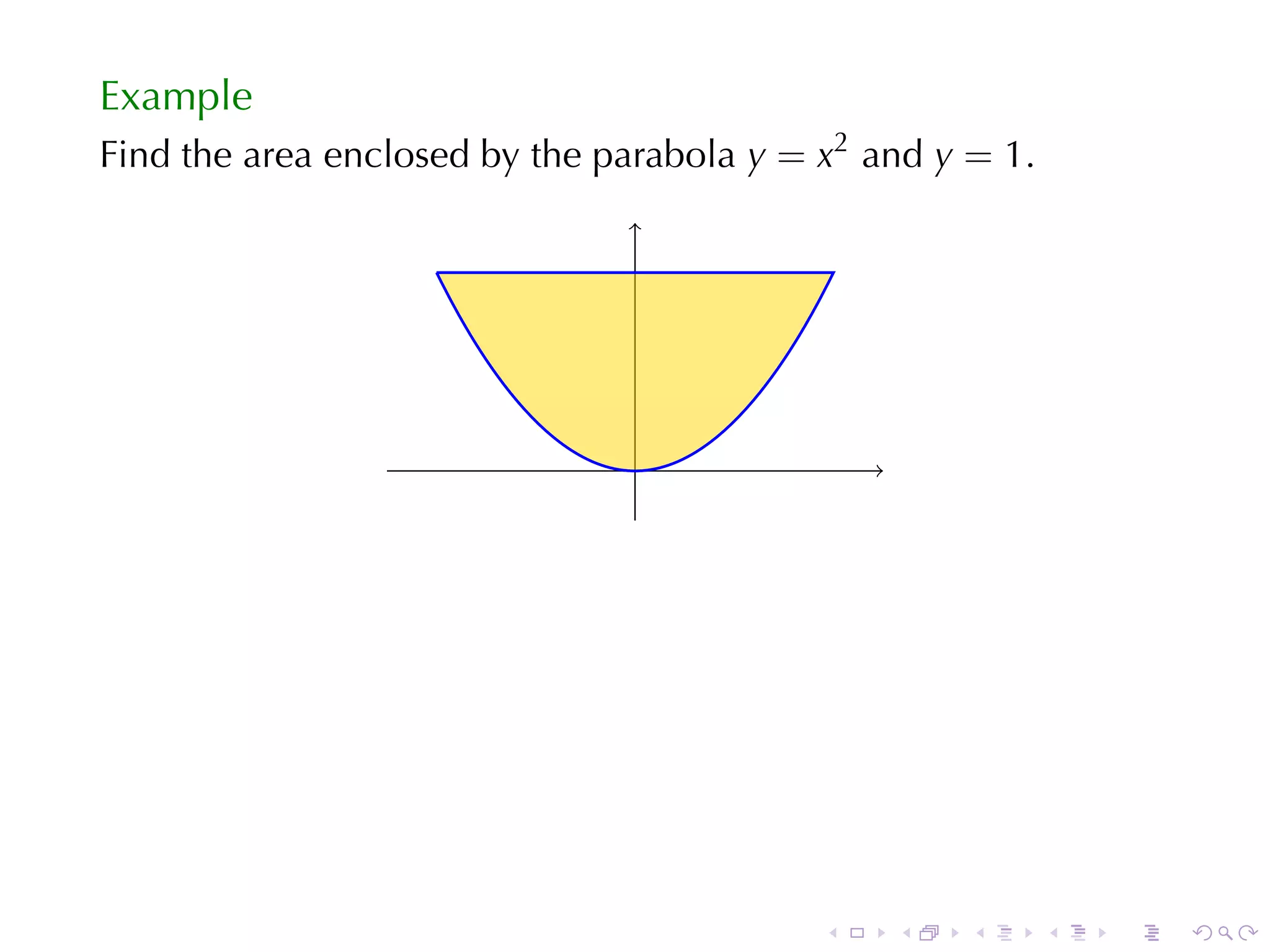













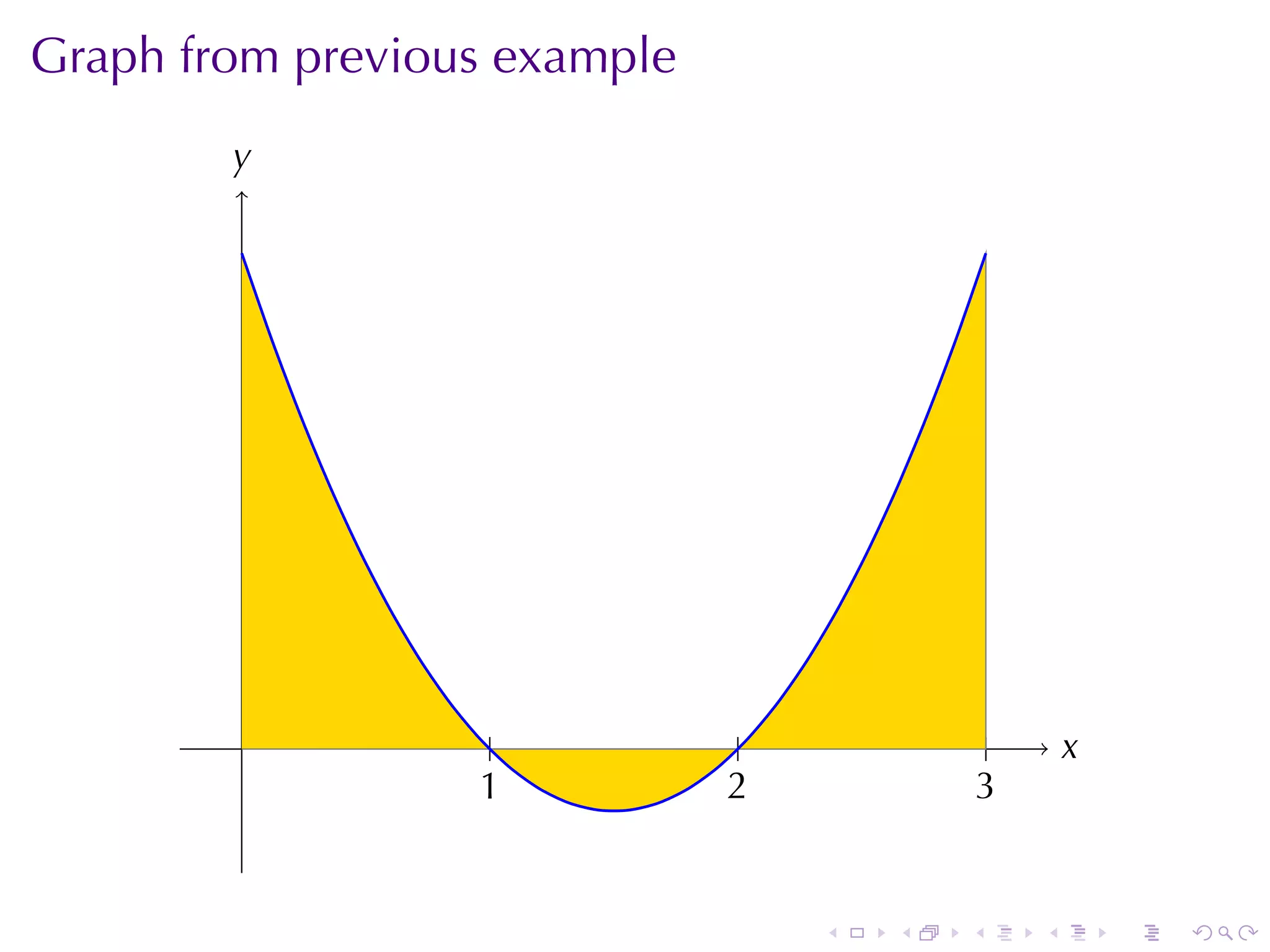


This document discusses the evaluation of definite integrals in calculus, including the limit definition, properties, and the second fundamental theorem of calculus. It provides examples and explanations of the relationship between integrals and total change, highlighting the importance of these concepts in calculus. The document aims to equip students with techniques for evaluating integrals and understanding their applications.