This document discusses symmetry elements and symmetry operations in group theory and chemistry. It defines the key symmetry elements - identity (E), proper rotation axes (Cn), mirror planes (σ), inversion centers (i), and improper rotation axes (Sn). It provides examples of how these elements apply to common molecular structures like water, methane, benzene, and transition metal complexes. The document also explains the different types of mirror planes and how the symmetry operations are generated from each element.

1. Department of Chemistry
Central university of rajasthan
Presentation on
SYMMETRY ELEMENTS AND SYMMETRY OPERATIONS
Submitted to :-
DR. Malli bhanuchandra
Astt. Professor
Department of chemistry
Submitted by :-
Roopendra singh madhukar
Int. M.sc. B.ed. Chemistry
2015imsbch023

2. GROUP THEORY :-
 Fundamentals of group theory are developed by Evariste Galois.
 It is the study of symmetry.
 It is purely mathematics concept which has wide applications in physical
sciences.
 When applied to Chemistry, it can be used, for example,
to…….
 to predict whether or not a molecule has a dipole moment
 to predict if a molecule will show optical activity
 To derive selection rules for spectroscopic transitions
 to determine which AOs to be used to construct hybrid orbitals.
 to predict which molecular vibrations lead to IR spectra.
 to label and designate MOs
 etc.

3. What is symmetry ?
 Symmetry is when a shape looks identical to its original shape
after being flipped or turned.
 Nature loves symmetry
 Most objects found in nature have symmetry
 Symmetry is associated with beauty
e.g. Flowers, diamonds, butterflies, snail shells,leaves, etc
are all beautiful, highly symmetrical because of
harmony and attractiveness of their
forms and proportions.

4. Symmetry in nature :-

5. Symmetry in the human body :-
A flower, crystal or a molecule, is said to have symmetry if it has two or
more orientations in the space that are indistinguishable. The criteria
for
Judging these are based on symmetry elements and symmetry

6. What is symmetry element and symmetry operation ?
 A symmetry element is a geometrical entity such
as a line, a plane, or a point about which one can
perform an operation of rotation, reflection, or
inversion.
 A symmetry operation is movement of a
molecule/object about an symmetry element such
that resulting configuration is indistinguishable
from the original.
 A symmetry operation will transform a molecule
into an equivalent or identical configuration.
for example:- H2O molecule is rotated about an
axis through oxygen atom and bisecting H-O-H
bond angle, through 180.
0
C2
a b b a a b
I II III

7.  The configurations I, II and III are
indistinguishable, therefore this operation is a
symmetry operation.
 The symmetry element is the imaginary line
(axis).
 The symmetry operation is the rotation of a
molecule about this axis through 180.
 I and II are equivalent.
 II and III are equivalent.
 But I and III are identical.
0

8. Symmetry elements and symmetry operations :-
Symmetry Elements Symmetry Operations
1. Identity [E] Doing nothing
2. Proper Rotation axis or
Axis of Symmetry [Cn]
Rotation about the axis through
some
angle
3. Mirror Plane or
Plane of Symmetry []
Reflection about the plane
4. Inversion Centre or
Centre of Symmetry [ i ]
Inversion
{ inversion is a reflection about a
point}
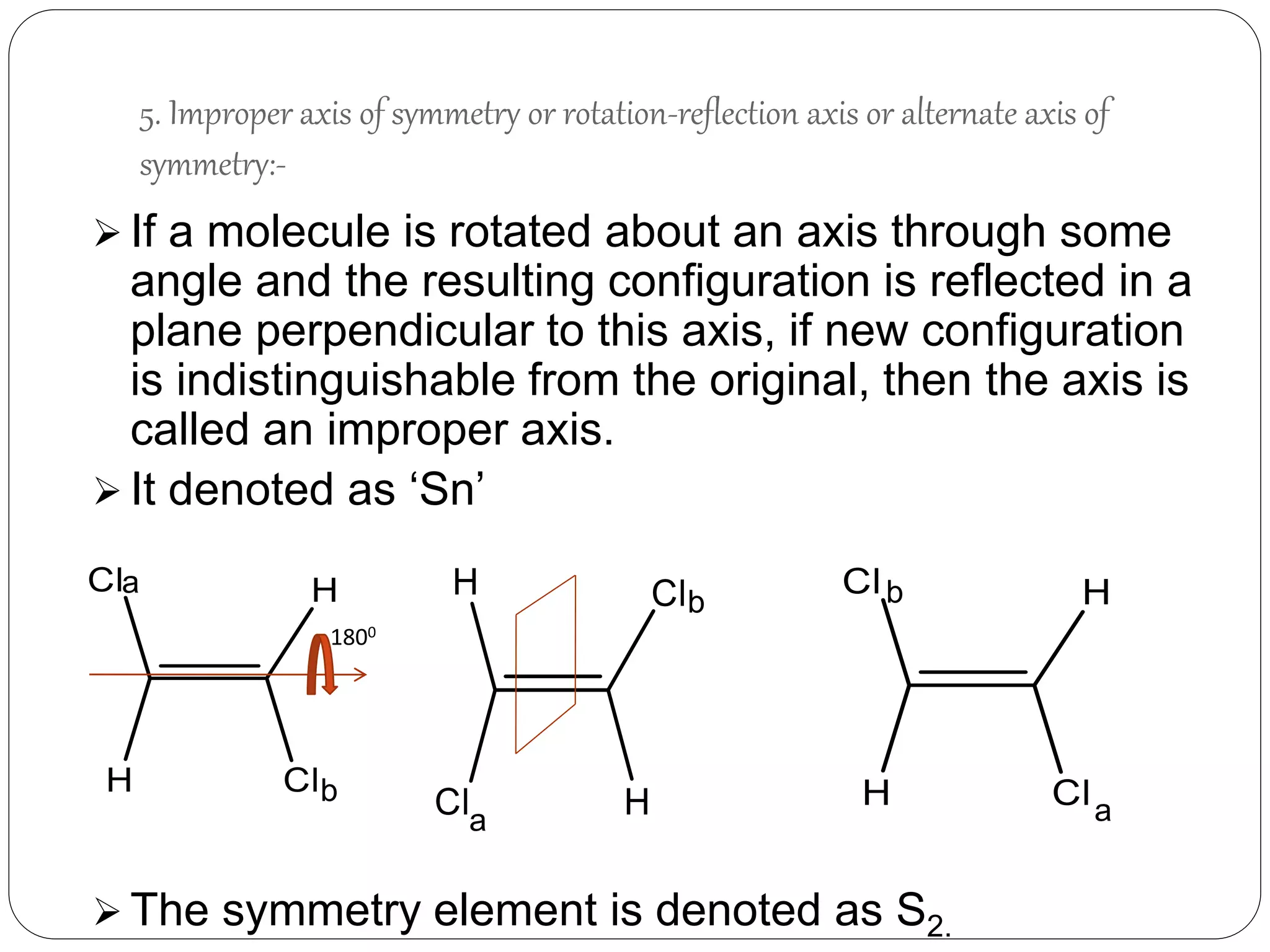
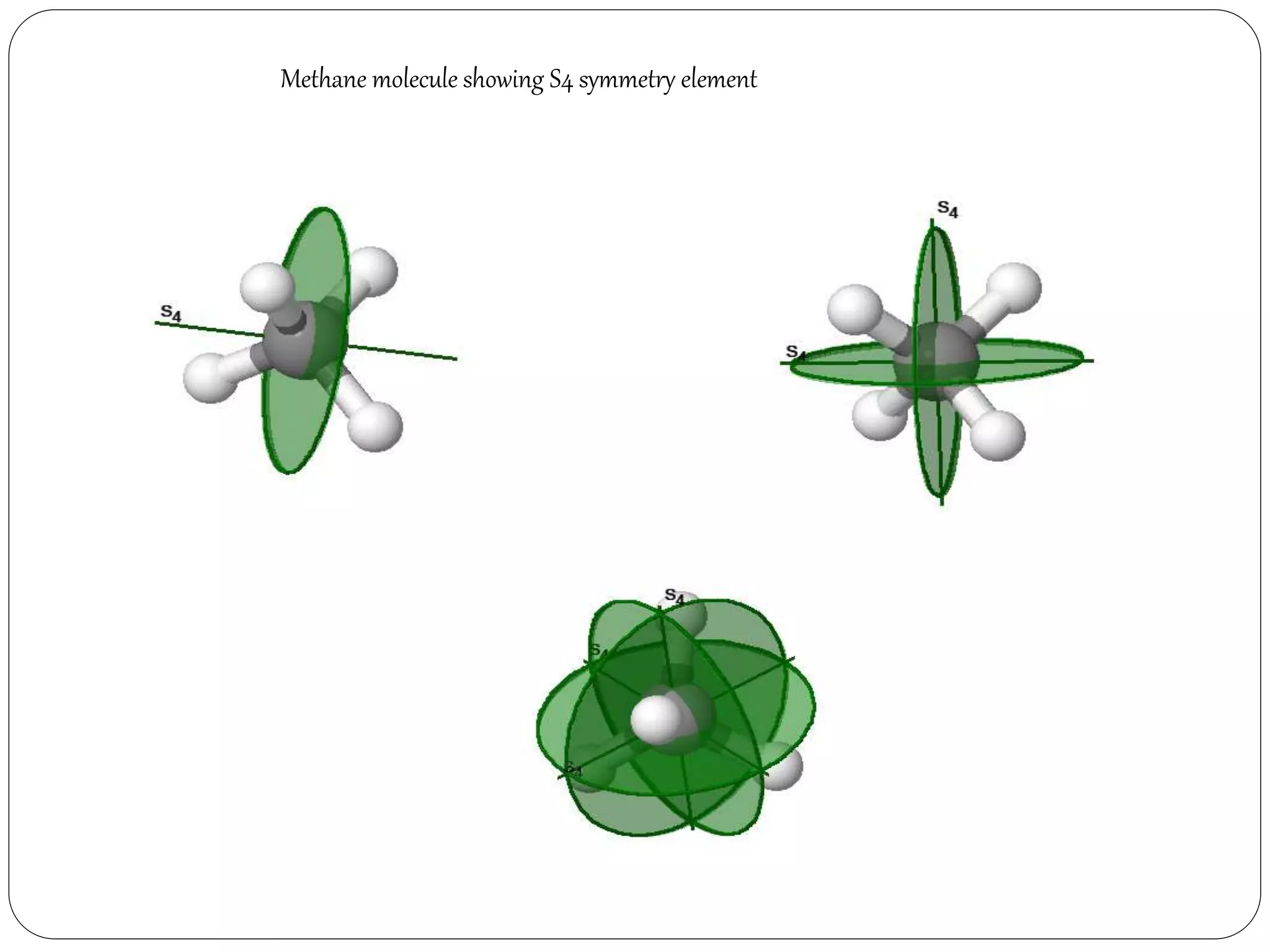
5. Improper Rotation axis or
Rotation- Reflection axis [Sn]
Rotation about an axis through
some
angle followed by a reflection in
a plane

9. 1. Identity [E] :-
 This is an operation which brings molecule back
to its original orientation.
 This operation does nothing. It is simplest of all
the symmetry elements.
 It is the only element/operation possessed by all
molecules.
 It is denoted by E.
for example:- CHBrFCl

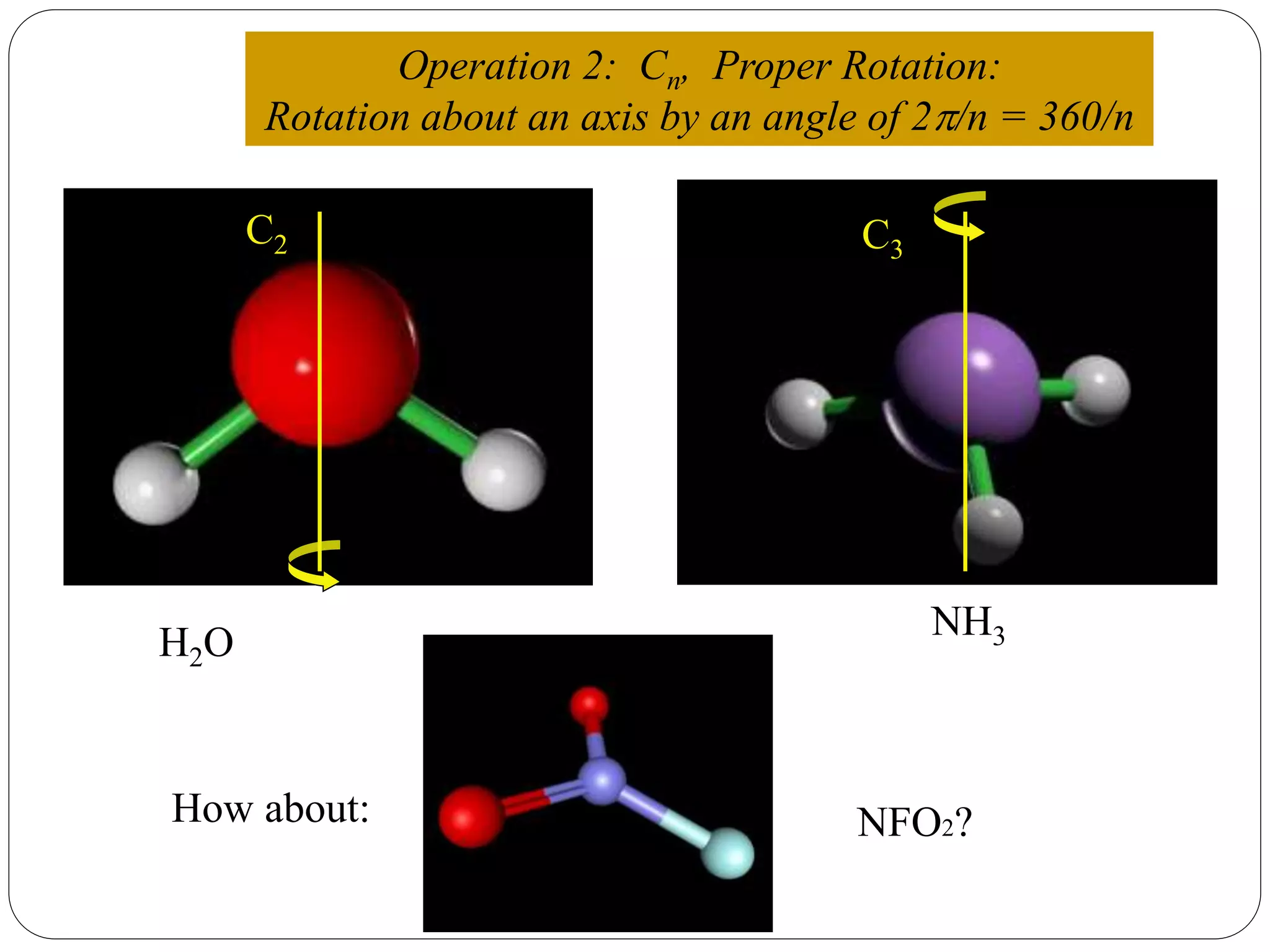
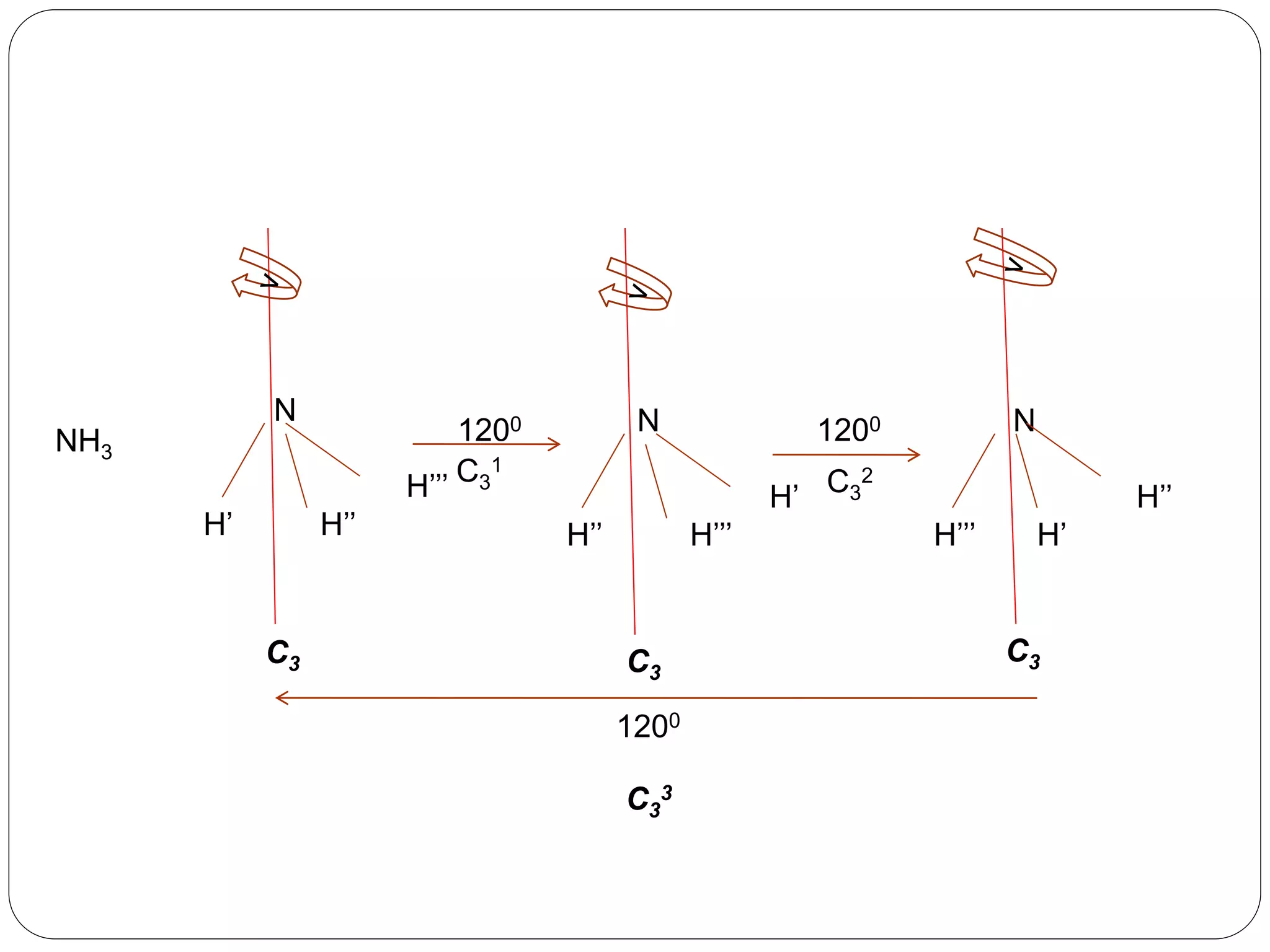
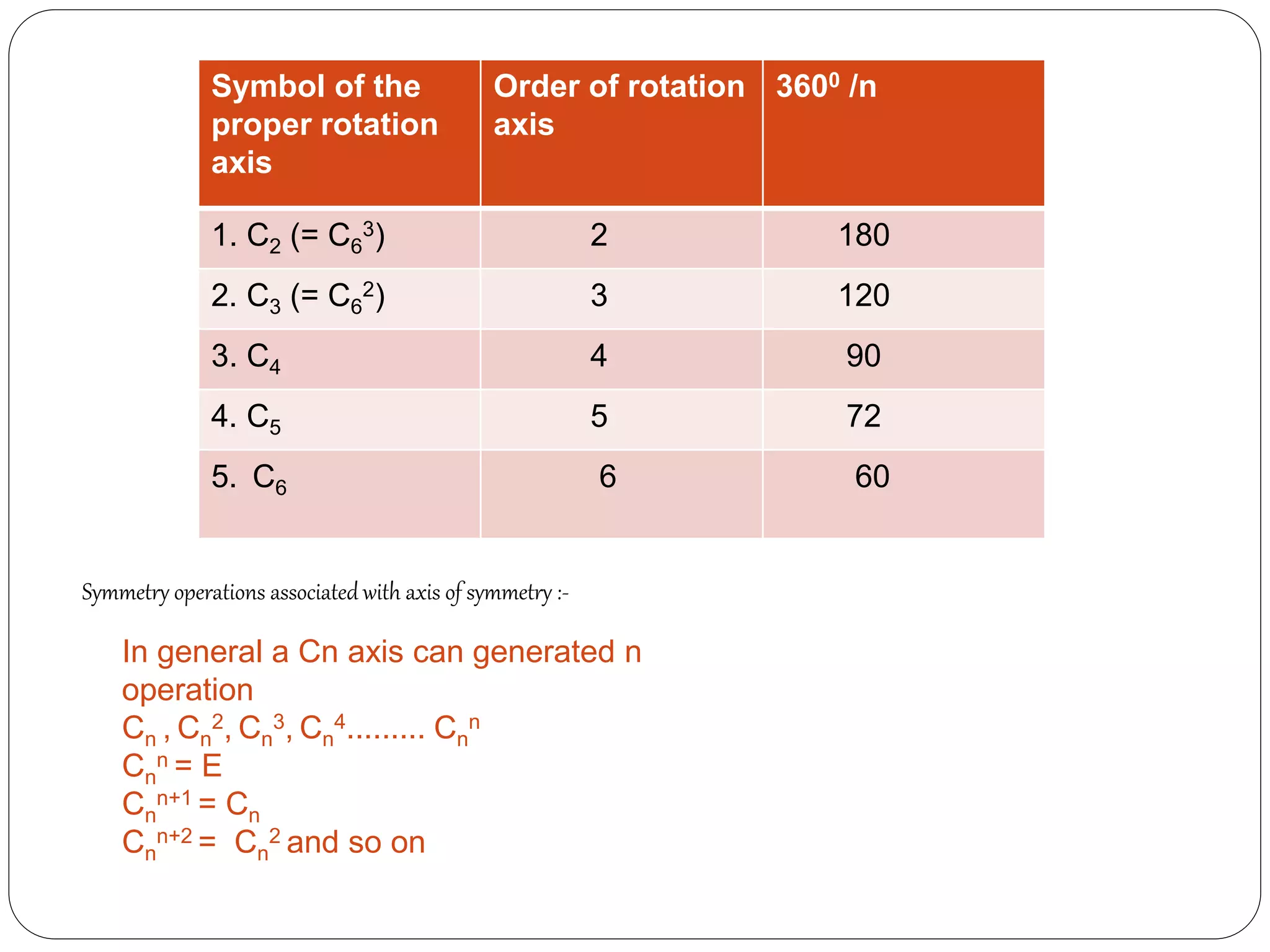
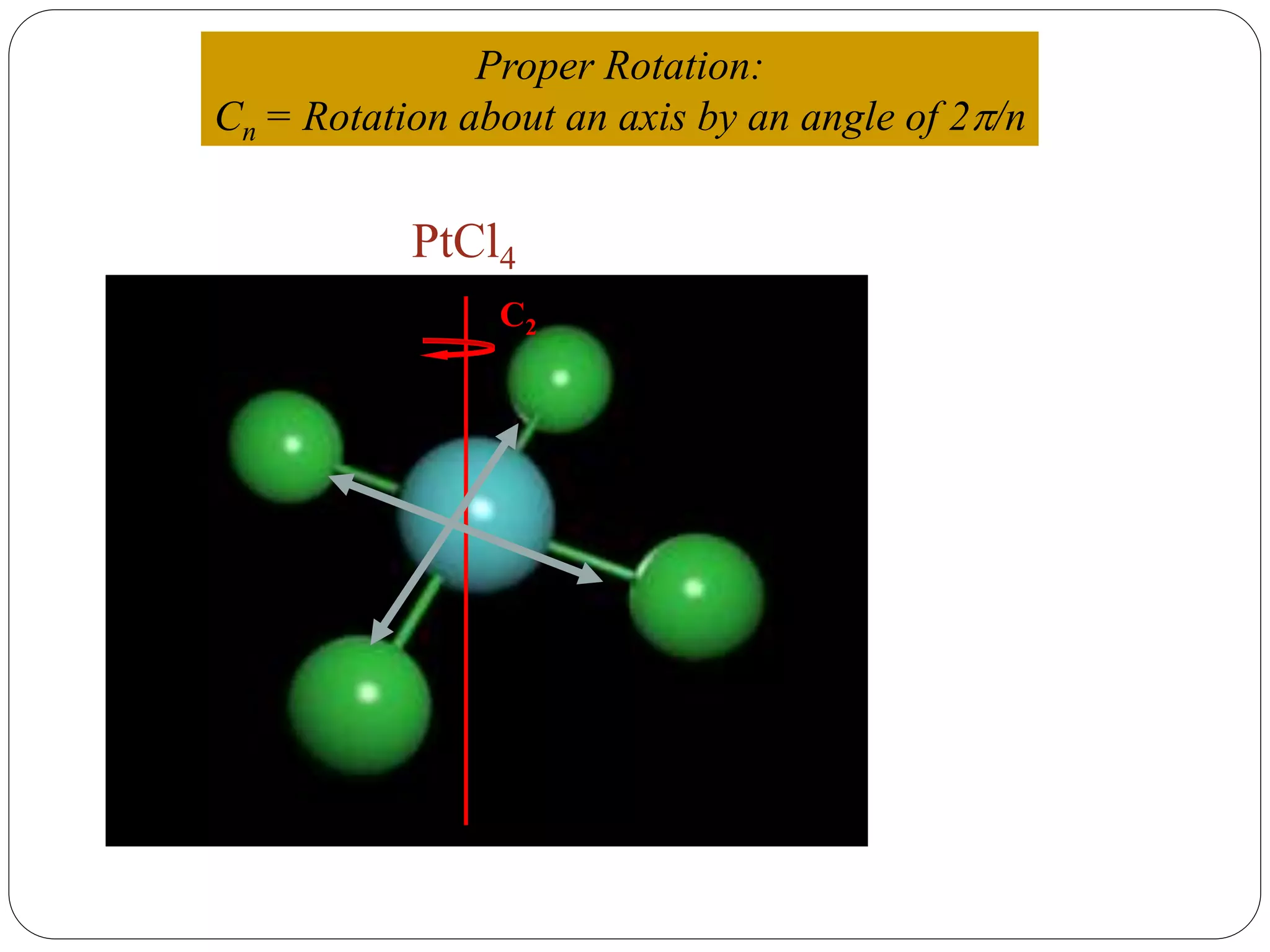
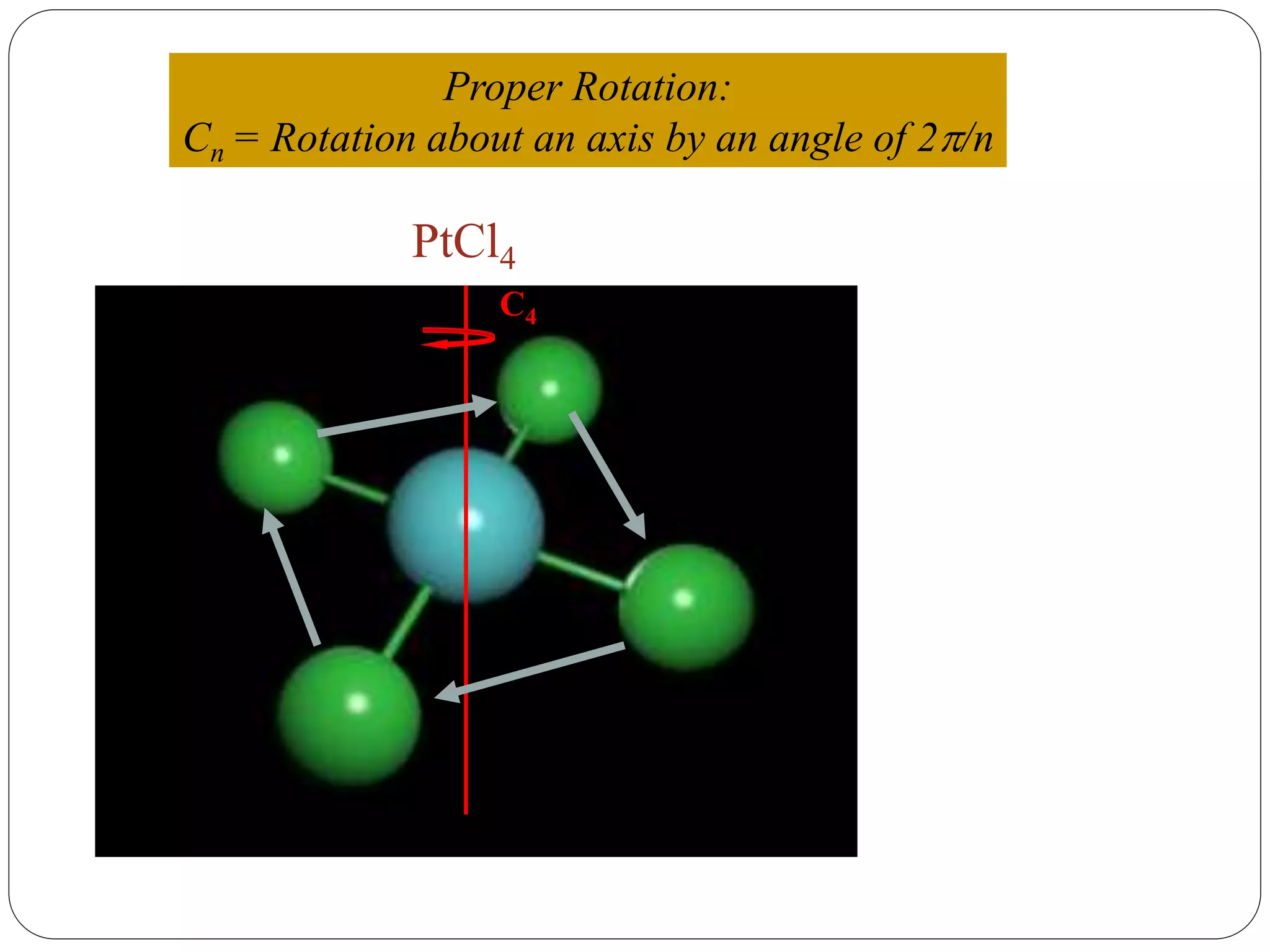
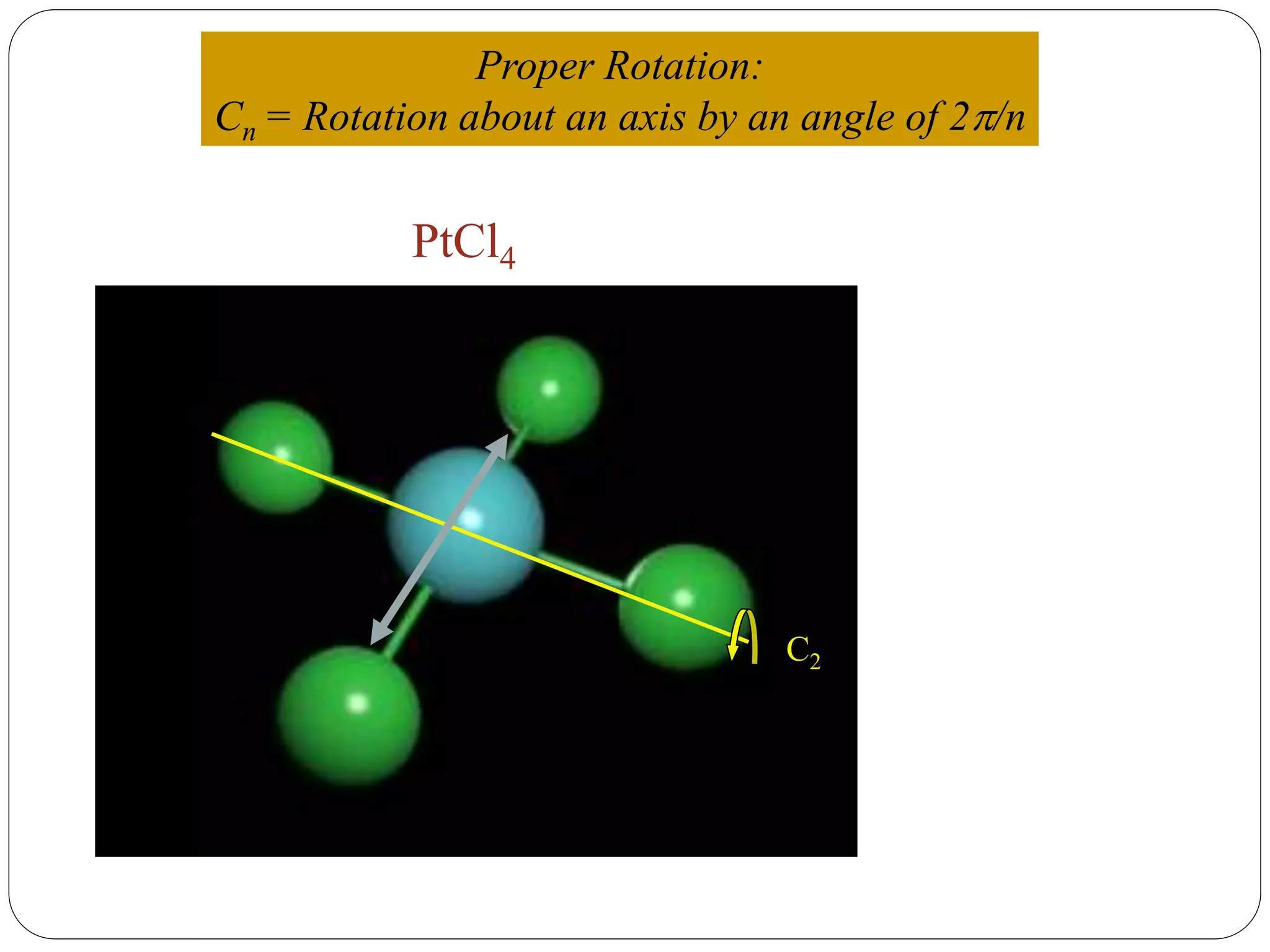
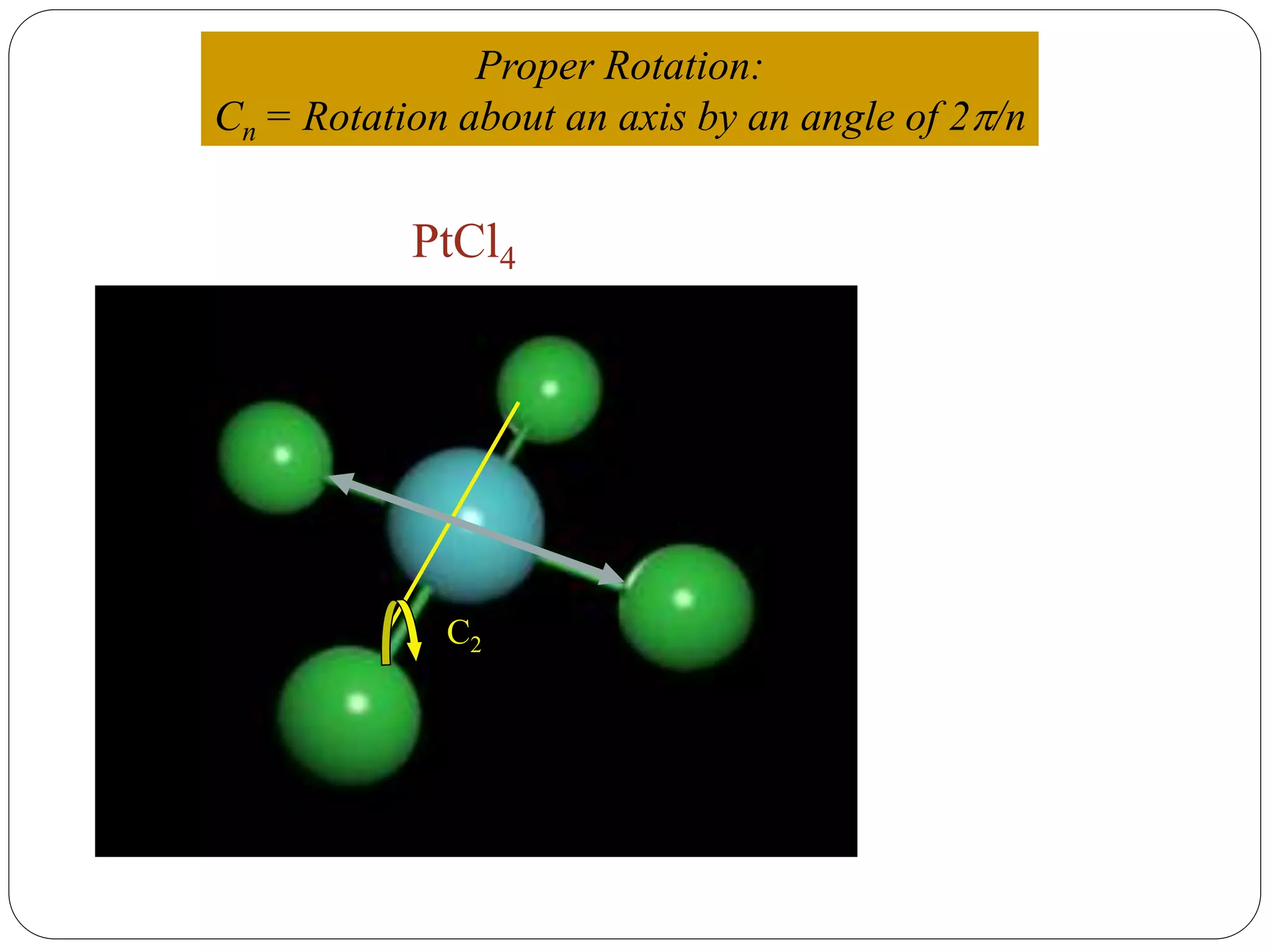
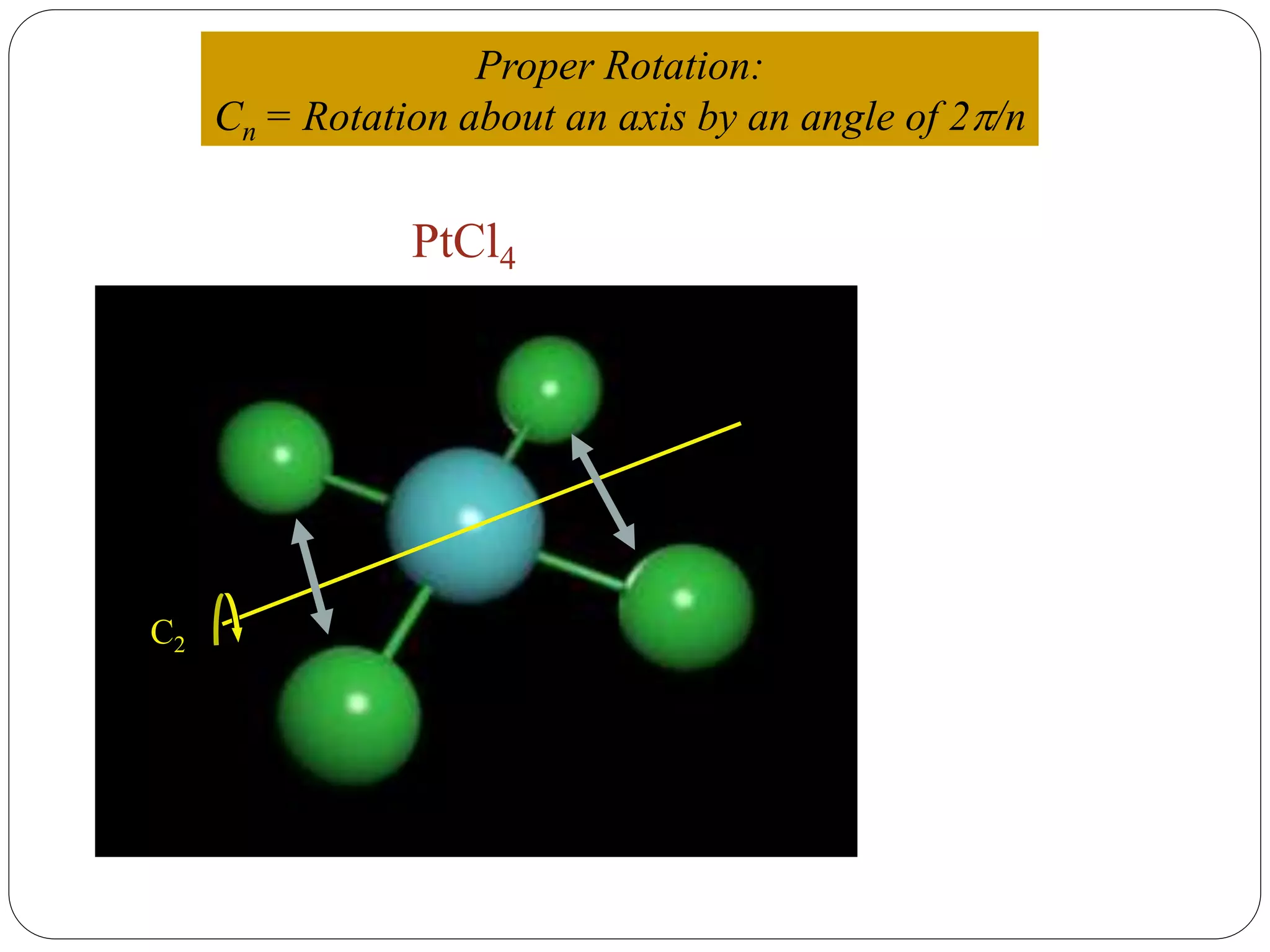
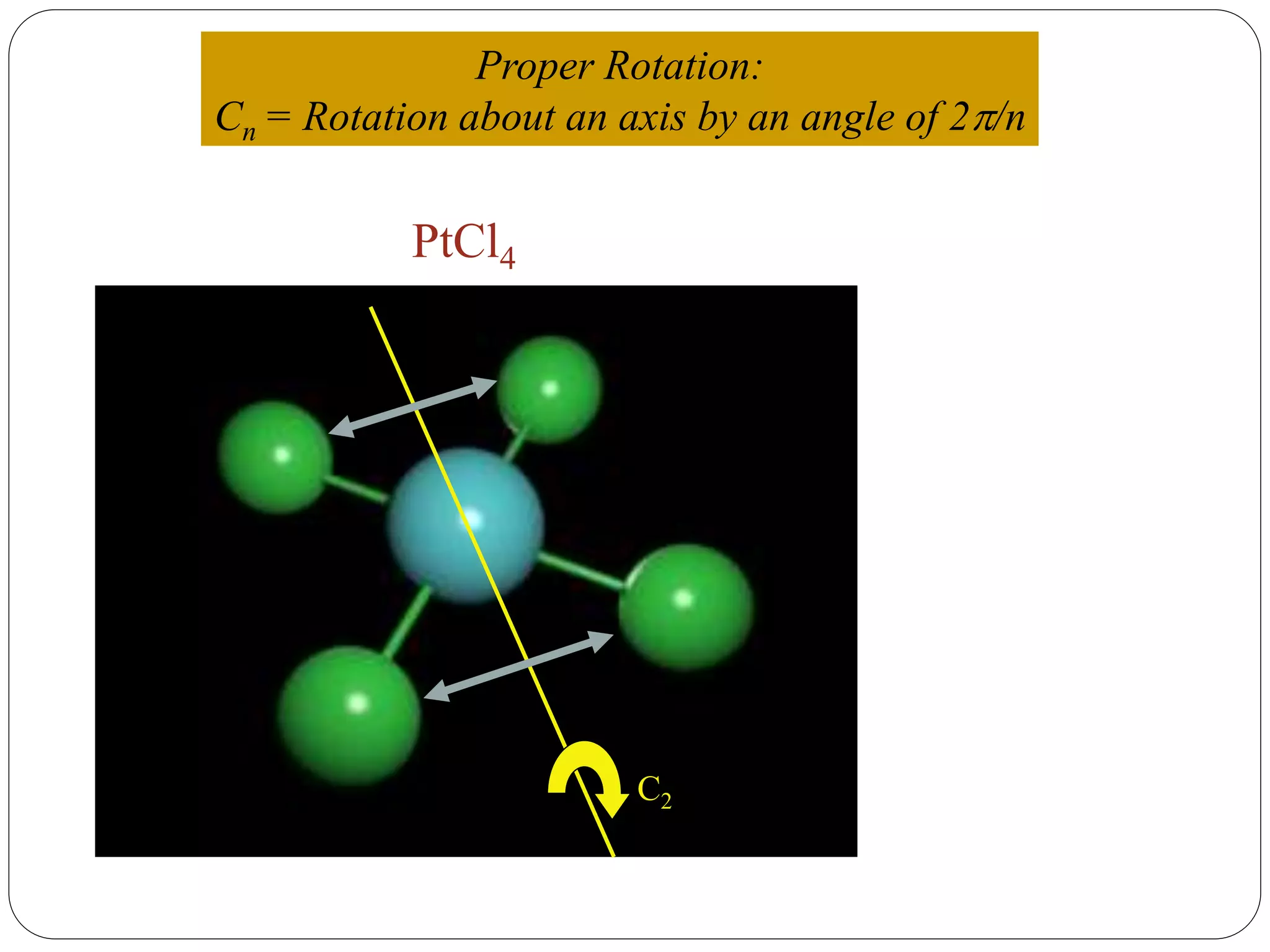
10. 2. Axis of symmetry [Cn] :-
 It is called n-fold rotational axis.
 If the rotation of a molecule about an axis through
some angle results in a configuration which is
indistinguishable from the original, then the
molecule is said to possess a proper rotation
axis.
 It is denoted as Cn.
 n is order of rotation axis.
 Rotation about an axis by an angle of 360/n.
For example:- water molecule
a b
b a1800
Order of rotation axis = 2
Symmetry element = C2 axis
Operations = C2
1, C2
2 = E

11. Operation 2: Cn, Proper Rotation:
Rotation about an axis by an angle of 2/n = 360/n
How about: NFO2?
H2O NH3
C2 C3

12. NH3
N
H’’’
H’ H’’
N
H’
H’’ H’’’
N
H’’
H’’’ H’
C3
1200 1200
1200
C3
C3
C3
1
C3
2
C3
3

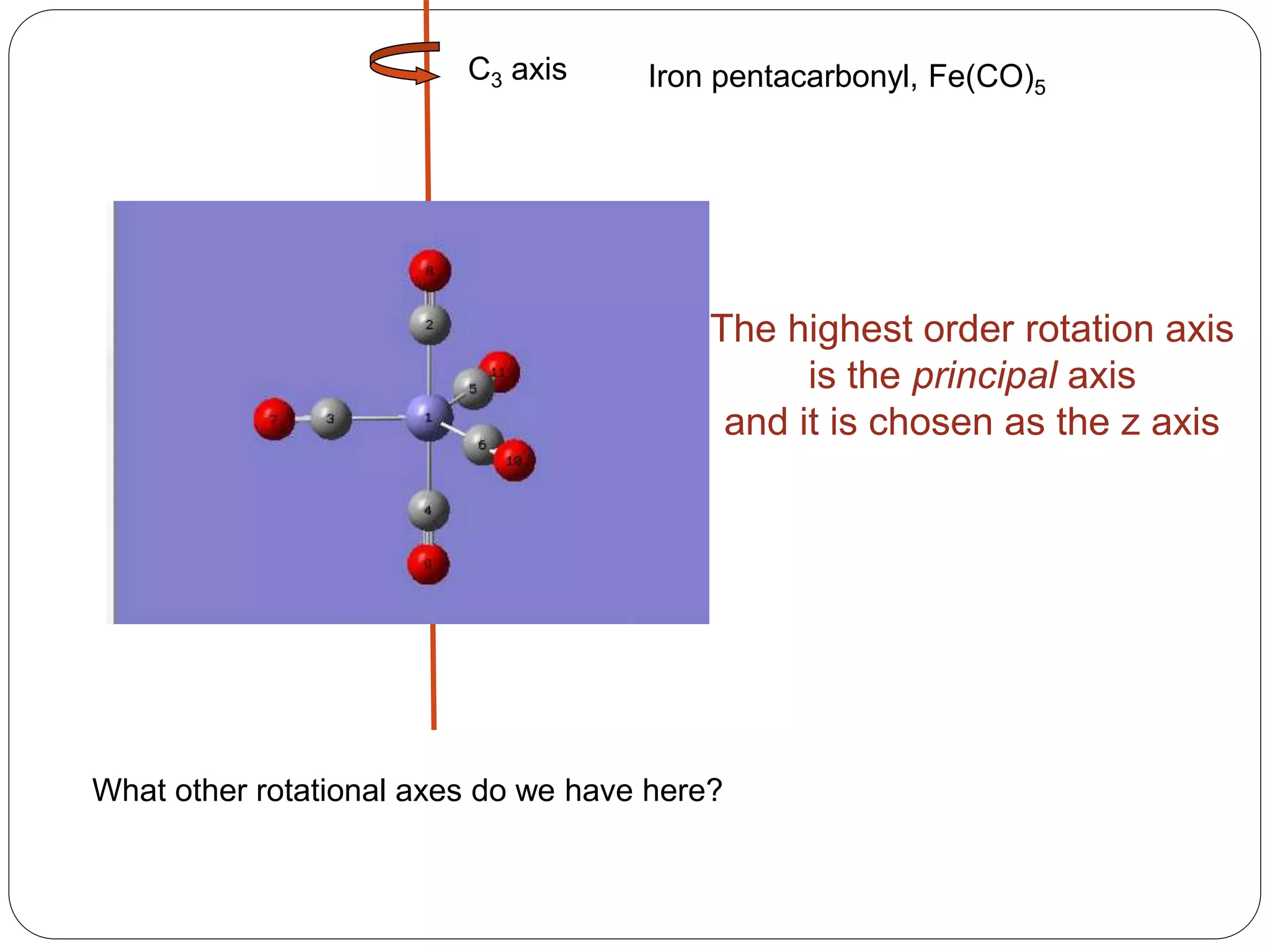
13. BF3
F
B F
F
Ni
C3 C4 C6
F
B F
F
Niv
3 C2
4 C2 6 C2
Ni[CN]4 C6H6

14. Principal and SubsidiaryAxes :
 In molecules with more than one axis of symmetry, the axis with the highest fold
symmetry (highest n in Cn) is called the Principal Axis. The other axes are called
Subsidiary Axes.
 In case there are more than one axes of same order, the axis passing through
maximum number of atoms is the Principal Axis.
 The axis of symmetry can be C∞ .
H Cl H H C∞
HCl H2

15. Symbol of the
proper rotation
axis
Order of rotation
axis
3600 /n
1. C2 (= C6
3) 2 180
2. C3 (= C6
2) 3 120
3. C4 4 90
4. C5 5 72
5. C6 6 60
Symmetry operations associated with axis of symmetry :-
In general a Cn axis can generated n
operation
Cn , Cn
2, Cn
3, Cn
4......... Cn
n
Cn
n = E
Cn
n+1 = Cn
Cn
n+2 = Cn
2 and so on

16. C2
PtCl4
Proper Rotation:
Cn = Rotation about an axis by an angle of 2/n

17. PtCl4
Proper Rotation:
Cn = Rotation about an axis by an angle of 2/n
C4

18. PtCl4
Proper Rotation:
Cn = Rotation about an axis by an angle of 2/n
C2

19. PtCl4
Proper Rotation:
Cn = Rotation about an axis by an angle of 2/n
C2

20. C2
PtCl4
Proper Rotation:
Cn = Rotation about an axis by an angle of 2/n

21. C2
PtCl4
Proper Rotation:
Cn = Rotation about an axis by an angle of 2/n

22. The highest order rotation axis
is the principal axis
and it is chosen as the z axis
Iron pentacarbonyl, Fe(CO)5
C3 axis
What other rotational axes do we have here?

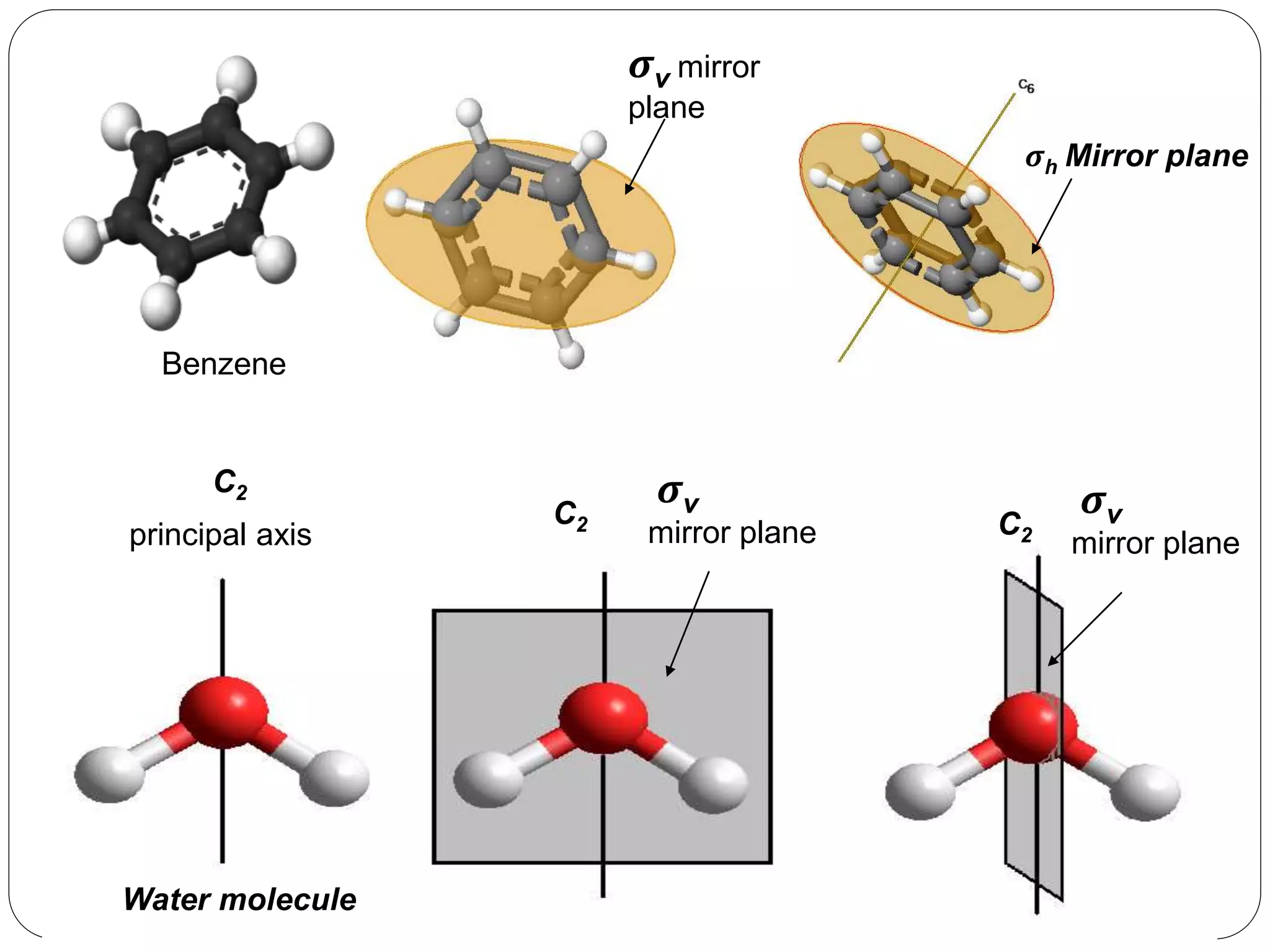
23. 3. Plane of symmetry [] :-
 A mirror plane is an imaginary plane which
divides a molecules into two equal halves such
that one half is the exact mirror image of the
other.
 It is denoted by ‘’.
 Atoms on the surface of plane remain unshifted
during reflection.
Classification of mirror planes:-
 Vertical plane(v) :- The principal axis of symmetry lies
in the this plane.
 Horizontal plane (h):- The principal axis of symmetry
is perpendicular to the plane.
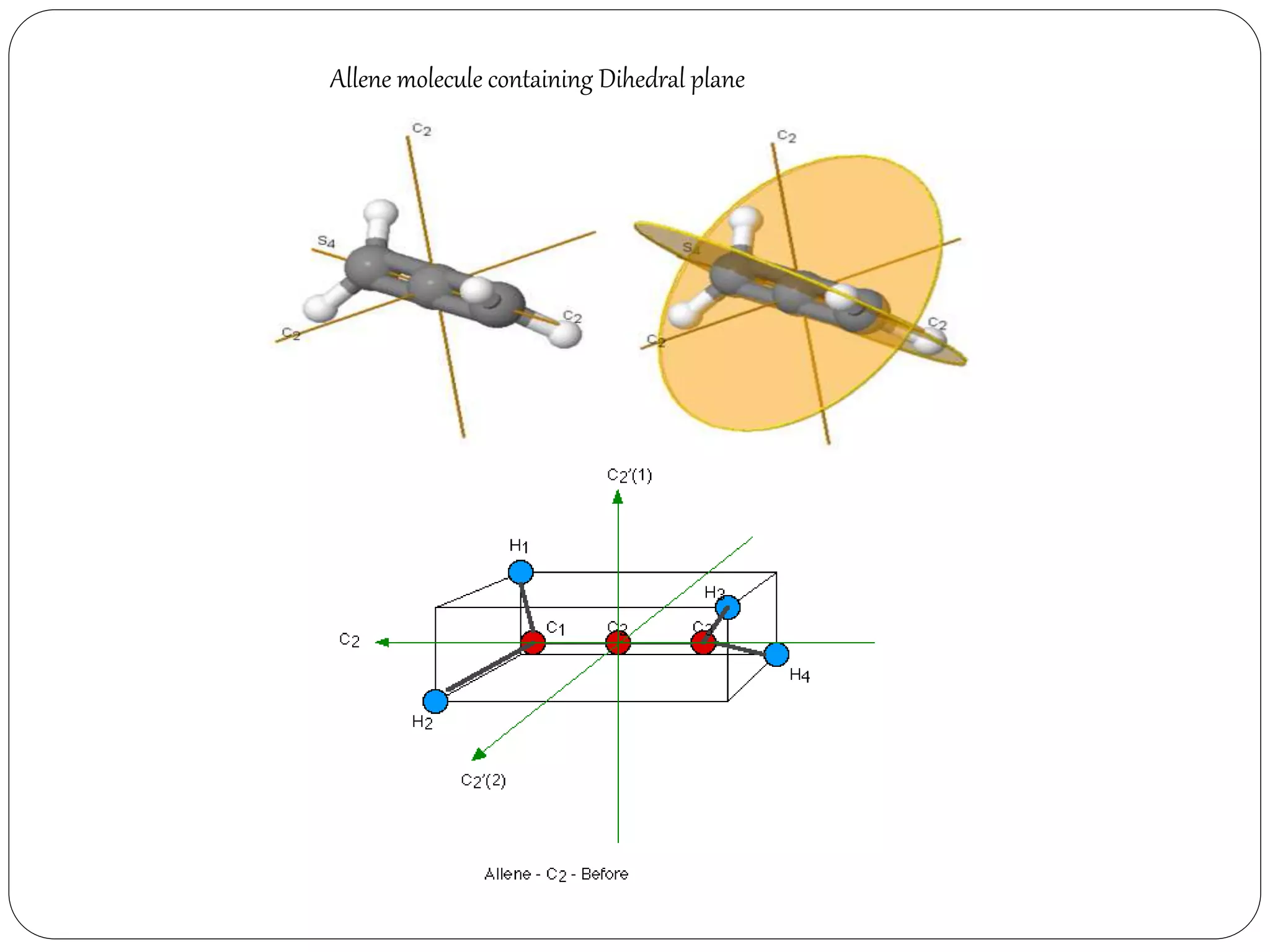
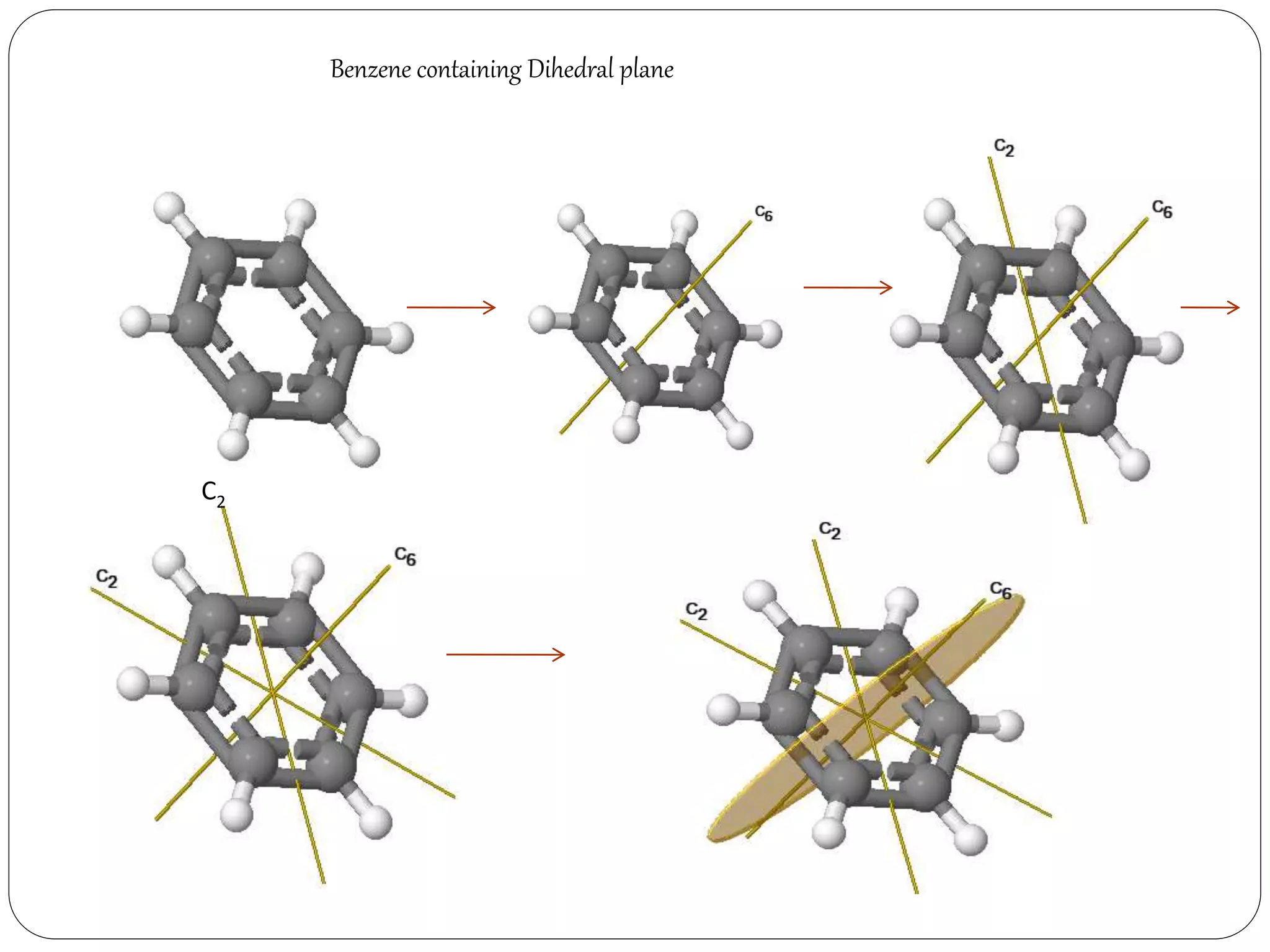
 Dihedral plane (d):- The plane passing through the
principal axis but passing in between two subsidiary
axis, is the dihedral plane.

24. C2
principal axis
C2 C2
σv
mirror plane
σv
mirror plane
σh Mirror plane
Water molecule
Benzene
σv mirror
plane

25. Allene molecule containing Dihedral plane

26. Benzene containing Dihedral plane
C2

27. 4. Inversion centre of centre of symmetry :-
 If a line drawn through a point in a molecule and
extended in both directions encounters equivalent
point in either, the point through which line is
drawn is called an inversion centre.
 It denoted as ‘i’.

28. Square planar (AB4)
Ethane
1,4-dibromobenzene
Trans-dibromoethene

29. 5. Improper axis of symmetry or rotation-reflection axis or alternate axis of
symmetry:-
 If a molecule is rotated about an axis through some
angle and the resulting configuration is reflected in a
plane perpendicular to this axis, if new configuration
is indistinguishable from the original, then the axis is
called an improper axis.
 It denoted as ‘Sn’
 The symmetry element is denoted as S2.
a
b
1800
b
a a
b

30. Methane molecule showing S4 symmetry element

31. Operations generated by Sn :-
 The no. Of operations generated by Sn depends
on whether n is odd or even.
 If ‘n’ is even then generated operations are ‘n’.
 If ‘n’ is odd then generated operations are ‘2n’.

32. References :-
 Molecular symmetry and group theory by
Robert L. Carter.
Chemical Applications of Group Theory by F.
Albert Cotton.
http://symmetry.otterbein.edu/tutorial/methane
.html
Google