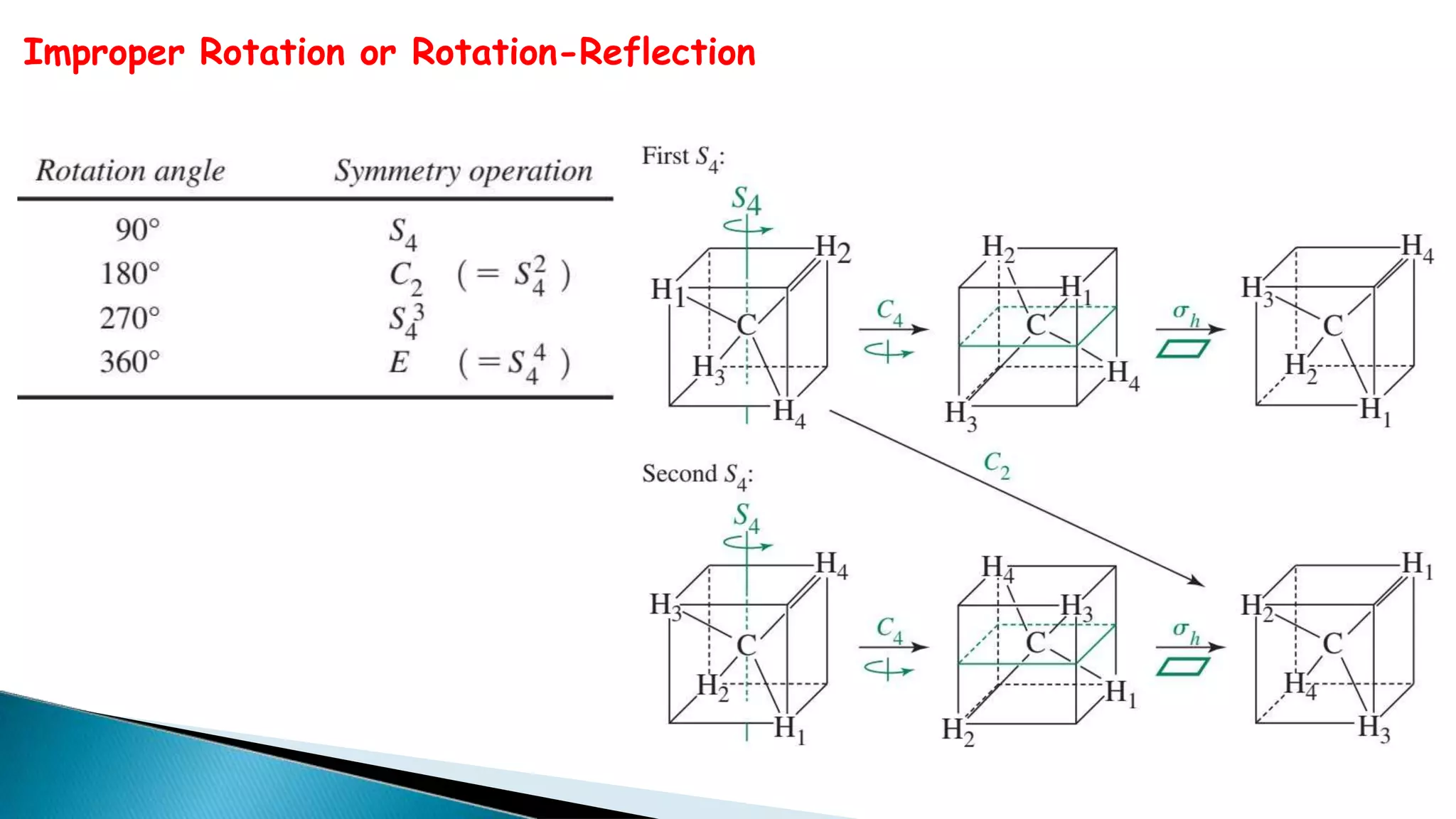
1) A symmetry operation leaves an object in an indistinguishable configuration from the original. There are five symmetry elements - n-fold rotation axis (Cn), plane of symmetry (σn), improper rotation axis (Sn), inversion center (i), and identity (E). 2) Cn rotation involves rotating around an axis by 360/n degrees. σn reflection involves reflecting through a plane. Sn rotation-reflection involves rotating and then reflecting. Inversion (i) involves reflecting through the center. 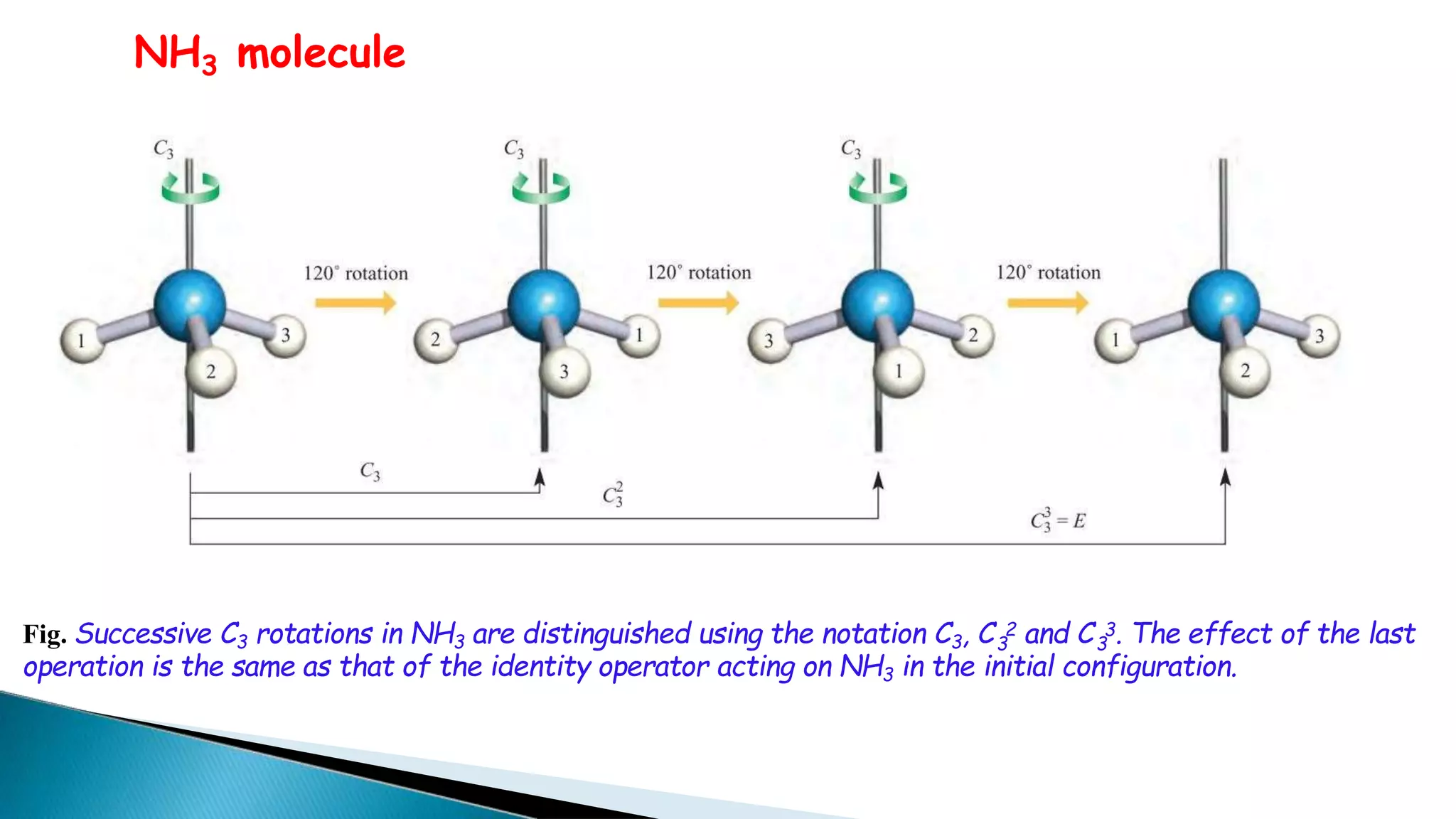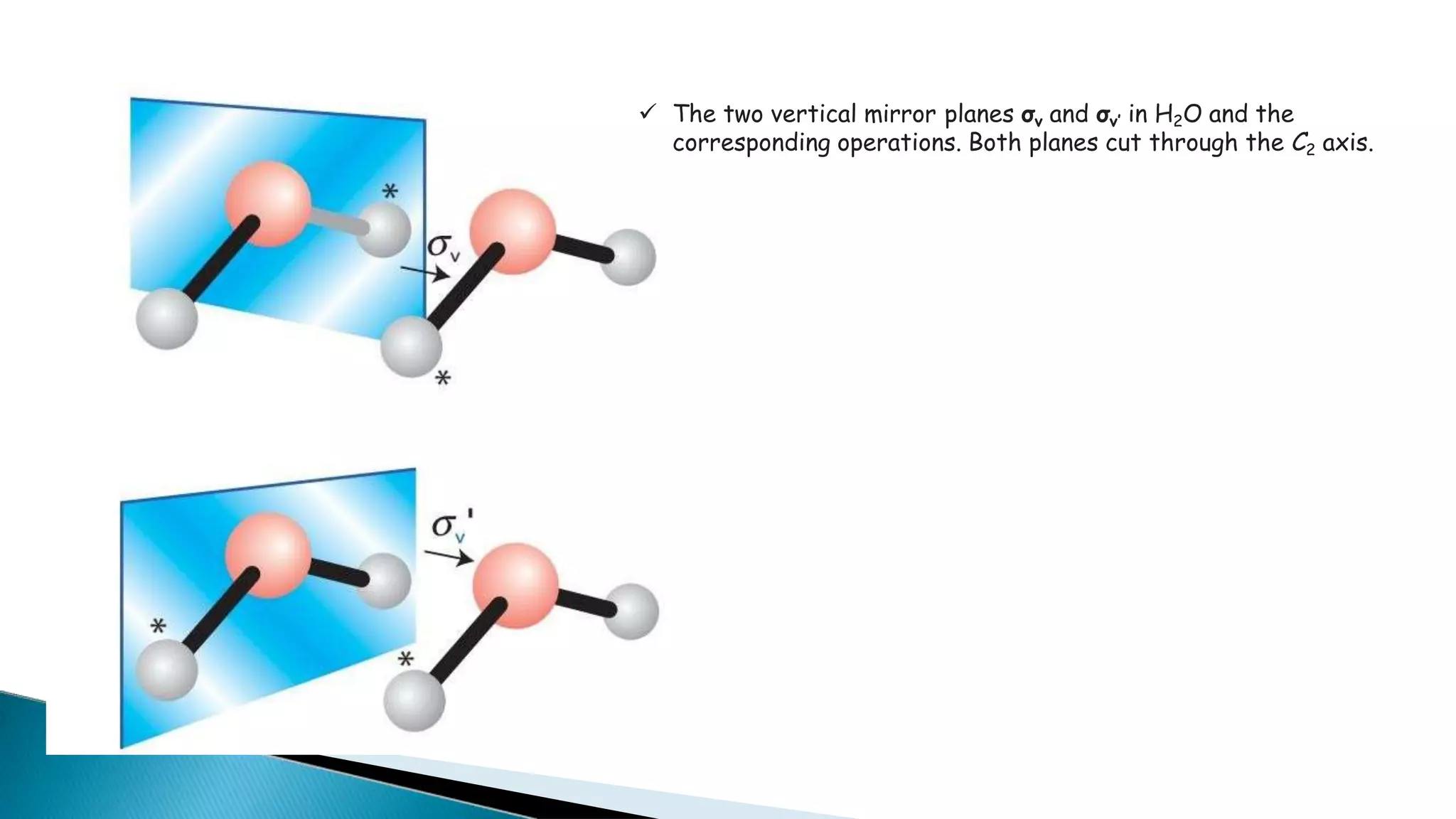3) Common molecules like water (C2), ammonia (C3), methane (C3v) demonstrate different symmetry elements and operations

1. Symmetry Elements and
Symmetry Operations
BSc -VI Sem
AE Course (CHB 673)
UNIT-II
Dr Imtiyaz Yousuf
AssistantProfessor
Department of Chemistry,
Aligarh Muslim University
Aligarh
1

2. Symmetry is all around us and is a fundamental property of nature

3. Definition
 A symmetry operation is an operation performed on an object which leaves it in a
configuration that is indistinguishable from, and superimposable on, the original
configuration.
 A symmetry operation is carried out with respect to a point, line or a plane, the latter being
called as the symmetry elements
I II III
Rotation of the trigonal planar BF3 molecule through 1200 generates a representation of the structure
that is indistinguishable from the first; one F atom is marked in red simply as a label.
A second 1200 rotation gives another indistinguishable structural representation.
Thus configurations I, II and II are Equivalent &
if we rotate III again by 1200, we will get an identical configuration to I

4. Elements of Symmetry
A symmetry element is an imaginary line, plane or a point about which a
symmetry operations are performed
There are total of five elements of symmetry and they are
1.n-proper axis of symmetry, Cn; (Rotation about an n-fold axis of
symmetry)
2.Plane of symmetry, σn ; (Reflection through a plane of symmetry (mirror
plane)
3.Improper Axis of Rotation or Rotation-Reflection axis of symmetry, Sn;
(Rotation about an axis followed by reflection through a plane perpendicular
to this axis)
4.Inversion centre (i); (Reflection through a center of symmetry)
5.The Identity (E); Do nothing to the molecule

5. 1. Rotation about an n-fold axis of symmetry (Cn)
Symmetry Operation = Rotation about an n-fold axis of symmetry
The molecule is rotated along an axis such that after the rotation is performed,
the molecule possesses a configuration which is indistinguishable from that of the
original.
The symmetry operation of rotation about an n-fold axis (the symmetry element)
is denoted by the symbol Cn, in which the angle of rotation is 360/n ; n is an
integer, e.g. 2, 3, 4……
Angle of rotation = 360 /n
If a molecule possesses more than one type of n-axis, the axis of highest value of
n is called the principal axis; it is the axis of highest molecular symmetry

7. n-fold rotation - a rotation of 360°/n about the Cn axis (n = 1 to )
H (2 )
O (1 )
H (3 ) H (3 )
O (1 )
H (2 )
In water there is a C2 axis so we can perform a 2-fold (180°) rotation to get the identical arrangement
of atoms.
H (2 )
H (4 ) H (3 )
N (1 )
H (2 )
H (3 )
H (4 )
N (1 )
In ammonia there is a C3 axis so we can perform 3-fold (120°) rotations to get identical
arrangement of atoms.
H (2 )
H (3 )
H (4 )
N (1 )
120° 120°
180°

8. Fig. The 3-fold (C3) and three 2-fold (C2)
axes of symmetry possessed by the
trigonal planar BF3 molecule
Fig. The H2O molecule possesses one C2 axis and two mirror planes.
(a) The C2 axis and the plane of symmetry that contains the H2O molecule.
(b)The C2 axis and the plane of symmetry that is perpendicular to the plane
of the H2O molecule.
(c) Planes of symmetry in a molecule are often shown together on one diagram;
this representation for H2O combines diagrams (a) and (b)

9. NH3 molecule
3 3
Fig. Successive C3 rotations in NH3 are distinguished using the notation C3, C 2 and C 3. The effect of the last
operation is the same as that of the identity operator acting on NH3 in the initial configuration.

10. The square planar molecule XeF4:
(a) One C2 axis coincides with the principal (C4) axis; the molecule lies in ah plane which contains two C2’ and two
C2’’ axes.
(b) Each of the two v planes contains the C4 axis and one C2’ axis.
(c) Each of the two σd planes contains the C4 axis and one C2’’ axis

11. 2. Plane of symmetry (σn)
 Symmetry Operation = Reflection through a plane (mirror plane)
If reflection of all parts of a molecule through a plane produces an indistinguishable
configuration, the plane is a plane of symmetry; the symmetry operation is one of reflection
and the symmetry element is the mirror plane (denoted by σ).
For BF3,
 The plane containing the molecular framework (the yellow plane shown in Fig.) is a mirror
plane.
 The plane lies perpendicular to the vertical principal axis and is denoted by the symbol σh.

12.  Molecules which are in a linear, bent or planar can always be drawn in a plane, but this plane can be
labelled σh only if the molecule possesses a Cn axis perpendicular to the plane. If the plane contains the
principal axis, it is labelled σv.
 A special type of σ plane which contains the principal rotation axis, but which bisects the angle between
two adjacent 2-fold axes, is labelled σd. A square planar molecule such as XeF4 provides an example.
 XeF4 contains a C4 axis (the principal axis) and perpendicular to this is the σh plane in which the
molecule lies .
 Reflection planes may be vertical, horizontal or dihedral (more on d later).
Vertical and dihedral mirror planes of geometric shapes.
h
v
v
 Two successive reflections are equivalent to the identity operation (nothing is moved) σn = σ (n = even)
d d

13.  The two vertical mirror planes σv and σv’ in H2O and the
corresponding operations. Both planes cut through the C2 axis.

14. 3. Inversion centre (i)
 Symmetry Operation = Reflection through a centre of symmetry
If reflection of all parts of a molecule through the centre of the molecule produces an
indistinguishable configuration, the centre is called a ‘centre of symmetry’,
It also called a centre of inversion and id designated by the symbol i.
Each of the molecules CO2 , trans-N2F2 , SF6 and benzene possesses a center of symmetry.
 Each point moves through the center of the molecule to a position opposite the original
position and as far from the central point as where it started.
[x, y, z]
i
[-x, -y, -z]

15. Ethane in the
staggered
conformation
Methane

16. 4. Improper Axis of Rotation or Rotation-Reflection axis of symmetry, (Sn)
 Symmetry Operation = Rotation about an axis followed by reflection through a plane
perpendicular to this axis
If rotation through 360/n about an axis, followed by reflection through a plane perpendicular to
that axis, yields an indistinguishable configuration, the axis is an n-fold rotation–reflection axis,
also called an n-fold improper rotation axis.
 Tetrahedral species of the type XY4 (all Y groups must be equivalent) possess three S4 axes, and the
operation of one S4 rotation–reflection in the CH4 molecule
 An improper rotation (or rotation–reflection),
Sn, involves rotation about 360/n followed by
reflection through a plane that is
perpendicular to the rotation axis.
 The operation about one of the S4 axes in CH4;
 Three S4 operations are possible for the CH4
molecule

17. Improper Rotation or Rotation-Reflection

18. The identity operation (E)
 Causes no change in the molecule.
 No atom does actually change its position
 It is included for mathematical completeness.
 An identity operation is characteristic of every molecule, even if it has no other
symmetry

19. Symmetry elements Shape Examples
Symmetry elements Shape Examples
EXAMPLES

20. References
Inorganic Chemistry by Gary L. Miessler, Paul J. Fischer,
Donald A.Tarr, 5th Edition, (2014)
Inorganic Chemistry by Shriver & Atkins, 5th Edition.
Inorganic Chemistry, Principle, structure and reactivity, by J.
E. Huheey 4th edition,
Advanced Inorganic Chemistry, by Cotton & Willkinson, 5th
Edition