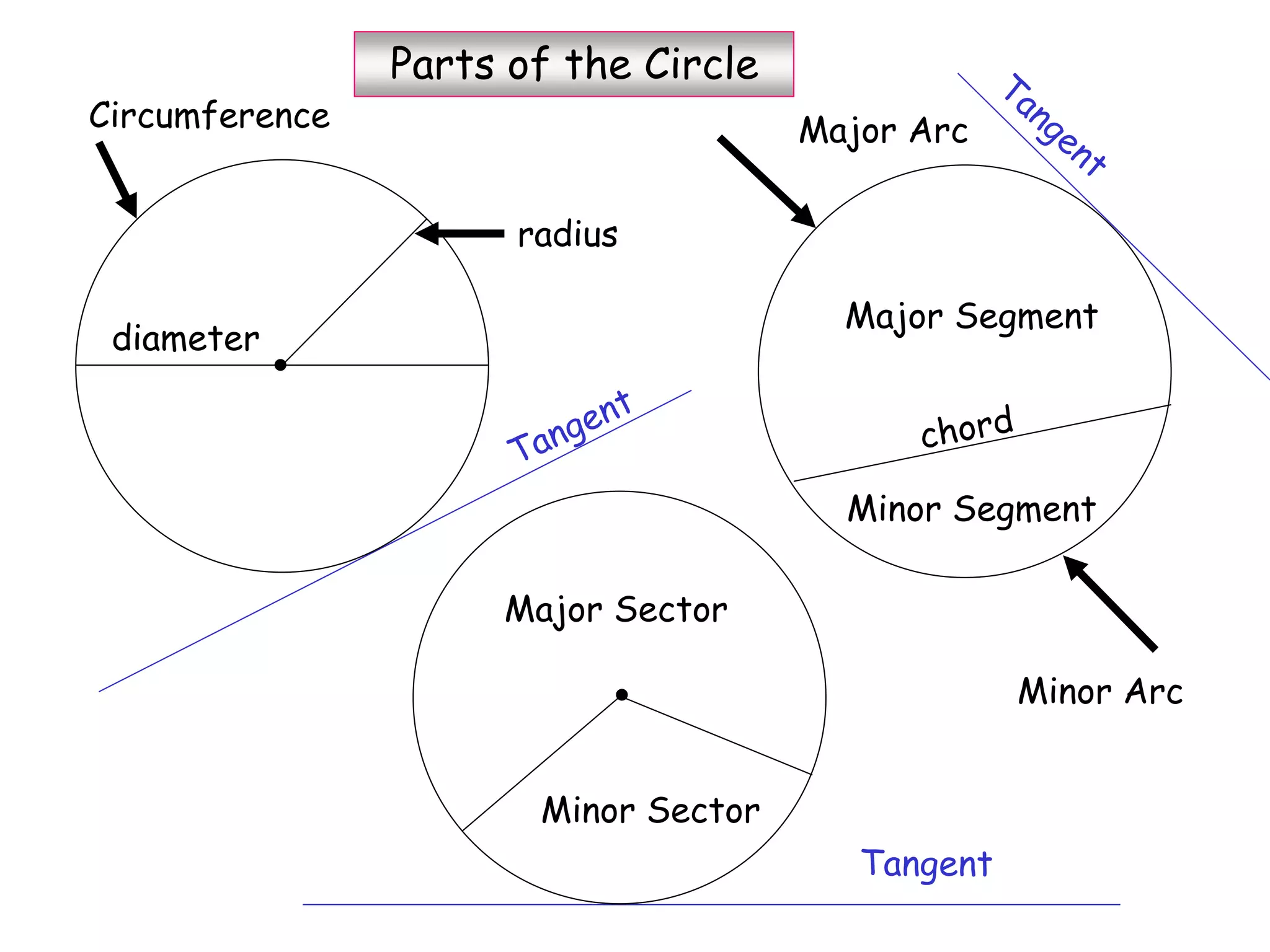
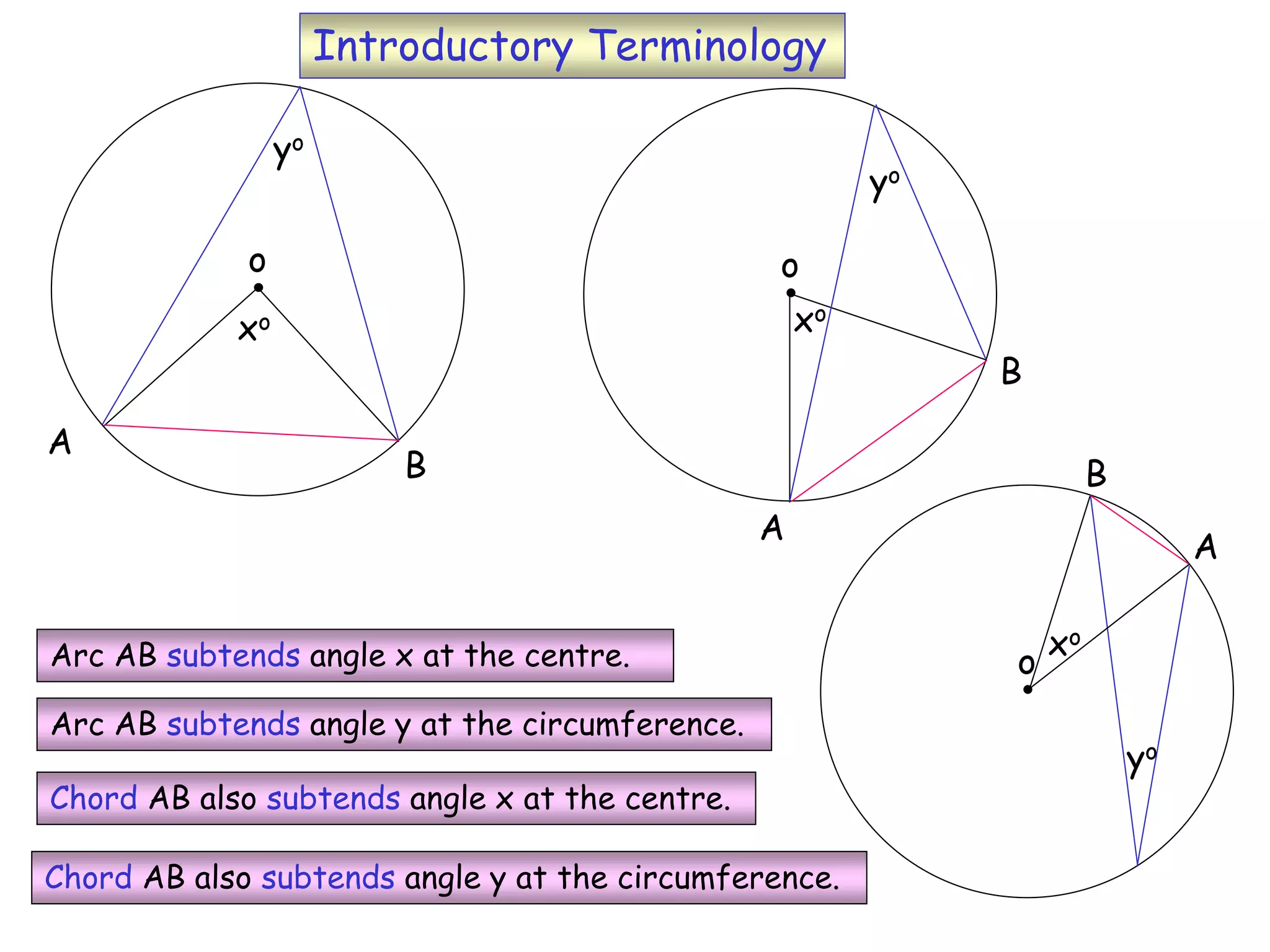
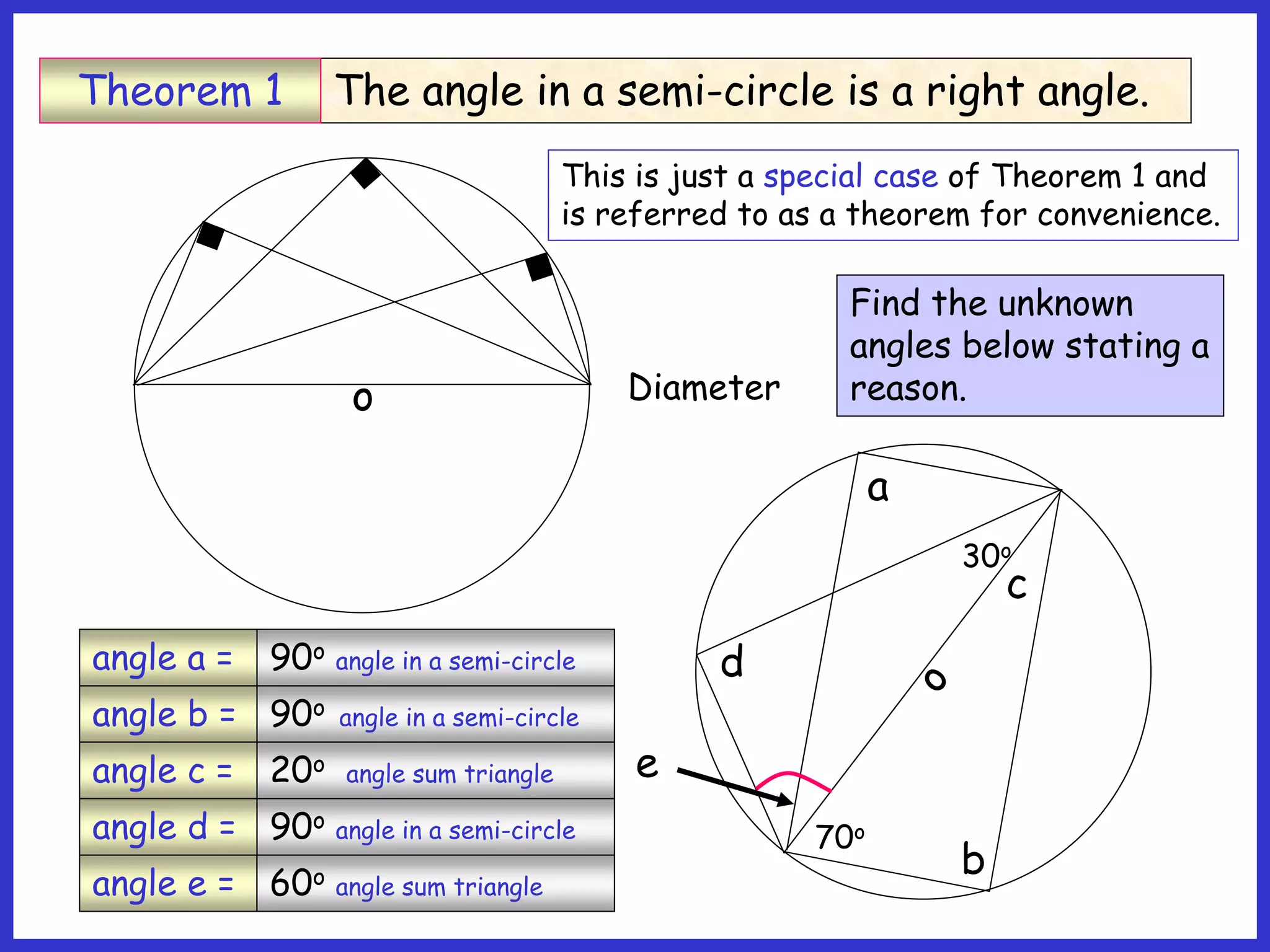
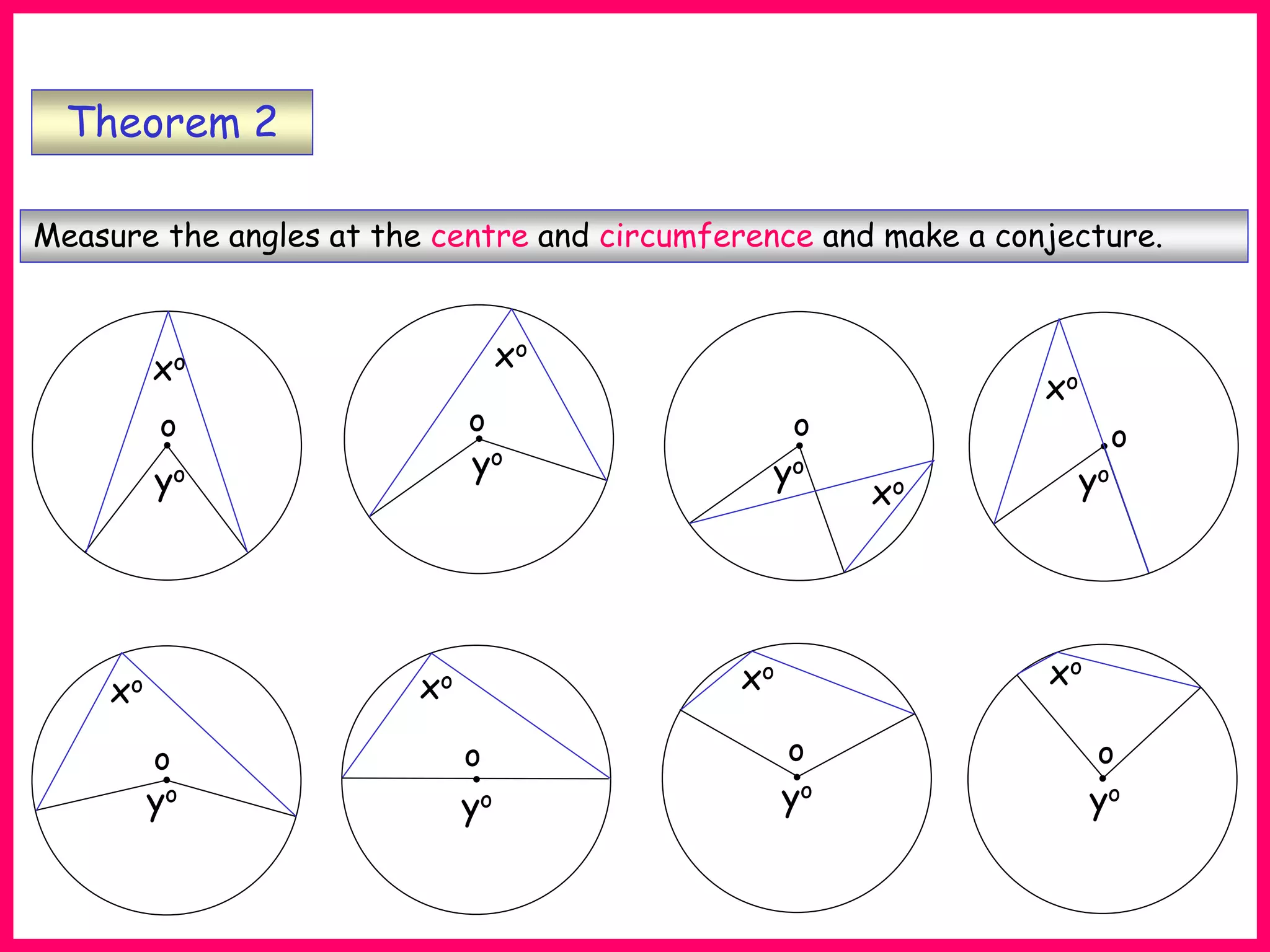
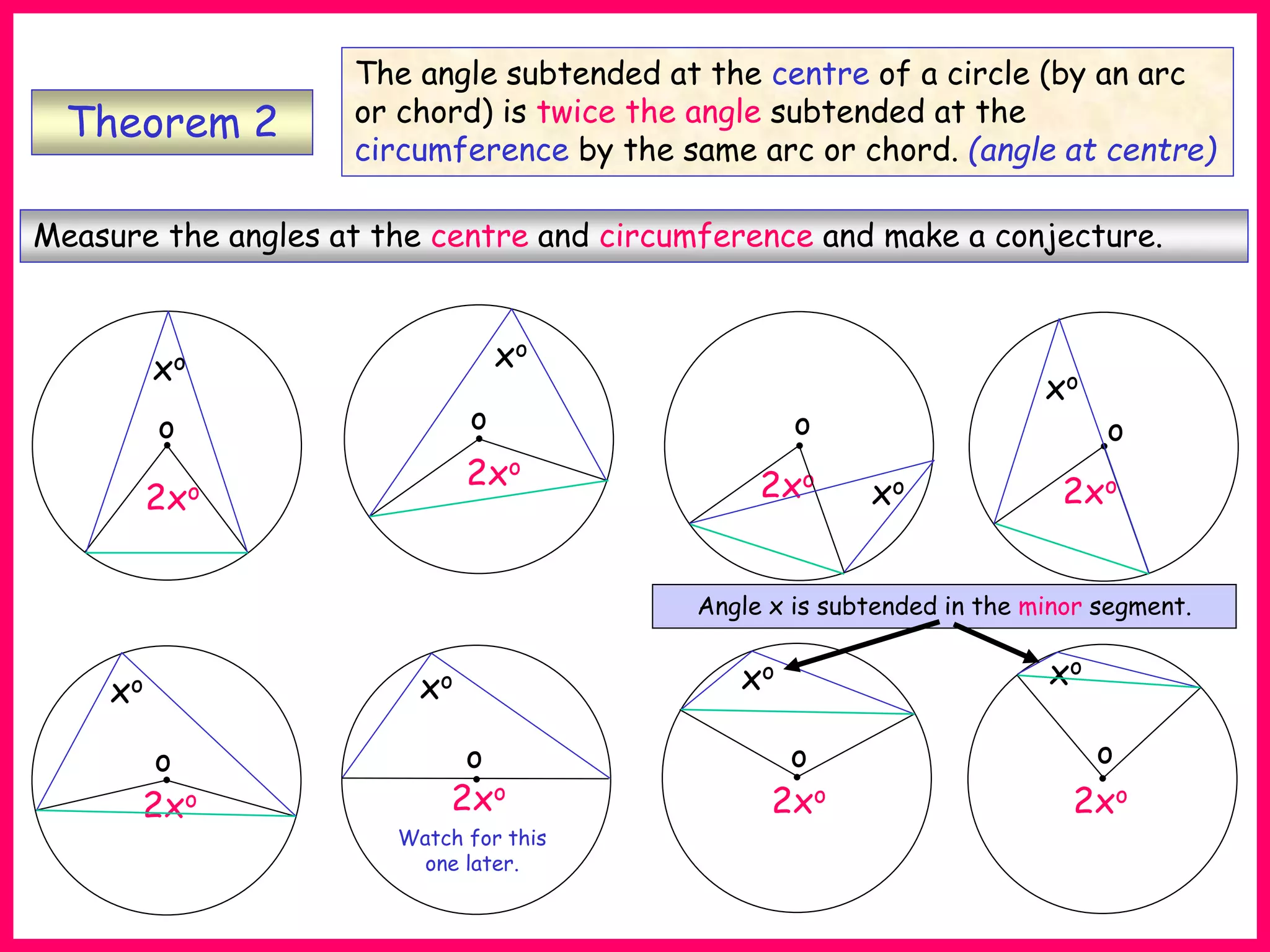
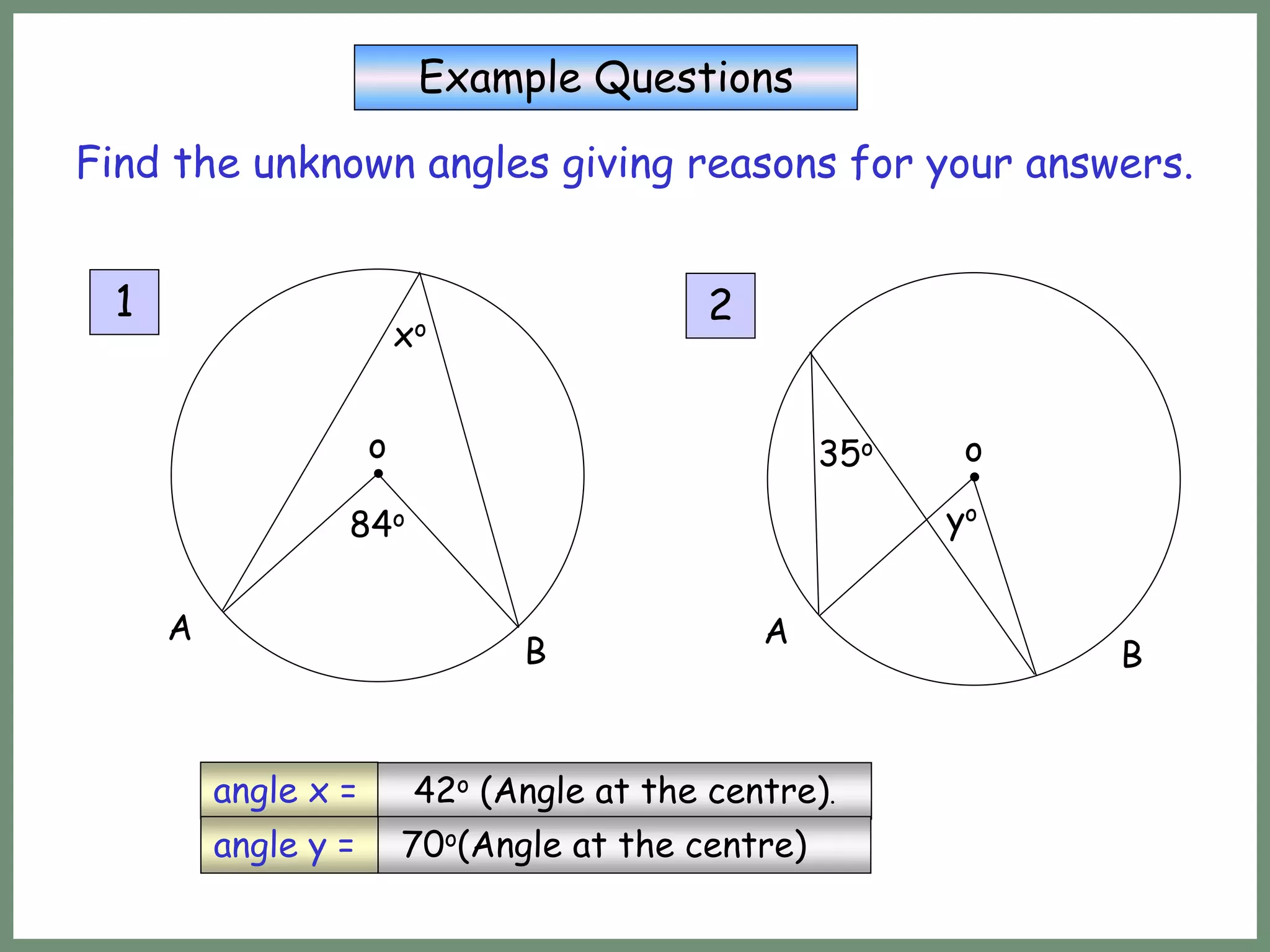
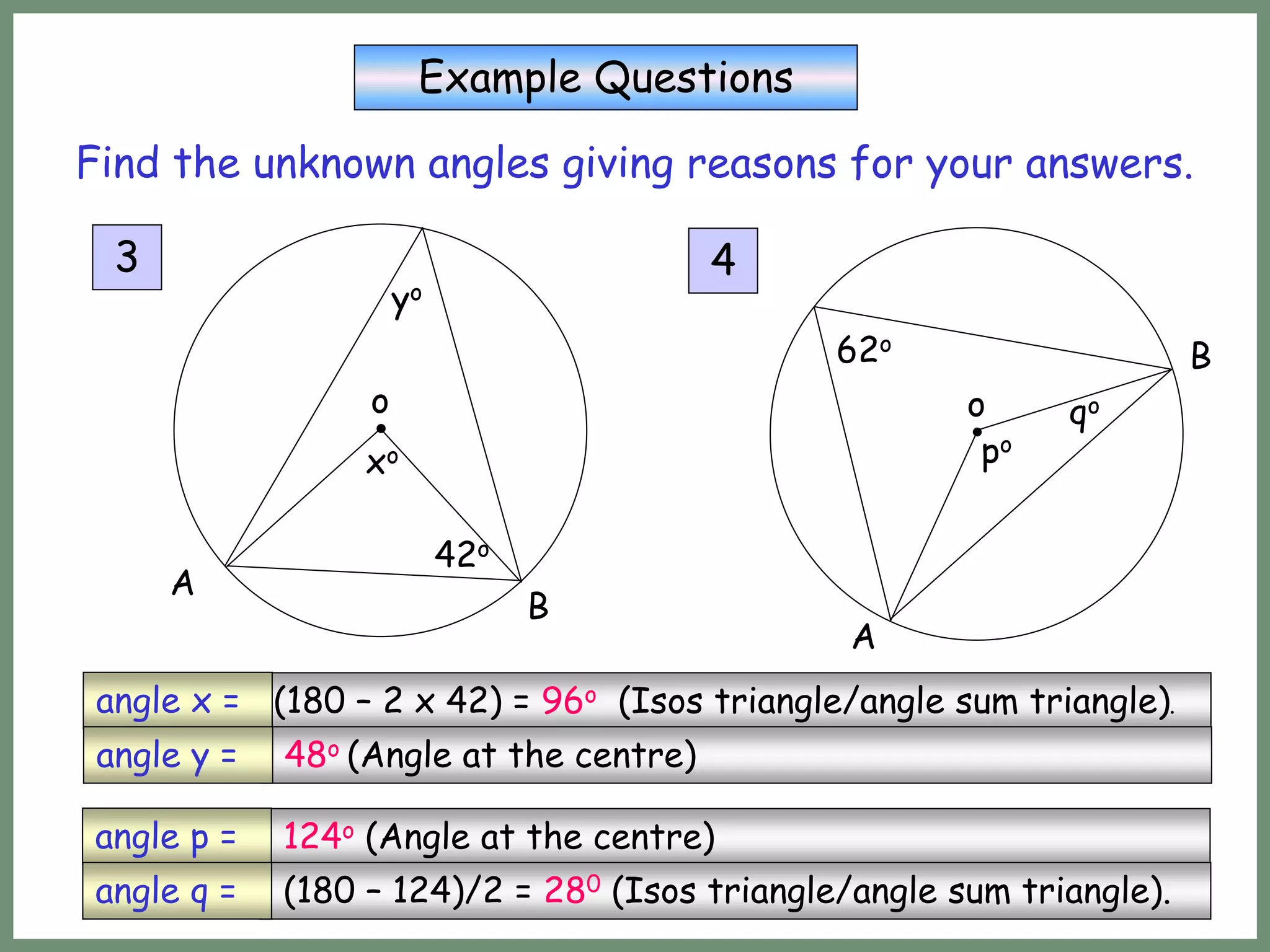
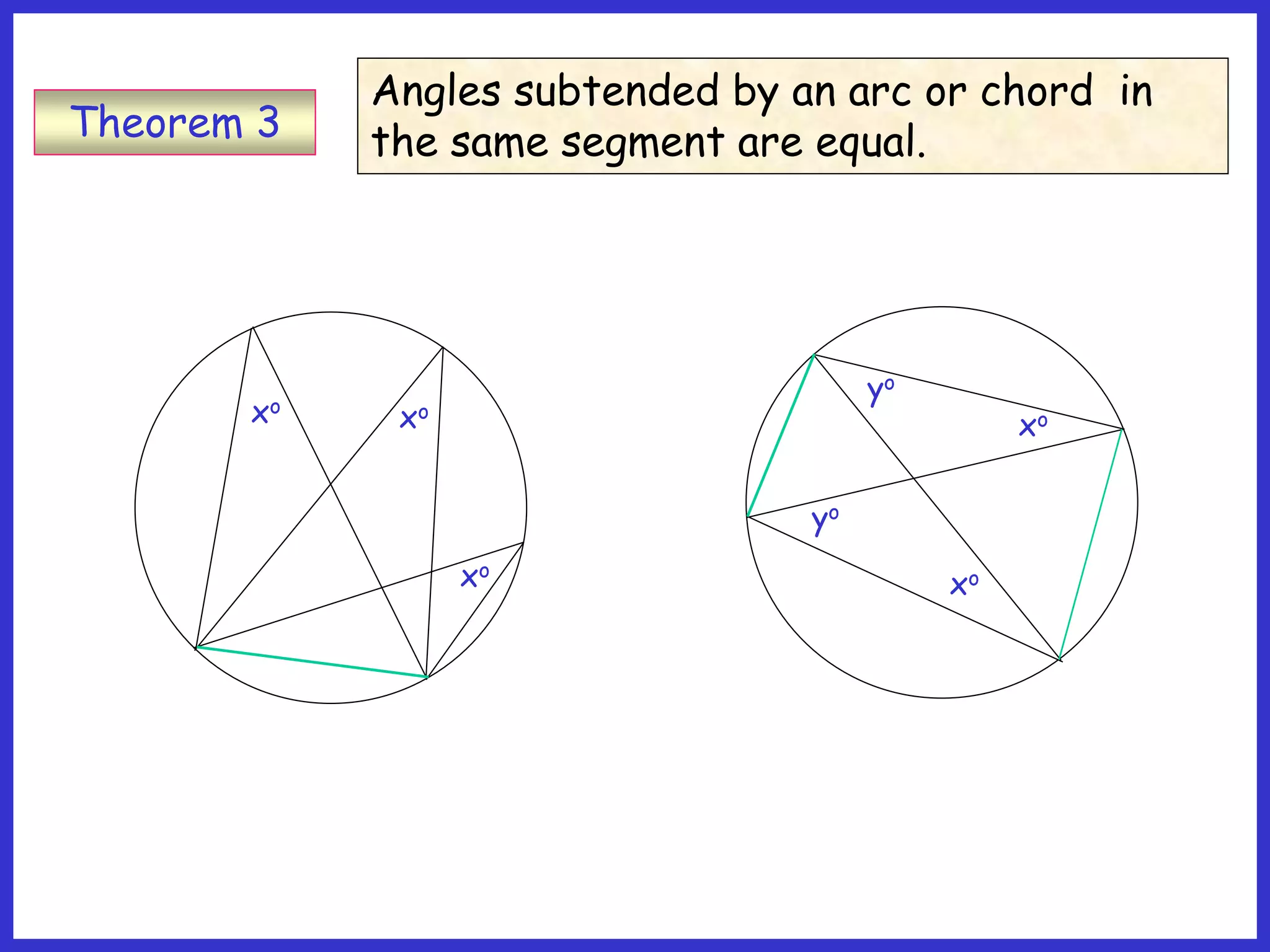
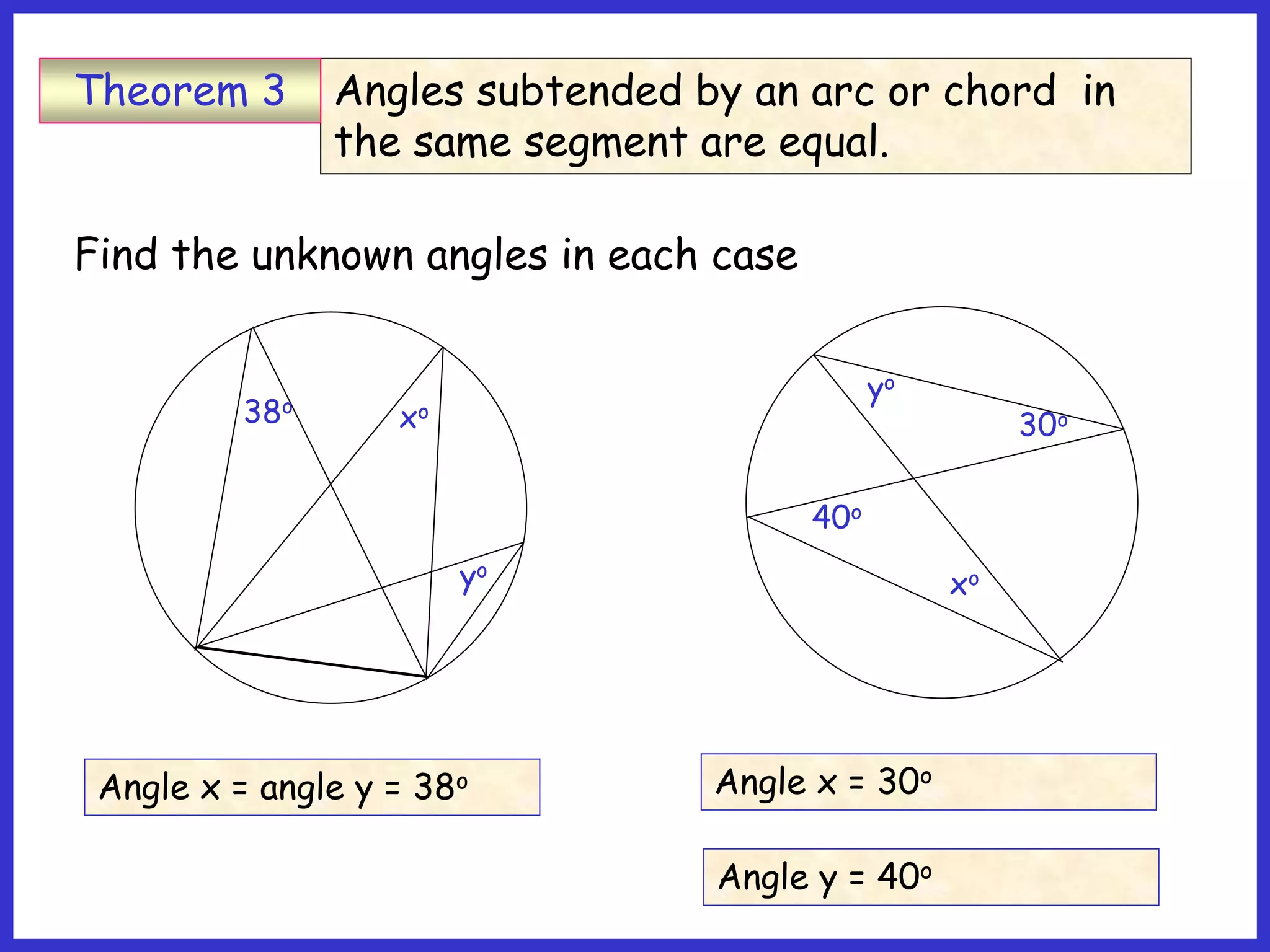
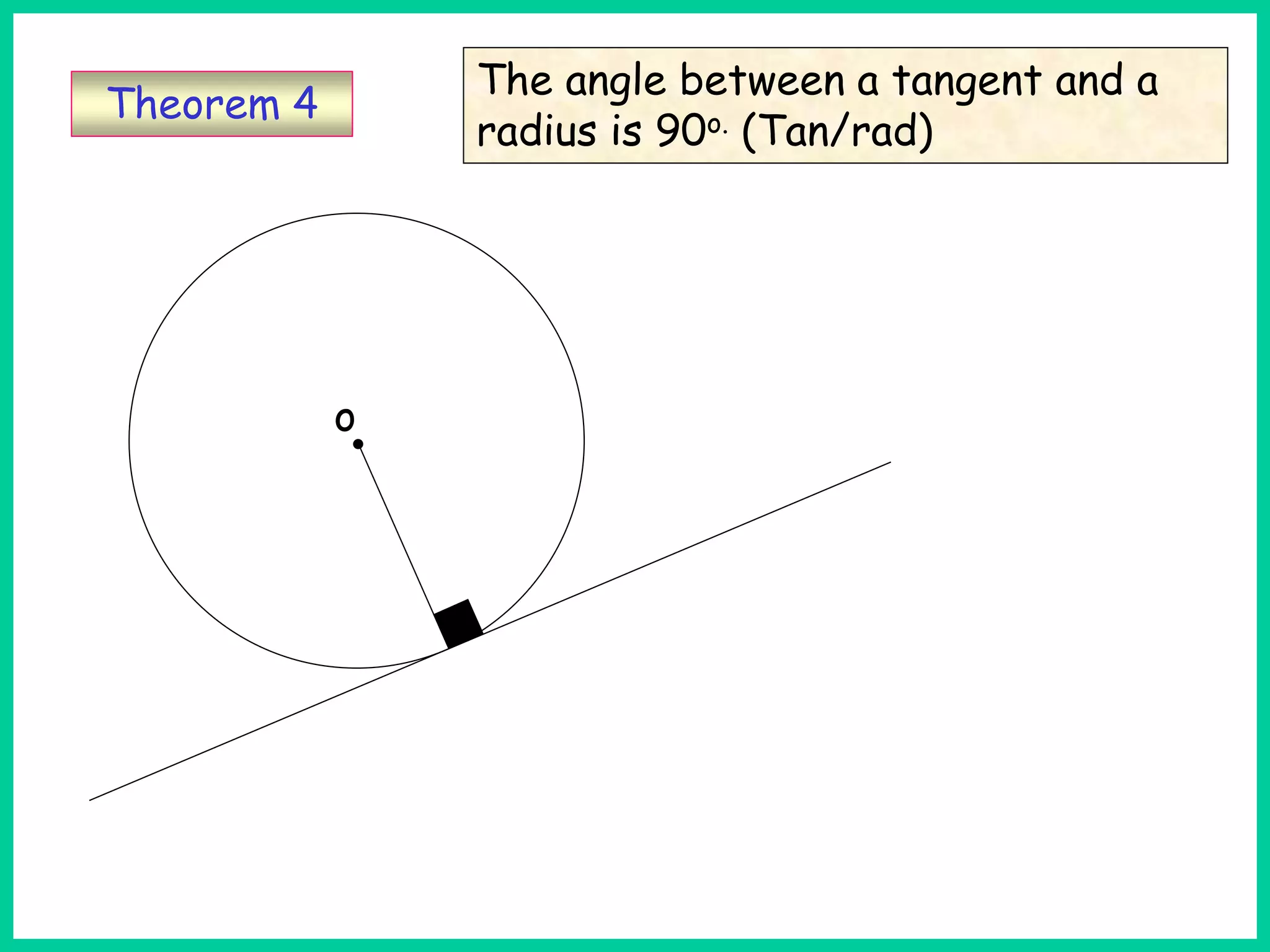
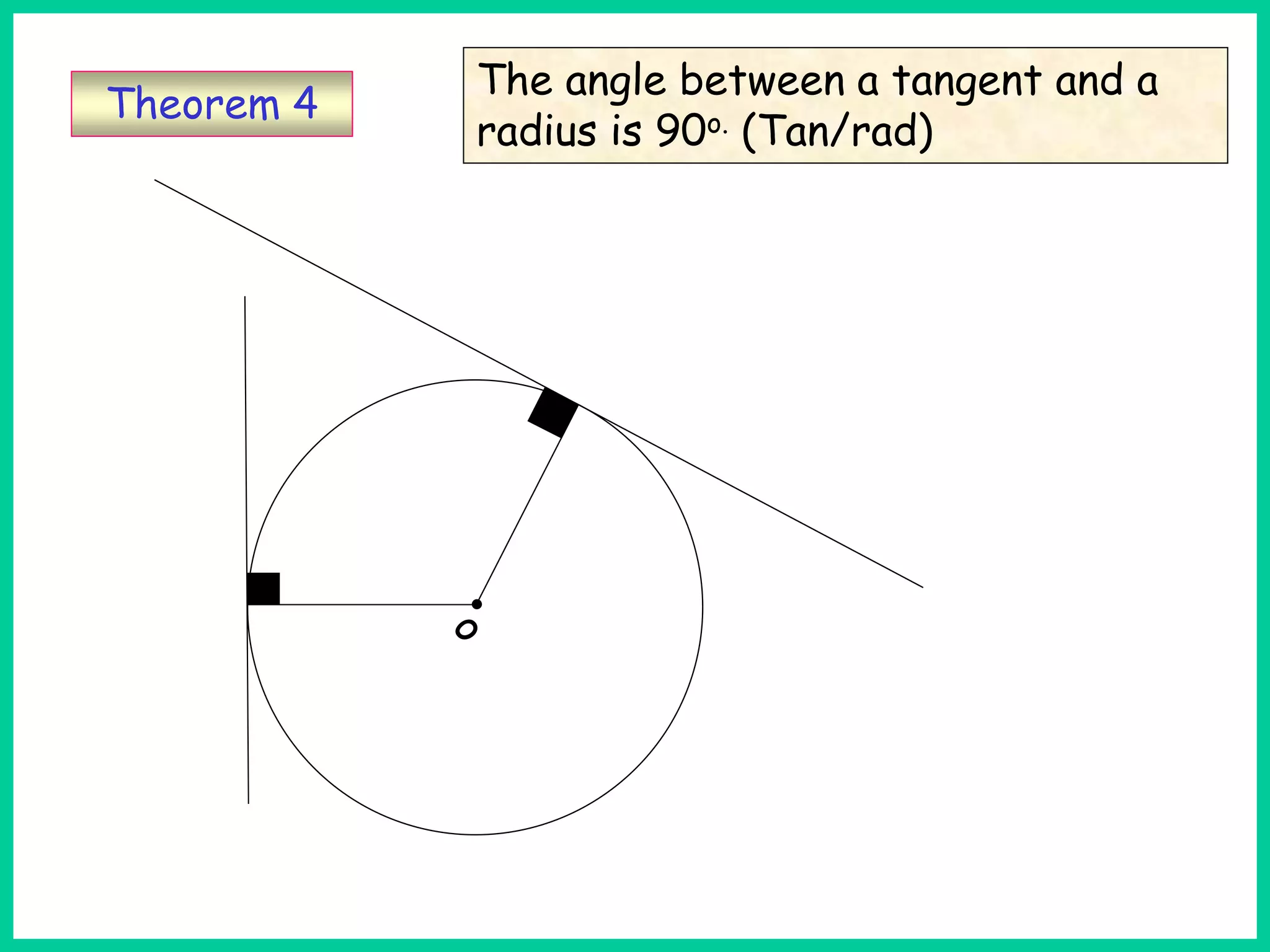
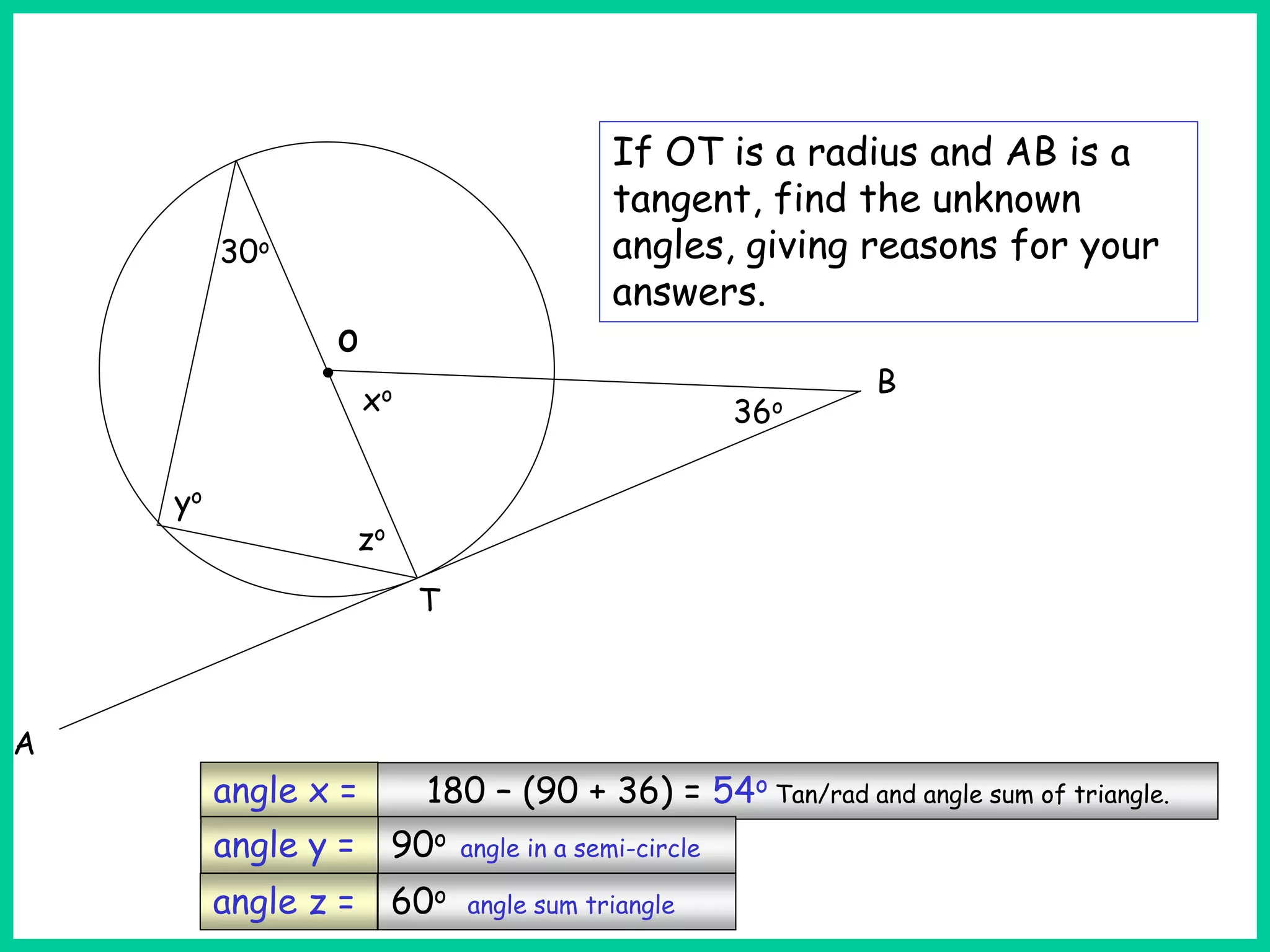
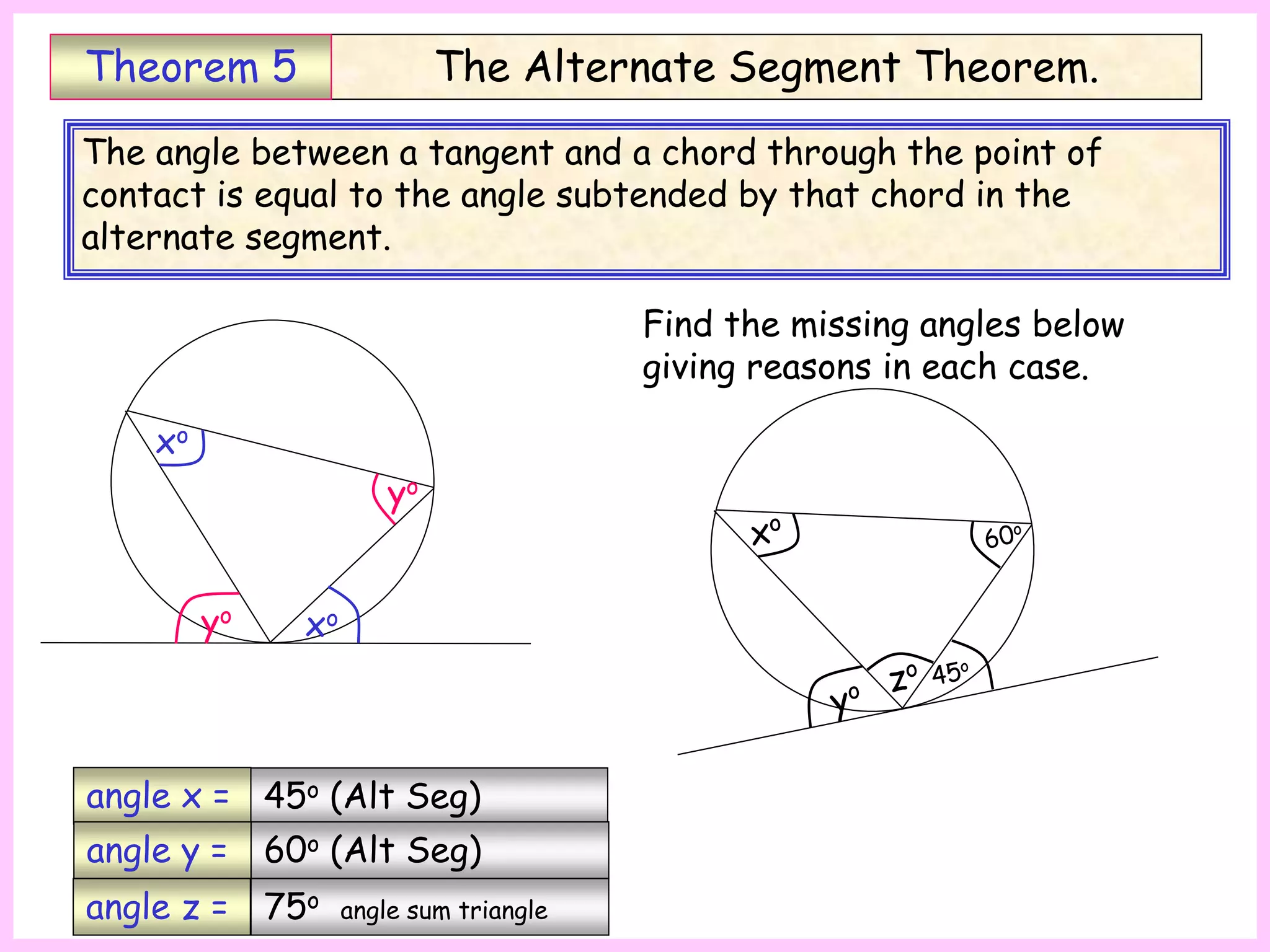
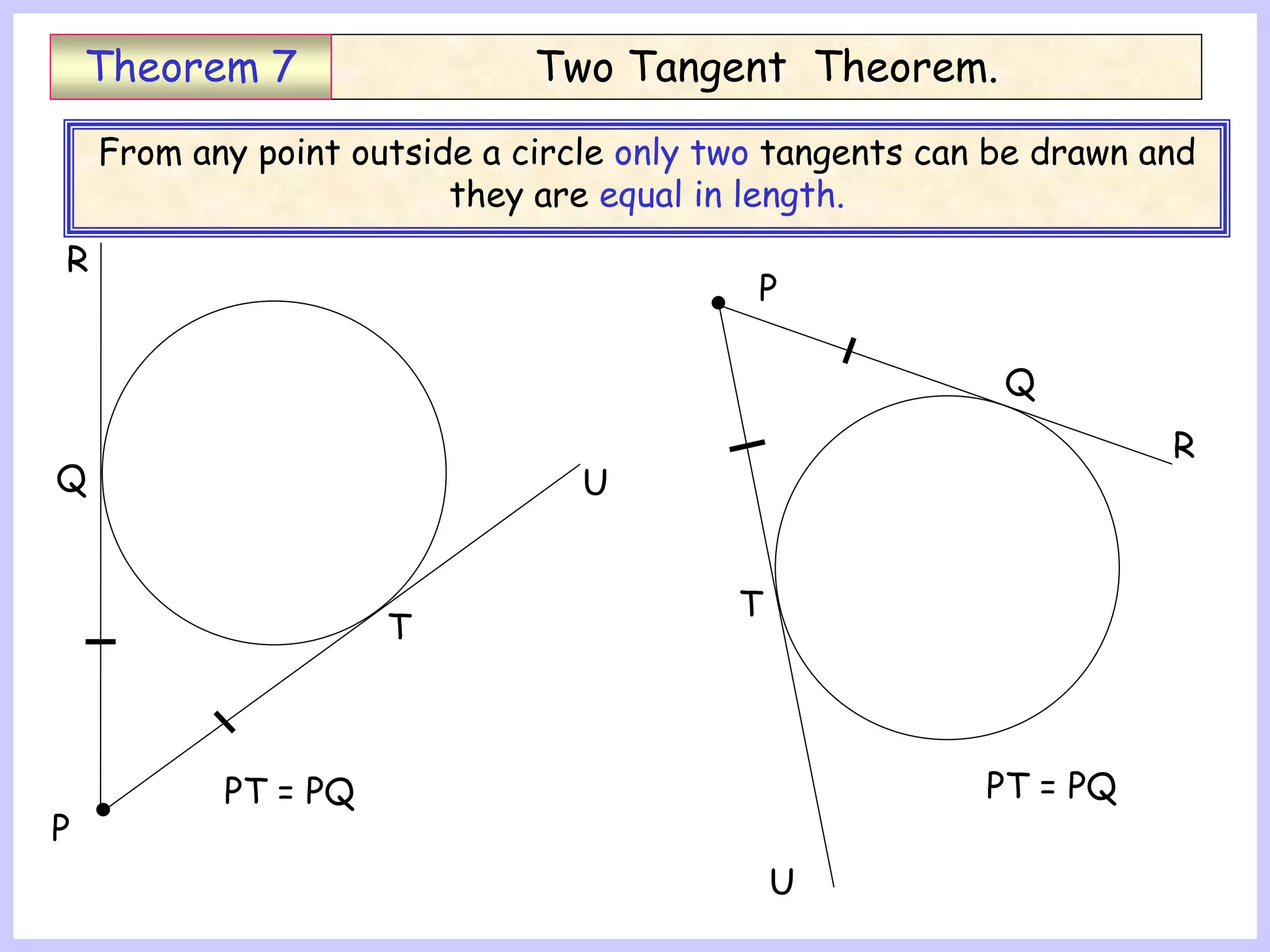
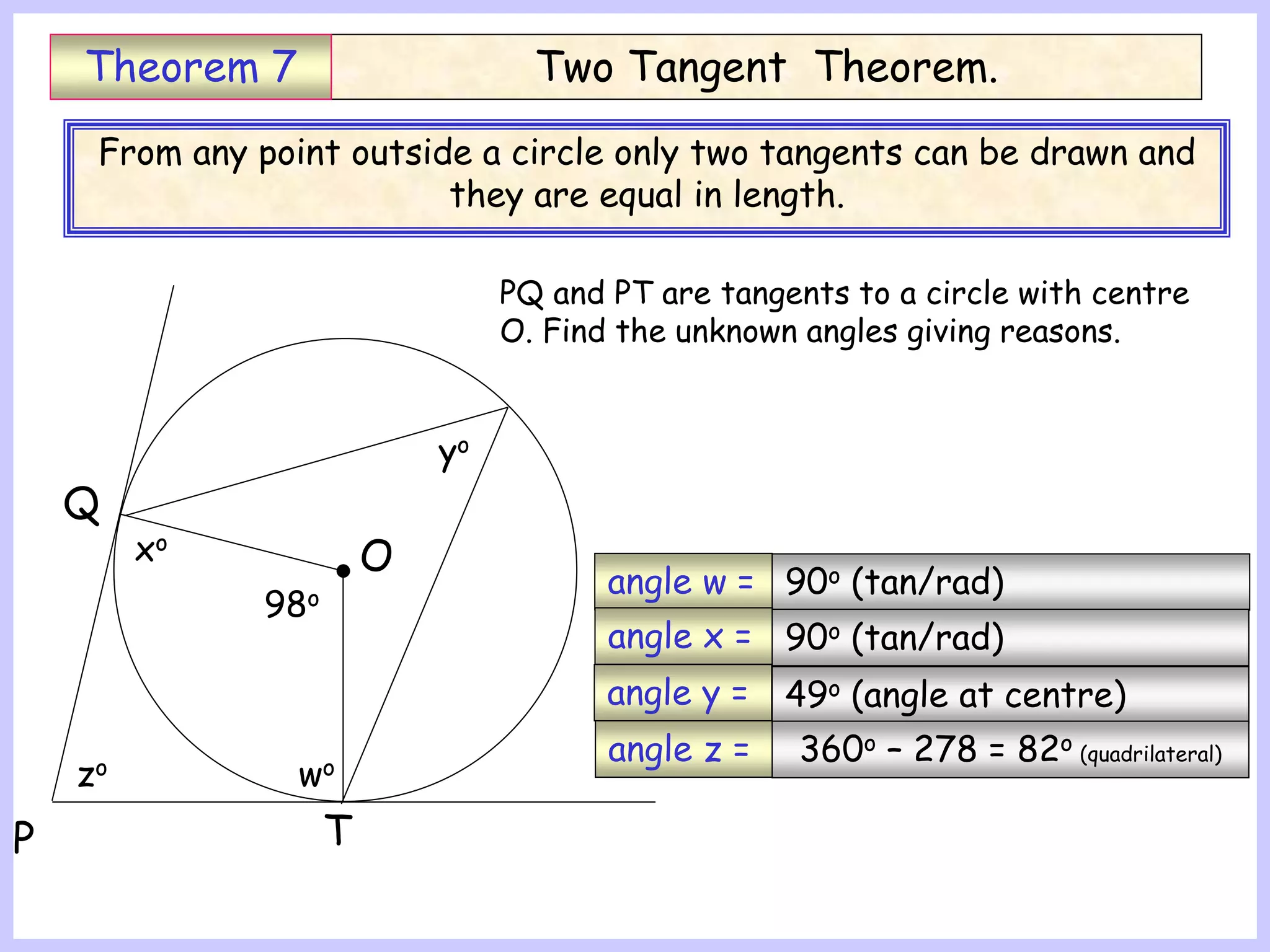
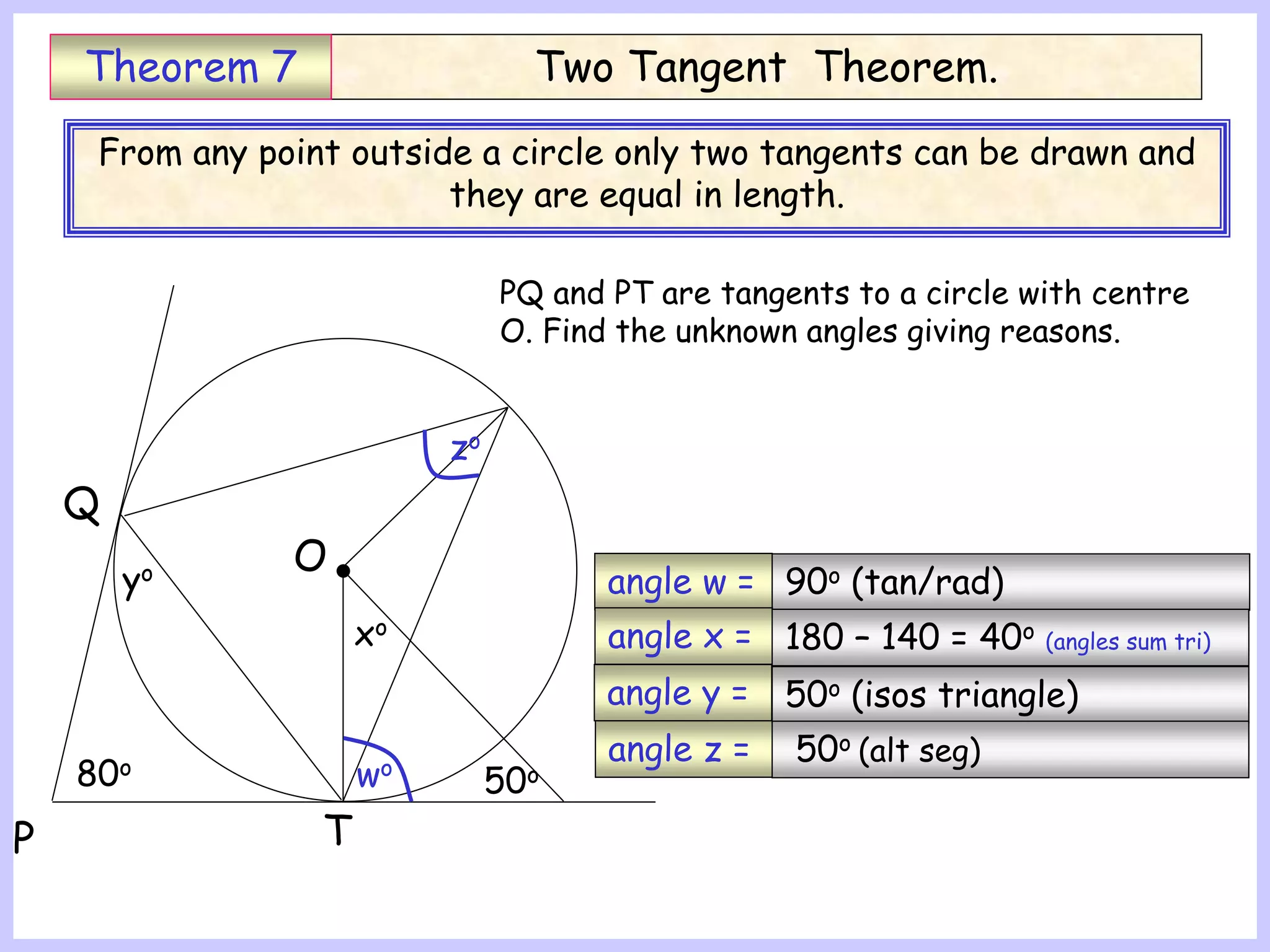
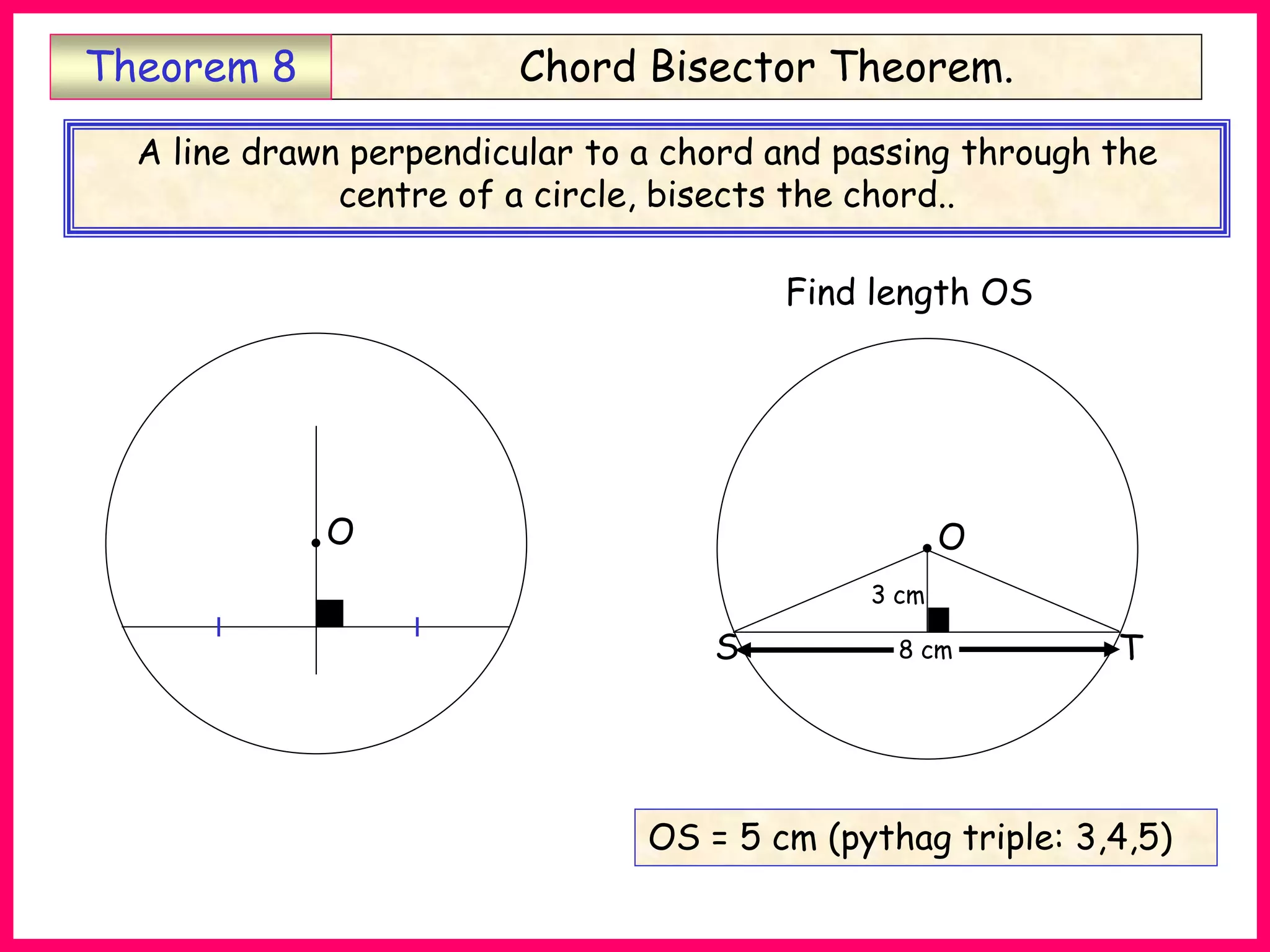
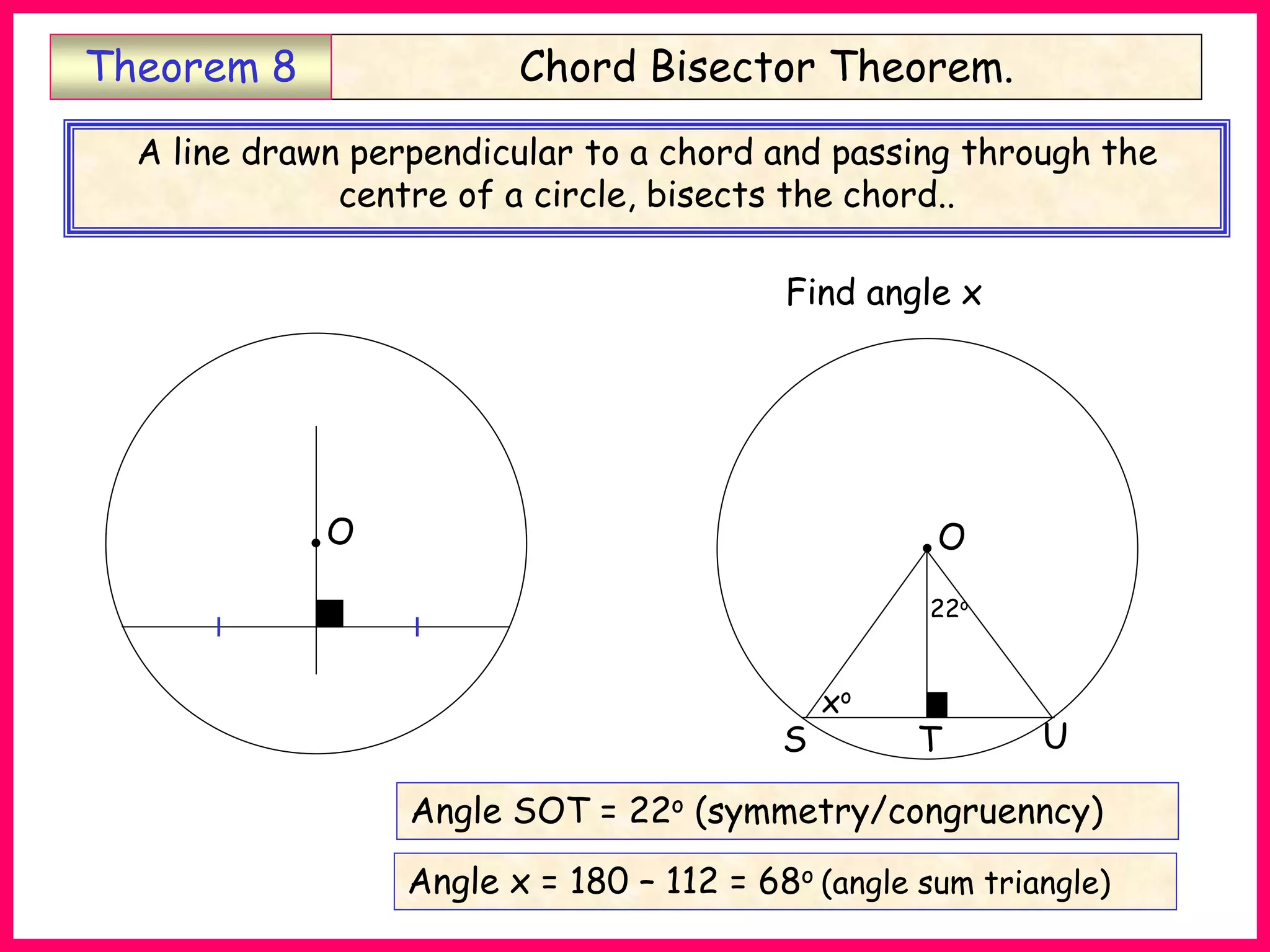
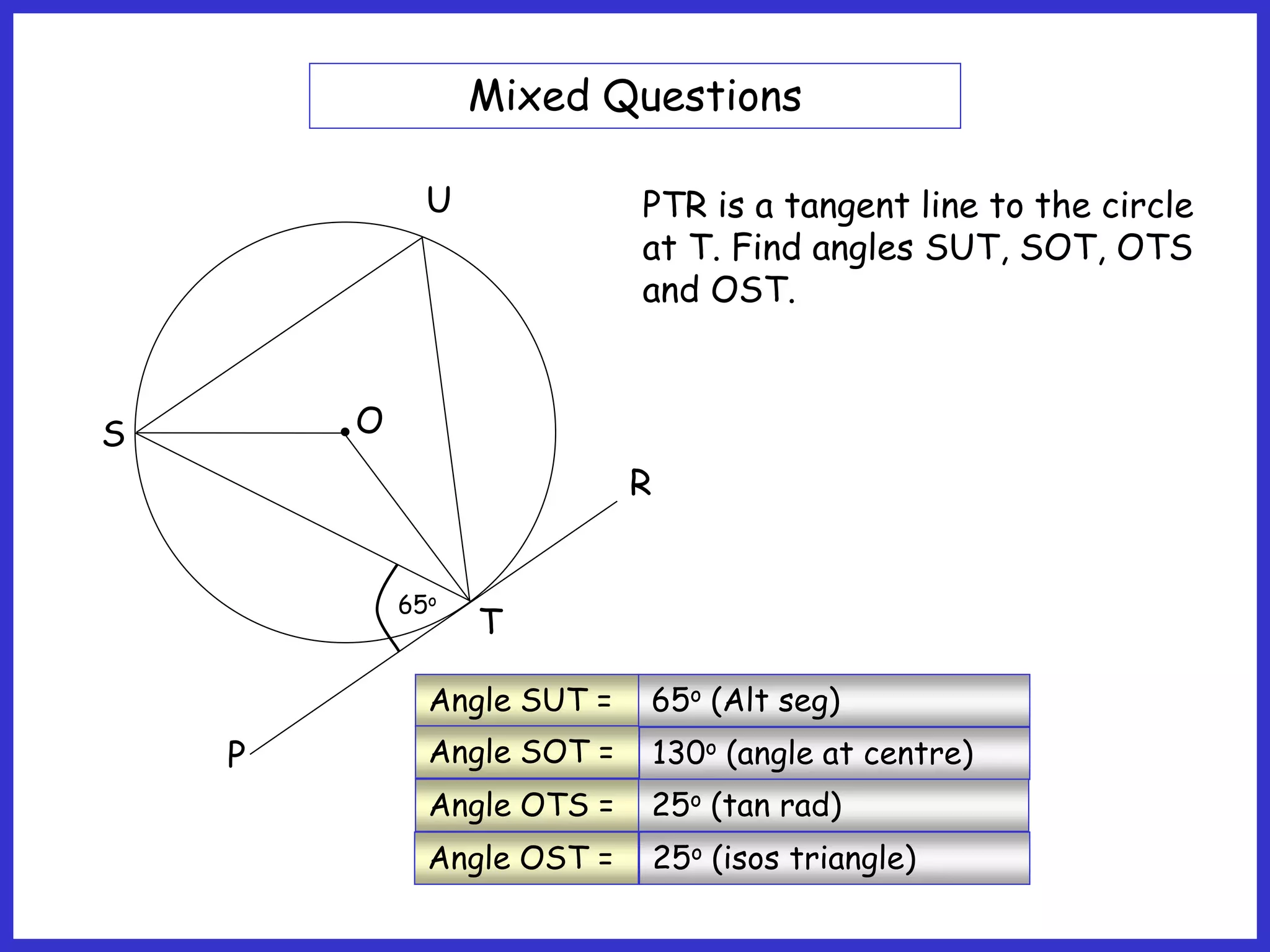
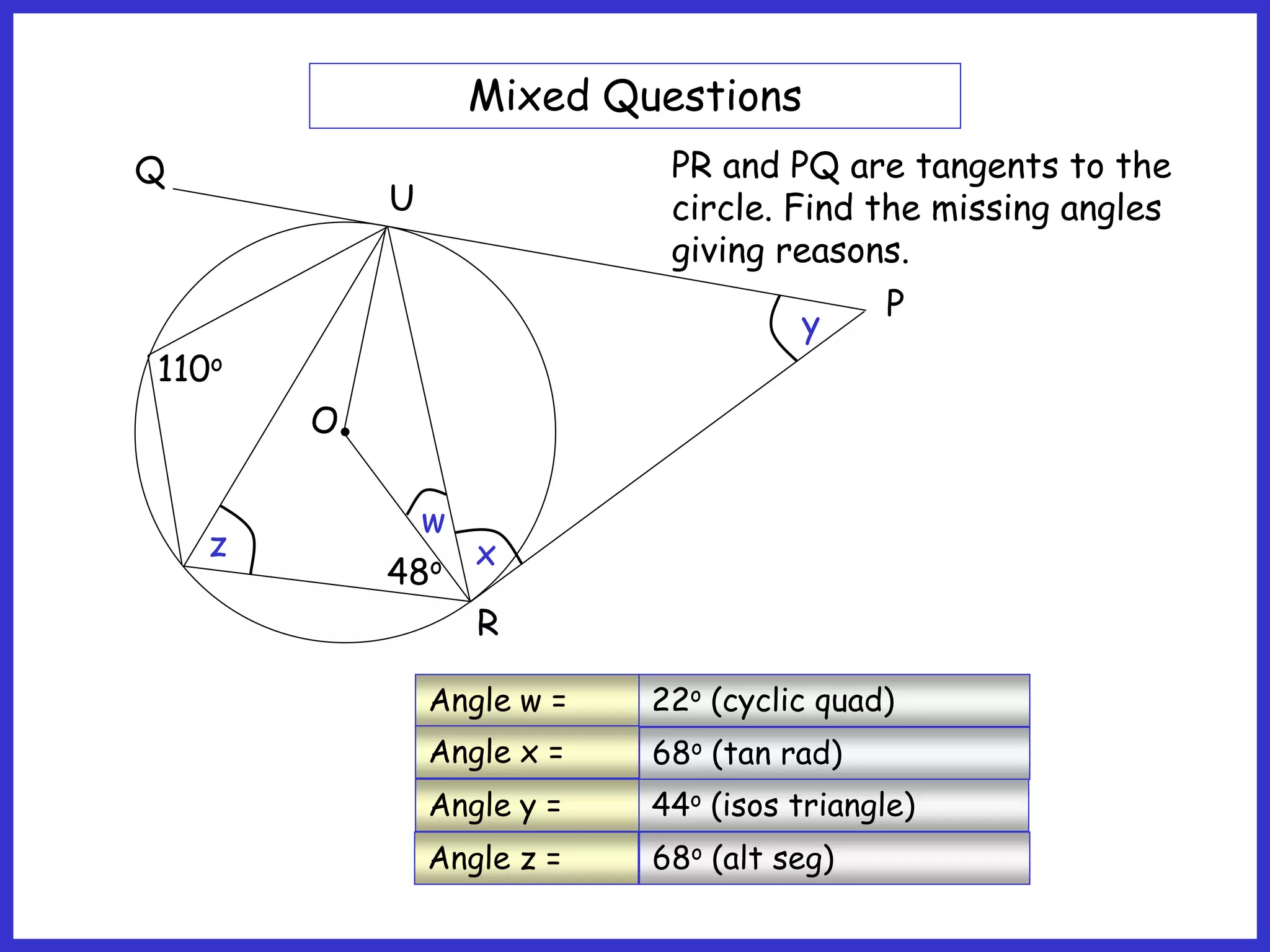
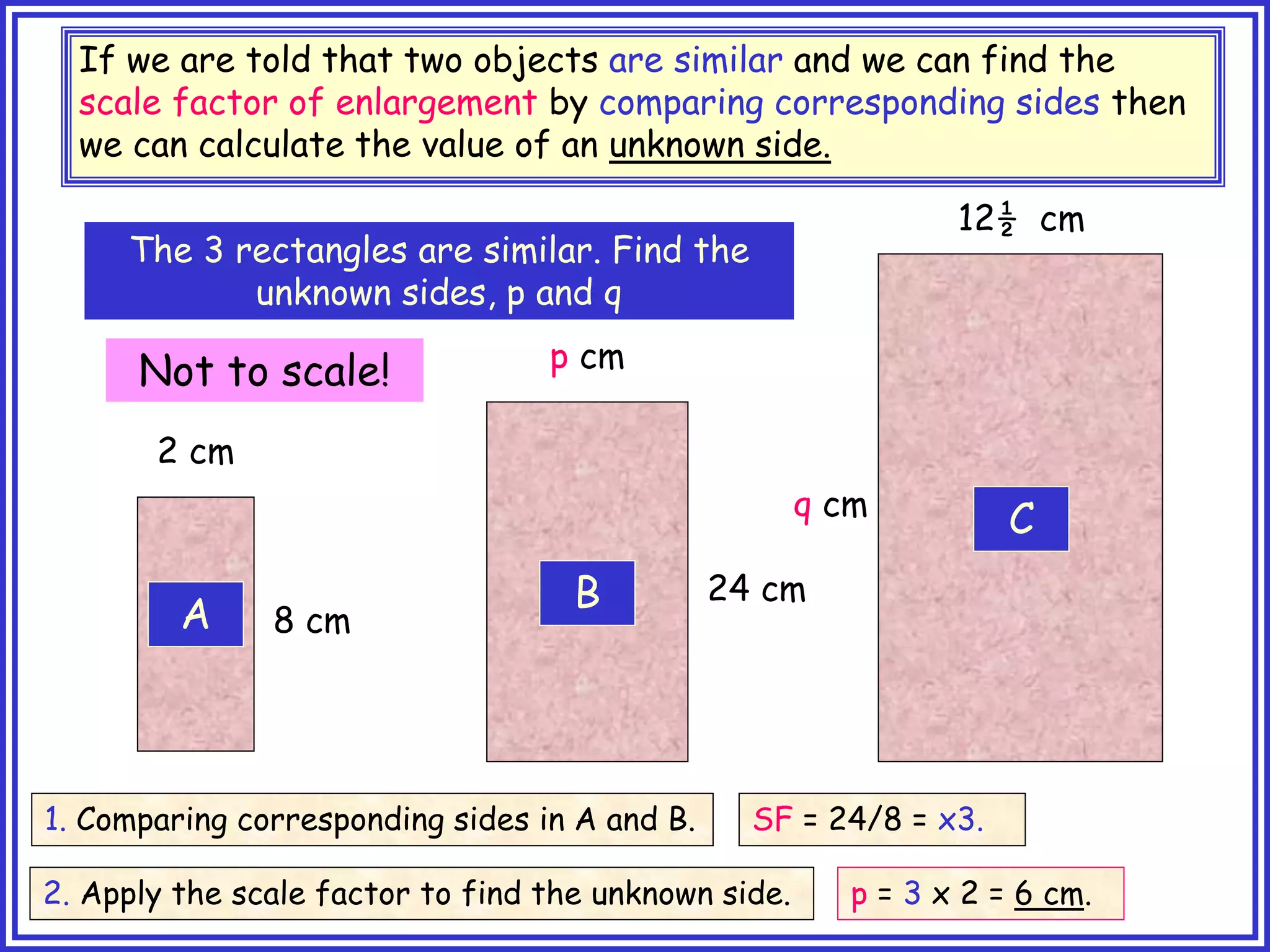
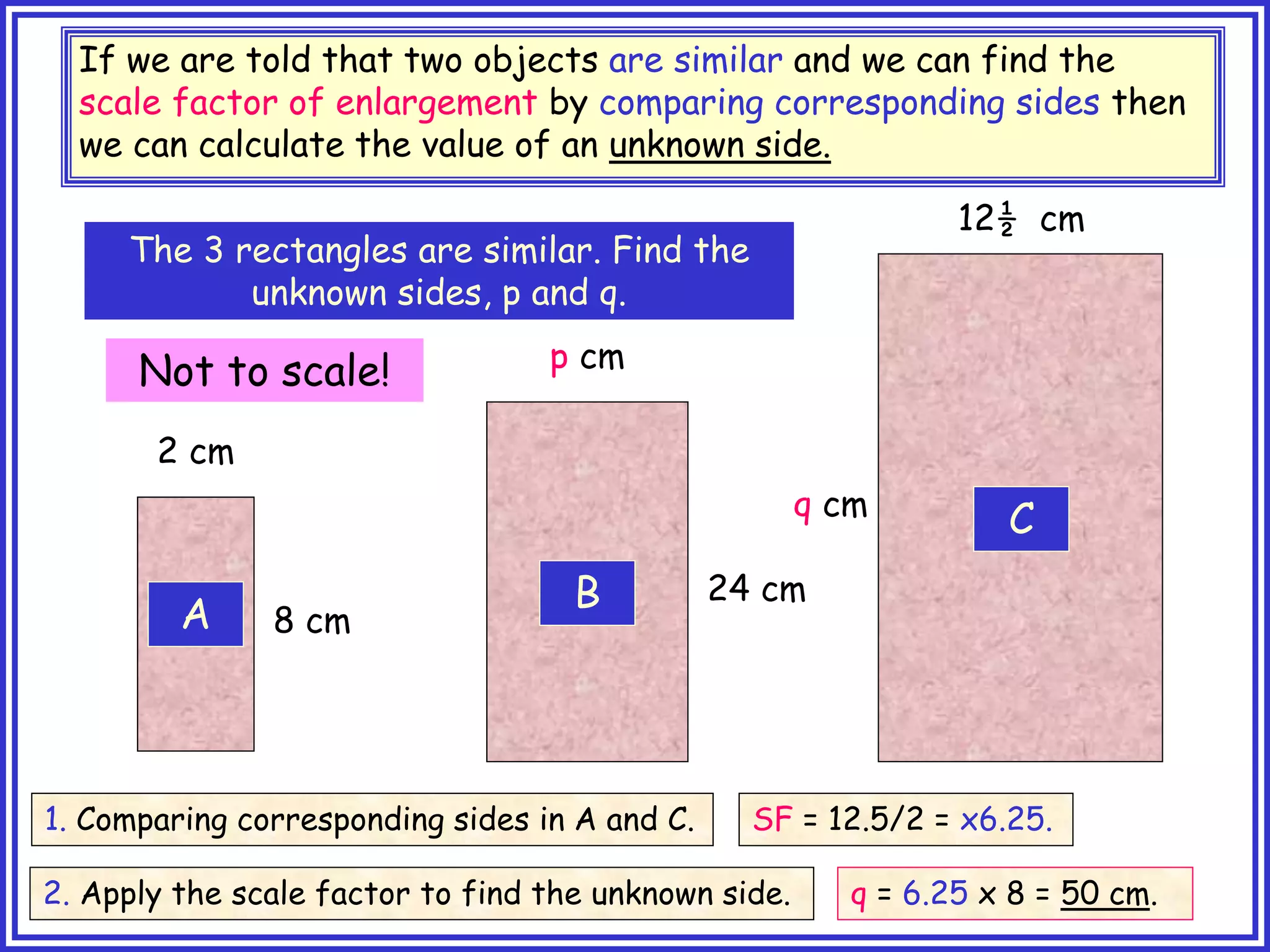
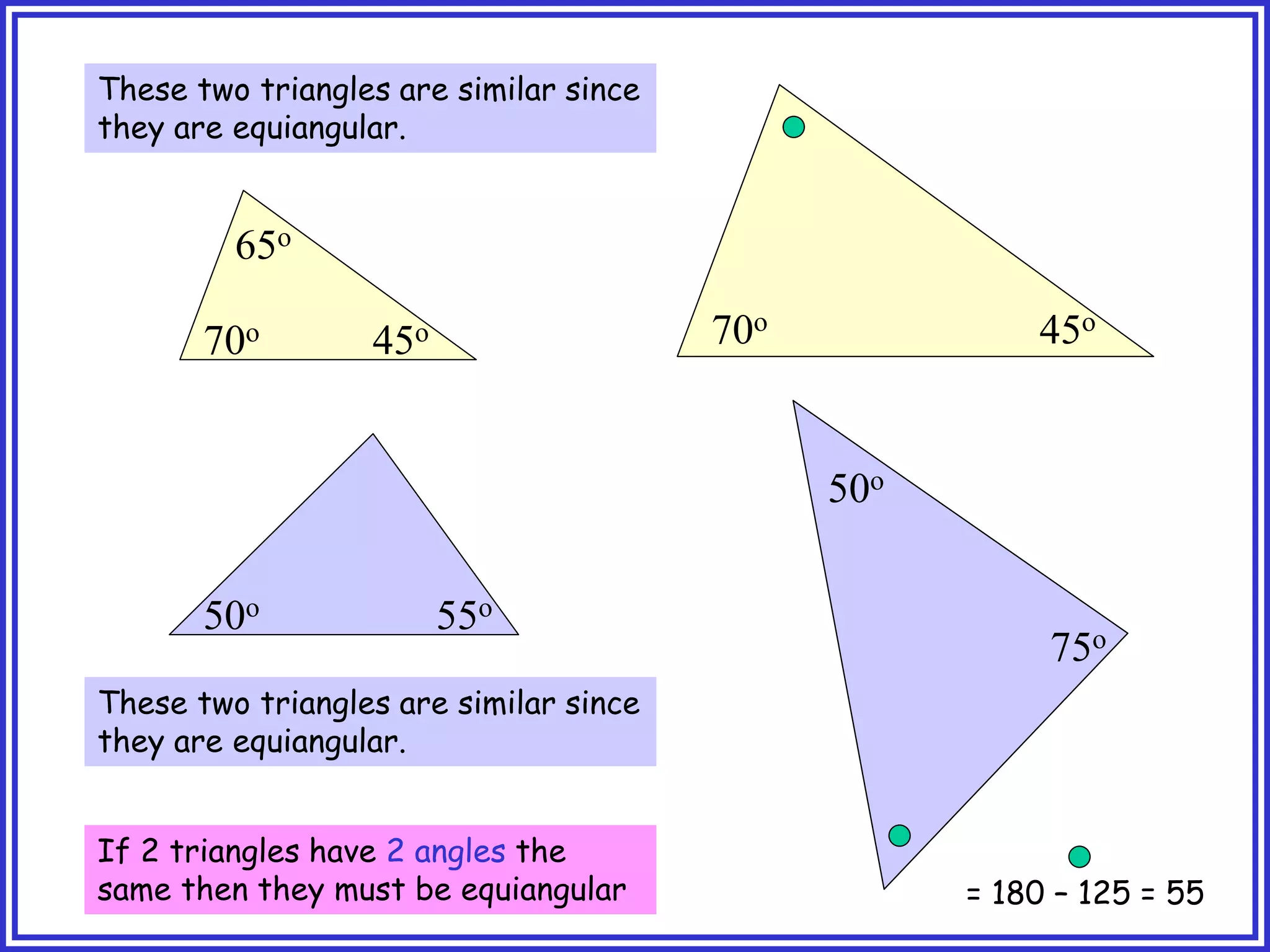
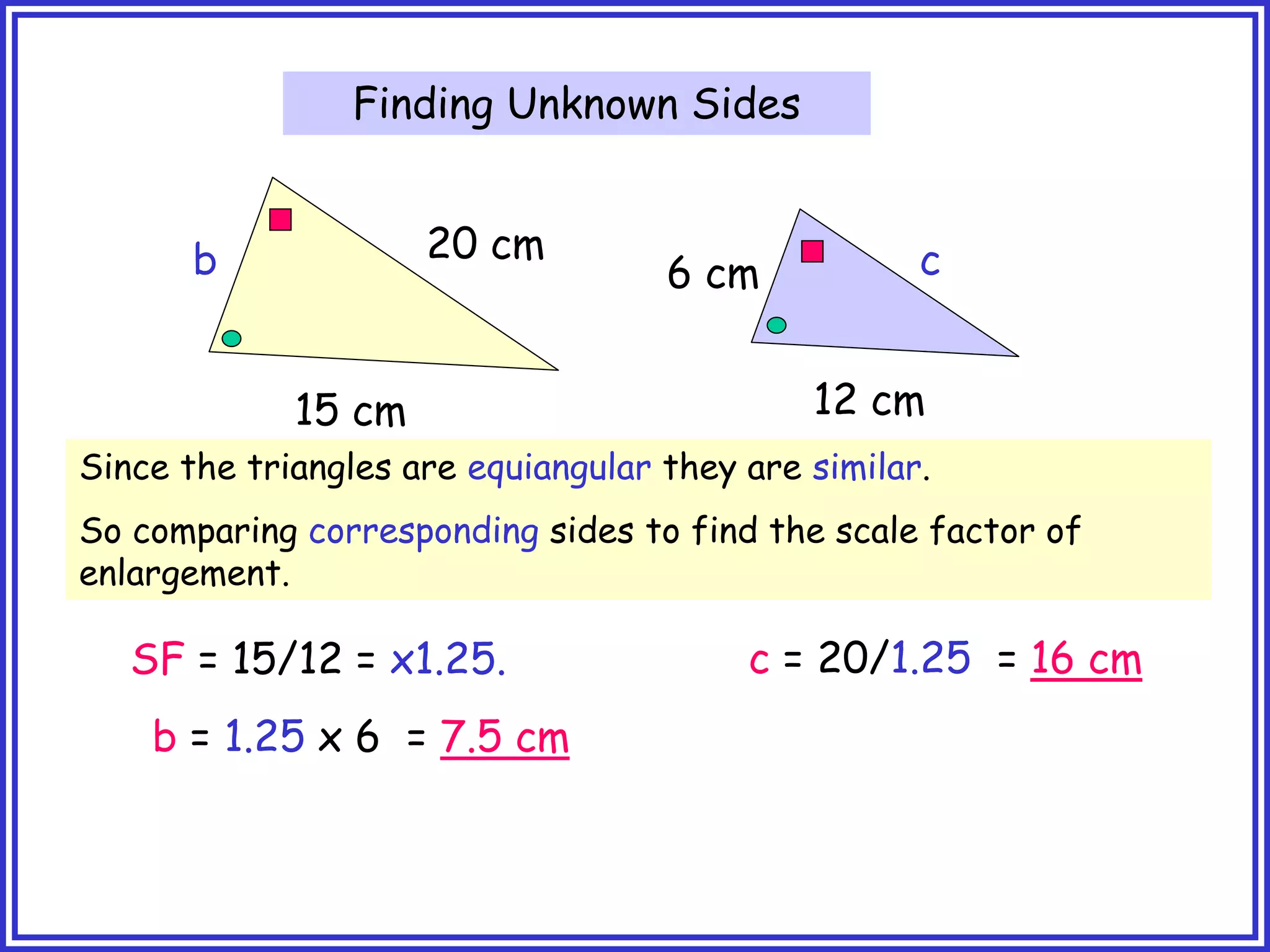
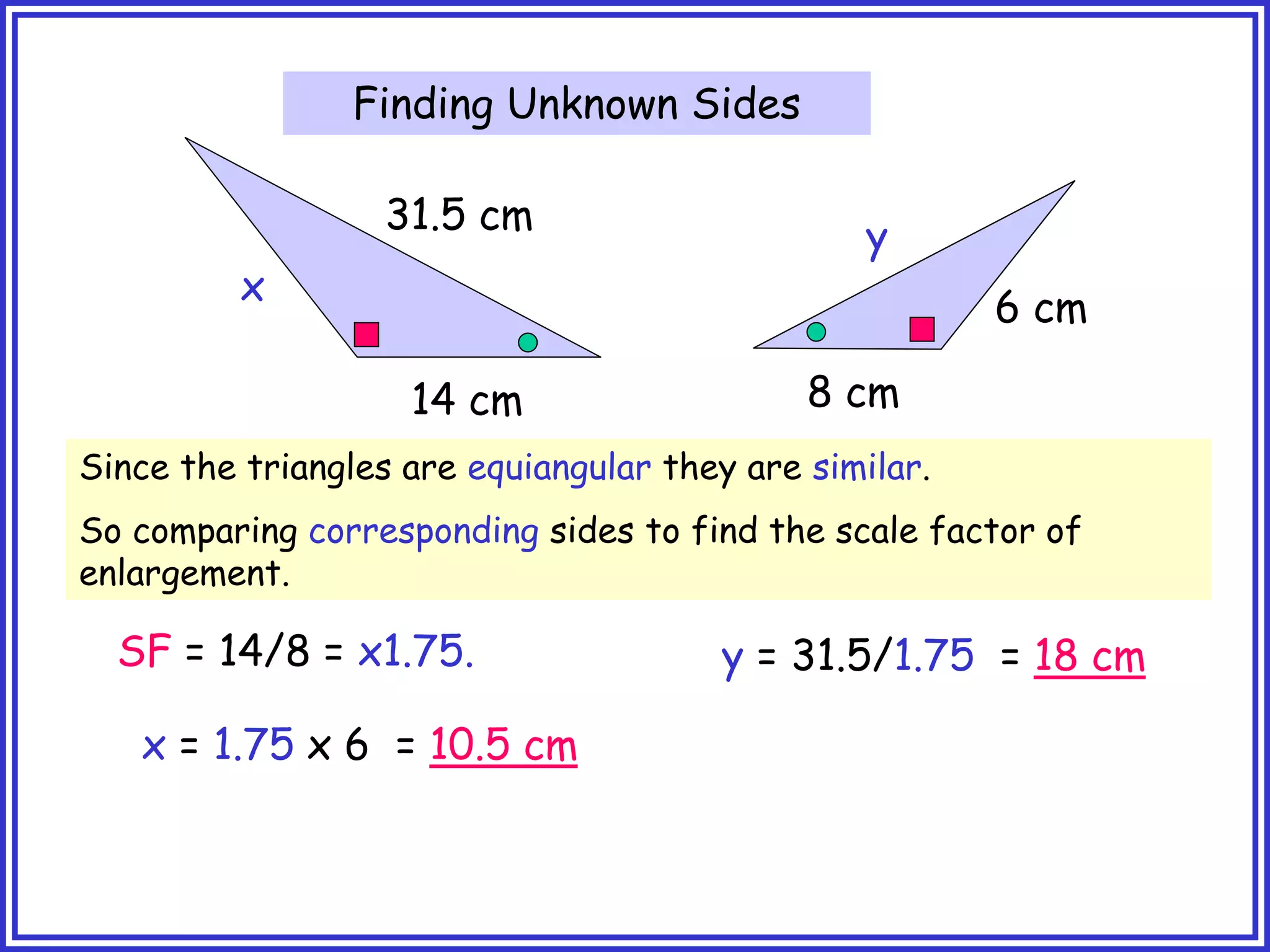
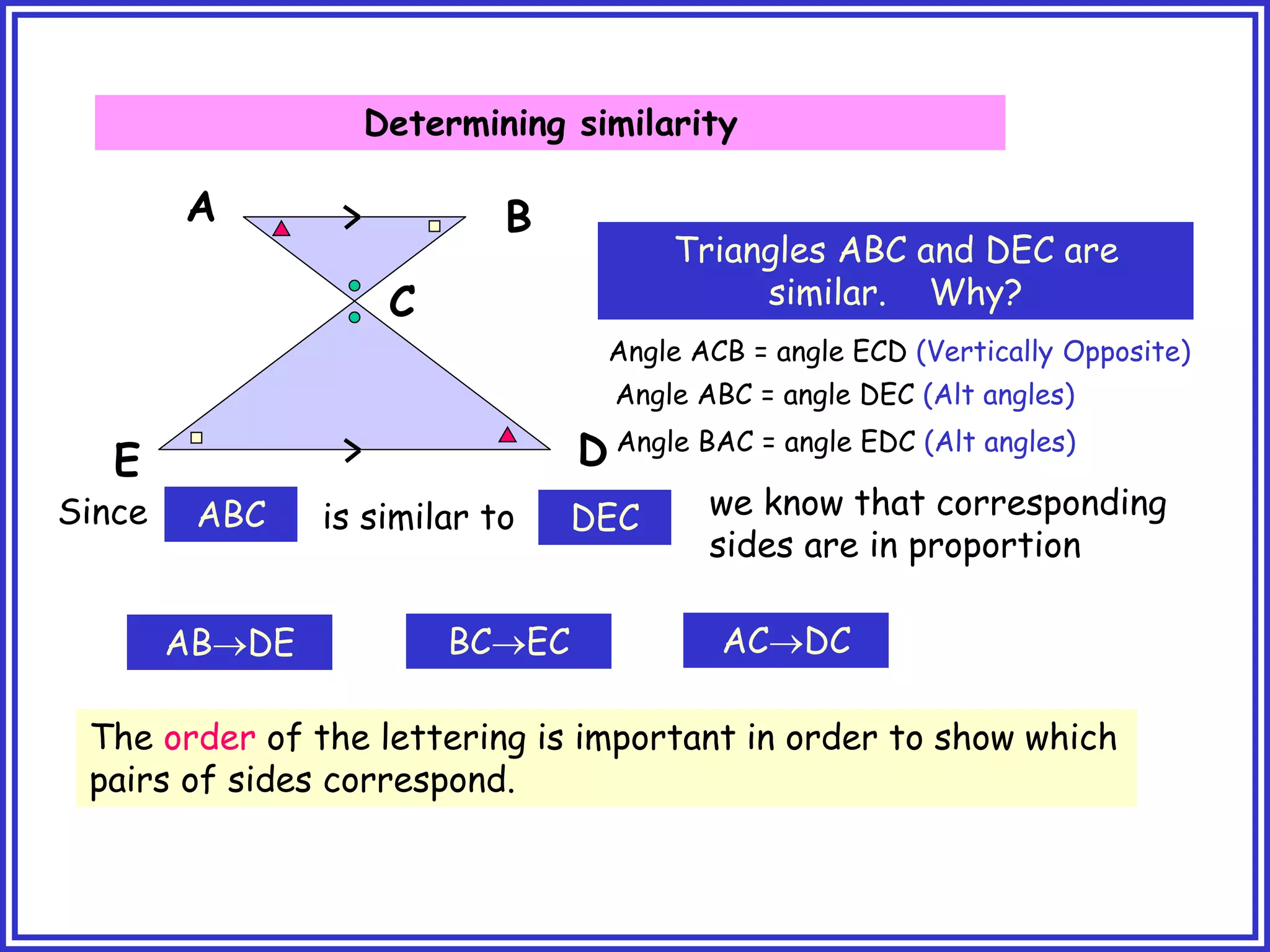
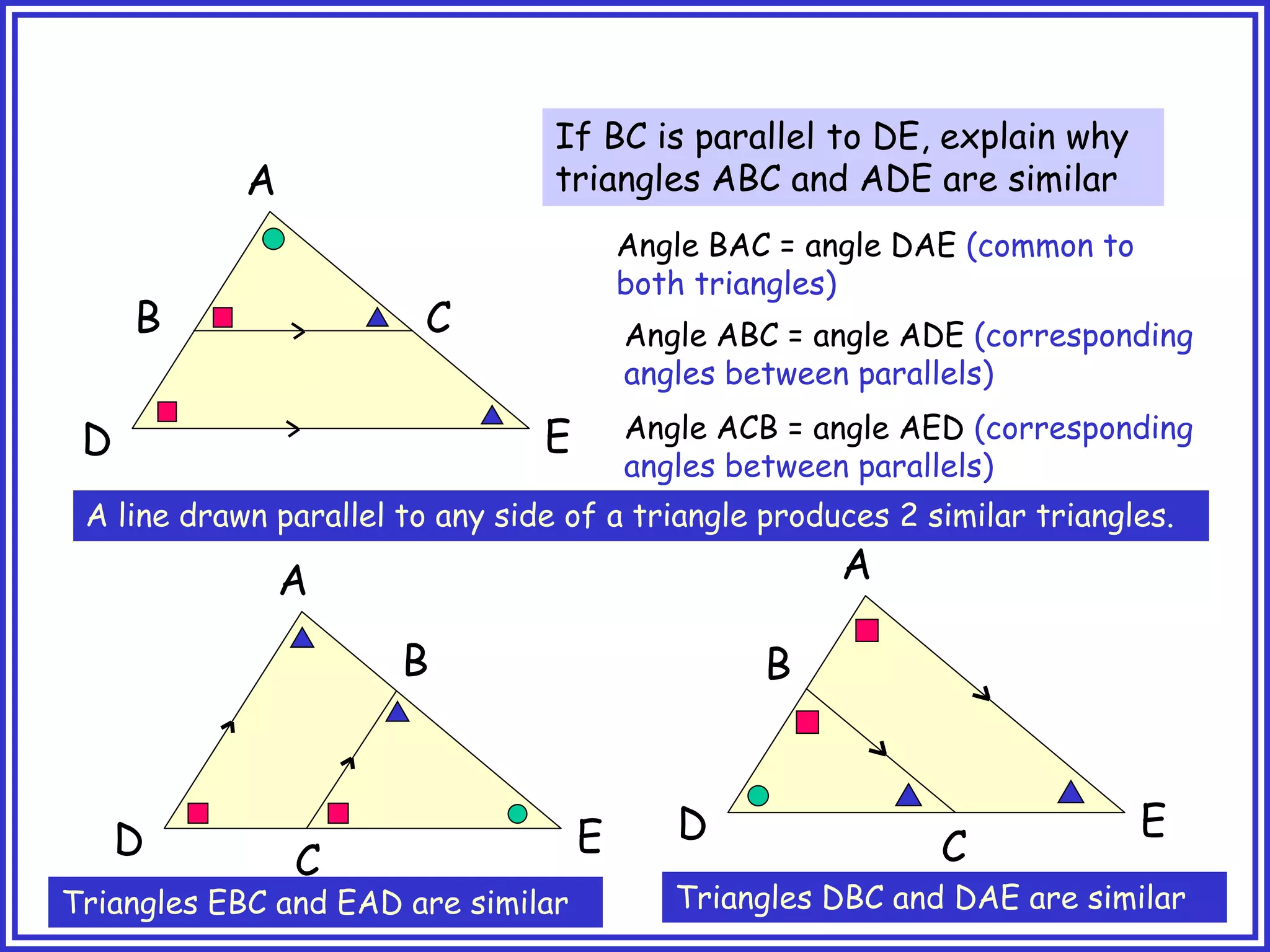
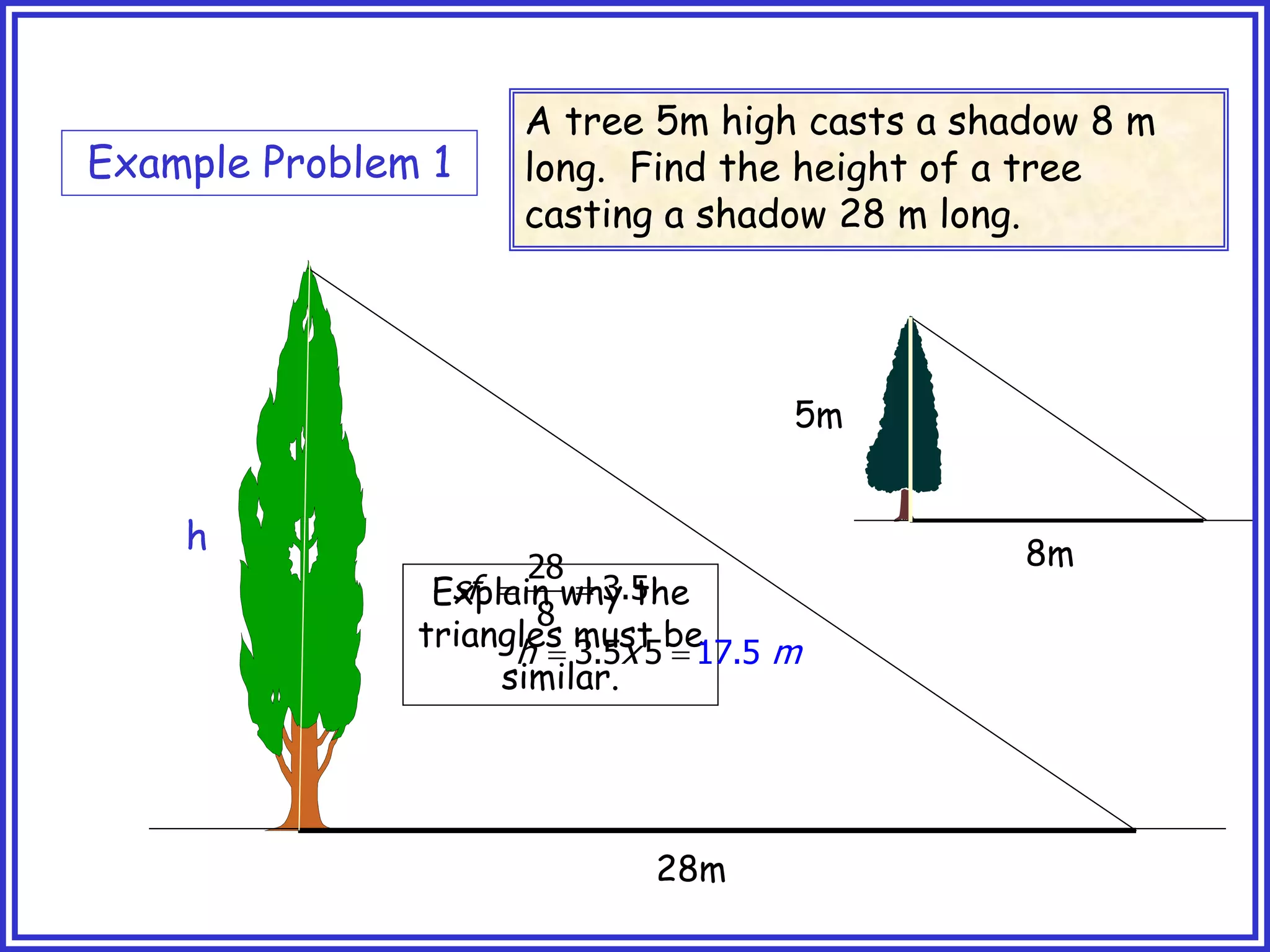
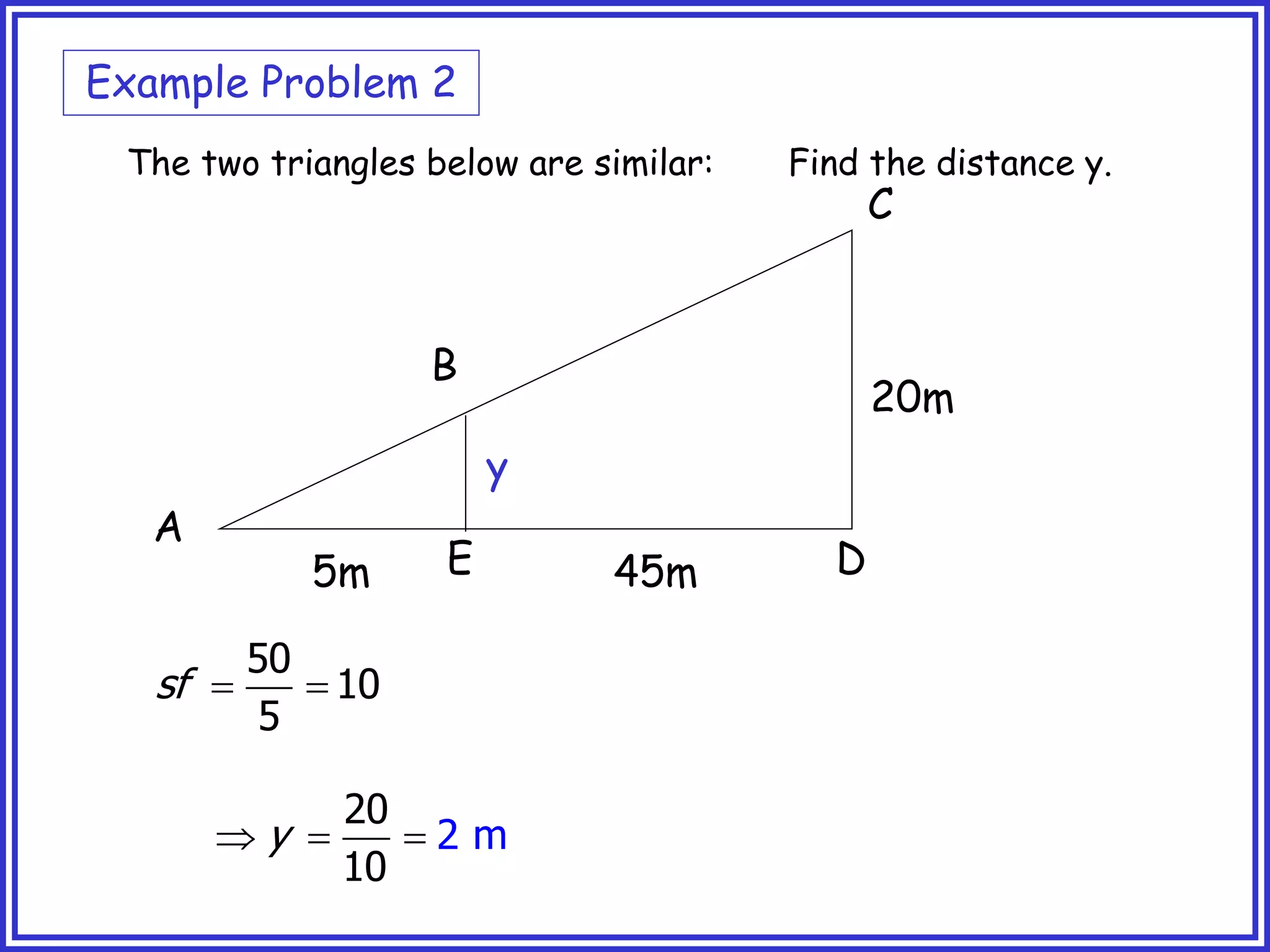
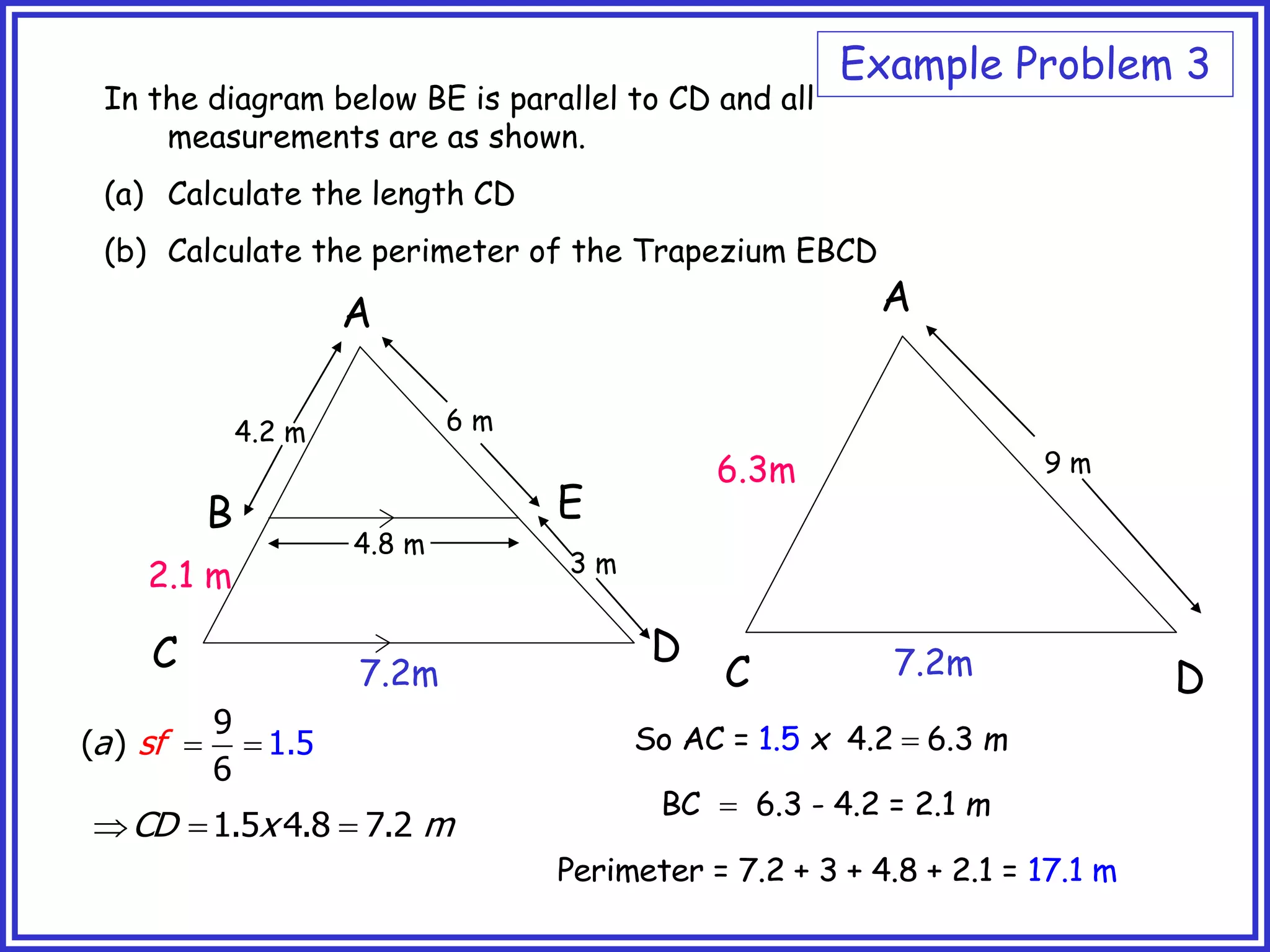
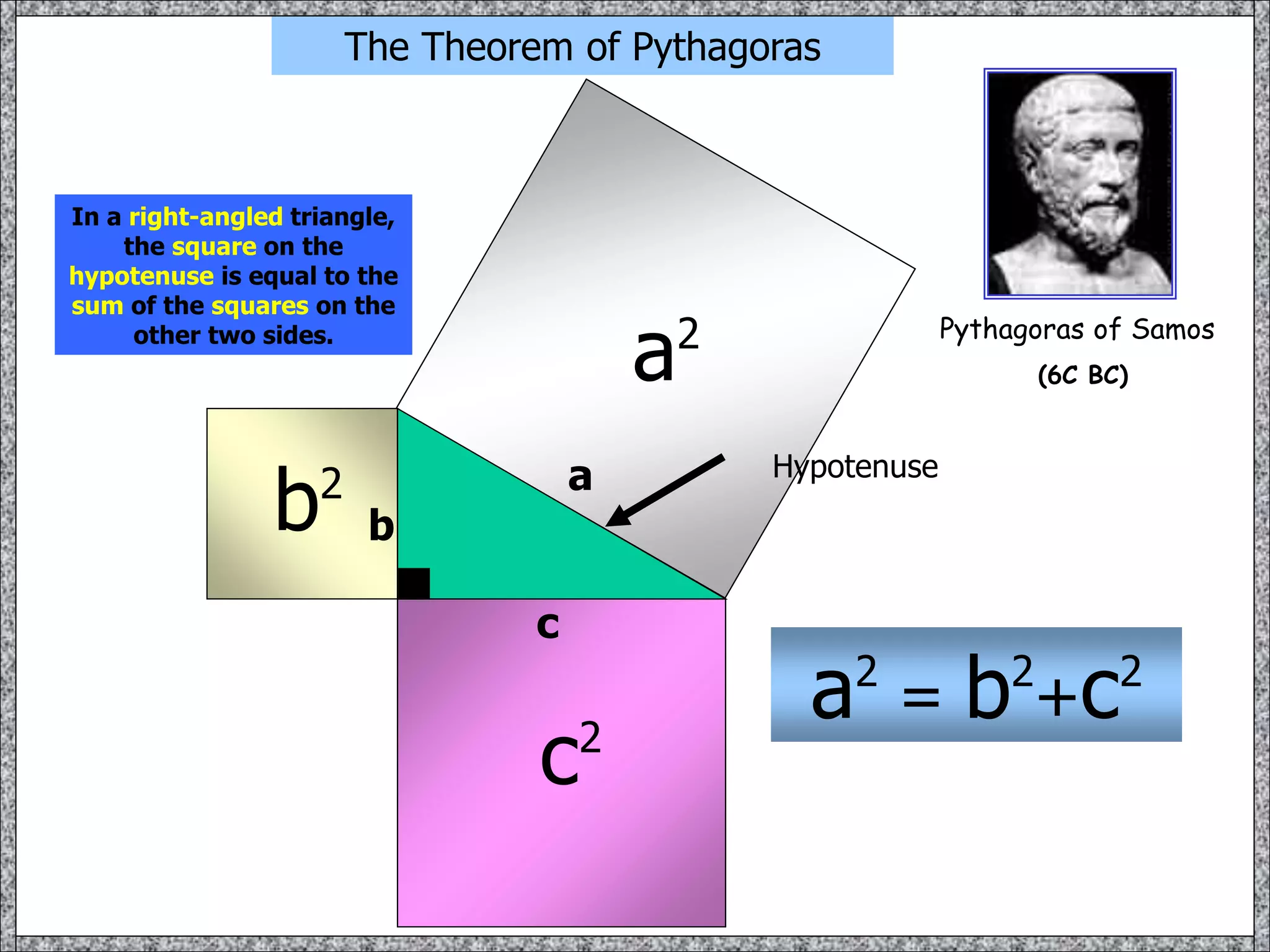
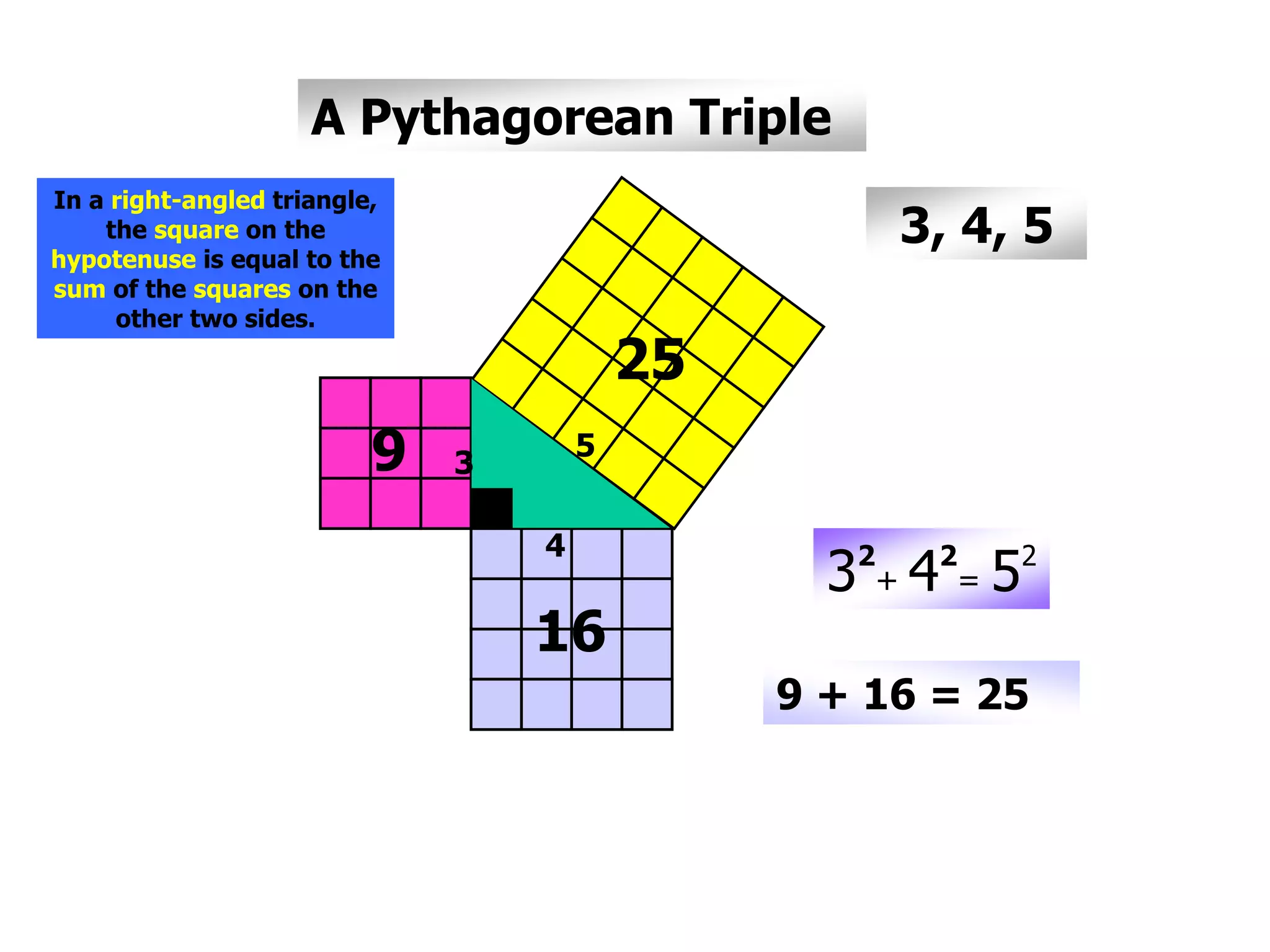
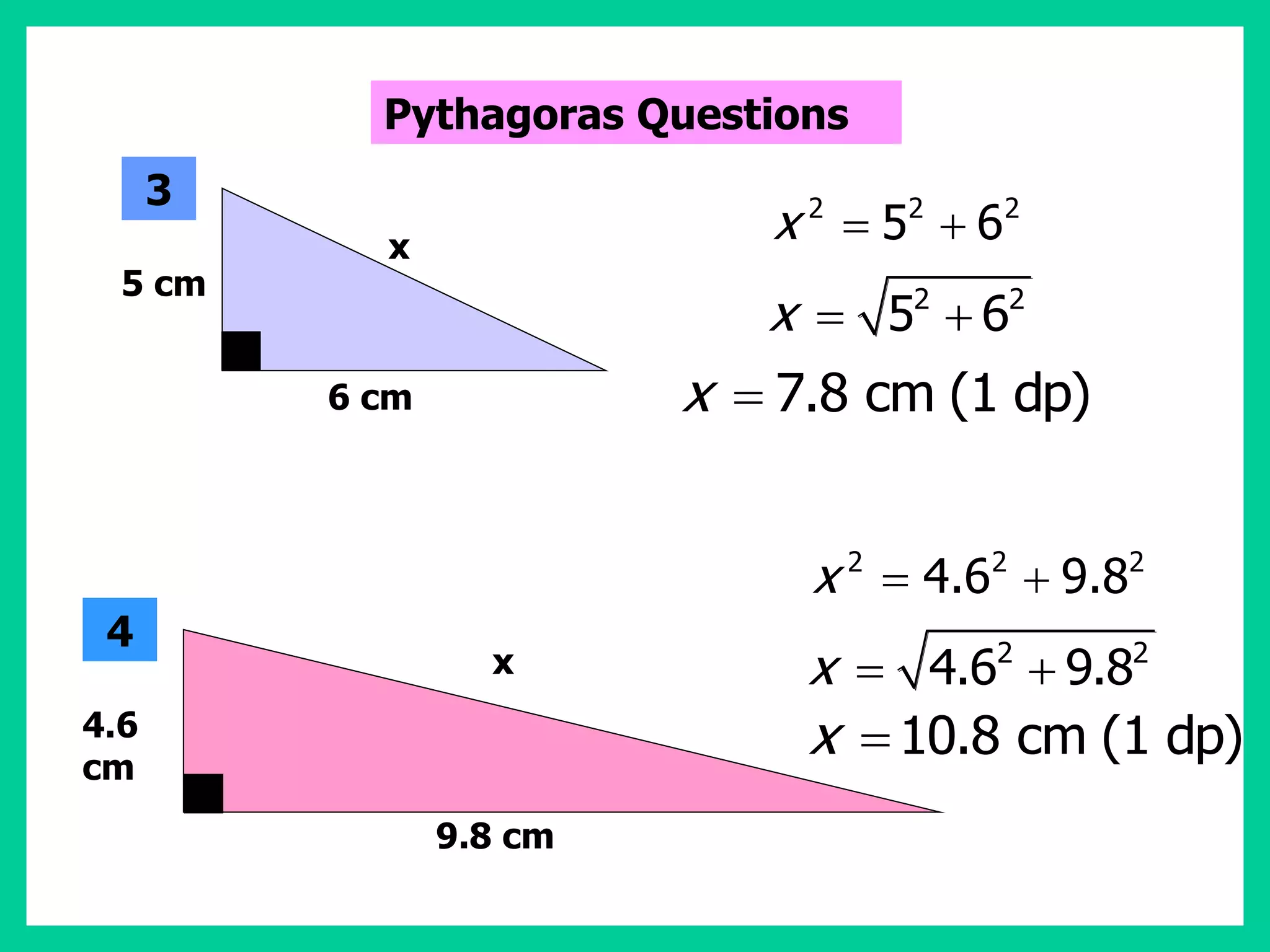
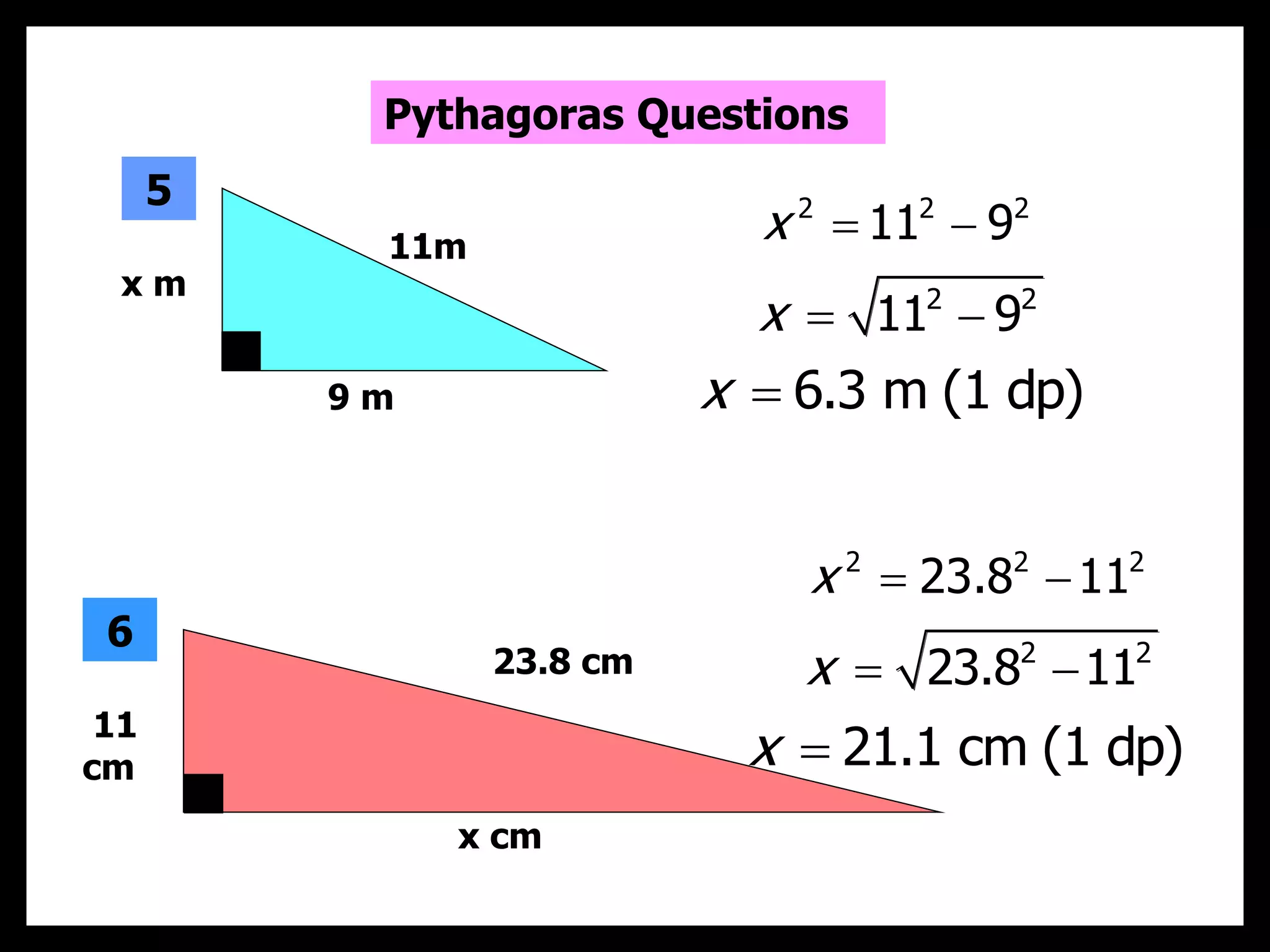
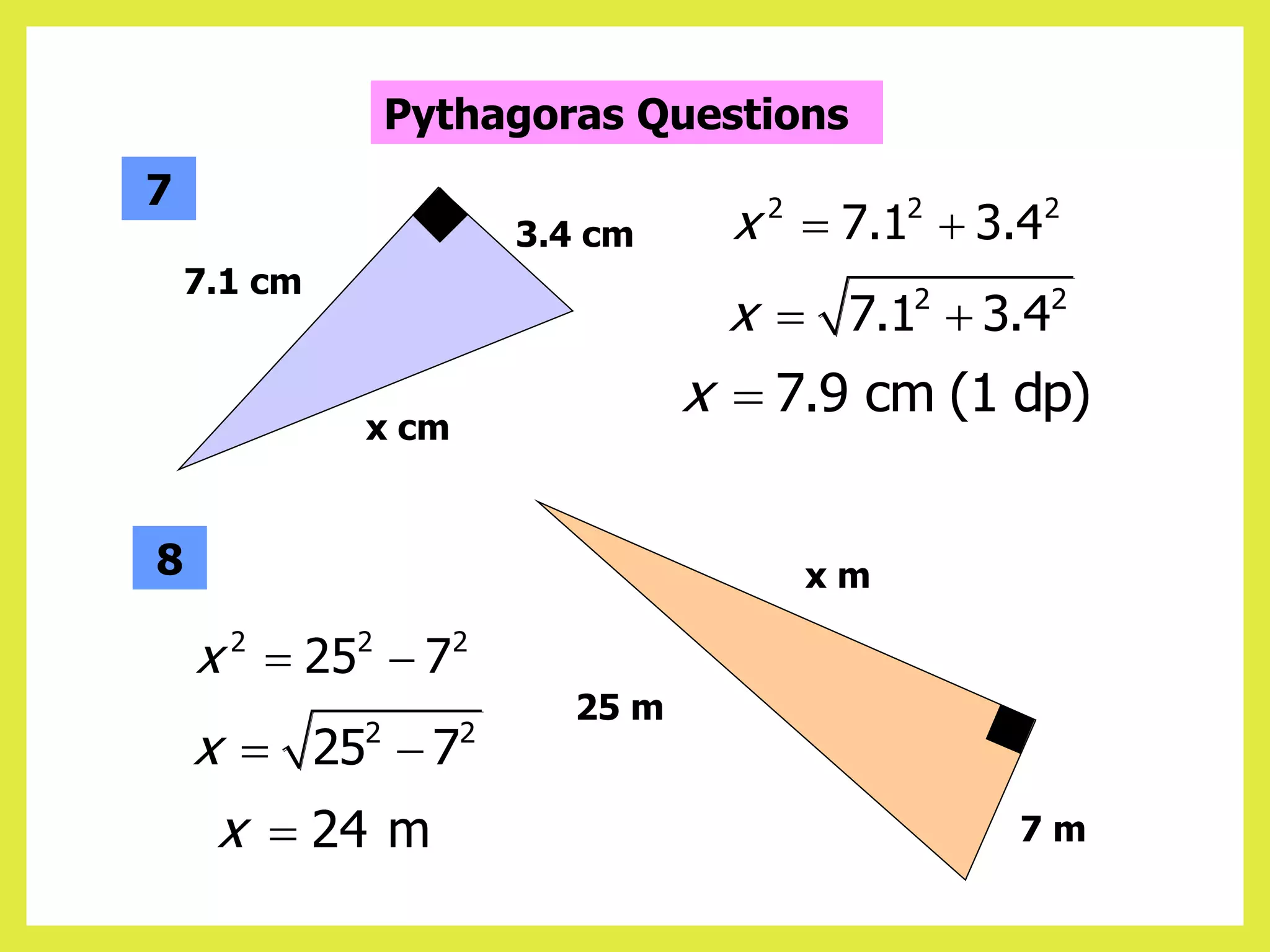
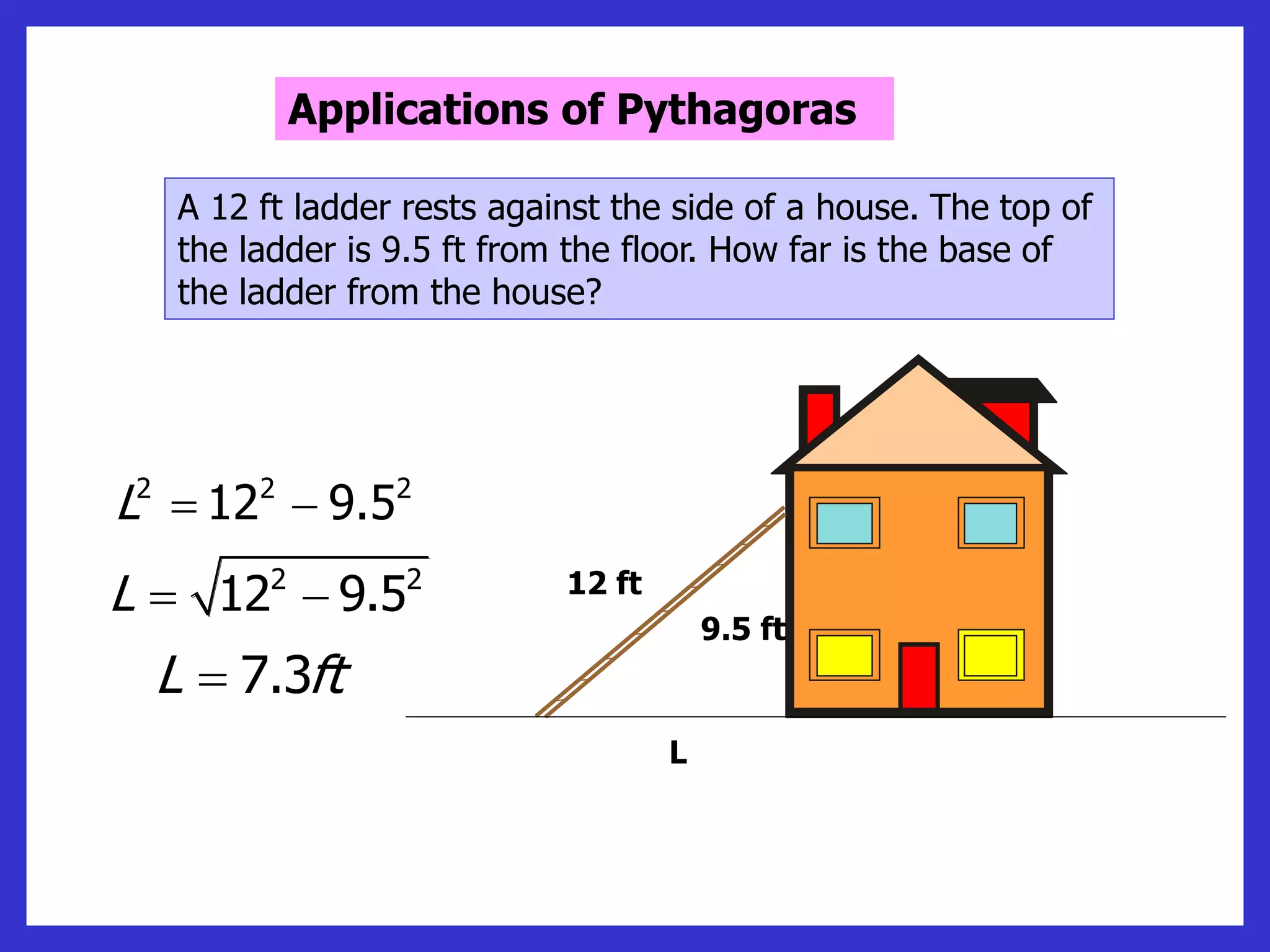
This document provides information about circle theorems developed by Euclid of Alexandria. It begins with introductory terminology for parts of a circle such as diameter, radius, circumference. It then presents 8 theorems with examples and explanations: 1) The angle in a semi-circle is a right angle, 2) The angle subtended at the centre is twice the angle at the circumference, 3) Angles subtended by an arc or chord in the same segment are equal, 4) The angle between a tangent and radius is 90 degrees, 5) The alternate segment theorem relating angles of tangents and chords, 6) The cyclic quadrilateral theorem stating opposite angles sum to 180 degrees, 7) The two tangent

1. Circle Theorems
Euclid of Alexandria
Circa 325 - 265 BC
O
The library of Alexandria was
the foremost seat of learning
in the world and functioned
like a university. The library
contained 600 000
manuscripts.

2. diameter
Circumference
radius
Major Segment
Minor Segment
Minor Arc
Major Arc
Minor Sector
Major Sector
Parts of the Circle
Parts

3. o
Arc AB subtends angle x at the centre.
A
B
xo
Arc AB subtends angle y at the circumference.
yo
Chord AB also subtends angle x at the centre.
Chord AB also subtends angle y at the circumference.
o
A
B
xo
yo
o
yo
xo
A
B
Introductory Terminology
Term’gy

4. Introductory Terminology

5. o Diameter
90o angle in a semi-circle
90o angle in a semi-circle
20o angle sum triangle
90o angle in a semi-circle
a
b
c
70o
d
30o
e
Find the unknown
angles below stating a
reason.
angle a =
angle b =
angle c =
angle d =
angle e = 60o angle sum triangle
The angle in a semi-circle is a right angle.
Theorem 1
This is just a special case of Theorem 1 and
is referred to as a theorem for convenience.
Th2

6. Theorem 2
Measure the angles at the centre and circumference and make a conjecture.
xo
yo
xo
yo
xo
yo
xo
yo
xo
yo
xo
yo
xo
yo
xo
yo
o o o o
o o o o
Th1

7. The angle subtended at the centre of a circle (by an arc
or chord) is twice the angle subtended at the
circumference by the same arc or chord. (angle at centre)
2xo
2xo 2xo
2xo
2xo 2xo
2xo 2xo
Theorem 2
Measure the angles at the centre and circumference and make a conjecture.
xo
xo
xo
xo
xo xo xo xo
o o
o o
o o o o
Angle x is subtended in the minor segment.
Watch for this
one later.

8. o
A
B
84o
xo
Example Questions
1
Find the unknown angles giving reasons for your answers.
o
A
B
yo
2
35o
42o (Angle at the centre).
70o(Angle at the centre)
angle x =
angle y =

9. (180 – 2 x 42) = 96o (Isos triangle/angle sum triangle).
48o (Angle at the centre)
angle x =
angle y =
o
A
B
42o
xo
Example Questions
3
Find the unknown angles giving reasons for your answers.
o
A
B
po
4
62o
yo
qo
124o (Angle at the centre)
(180 – 124)/2 = 280 (Isos triangle/angle sum triangle).
angle p =
angle q =

10. Angles subtended by an arc or chord in
the same segment are equal.
Theorem 3
xo
xo
xo
xo
xo
yo
yo
Th3

11. 38o
xo
yo
30o
xo
yo
40o
Angles subtended by an arc or chord in
the same segment are equal.
Theorem 3
Find the unknown angles in each case
Angle x = angle y = 38o Angle x = 30o
Angle y = 40o

12. The angle between a tangent and a
radius is 90o. (Tan/rad)
Theorem 4
o
Th4

13. The angle between a tangent and a
radius is 90o. (Tan/rad)
Theorem 4

14. 180 – (90 + 36) = 54o Tan/rad and angle sum of triangle.
90o angle in a semi-circle
60o angle sum triangle
angle x =
angle y =
angle z =
T
o
36o
xo
yo
zo
30o
A
B
If OT is a radius and AB is a
tangent, find the unknown
angles, giving reasons for your
answers.

15. The Alternate Segment Theorem.
Theorem 5
The angle between a tangent and a chord through the point of
contact is equal to the angle subtended by that chord in the
alternate segment.
xo
xo
yo
yo
45o (Alt Seg)
60o (Alt Seg)
75o angle sum triangle
Find the missing angles below
giving reasons in each case.
angle x =
angle y =
angle z = Th5

16. Cyclic Quadrilateral Theorem.
Theorem 6
The opposite angles of a cyclic quadrilateral are supplementary.
(They sum to 180o)
w
x
y
z
Angles x + w = 180o
Angles y + z = 180o
q
p
r
s
Angles p + q = 180o
Angles r + s = 180o
Th6

17. 180 – 85 = 95o (cyclic quad)
180 – 110 = 70o (cyclic quad)
Cyclic Quadrilateral Theorem.
Theorem 6
The opposite angles of a cyclic quadrilateral are supplementary.
(They sum to 180o)
85o
110o
x y
70o
135o
p
r
q
Find the missing
angles below
given reasons in
each case.
angle x =
angle y =
angle p =
angle q =
angle r =
180 – 135 = 45o (straight line)
180 – 70 = 110o (cyclic quad)
180 – 45 = 135o (cyclic quad)

18. Two Tangent Theorem.
Theorem 7
From any point outside a circle only two tangents can be drawn and
they are equal in length.
P
T
U
Q
R
PT = PQ
P
T
U
Q
R
PT = PQ
Th7

19. 90o (tan/rad)
Two Tangent Theorem.
Theorem 7
From any point outside a circle only two tangents can be drawn and
they are equal in length.
P T
Q
O
xo
wo
98o
yo
zo
PQ and PT are tangents to a circle with centre
O. Find the unknown angles giving reasons.
angle w =
angle x =
angle y =
angle z =
90o (tan/rad)
49o (angle at centre)
360o – 278 = 82o (quadrilateral)

20. 90o (tan/rad)
Two Tangent Theorem.
Theorem 7
From any point outside a circle only two tangents can be drawn and
they are equal in length.
P T
Q
O
yo
50o
xo
80o
PQ and PT are tangents to a circle with centre
O. Find the unknown angles giving reasons.
angle w =
angle x =
angle y =
angle z =
180 – 140 = 40o (angles sum tri)
50o (isos triangle)
50o (alt seg)
wo
zo

21. O
S T
3 cm
8 cm
Find length OS
OS = 5 cm (pythag triple: 3,4,5)
Chord Bisector Theorem.
Theorem 8
A line drawn perpendicular to a chord and passing through the
centre of a circle, bisects the chord..
O
Th8

22. Angle SOT = 22o (symmetry/congruenncy)
Find angle x
O
S T
22o
xo
U
Angle x = 180 – 112 = 68o (angle sum triangle)
Chord Bisector Theorem.
Theorem 8
A line drawn perpendicular to a chord and passing through the
centre of a circle, bisects the chord..
O

23. O
S
T
65o
P
R
U
Mixed Questions
PTR is a tangent line to the circle
at T. Find angles SUT, SOT, OTS
and OST.
Angle SUT =
Angle SOT =
Angle OTS =
Angle OST =
65o (Alt seg)
130o (angle at centre)
25o (tan rad)
25o (isos triangle)
Mixed
Q 1

24. 22o (cyclic quad)
68o (tan rad)
44o (isos triangle)
68o (alt seg)
Angle w =
Angle x =
Angle y =
Angle z =
O
w
y
48o
110o
U
Mixed Questions
PR and PQ are tangents to the
circle. Find the missing angles
giving reasons.
x
z
P
Q
R
Mixed Q 2

25. A
B
C
D
A B C D
Similarity
Remember, similar shapes
are always in proportion to
each other. There is no
distortion between them.

26. Conditions for similarity
Two shapes are similar only when:
•Corresponding sides are in proportion and
•Corresponding angles are equal
All regular polygons
are similar

28. Conditions for similarity
Two shapes are similar only when:
•Corresponding sides are in proportion and
•Corresponding angles are equal
All rectangles are not similar to one
another since only condition 2 is true.

29. If two objects are similar then one is an enlargement of the other
The rectangles below are similar:
Find the scale factor of enlargement that maps A to B
A
B
8 cm
16 cm
5 cm
10 cm
Not to scale!
Scale factor = x2.
(Note that B to A
would be x ½)

30. If two objects are similar then one is an enlargement of the other
The rectangles below are similar:
Find the scale factor of enlargement that maps A to B
A
B
8 cm
12 cm
5 cm
7½ cm
Not to scale!
Scale factor = x1½
(Note that B to A
would be x 2/3)

31. If we are told that two objects are similar and we can find the
scale factor of enlargement by comparing corresponding sides then
we can calculate the value of an unknown side.
8 cm
A
B
C
2 cm
Not to scale!
24 cm
p cm
q cm
12½ cm
The 3 rectangles are similar. Find the
unknown sides, p and q
1. Comparing corresponding sides in A and B. SF = 24/8 = x3.
2. Apply the scale factor to find the unknown side. p = 3 x 2 = 6 cm.

32. If we are told that two objects are similar and we can find the
scale factor of enlargement by comparing corresponding sides then
we can calculate the value of an unknown side.
8 cm
A
B
C
2 cm
Not to scale!
24 cm
p cm
q cm
12½ cm
The 3 rectangles are similar. Find the
unknown sides, p and q.
1. Comparing corresponding sides in A and C. SF = 12.5/2 = x6.25.
2. Apply the scale factor to find the unknown side. q = 6.25 x 8 = 50 cm.

33. 5 cm
If we are told that two objects are similar and we can find the
scale factor of enlargement by comparing corresponding sides then
we can calculate the value of an unknown side.
A
B
C
2.1 cm
Not to scale!
p cm
7.14 cm
35.5
cm
q cm
The 3 rectangles are similar. Find the
unknown sides p and q
1. Comparing corresponding sides in A and B. SF = 7.14/2.1 = x3.4.
2. Apply the scale factor to find the unknown side. p = 3.4 x 5 = 17 cm.

34. 5 cm
If we are told that two objects are similar and we can find the
scale factor of enlargement by comparing corresponding sides then
we can calculate the value of an unknown side.
A
B
C
2.1 cm
Not to scale!
p cm
7.14 cm
35.5
cm
q cm
The 3 rectangles are similar. Find the
unknown sides p and q
1. Comparing corresponding sides in A and C. SF = 35.5/5 = x7.1.
2. Apply the scale factor to find the unknown side. q = 7.1 x 2.1 = 14.91 cm

35. Similar Triangles
Similar triangles are important in mathematics and their
application can be used to solve a wide variety of problems.
The two conditions for similarity between shapes as
we have seen earlier are:
•Corresponding sides are in proportion and
•Corresponding angles are equal
Triangles are the exception to this rule.
Only the second condition is needed
Two triangles are similar if their
•Corresponding angles are equal

36. 70o 70o
45o
65o
45o
These two triangles are similar since
they are equiangular.
50o 55o
75o
50o
These two triangles are similar since
they are equiangular.
If 2 triangles have 2 angles the
same then they must be equiangular = 180 – 125 = 55

37. Finding Unknown Sides
20 cm
15 cm 12 cm
6 cm
b c
Since the triangles are equiangular they are similar.
So comparing corresponding sides to find the scale factor of
enlargement.
SF = 15/12 = x1.25.
b = 1.25 x 6 = 7.5 cm
c = 20/1.25 = 16 cm

38. 31.5 cm
14 cm 8 cm
6 cm
x
y
SF = 14/8 = x1.75.
x = 1.75 x 6 = 10.5 cm
y = 31.5/1.75 = 18 cm
Since the triangles are equiangular they are similar.
So comparing corresponding sides to find the scale factor of
enlargement.
Finding Unknown Sides

39. Determining similarity
A B
E D
Triangles ABC and DEC are
similar. Why?
C
Angle ACB = angle ECD (Vertically Opposite)
Angle ABC = angle DEC (Alt angles)
Angle BAC = angle EDC (Alt angles)
Since ABC is similar to DEC we know that corresponding
sides are in proportion
ABDE BCEC ACDC
The order of the lettering is important in order to show which
pairs of sides correspond.

40. A
B C
D E
If BC is parallel to DE, explain why
triangles ABC and ADE are similar
Angle BAC = angle DAE (common to
both triangles)
Angle ABC = angle ADE (corresponding
angles between parallels)
Angle ACB = angle AED (corresponding
angles between parallels)
A
D E
A
D E
B
C
B
C
A line drawn parallel to any side of a triangle produces 2 similar triangles.
Triangles EBC and EAD are similar Triangles DBC and DAE are similar

41. A tree 5m high casts a shadow 8 m
long. Find the height of a tree
casting a shadow 28 m long.
Example Problem 1
5m
8m
28m
h
Explain why the
triangles must be
similar.
 
28
3.5
8
sf
  1
3 7
.5 5
5 .
h x m

42. A
B
C
D
E
20m
45m
5m
y
The two triangles below are similar: Find the distance y.
 
50
10
5
sf
  
20
10
2 m
y
Example Problem 2

43. A
B
C D
E
In the diagram below BE is parallel to CD and all
measurements are as shown.
(a) Calculate the length CD
(b) Calculate the perimeter of the Trapezium EBCD
4.8 m
6 m
3 m
4.2 m
9 m
A
C D
7.2m 7.2m
2.1 m
6.3m
 
9
( )
6
1.5
f
a s
  
1.5 4.8 7.2
CD x m
So AC = 4.2 6 3
.5
1 .
x m

BC 6.3 - 4.2 = 2.1 m

Perimeter = 7.2 + 3 + 4.8 + 2.1 17
= .1 m
Example Problem 3

44. “All Men by nature desire knowledge”: Aristotle.
THE SCHOOL of ATHENS (Raphael) 1510 -11
Pythagoras Euclid
Plato Aristotle
Socrates

45. a2
b2
c2
a2
= b2
+c2
The Theorem of Pythagoras
b
c
a
In a right-angled triangle,
the square on the
hypotenuse is equal to the
sum of the squares on the
other two sides.
Hypotenuse
Pythagoras of Samos
(6C BC)

46. 25
9
16
32
+ 42
= 52
9 + 16 = 25
A Pythagorean Triple
3
4
5
3, 4, 5
In a right-angled triangle,
the square on the
hypotenuse is equal to the
sum of the squares on the
other two sides.

47. 169
144
25
52
+ 122
= 132
25 + 144 = 169
A 2nd Pythagorean Triple
5, 12, 13
5
12
13
In a right-angled triangle,
the square on the
hypotenuse is equal to the
sum of the squares on the
other two sides.

48. 625
576
49
72
+ 242
= 252
49 + 576 = 625
7
24
25
A 3rd Pythagorean Triple
7, 24, 25
In a right-angled triangle,
the square on the
hypotenuse is equal to the
sum of the squares on the
other two sides.

49. Perigal’s Dissection
The Theorem of Pythagoras: A Visual Demonstration
In a right-angled triangle,
the square on the
hypotenuse is equal to the
sum of the squares on the
other two sides.
Draw 2 lines through the centre of the middle square, parallel to the sides of the large square
This divides the middle square into 4 congruent quadrilaterals
These quadrilaterals + small square fit exactly into the large square
Henry Perigal
(1801 – 1898)
Gravestone
Inscription

50. 2 2 2
3 4
x  
2 2
3 4
x  
5 cm
x 
2 2 2
5 12
x  
2 2
5 12
x  
13 cm
x 
3 cm
4 cm
x
1
5 cm
12 cm
x
2
Pythagoras Questions

51. 2 2 2
5 6
x  
2 2
5 6
x  
7.8 cm (1 dp)
x 
2 2 2
4.6 9.8
x  
2 2
4.6 9.8
x  
10.8 cm (1 dp)
x 
5 cm
6 cm
x
3
4.6
cm
9.8 cm
x
4
Pythagoras Questions

52. 2 2 2
11 9
x  
2 2
11 9
x  
6.3 m (1 dp)
x 
2 2 2
23.8 11
x  
2 2
23.8 11
x  
21.1 cm (1 dp)
x 
x m
9 m
11m
5
11
cm
x cm
23.8 cm
6
Pythagoras Questions

53. 2 2 2
7.1 3.4
x  
2 2
7.1 3.4
x  
7.9 cm (1 dp)
x 
7.1 cm
x cm
3.4 cm
7
8
25 m
7 m
x m
2 2 2
25 7
x  
2 2
25 7
x  
24 m
x 
Pythagoras Questions

54. Applications of Pythagoras
Find the diagonal of the rectangle
6 cm
9.3 cm
1
2 2 2
9.3 6
d  
2 2
9.3 6
d  
11.1 cm (1 dp)
d 
d
A rectangle has a width of 4.3 cm and a diagonal of 7.8 cm. Find its perimeter.
2
7.8 cm
4.3 cm
x cm
2 2 2
7.8 4.3
x  
2 2
7.8 4.3
x  
6.5 cm (1 dp)
x 
Perimeter = 2(6.5+4.3) = 21.6 cm

55. Applications of Pythagoras
A boat sails due East from a Harbour (H), to a marker buoy (B), 15 miles away.
At B the boat turns due South and sails for 6.4 miles to a Lighthouse (L). It then
returns to harbour. Make a sketch of the journey. What is the total distance
travelled by the boat?
2 2 2
15 6.4
LH  
2 2
15 6.4
LH  
16.3 miles
LH 
Total distance travelled = 21.4 + 16.3 = 37.7 miles
H
B
L
15 miles
6.4 miles

56. 12 ft
9.5 ft
L
A 12 ft ladder rests against the side of a house. The top of
the ladder is 9.5 ft from the floor. How far is the base of
the ladder from the house?
Applications of Pythagoras
2 2 2
12 9.5
L  
2 2
12 9.5
L  
7.3
L ft


57. 5 cm
12 cm
6 cm
Find the diagonals of the kite
2 2 2
6 5
x  
5
cm
x
cm
y
cm
2 2
6 5
x  
3.32 (2 dp)
x 
short diagonal
2 6.6 (1
3.3 dp
2 )
x cm


2 2 2
12 3.32
y  
2 2
12 3.32
y  
11.53 (2 dp)
y 
long diagonal
11.5 16.5
3 5 (1 dp)
cm

 