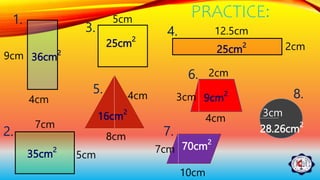
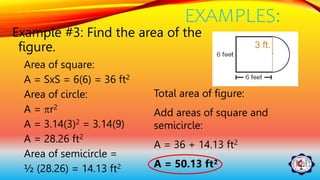
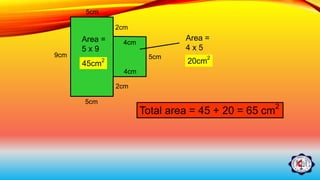
Area is measured in square units and refers to the amount of surface space a flat object has. There are formulas to calculate the area of basic plane figures like squares, rectangles, triangles, circles, and composite figures that are made up of multiple shapes. To find the area of a composite figure, you break it into its component shapes, calculate the individual areas, and add them together. The document provides examples of using formulas to find the areas of various plane figures and composite shapes.

1. MEASURING
AREA

2. ESSENTIAL QUESTIONS
What is an areas?
How do we find the area of plane
figures?

4. Area is the amount of surface space
that a flat object has.
Area is measured in square units.
1 unit
1 unit
1 unit
1 unit

5. When you measure the amount of
carpet to cover the floor of a room,
you measure it in square units.
Would the area of your bedroom
or the area of your house be
greater?
You’re right! The area of your house is
greater than the area of your bedroom.

6. Area = 15 square units
Lets find the area of this surface if
each square is equal to one unit.
Count the number of squares.
1 2
3
4 5 6 7 8
9 10 11 12 13 14
15

7. Count the number of
green squares to
determine the area of this
surface. What is the
area?
The area is equal
to 9 square units.
1
5
2
4
7
3
6
8 9

8. Two neighbors build swimming pools. This
is what the pools look like.
Family A Family B
Which family has the pool with the bigger
swimming area?
Let’s do these problems
together.

9. The area of Family A’s pool is?
Family A
Family B
8 square units.
7 square units
The area of Family B’s pool is?
Therefore, Family A has the pool with
the bigger swimming area.

10. Formulas in finding the
area of plane figures
Area of a square:
A = s x s or s²
Area of a rectangle:
A = L x W
Where s is the side of
the square.
S
Where L is the length while
W is the width of the
rectangle.
W
L

11. Formulas in finding the
area of plane figures
Area of a square:
Area of a rectangle:
4cm
3cm
5cm
EXAMPLE:
A = s x s or s²
A = 4 x 4 or 4²
A = 16 cm²
A = L x W
A = 5 x 3
A = 15 cm²

12. Formulas in finding the
area of plane figures
Area of a parallelogram:
A = B x H
Area of a triangle:
A = ½ x B x H
B B
H
Where B is the base while H
is the height of the
parallelogram.
H
Where B is the base while H
is the height of the triangle.

13. Formulas in finding the
area of plane figures
Area of a parallelogram:
Area of a triangle:
A = ½ x B x H
7m
8cm
2m 3cm
EXAMPLE:
A = 7 x 3
A = B x H
A = 21 m²
A = ½ x 8 x 3
A = ½ x 24
A = 12 cm²

14. Formulas in finding the
area of plane figures
Area of a trapezoid:
A = ½ x(b1 + b2) x H
Area of a circle:
A = 𝜋 𝑥 𝑟²
B
Where B is the base while H
is the height of the
parallelogram.
Where r is the radius of the
circle.
H r
Where 𝜋 = 3.14
B

15. Formulas in finding the
area of plane figures
Area of a trapezoid:
A = ½ x(b1 + b2) x H
6cm
3cm
EXAMPLE:
4cm A = ½ x(4 + 6) x 3
A = ½ x(10) x 3
A = 5 x 3
A = 15 cm²

16. Formulas in finding the
area of plane figures
Area of a circle:
A = 𝜋 𝑥 𝑟²
5 cm
EXAMPLE:
A = 3.14 𝑥 5²
A = 3.14 𝑥 25
A = 78.50 cm²

17. Formulas in finding the
area of plane figures
Area of a circle:
A = 𝜋 𝑥 𝑟²
8 cm
EXAMPLE:
A = 3.14 𝑥 4²
A = 3.14 𝑥 16
A = 50.24 cm²

18. 36cm2
35cm2
25cm2
25cm2
4cm
9cm
7cm
5cm
5cm
2cm
12.5cm
PRACTICE:
2cm
4cm
4cm
8cm
10cm
7cm
3cm
3cm
16cm2
9cm2
70cm2
28.26cm2
1.
2.
3. 4.
5.
6.
7.
8.

20. ESSENTIAL QUESTIONS
What is a composite figures?
How do we find the area of
composite figures?

21. Finding the area of
composite figures
Is made up of several simple geometric
figures.
Is formed from two or more figures.
COMPOSITE FIGURES

22. Subdivide the figure into simpler
shapes.
Find the areas of each figure then add
them up.
To find the area of a shaded region,
you need to subtract the areas.
TO FIND THE AREA OF A
COMPOSITE FIGURES:

23. 10cm
8cm
8cm
2cm
4cm
4cm
Area =
4 x 10
40cm2
Area =
4 x 8
32cm2
Total area = 40 + 32
= 72 cm
2
EXAMPLES:
Example #1: Find the area of the composite figure.

24. Example #2: Find the area of the
composite figure.
Area of square:
A = lw = 7(7) = 49 yd2
Total area of figure: Add up
areas of 2 triangles and
square:
A = 2(14) + 49
= 28 + 49 = 77 yd2.
Area of 1 triangle:
A = ½ bh
A = ½ (7)(4)
A = ½ (28)
A = 14 yds2
EXAMPLES:

25. Example #3: Find the area of the
figure. 3 ft.
Total area of figure:
Add areas of square and
semicircle:
A = 36 + 14.13 ft2
A = 50.13 ft²
EXAMPLES:
Area of square:
A = SxS = 6(6) = 36 ft2
Area of circle:
A = r2
A = 3.14(3)2 = 3.14(9)
A = 28.26 ft2
Area of semicircle =
½ (28.26) = 14.13 ft2

26. 8cm
area = 64 – 50.24
= 13.76 cm
2
Example #4:Find the area of the
shaded region of the figure.
A = 3.14 𝑥 4²
A = 3.14 𝑥 16
A = 50.24
A = s x s or s²
A = 8 x 8 or 8²
A = 64 cm²
cm²
EXAMPLES:
Area of square:
Area of the circle:
Area of the shaded region:

27. • What is its radius?
• Diameter = Length of square
= = 8 ft.
• Radius = ½ (8) = 4 ft.
• Area of circle:
• A = r2
• A = 3.14(4)2 = 3.14(16) ft2.
• A = 50.24 ft²
64
Area of shaded region
A = 64 – 50.24ft2.
A = 13.76ft²
d = 8 ft.
EXAMPLES:
Example #5: Find the area of the
shaded region if the area of the
square is 64 ft2.

28. 9cm
5cm
5cm
2cm
4cm
5cm
4cm
2cm
11cm
7cm
4cm
3cm 3cm
3cm
7cm
6cm
6cm
11cm
2cm
4cm
5cm
4cm
PRACTICE:
Direction: Find the area of each
figure below.

29. 20
cm
Direction: Find the area of the shaded region above.
PRACTICE:
3cm

30. 9cm
5cm
5cm
2cm
4cm
5cm
4cm
2cm
Area =
5 x 9
45cm
2
Area =
4 x 5
20cm
2
Total area = 45 + 20 = 65 cm2

31. 6cm
6cm
11cm
2cm
4cm
5cm
Area =
2 x 5
10cm2
Area =
6 x 6
36cm2
Total area = 10 + 36 = 46 cm2

32. 11cm
7cm
4cm
3cm 3cm
3cm
7cm
Total area = 28 + 16 + 21 = 65 cm2
Area =
4 x 7
Area =
4 x 4
4cm
Area =
3 x 7
21cm2
28cm
2
16cm
2

33. 20
cm
A = ½bh
A = ½ 30(20)
A = 15(20)
A = L(W)
A = 30 x 20
A = 600 cm²
cm²
A = 300
Area of rectangle
Area of triangle
Area of the shaded region:
A = 600 – 300
A = 300 cm²

34. 3cm
A = 3.14 𝑥 3²
A = 3.14 𝑥 9
A = 28.26
A = s x s or s²
A = 2 x 2 or 2²
A = 4 cm²
cm²
Area of circle
Area of square
Area of the shaded region:
A = 28.26 – 4
A = 24.26cm²

35. REMINDER!!!
STUDY FOR A DIGITAL
QUIZ ON FRIDAY.
 MEASURING AREA AND
 SPEED, DISTANCE AND TIME

36. PRACTICE: