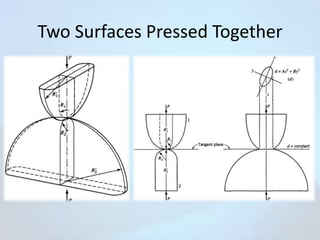
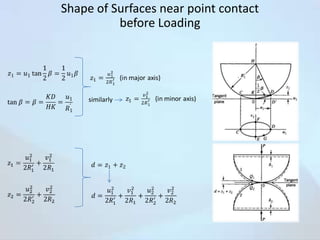
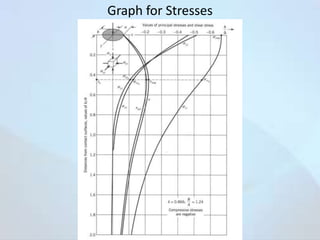
The document discusses contact stresses that occur between two surfaces pressed together, such as between a locomotive wheel and rail. It provides examples where contact stresses are significant, like in bearings and gears. When surfaces are pressed together, high stresses develop just below the surface at the point of contact. These stresses can cause failures like cracking or pitting. The document presents equations to calculate the principal stresses that develop from an elliptical stress distribution between the pressed surfaces. Factors like the curvature of the surfaces and angle of contact are considered. Charts are also included showing stress distribution parameters for different angles of contact.

1. CONTACT STRESSES
Between Two Surfaces Presses Together
Muhanned Mahdi
Instructor : Professor Satchi
Venkataraman

2. Two Surfaces Pressed Together
• The contact stresses created when surfaces of two bodies are pressed
together by external loads are the significant stresses; that is, the stresses on
Or somewhat beneath the surface of contact are the major causes of failure
of one or both of the bodies.
• The examples where contact stresses maybe significant at the area :
1.
2.
3.
4.
between a locomotive wheel and the railroad rail.
between a roller or ball and its race in a bearing.
between the teeth of a pair of gears in mesh.
between the cam and valve tappets of a gasoline engine.

3. Two Surfaces Pressed Together
•
For example, a railroad rail
sometimes fails as a result of
“contact stresses”; the failure
starts as a localized fracture in
the form of a minute transverse
crack at a point in the head of
the rail somewhat beneath the
surface of contact between the
rail and locomotive wheel. This
fracture progresses outwardly
under the influence of the
repeated wheel loads until the
entire rail cracks or fractures.
This fracture is called a
transverse fissure failure

4. Two Surfaces Pressed Together
• In contrast, bearings and gear
teeth sometimes fail as a result
of formation of pits (pitting) at
the surface of contact. The
bottom of such a pit is often
located approximately at the
point of maximum shear stress.
Steel tappets have been
observed to fail by initiation of
microscopic cracks at the
surface that then spread and
cause flaking. Chilled cast-iron
tappets have failed by cracks
that start beneath the surface,
where the shear stress is
highest, and spread to the
surface, causing pitting failure

5. Assumptions
1. Load
•
It is assumed that there is no tendency for one body to slide with
respect to the other and, hence, no friction force is present.
There is no effect of a friction force.
2. Properties of Materials
•
The material of each body is homogeneous, isotropic, and elastic
in accordance with Hooke’s law, but the two bodies are not
necessarily made of the same material.
3. Shape of Surfaces near Point of Contact before Loading
•
If two bodies are in contact at a point, there is a common tangent
plane to the surfaces at The point of contact. In the solution for
contact stresses, an expression for the distance Between
corresponding points on the surfaces near the point of contact is
required.

6. Two Surfaces Pressed Together

7. Shape of Surfaces near point contact
before Loading
similarly

8. Geometry of the contact

9. Geometry of the contact
should be
equal to

10. Geometry of the contact
• The constants A and B depend on the principal radii of curvature of the two bodies at
the point of contact and on the angle a between the corresponding planes of the
principal curvatures.

11. •
A general equation for displacements according
to geometrical considerations can be written as
•
Since we know that
we can write the equation as :
•
The surface displacement for Hertz
pressure can be written as :
•
Then the equation for vertical displacements become :
, then

12. Equations for Principal Stresses
• To satisfy the vertical displacement equilibrium,
an elliptical stress distribution is required :
• Then the principal stresses become as follows :

13. Equations for Principal Stresses
• The major and minor axis of the area of contact can be defined as follows :
θ (degree)
30
35
40
45
50
55
60
65
70
75
80
85
90
m
2.731
2.397
2.136
1.928
1.754
1.611
1.486
1.378
1.284
1.202
1.128
1.061
1
n
0.493
0.53
0.567
0.604
0.641
0.678
0.717
0.759
0.802
0.846
0.893
0.944
1

14. Graph for Stresses