Uploaded bywidi1966
PPT, PDF19,162 views

1. Penyajian Data Statistik

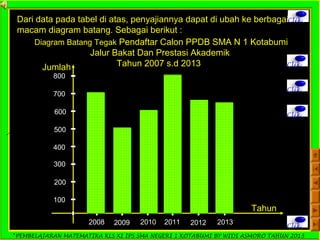
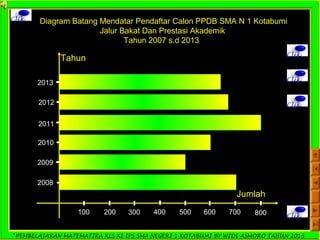
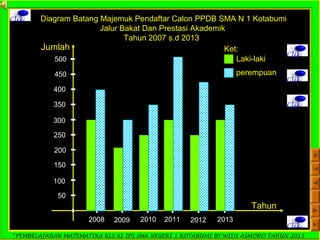
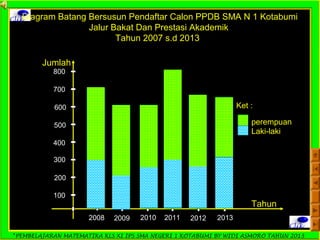
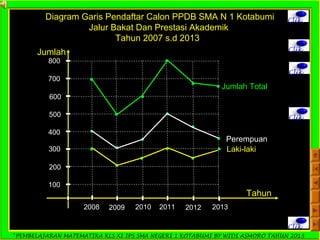
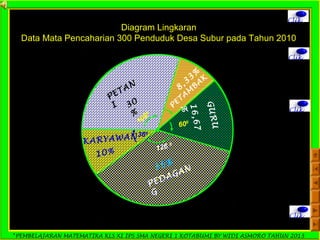
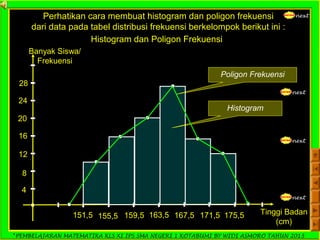
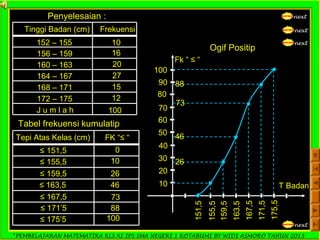
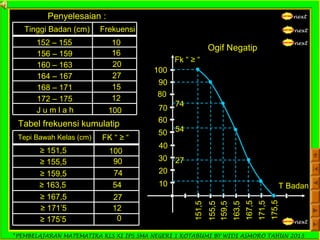
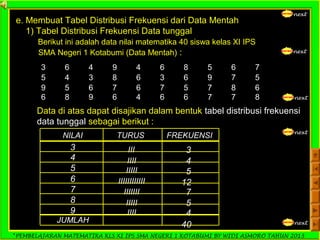
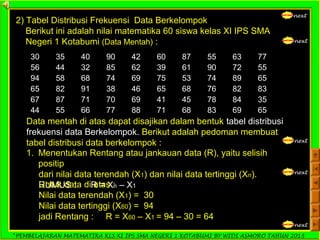
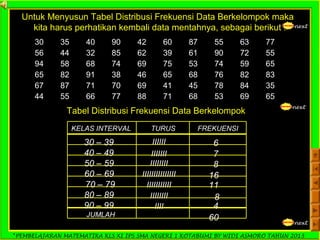
Dokumen ini adalah panduan pembelajaran matematika untuk siswa kelas XI IPS di SMA Negeri 1 Kotabumi, yang difokuskan pada statistika. Terdapat penjelasan mengenai pengertian statistik, jenis data, pengumpulan data, serta teknik penyajian data dalam bentuk tabel dan diagram. Materi ini bertujuan untuk membantu siswa memahami dasar-dasar pengolahan dan analisis data.

Embed presentation

Downloaded 326 times
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clik SELAMAT DATANG DI MEDIA PEMBELAJARAN MATEMATIKA SMA NEGERI 1 KOTABUMI LAMPUNG UTARA BERSAMA WIDI ASMORO. S.Pd TAHUN 2013 DALAM POKOK BAHASAN STATISTIKA KELAS XI IPS
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 ClikSTATISTIKA 1. Pengertian Statistik dan Statistika Statistik adalah bilangan – bilangan yang melukiskan suatu keadaan atau persoalan tertentu. Misalnya untuk melukiskan keadaan jumlah penduduk suatu negara setiap tahun dinyatakan dengan bilangan (disebut statistik), banyaknya calon siswa baru yang mendaftar di SMA Negeri 1 Kotabumi tahun pelajaran 2013/2014 melalui jalur tes adalah 542 orang ( 542 disebut statistik ). Dan lain sebagainya. Clik Adapun Statistika berasal dari kata “ Statistik” dan “ logika “ yang dapat diartikan sebagai ilmu statistik, yaitu ilmu yang mempelajari tentang bagai mana cara mengumpulkan data, menyajikan data, mengolah data, menganalisa data dan menarik kesimpulan berdasarkan data yang ada sehingga dapat diambil tindakan atau putusan yang tepat terhadap suatu persolan yang sedang diteliti. Clik 2. Istilah –Istilah Yang Terdapat Dalam Statistika a. Data atau Datum Data adalah bentuk jamak dari “Datum” yang artinya adalah kumpulan keterangan atau imformasi yang diperoleh dari suatu penelitian. Clik
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clik Berdasarkan jenisnya data dibedakan menjadi 2 jenis, yaitu data kualitatif dan data kuantitatif. Clik 1) Data kualitatif, yaitu data yang tidak atau bukan bermentuk bilangan, misalnya data tentang mutu hasil panen padi di suatu kabupaten, data tentang mutu barang elektronik di gudang suatu perusahan eleektronik, dan lain sebagainya. Untuk menggambarkan data kualitatif biasanya digunakan kata-kata seperti : “ baik “, “buru”, “rusak” ,dll. Clik2) Data kuantitatif, yaitu data yang berbentu bilangan atau angka. Misalnya data tentang jumlah penduduk di suatu negara, data banyaknya kecelakaan lalu lintas, data tentang suhu badan pasien penyakit tipus. Dll. Clik Data kuantitatif dibedakan menjadi 2 macam, yaitu data diskrit dan data kontinu. Data diskrit adalah data yang diperoleh dari hasil mencacah atau menghitung, misalnya data tentang banyaknya buku yang ada di perpustakan. Data kontinu adalah data yang diperoleh dari hasil pengukuran, misalnya data tentang tinggi badan siswa, data tentang suhu badan pasien, dll. Clik
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clikb. Populasi dan Sampel Populasi adalah himpunan atau kumpulan semua objek yang sedang menjadi bhan penelitian atau pengamatan. Sedangkan Sampel adalah bagian dari populasi yang sedang diamati atau diteliti dan dapat mewakili populasi. Clik Sebagai contoh : Dalam sebuah penelitian tentang rata-rata tinggi badan siswa SMA di propinsi Lampung, Maka sebagai populasi adalah semua siswa SMA sepropinsi Lampung sedangkan sampelnya dapat dipilih secara acak sebuah SMA yang ada di propinsi Lampung, mislanya terpilih SMA Negeri 1 kotabumi sebagai sampel, berarti SMA Negeri 1 Kotabumi mewakili populasi.Clik c. Pengumpulan data ada 2 metode dalam pengumpulan data. Yaitu metode sensus dan metode sampling. Sensus adalah metode pengumpulan data dengan meneliti atau mengamati setiap anggota populsi. Sampling adalah metode pengumpulan data dengan meneliti sampel atau sebagian yang mewakili populasi. Clik
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clik d. Teknik Pengumpulan Data Ada beberapa teknik pengumpulan data dalam sebuah penelitian, antara lain : 1) interpiew atau wawancara, yaitu suatu teknik pengumpulan data dengan cara bertanya langsung kepada responden face to face tentang informasi yang diperlukan dari daftar pertanyaan yang sudah dipersiapkan sebelimnya. Clik 2) Kuisoner atau angket, yaitu suatu teknik pengumpulan data dengan cara memberi responden daftar pertanyaan yang dicetak dalam selembar atau dua lembar kertas dengan pertanyaan yang sama seperti pada wawancara Clik 3) Obsevasi langsung atau pengamatan langsung, yaitu suatu teknik pengumpulan data dengan cara mengamati objek yang sedang diteliti secara langsung dengan panca indera. Teknik ini biasanya digunakan untuk penelitian yang berkaitan dengan bidang IPA . Misalnya meneliti air sebuah sungai apakah tercemar limbah beracun atau tidak tentu tidak dapat dilakukan dengan wawancara atau angket dalam pengumpulan datanya. Clik
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clik2. Menyajikan Data Tunggal dalam Bentuk Tabel dan Diagram Agar mudah pahami orang lain Data statistik yang sudah dikumpulkan biasanya disajikan dalam bentuk tabel atau diagram. Clik a. Diagram Batang Diagram batang adalah diagram berbentuk batang atau balok. Diagram batang biasanya digunakan untuk membandingkan antar nilai data. Diagram batang dapat berbentuk tunggal, majemuk atau bertingkat. Berikut ini contoh-contoh diagram batang : Clik Contoh : Berikut adalah tabel data tentang banyaknya pendaftar PPDB SMA Negeri 1 Kotabumi jalur bakat dan prestasi akademik dari tahun 2007 sampai dengan 2013 TAHUN 2008 2009 2010 2011 2012 2013 LAKI-LAKI PEREMPUAN JUMLAH 300 400 700 200 300 500 250 350 600 300 500 800 250 425 675 300 350 650 Tabel Pendaftar Calon PPDB SMA N 1 Kotabumi Jalur Bakat Dan Prestasi Akademik Tahun 2007 s.d 2013 Clik Clik
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 ClikDari data pada tabel di atas, penyajiannya dapat di ubah ke berbagai macam diagram batang. Sebagai berikut : Diagram Batang Tegak Pendaftar Calon PPDB SMA N 1 Kotabumi Jalur Bakat Dan Prestasi Akademik Tahun 2007 s.d 2013 Clik Tahun Jumlah Clik 2008 2009 2010 2011 2012 2013 100 200 300 400 500 600 700 800 Clik Clik
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clik Diagram Batang Mendatar Pendaftar Calon PPDB SMA N 1 Kotabumi Jalur Bakat Dan Prestasi Akademik Tahun 2007 s.d 2013 Clik Jumlah Tahun Clik 100 200 300 400 500 600 2008 2009 2010 2011 2012 2013 Clik Clik 700 800
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clik Diagram Batang Majemuk Pendaftar Calon PPDB SMA N 1 Kotabumi Jalur Bakat Dan Prestasi Akademik Tahun 2007 s.d 2013 Clik Tahun Jumlah Clik 2008 2009 2010 2011 2012 2013 50 100 150 200 250 300 350 400 Clik Clik 450 500 Ket: Laki-laki perempuan
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clik Clik Diagram Batang Bersusun Pendaftar Calon PPDB SMA N 1 Kotabumi Jalur Bakat Dan Prestasi Akademik Tahun 2007 s.d 2013 Tahun Jumlah 2008 2009 2010 2011 2012 2013 100 200 300 400 500 600 700 800 Ket : Laki-laki perempuan
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clikb. Diagram Garis Diagram garis atau grafik adalah diagram berbentuk garis. Diagram garis biasanya digunakan untuk menyajikan data yang diperoleh dari berdasarkan pengamatan dari waktu ke waktu secara berurutan : Clik Contoh : Berikut adalah tabel data tentang banyaknya pendaftar PPDB SMA Negeri 1 Kotabumi jalur bakat dan prestasi akademik dari tahun 2007 sampai dengan 2013 TAHUN 2008 2009 2010 2011 2012 2013 LAKI-LAKI PEREMPUAN JUMLAH 300 400 700 200 300 500 250 350 600 300 500 800 250 425 675 300 350 650 Tabel Pendaftar Calon PPDB SMA N 1 Kotabumi Jalur Bakat Dan Prestasi Akademik Tahun 2007 s.d 2013 Clik Data pada tabel di atas dapat disajikan dalam bentuk diagram garis, sebagai berikut :
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 ClikDiagram Garis Pendaftar Calon PPDB SMA N 1 Kotabumi Jalur Bakat Dan Prestasi Akademik Tahun 2007 s.d 2013 Clik Tahun Jumlah 2008 2009 2010 2011 2012 2013 100 200 300 400 500 600 700 800 Clik Laki-laki Clik Perempuan Jumlah Total Clik
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clikc. Diagram Lingkaran Diagram lingkaran adalah diagram berbentuk daerah lingkaran. Daerah lingkaran dibagi dalam juring-juring lingkaran. Luas setiap juring lingkaran biasanya dinyatakan dalam persen : Clik Contoh : Data mata pencaharian 300 penduduk desa Subur pada tahun 2010 ditunjukan pada tabel berikut : Mt Pencaharian frekuensi petani petambak pedagangguru karyawan jumlah 90 25 50 105 30 300 Clik Untuk membuat diagram lingkaran dari data pada tabel di atas , perlu kita lakukan langkah berikut : Mata Pencaharian petani petambak guru pedagang karyawan Besar sudut pusat juring persentase 90 /300 x 3600 = 1080 25 /300 x 3600 = 300 50 /300 x 3600 = 600 105 /300 x 3600 = 1260 30 /300 x 3600 = 360 90 /300 x 100% = 30% 25 /300 x 100% = 8,33% 50 /300 x 100% = 16,67% 105 /300 x 100% = 35% 30 /300 x 100% = 10% Clik
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clik Diagram Lingkaran Data Mata Pencaharian 300 Penduduk Desa Subur pada Tahun 2010 108 0 30 % Clik PETAN I P ETA M B A K 8 ,3 3 % GURU 16,67 % Clik 126 0 PEDAGAN G 35% 360 KARYAWAN 10% Clik 600
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clik3. Membaca dan Menyajikan Data kelompok dalam Bentuk Tabel dan Diagram Data kelompok merupakan data yang ditulis dalam suatu interval. Data kelompok sering digunakan untuk menyajikan data dalam jumlah banyak ( besar ). Clik a. Tabel atau Daftar distribusi Frekuensi Data Kelompok Berikut ini contoh tabel distribusi frekuensi data berkelompok. ClikData Tinggi Badan 100 Siswa kelas XI SMA Negeri 1 Kotabumi TP 2011/2012 Clik Tinggi Badan (cm) Frekuensi 152 – 155 10 156 – 159 16 160 – 163 20 164 – 167 27 168 – 171 15 172 – 175 12 J u m l a h 100
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 next b. Beberapa istilah yang terdapat dalam tabel distribusi frekuensi data berkelompok. Tinggi Badan (cm) Frekuensi 152 – 155 10 156 – 159 16 160 – 163 20 164 – 167 27 168 – 171 15 172 – 175 12 J u m l a h 100 next 1) Kelas Interval , yaitu nilai data yang ditulis dalam bentuk interval. Contoh pada daftar di atas : 152 – 155 Kelas interval ke – 1 156 – 159 Kelas interval ke – 2 160 – 163 Kelas interval ke – 3 172 – 175 Kelas interval ke – 7 next
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 next 2) Batas Bawah Kelas Interval , yaitu nilai data yang terletak disebelah kiri setiap kelas interval. Contoh pada daftar di atas : 152 Batas Bawah Kelas interval ke – 1 156 Batas Bawah Kelas interval ke – 2 160 Batas Bawah Kelas interval ke – 3 172 Batas Bawah Kelas interval ke – 7 next 3) Batas Atas Kelas Interval , yaitu nilai data yang terletak disebelah kanan setiap kelas interval. Contoh pada daftar di atas : 155 Batas Atas Kelas interval ke – 1 159 Batas Atas Kelas interval ke – 2 163 Batas Atas Kelas interval ke – 3 175 Batas Atas Kelas interval ke – 7 next 4) Tepi Bawah Kelas Interval , yaitu nilai yang diperoleh dari batas bawah dikurangi 0,5 pada setiap kelas interval. Contoh pada daftar di atas : 152 – 0,5 = 151,5 Tepi Bawah Kelas interval ke – 1 156 – 0,5 = 155,5 Tepi Bawah Kelas interval ke – 2 172 – 0,5 = 171,5 Tepi Bawah Kelas interval ke – 7 next
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 next 5) Tepi Atas Kelas Interval , yaitu nilai yang diperoleh dari batas atas ditambah 0,5 pada setiap kelas interval. Contoh pada daftar di atas : 155 + 0,5 = 155,5 Tepi Atas Kelas interval ke – 1 159 + 0,5 = 159,5 Tepi Atas Kelas interval ke – 2 175 + 0,5 = 175,5 Tepi Atas Kelas interval ke – 7 next 6) Titik Tengah Kelas Interval , yaitu nilai yang diperoleh dari setengah kali jumlah batas bawah dan batas atas kelas interval. Contoh pada daftar di atas : ½(152 + 155) = 153,5 Titik Tengah Kelas interval ke – 1 ½(156 + 159) = 157,5 Titik Tengah Kelas interval ke – 2 ½(172 + 175) = 173,5 Titik Tengah Kelas interval ke – 7 next 7) Panjang Kelas atau Lebar Kelas , yaitu nilai yang diperoleh dari selisih positip tepi bawah dan tepi atas kelas interval. Contoh pada daftar di atas : 155,5 – 151,5 = 4 Titik Tengah Kelas interval ke – 1 159,5 – 155,5 = 4 Titik Tengah Kelas interval ke – 2 175,5 – 171,5 = 4 Titik Tengah Kelas interval ke – 7 next
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 nextc. Histogram dan Poligon Frekuensi Dari tabel distribusi frekuensi data berkelompok dapat dibuat diagram yang bernama Histogram. Histogram adalah diagram yang berupa batang – batang atau persegipanjang – persegipanjang tegak yang saling berimpit. Lebar persegipanjang sebanding dengan lebar kelas dan tinggi persegipanjang sebanding dengan besar frekuesi kelas interval masing – masing. Sedangkan Poligon Frekuensi adalah garis patah – patah yang menghubungkan titik tengah – titik tengah sisi atas histogram. next Sebagai contoh, kita akan buat histogram dan poligon frekuensi dari data pada tabel distribusi frekuensi berkelompok berikut ini : Tinggi Badan (cm) Frekuensi 152 – 155 10 156 – 159 16 160 – 163 20 164 – 167 27 168 – 171 15 172 – 175 12 J u m l a h 100 next
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 nextPerhatikan cara membuat histogram dan poligon frekuensi dari data pada tabel distribusi frekuensi berkelompok berikut ini : Histogram dan Poligon Frekuensi Tinggi Badan (cm) Banyak Siswa/ Frekuensi 151,5 155,5 159,5 163,5 167,5 171,5 175,5 4 8 12 16 20 24 28 next Histogram next Poligon Frekuensi next
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 next d. Frekuensi Kumulatif dan Ogif 1) Frekuensi Kumulatif kurang Dari dan Ogif Positip Frekuensi kumulatif kurang dari ( fk ≤ ) adalah jumlah frekuensi yang memiliki nilai kurang dari atau sama dengan nilai tepi atas suatu kelas interval. Dari tabel distribusi frekuensi kumulatif kurang dari dapat dibuat sebuah kurva mulus yang disebut Ogif Positip. nextContoh : Membuat tabel distribusi Frekuensi Kumulatif kurang Dari dan Ogif Positip dari tabel distribusi frekuensi berkelompok berikut ini. Tinggi Badan (cm) Frekuensi 152 – 155 10 156 – 159 16 160 – 163 20 164 – 167 27 168 – 171 15 172 – 175 12 J u m l a h 100 next
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 nextPenyelesaian : Tinggi Badan (cm) Frekuensi 152 – 155 10 156 – 159 16 160 – 163 20 164 – 167 27 168 – 171 15 172 – 175 12 J u m l a h 100 Tabel frekuensi kumulatip Tepi Atas Kelas (cm) FK “≤ “ ≤ 151,5 0 ≤ 155,5 10 ≤ 159,5 26 ≤ 163,5 46 ≤ 167,5 73 ≤ 171’5 88 100≤ 175’5 next Ogif Positip T Badan Fk “ ≤ “ 151,5 155,5 159,5 163,5 167,5 171,5 175,5 10 20 30 40 50 60 70 80 90 100 next next 26 46 73 88
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 next 2) Frekuensi Kumulatif Lebih Dari dan Ogif Negatif Frekuensi kumulatif kurang dari ( fk ≥ ) adalah jumlah frekuensi yang memiliki nilai lebih dari atau sama dengan nilai tepi bawah suatu kelas interval. Dari tabel distribusi frekuensi kumulatif lebih dari dapat dibuat sebuah kurva mulus yang disebut Ogif Negatip. next Contoh : Membuat tabel distribusi Frekuensi Kumulatif lebih Dari dan Ogif negatip dari tabel distribusi frekuensi berkelompok berikut ini. Tinggi Badan (cm) Frekuensi 152 – 155 10 156 – 159 16 160 – 163 20 164 – 167 27 168 – 171 15 172 – 175 12 J u m l a h 100 next
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 nextPenyelesaian : Tinggi Badan (cm) Frekuensi 152 – 155 10 156 – 159 16 160 – 163 20 164 – 167 27 168 – 171 15 172 – 175 12 J u m l a h 100 Tabel frekuensi kumulatip Tepi Bawah Kelas (cm) FK “ ≥ “ ≥ 151,5 100 ≥ 155,5 90 ≥ 159,5 74 ≥ 163,5 54 ≥ 167,5 27 ≥ 171’5 12 0≥ 175’5 next Ogif Negatip T Badan Fk “ ≥ “ 151,5 155,5 159,5 163,5 167,5 171,5 175,5 10 20 30 40 50 60 70 80 90 100 next next 74 54 27
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 e. Membuat Tabel Distribusi Frekuensi dari Data Mentah 1) Tabel Distribusi Frekuensi Data tunggal Berikut ini adalah data nilai matematika 40 siswa kelas XI IPS SMA Negeri 1 Kotabumi (Data Mentah) : next next 3 6 4 9 4 6 8 5 6 7 5 4 3 8 6 3 6 9 7 5 9 5 6 7 6 7 5 7 8 6 6 8 9 6 4 6 6 7 7 8 Data di atas dapat disajikan dalam bentuk tabel distribusi frekuensi data tunggal sebagai berikut : next next NILAI TURUS FREKUENSI 3 4 5 6 7 8 9 JUMLAH III 3 IIII 4 IIIII 5 IIIIIIIIIIII 12 IIIIIII 7 IIIII 5 IIII 4 40 next
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 next 2) Tabel Distribusi Frekuensi Data Berkelompok Berikut ini adalah nilai matematika 60 siswa kelas XI IPS SMA Negeri 1 Kotabumi (Data Mentah) : next 30 35 40 90 42 60 87 55 63 77 56 44 32 85 62 39 61 90 72 55 94 58 68 74 69 75 53 74 89 65 65 82 91 38 46 65 68 76 82 83 67 87 71 70 69 41 45 78 84 35 44 55 66 77 88 71 68 83 69 65 next Data mentah di atas dapat disajikan dalam bentuk tabel distribusi frekuensi data Berkelompok. Berikut adalah pedoman membuat tabel distribusi data berkelompok : 1. Menentukan Rentang atau jankauan data (R), yaitu selisih positip dari nilai data terendah (X1) dan nilai data tertinggi (Xn). RUMUS : R = Xn – X1 next Untuk data di atas : Nilai data terendah (X1) = 30 Nilai data tertinggi (X60) = 94 jadi Rentang : R = X60 – X1 = 94 – 30 = 64 next
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 next 2. Menentukan Banyaknya Kelas Interval ( K ) Bayaknya kelas interval disarankan antara 5 dan 15 kelas, dan sebagai ancer-ancer bisa digunakan aturan Sturges yaitu : Banyak kelas Interval (K) = 1 + 3,3 log n, n = banyaknya niali data nextUntuk data di atas : n = 60 Banyak kelas Interval (K) = 1 + 3,3 log 60 = 1 + 3,3 (1,778) = 1 + 5,867 = 6,867 = 7 ( dibulatkan ) next 3. Menentukan Panjang atau Lebar Kelas Interval (P) Panjang kelas Interval ( P ) dapat ditentukan dengan rumus : Panjang Kelas Interval ( P ) = R dibagi K = R : K next Untuk data di atas : R = 64 , K = 7 Panjang Kelas Interval ( P ) = R : K = 64 : 7 = 9,14 = 10 ( Dibulatkan ke atas ) next 4. Menyusun Tabel Distribusi Frekuensi Data Berkelompok Batas bawah kelas Interval pertama dapat diambil nilai data yang terkecil atau nilai yang lebih kecil dari nilai data terkecil tapi selisihnya tdak lebih dari panjang kelas interval. Sebagai berikut : next
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 next next 30 35 40 90 42 60 87 55 63 77 56 44 32 85 62 39 61 90 72 55 94 58 68 74 69 75 53 74 59 65 65 82 91 38 46 65 68 76 82 83 67 87 71 70 69 41 45 78 84 35 44 55 66 77 88 71 68 53 69 65 Untuk Menyusun Tabel Distribusi Frekuensi Data Berkelompok maka kita harus perhatikan kembali data mentahnya, sebagai berikut : Tabel Distribusi Frekuensi Data Berkelompok KELAS INTERVAL TURUS FREKUENSI 30 – 39 40 – 49 50 – 59 60 – 69 70 – 79 80 – 89 90 – 99 JUMLAH IIIIII 6 IIIIIII 7 IIIIIIII 8 IIIIIIIIIIIIIII 16 IIIIIIIIIII 11 IIIIIIII 8 IIII 4 60 next
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 next Silahkan anda mencoba menyelesaikan soal-soal yang tersedia pada buku literatur anda !
*PEMBELAJARAN MATEMATIKA KLS XI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 next next

More Related Content

PDF
SOAL UTS MO II tahun 2014
byLilia Pascariani
 
PPT
Analisis Sensitivitas (Analisis Proyek BAB 4)
byBagus Cahyo Jaya Pratama Pratama
 
DOCX
Makalah tentang pengangguran di indonesia
byvinaamelia12
 
DOC
Paragraf deduktif dan induktif dalam artikel koran
byYayu Ferdian
 
PPTX
keputusan dalam keadaan risiko
byAbu Tholib
 
DOC
Bab i sampai 3
byOscar Cole
 
PPT
Kutipan dan daftar pustaka
byMerlinda Ambinari
 
DOCX
Cara Menulis Kutipan dan Daftar Pustaka Karya Tulis Ilmiah
byDedi Irawan
 
SOAL UTS MO II tahun 2014
byLilia Pascariani
 
Analisis Sensitivitas (Analisis Proyek BAB 4)
byBagus Cahyo Jaya Pratama Pratama
 
Makalah tentang pengangguran di indonesia
byvinaamelia12
 
Paragraf deduktif dan induktif dalam artikel koran
byYayu Ferdian
 
keputusan dalam keadaan risiko
byAbu Tholib
 
Bab i sampai 3
byOscar Cole
 
Kutipan dan daftar pustaka
byMerlinda Ambinari
 
Cara Menulis Kutipan dan Daftar Pustaka Karya Tulis Ilmiah
byDedi Irawan
 

What's hot

PPTX
Ppt proposal
byMohammad Mukhlis
 
PDF
Teori tentang low vision
bypendekar ilmu
 
PDF
Anggaran Negara dalam Era Otonomi Daerah
byDadang Solihin
 
PDF
SWOT Pt Tlkom.pdf
byBommberGiray
 
PDF
Presentasi Listrik Tenaga Surya
byPT. Hexamitra Daya Prima
 
PDF
Panduan penulisan PROPOSAL, JURNAL,SKRIPSI UNSRIT 2019
byUNIVERSITAS SARIPUTRA INDONESIA TOMOHON
 
PPT
Sistem proteksi tenaga listrik
byPoliteknik Negeri Ujung Pandang
 
DOC
Contoh perencanaan usaha
byVandy Acdert
 
PPT
Optimalisasi Pajak dan Retribusi Daerah bagi Pembangunan Daerah sesuai UU28/2...
byDadang Solihin
 
PPTX
GARDU DISTRIBUSI
byPoliteknik Negeri Ujung Pandang
 
PDF
Analisis Pengujian Purchasing Power Parity dan International Fisher Effect da...
byTrisnadi Wijaya
 
PDF
Contoh proposal pkm kewirausahaan
byZakiyul Mu'min
 
PPTX
syarat-syarat umum untuk perkembangan ekonomi
byyuniar putri
 
PPTX
Wawasan kemaritiman - Ilmu Pengetahuan dan Teknologi
byIda Bagus Anom Sanjaya
 
DOCX
Makalah PPKN Kasus-kasus pelanggaran hak dan pengingkaran kewajiban warga neg...
byaulia putri
 
DOCX
makalah kebijakan perdagangan internasional (Manajemen Pemasaran)
byendah dwis
 
PDF
DRAF PROPOSAL MAKRAB HIMPUNAN MAHASISWA HOSPITALITY SEKOLAH TINGGI PARIWISATA...
byHimpunan Mahasiswa Hospitality STP AMPTA Yogyakarta
 
DOC
Job desk seminar
bySam Chipmunkz
 
DOCX
9 pertanyaan
bySajuri Cilacap
 
DOC
Modul 8 elastisitas
byDefina Sulastiningtiyas
 
Ppt proposal
byMohammad Mukhlis
 
Teori tentang low vision
bypendekar ilmu
 
Anggaran Negara dalam Era Otonomi Daerah
byDadang Solihin
 
SWOT Pt Tlkom.pdf
byBommberGiray
 
Presentasi Listrik Tenaga Surya
byPT. Hexamitra Daya Prima
 
Panduan penulisan PROPOSAL, JURNAL,SKRIPSI UNSRIT 2019
byUNIVERSITAS SARIPUTRA INDONESIA TOMOHON
 
Sistem proteksi tenaga listrik
byPoliteknik Negeri Ujung Pandang
 
Contoh perencanaan usaha
byVandy Acdert
 
Optimalisasi Pajak dan Retribusi Daerah bagi Pembangunan Daerah sesuai UU28/2...
byDadang Solihin
 
GARDU DISTRIBUSI
byPoliteknik Negeri Ujung Pandang
 
Analisis Pengujian Purchasing Power Parity dan International Fisher Effect da...
byTrisnadi Wijaya
 
Contoh proposal pkm kewirausahaan
byZakiyul Mu'min
 
syarat-syarat umum untuk perkembangan ekonomi
byyuniar putri
 
Wawasan kemaritiman - Ilmu Pengetahuan dan Teknologi
byIda Bagus Anom Sanjaya
 
Makalah PPKN Kasus-kasus pelanggaran hak dan pengingkaran kewajiban warga neg...
byaulia putri
 
makalah kebijakan perdagangan internasional (Manajemen Pemasaran)
byendah dwis
 
DRAF PROPOSAL MAKRAB HIMPUNAN MAHASISWA HOSPITALITY SEKOLAH TINGGI PARIWISATA...
byHimpunan Mahasiswa Hospitality STP AMPTA Yogyakarta
 
Job desk seminar
bySam Chipmunkz
 
9 pertanyaan
bySajuri Cilacap
 
Modul 8 elastisitas
byDefina Sulastiningtiyas
 

Viewers also liked

PPTX
Materi SMA X - Statistika
byAna Sugiyarti
 
PPTX
Statistika Matematika kelas X
byKhansha Hanak
 
PPT
2. Rataan Hitung ( Mean )
bywidi1966
 
PPT
Pertemuan ke 2
byTenia Wahyuningrum
 
PPTX
Penyajian data statistik ppt
byRahmi Farza
 
PPTX
power point statistik by faisal
bymuhammadikhsaniks
 
PPTX
Pert. 3 statistik teknik penarikan sampel
byArief Pratama
 
PPTX
Statistika ppt
byAisyah Turidho
 
PDF
STATISTIKA
byWatowuan Tyno
 
PPT
Statistik Penyajian Data dalam bentuk diagram tabel dan Grafik serta cara pen...
byRifatin Aprilia
 
PPT
Statistika presentation
byMardah Kholida Harahap
 
DOCX
Makalah penyajian data
byAisyah Turidho
 
DOC
Soal dan pembahasan statistika
bysatriyo buaya
 
DOC
Distribusi frekuensi.1
byOst Man
 
PPT
Statistikadanbatang
byWayan Sudiarta
 
PPTX
K3 pelarut organik (pak depkes2005) b
byconny05oktober1992
 
PPT
4. Modus
bywidi1966
 
PPTX
Pengantar statistik
byAinul Fikri
 
PPT
Statistika
byconny05oktober1992
 
DOC
Laporan Metklim Pendidikan Geografi
byJanatun Rahmilah
 
Materi SMA X - Statistika
byAna Sugiyarti
 
Statistika Matematika kelas X
byKhansha Hanak
 
2. Rataan Hitung ( Mean )
bywidi1966
 
Pertemuan ke 2
byTenia Wahyuningrum
 
Penyajian data statistik ppt
byRahmi Farza
 
power point statistik by faisal
bymuhammadikhsaniks
 
Pert. 3 statistik teknik penarikan sampel
byArief Pratama
 
Statistika ppt
byAisyah Turidho
 
STATISTIKA
byWatowuan Tyno
 
Statistik Penyajian Data dalam bentuk diagram tabel dan Grafik serta cara pen...
byRifatin Aprilia
 
Statistika presentation
byMardah Kholida Harahap
 
Makalah penyajian data
byAisyah Turidho
 
Soal dan pembahasan statistika
bysatriyo buaya
 
Distribusi frekuensi.1
byOst Man
 
Statistikadanbatang
byWayan Sudiarta
 
K3 pelarut organik (pak depkes2005) b
byconny05oktober1992
 
4. Modus
bywidi1966
 
Pengantar statistik
byAinul Fikri
 
Statistika
byconny05oktober1992
 
Laporan Metklim Pendidikan Geografi
byJanatun Rahmilah
 

Similar to 1. Penyajian Data Statistik

PPTX
penyajian data matematika kelas 7 sem 2 smp
byAinisAqila1
 
PPTX
PPT Penyajian Data Kelas 7 Semester 2
byKevin Arthur
 
PPTX
ppt_penyajian_data_untuk_smp_kelas_7.pptx
byYogaAhmadi3
 
PPTX
Statistika 1 (penyajian data)
bySigitSurya3
 
PPTX
PPT PENYAJIAN DATA Implementasi Kurikulum Merdeka.pptx
bymtsmaarifpajaresuk24
 
PDF
Statistika Dasar PGSD
bySitiAminahNababan
 
PDF
45567964-Makalah-STATISTIK.pdfkelomppl 1
byhasrilamriawan
 
PDF
Materi Pertemuan 1 ( Populasi dan Sampel)
bycristianpramusinta
 
DOCX
Statistik Diagram
byAii Mandala
 
PPTX
Presentasi Statistika (ukuran pemusatan dan penyebaran))
byEkadionMaulana
 
PPTX
STATISTIKA DASAR MATEMATIKA KELAS 8.pptx
byFarhanPerdanaRamaden1
 
PPTX
statistika SMP.pptx
bymikhawirian
 
PPTX
PENYAJIAN DATA STATISTIK DALM PENELITIAN
byCHAIRULNAZALULANSHAR
 
PPTX
z mtk data dat adat adata dfatatda ya .pptx
byinayahsari83
 
PPTX
STATISTIKA penyajian data ke bentuk diagram .pptx
bytutisolihat0608
 
DOCX
Penyajian data dan aplikasi pada data penelitian
byAYU Hardiyanti
 
DOC
17 statistika
byThytienZaenal
 
DOCX
Materi statistik
bytri cahyani
 
DOCX
Lks 1
byDon't MyName
 
PDF
Statistika kolokium 1
bySepti Maulina Sari
 
penyajian data matematika kelas 7 sem 2 smp
byAinisAqila1
 
PPT Penyajian Data Kelas 7 Semester 2
byKevin Arthur
 
ppt_penyajian_data_untuk_smp_kelas_7.pptx
byYogaAhmadi3
 
Statistika 1 (penyajian data)
bySigitSurya3
 
PPT PENYAJIAN DATA Implementasi Kurikulum Merdeka.pptx
bymtsmaarifpajaresuk24
 
Statistika Dasar PGSD
bySitiAminahNababan
 
45567964-Makalah-STATISTIK.pdfkelomppl 1
byhasrilamriawan
 
Materi Pertemuan 1 ( Populasi dan Sampel)
bycristianpramusinta
 
Statistik Diagram
byAii Mandala
 
Presentasi Statistika (ukuran pemusatan dan penyebaran))
byEkadionMaulana
 
STATISTIKA DASAR MATEMATIKA KELAS 8.pptx
byFarhanPerdanaRamaden1
 
statistika SMP.pptx
bymikhawirian
 
PENYAJIAN DATA STATISTIK DALM PENELITIAN
byCHAIRULNAZALULANSHAR
 
z mtk data dat adat adata dfatatda ya .pptx
byinayahsari83
 
STATISTIKA penyajian data ke bentuk diagram .pptx
bytutisolihat0608
 
Penyajian data dan aplikasi pada data penelitian
byAYU Hardiyanti
 
17 statistika
byThytienZaenal
 
Materi statistik
bytri cahyani
 
Lks 1
byDon't MyName
 
Statistika kolokium 1
bySepti Maulina Sari
 

More from widi1966

DOCX
Soal prediksi un ips paket 2 2013
bywidi1966
 
DOCX
Soal prediksi un ips paket 8 2013
bywidi1966
 
DOCX
Soal prediksi un ipa paket 6 2013
bywidi1966
 
DOC
Soal prediksi un xii ips 2013 paket 13 dan pembahasan
bywidi1966
 
DOCX
Soal prediksi un ips paket 1 2013
bywidi1966
 
DOCX
Soal prediksi un ips paket 4 2013
bywidi1966
 
DOCX
Soal prediksi un ips paket 4 2013
bywidi1966
 
DOCX
Soal prediksi un ips paket 9 2013
bywidi1966
 
DOCX
Soal prediksi un ips paket 5 2013
bywidi1966
 
DOCX
Soal prediksi un ips paket 12 2013
bywidi1966
 
DOCX
Soal prediksi un ips paket 11 2013
bywidi1966
 
DOCX
Soal prediksi un ipa paket 5 2013
bywidi1966
 
DOCX
Soal prediksi un ips paket 3 2013
bywidi1966
 
DOCX
Soal prediksi un ips paket 7 2013
bywidi1966
 
DOCX
Soal prediksi un ipa paket 7 2013
bywidi1966
 
DOCX
Soal prediksi un ips paket 6 2013
bywidi1966
 
DOCX
Soal prediksi un ips paket 10 2013
bywidi1966
 
DOCX
Soal prediksi un ipa paket 8 2013
bywidi1966
 
DOCX
Soal prediksi un ipa paket 9 2013
bywidi1966
 
DOCX
Soal prediksi un ipa paket 10 2013
bywidi1966
 
Soal prediksi un ips paket 2 2013
bywidi1966
 
Soal prediksi un ips paket 8 2013
bywidi1966
 
Soal prediksi un ipa paket 6 2013
bywidi1966
 
Soal prediksi un xii ips 2013 paket 13 dan pembahasan
bywidi1966
 
Soal prediksi un ips paket 1 2013
bywidi1966
 
Soal prediksi un ips paket 4 2013
bywidi1966
 
Soal prediksi un ips paket 4 2013
bywidi1966
 
Soal prediksi un ips paket 9 2013
bywidi1966
 
Soal prediksi un ips paket 5 2013
bywidi1966
 
Soal prediksi un ips paket 12 2013
bywidi1966
 
Soal prediksi un ips paket 11 2013
bywidi1966
 
Soal prediksi un ipa paket 5 2013
bywidi1966
 
Soal prediksi un ips paket 3 2013
bywidi1966
 
Soal prediksi un ips paket 7 2013
bywidi1966
 
Soal prediksi un ipa paket 7 2013
bywidi1966
 
Soal prediksi un ips paket 6 2013
bywidi1966
 
Soal prediksi un ips paket 10 2013
bywidi1966
 
Soal prediksi un ipa paket 8 2013
bywidi1966
 
Soal prediksi un ipa paket 9 2013
bywidi1966
 
Soal prediksi un ipa paket 10 2013
bywidi1966
 

1. Penyajian Data Statistik

  • 1.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clik SELAMAT DATANG DI MEDIA PEMBELAJARAN MATEMATIKA SMA NEGERI 1 KOTABUMI LAMPUNG UTARA BERSAMA WIDI ASMORO. S.Pd TAHUN 2013 DALAM POKOK BAHASAN STATISTIKA KELAS XI IPS
  • 2.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 ClikSTATISTIKA 1. Pengertian Statistik dan Statistika Statistik adalah bilangan – bilangan yang melukiskan suatu keadaan atau persoalan tertentu. Misalnya untuk melukiskan keadaan jumlah penduduk suatu negara setiap tahun dinyatakan dengan bilangan (disebut statistik), banyaknya calon siswa baru yang mendaftar di SMA Negeri 1 Kotabumi tahun pelajaran 2013/2014 melalui jalur tes adalah 542 orang ( 542 disebut statistik ). Dan lain sebagainya. Clik Adapun Statistika berasal dari kata “ Statistik” dan “ logika “ yang dapat diartikan sebagai ilmu statistik, yaitu ilmu yang mempelajari tentang bagai mana cara mengumpulkan data, menyajikan data, mengolah data, menganalisa data dan menarik kesimpulan berdasarkan data yang ada sehingga dapat diambil tindakan atau putusan yang tepat terhadap suatu persolan yang sedang diteliti. Clik 2. Istilah –Istilah Yang Terdapat Dalam Statistika a. Data atau Datum Data adalah bentuk jamak dari “Datum” yang artinya adalah kumpulan keterangan atau imformasi yang diperoleh dari suatu penelitian. Clik
  • 3.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clik Berdasarkan jenisnya data dibedakan menjadi 2 jenis, yaitu data kualitatif dan data kuantitatif. Clik 1) Data kualitatif, yaitu data yang tidak atau bukan bermentuk bilangan, misalnya data tentang mutu hasil panen padi di suatu kabupaten, data tentang mutu barang elektronik di gudang suatu perusahan eleektronik, dan lain sebagainya. Untuk menggambarkan data kualitatif biasanya digunakan kata-kata seperti : “ baik “, “buru”, “rusak” ,dll. Clik2) Data kuantitatif, yaitu data yang berbentu bilangan atau angka. Misalnya data tentang jumlah penduduk di suatu negara, data banyaknya kecelakaan lalu lintas, data tentang suhu badan pasien penyakit tipus. Dll. Clik Data kuantitatif dibedakan menjadi 2 macam, yaitu data diskrit dan data kontinu. Data diskrit adalah data yang diperoleh dari hasil mencacah atau menghitung, misalnya data tentang banyaknya buku yang ada di perpustakan. Data kontinu adalah data yang diperoleh dari hasil pengukuran, misalnya data tentang tinggi badan siswa, data tentang suhu badan pasien, dll. Clik
  • 4.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clikb. Populasi dan Sampel Populasi adalah himpunan atau kumpulan semua objek yang sedang menjadi bhan penelitian atau pengamatan. Sedangkan Sampel adalah bagian dari populasi yang sedang diamati atau diteliti dan dapat mewakili populasi. Clik Sebagai contoh : Dalam sebuah penelitian tentang rata-rata tinggi badan siswa SMA di propinsi Lampung, Maka sebagai populasi adalah semua siswa SMA sepropinsi Lampung sedangkan sampelnya dapat dipilih secara acak sebuah SMA yang ada di propinsi Lampung, mislanya terpilih SMA Negeri 1 kotabumi sebagai sampel, berarti SMA Negeri 1 Kotabumi mewakili populasi.Clik c. Pengumpulan data ada 2 metode dalam pengumpulan data. Yaitu metode sensus dan metode sampling. Sensus adalah metode pengumpulan data dengan meneliti atau mengamati setiap anggota populsi. Sampling adalah metode pengumpulan data dengan meneliti sampel atau sebagian yang mewakili populasi. Clik
  • 5.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clik d. Teknik Pengumpulan Data Ada beberapa teknik pengumpulan data dalam sebuah penelitian, antara lain : 1) interpiew atau wawancara, yaitu suatu teknik pengumpulan data dengan cara bertanya langsung kepada responden face to face tentang informasi yang diperlukan dari daftar pertanyaan yang sudah dipersiapkan sebelimnya. Clik 2) Kuisoner atau angket, yaitu suatu teknik pengumpulan data dengan cara memberi responden daftar pertanyaan yang dicetak dalam selembar atau dua lembar kertas dengan pertanyaan yang sama seperti pada wawancara Clik 3) Obsevasi langsung atau pengamatan langsung, yaitu suatu teknik pengumpulan data dengan cara mengamati objek yang sedang diteliti secara langsung dengan panca indera. Teknik ini biasanya digunakan untuk penelitian yang berkaitan dengan bidang IPA . Misalnya meneliti air sebuah sungai apakah tercemar limbah beracun atau tidak tentu tidak dapat dilakukan dengan wawancara atau angket dalam pengumpulan datanya. Clik
  • 6.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clik2. Menyajikan Data Tunggal dalam Bentuk Tabel dan Diagram Agar mudah pahami orang lain Data statistik yang sudah dikumpulkan biasanya disajikan dalam bentuk tabel atau diagram. Clik a. Diagram Batang Diagram batang adalah diagram berbentuk batang atau balok. Diagram batang biasanya digunakan untuk membandingkan antar nilai data. Diagram batang dapat berbentuk tunggal, majemuk atau bertingkat. Berikut ini contoh-contoh diagram batang : Clik Contoh : Berikut adalah tabel data tentang banyaknya pendaftar PPDB SMA Negeri 1 Kotabumi jalur bakat dan prestasi akademik dari tahun 2007 sampai dengan 2013 TAHUN 2008 2009 2010 2011 2012 2013 LAKI-LAKI PEREMPUAN JUMLAH 300 400 700 200 300 500 250 350 600 300 500 800 250 425 675 300 350 650 Tabel Pendaftar Calon PPDB SMA N 1 Kotabumi Jalur Bakat Dan Prestasi Akademik Tahun 2007 s.d 2013 Clik Clik
  • 7.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 ClikDari data pada tabel di atas, penyajiannya dapat di ubah ke berbagai macam diagram batang. Sebagai berikut : Diagram Batang Tegak Pendaftar Calon PPDB SMA N 1 Kotabumi Jalur Bakat Dan Prestasi Akademik Tahun 2007 s.d 2013 Clik Tahun Jumlah Clik 2008 2009 2010 2011 2012 2013 100 200 300 400 500 600 700 800 Clik Clik
  • 8.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clik Diagram Batang Mendatar Pendaftar Calon PPDB SMA N 1 Kotabumi Jalur Bakat Dan Prestasi Akademik Tahun 2007 s.d 2013 Clik Jumlah Tahun Clik 100 200 300 400 500 600 2008 2009 2010 2011 2012 2013 Clik Clik 700 800
  • 9.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clik Diagram Batang Majemuk Pendaftar Calon PPDB SMA N 1 Kotabumi Jalur Bakat Dan Prestasi Akademik Tahun 2007 s.d 2013 Clik Tahun Jumlah Clik 2008 2009 2010 2011 2012 2013 50 100 150 200 250 300 350 400 Clik Clik 450 500 Ket: Laki-laki perempuan
  • 10.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clik Clik Diagram Batang Bersusun Pendaftar Calon PPDB SMA N 1 Kotabumi Jalur Bakat Dan Prestasi Akademik Tahun 2007 s.d 2013 Tahun Jumlah 2008 2009 2010 2011 2012 2013 100 200 300 400 500 600 700 800 Ket : Laki-laki perempuan
  • 11.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clikb. Diagram Garis Diagram garis atau grafik adalah diagram berbentuk garis. Diagram garis biasanya digunakan untuk menyajikan data yang diperoleh dari berdasarkan pengamatan dari waktu ke waktu secara berurutan : Clik Contoh : Berikut adalah tabel data tentang banyaknya pendaftar PPDB SMA Negeri 1 Kotabumi jalur bakat dan prestasi akademik dari tahun 2007 sampai dengan 2013 TAHUN 2008 2009 2010 2011 2012 2013 LAKI-LAKI PEREMPUAN JUMLAH 300 400 700 200 300 500 250 350 600 300 500 800 250 425 675 300 350 650 Tabel Pendaftar Calon PPDB SMA N 1 Kotabumi Jalur Bakat Dan Prestasi Akademik Tahun 2007 s.d 2013 Clik Data pada tabel di atas dapat disajikan dalam bentuk diagram garis, sebagai berikut :
  • 12.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 ClikDiagram Garis Pendaftar Calon PPDB SMA N 1 Kotabumi Jalur Bakat Dan Prestasi Akademik Tahun 2007 s.d 2013 Clik Tahun Jumlah 2008 2009 2010 2011 2012 2013 100 200 300 400 500 600 700 800 Clik Laki-laki Clik Perempuan Jumlah Total Clik
  • 13.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clikc. Diagram Lingkaran Diagram lingkaran adalah diagram berbentuk daerah lingkaran. Daerah lingkaran dibagi dalam juring-juring lingkaran. Luas setiap juring lingkaran biasanya dinyatakan dalam persen : Clik Contoh : Data mata pencaharian 300 penduduk desa Subur pada tahun 2010 ditunjukan pada tabel berikut : Mt Pencaharian frekuensi petani petambak pedagangguru karyawan jumlah 90 25 50 105 30 300 Clik Untuk membuat diagram lingkaran dari data pada tabel di atas , perlu kita lakukan langkah berikut : Mata Pencaharian petani petambak guru pedagang karyawan Besar sudut pusat juring persentase 90 /300 x 3600 = 1080 25 /300 x 3600 = 300 50 /300 x 3600 = 600 105 /300 x 3600 = 1260 30 /300 x 3600 = 360 90 /300 x 100% = 30% 25 /300 x 100% = 8,33% 50 /300 x 100% = 16,67% 105 /300 x 100% = 35% 30 /300 x 100% = 10% Clik
  • 14.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clik Diagram Lingkaran Data Mata Pencaharian 300 Penduduk Desa Subur pada Tahun 2010 108 0 30 % Clik PETAN I P ETA M B A K 8 ,3 3 % GURU 16,67 % Clik 126 0 PEDAGAN G 35% 360 KARYAWAN 10% Clik 600
  • 15.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 Clik3. Membaca dan Menyajikan Data kelompok dalam Bentuk Tabel dan Diagram Data kelompok merupakan data yang ditulis dalam suatu interval. Data kelompok sering digunakan untuk menyajikan data dalam jumlah banyak ( besar ). Clik a. Tabel atau Daftar distribusi Frekuensi Data Kelompok Berikut ini contoh tabel distribusi frekuensi data berkelompok. ClikData Tinggi Badan 100 Siswa kelas XI SMA Negeri 1 Kotabumi TP 2011/2012 Clik Tinggi Badan (cm) Frekuensi 152 – 155 10 156 – 159 16 160 – 163 20 164 – 167 27 168 – 171 15 172 – 175 12 J u m l a h 100
  • 16.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 next b. Beberapa istilah yang terdapat dalam tabel distribusi frekuensi data berkelompok. Tinggi Badan (cm) Frekuensi 152 – 155 10 156 – 159 16 160 – 163 20 164 – 167 27 168 – 171 15 172 – 175 12 J u m l a h 100 next 1) Kelas Interval , yaitu nilai data yang ditulis dalam bentuk interval. Contoh pada daftar di atas : 152 – 155 Kelas interval ke – 1 156 – 159 Kelas interval ke – 2 160 – 163 Kelas interval ke – 3 172 – 175 Kelas interval ke – 7 next
  • 17.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 next 2) Batas Bawah Kelas Interval , yaitu nilai data yang terletak disebelah kiri setiap kelas interval. Contoh pada daftar di atas : 152 Batas Bawah Kelas interval ke – 1 156 Batas Bawah Kelas interval ke – 2 160 Batas Bawah Kelas interval ke – 3 172 Batas Bawah Kelas interval ke – 7 next 3) Batas Atas Kelas Interval , yaitu nilai data yang terletak disebelah kanan setiap kelas interval. Contoh pada daftar di atas : 155 Batas Atas Kelas interval ke – 1 159 Batas Atas Kelas interval ke – 2 163 Batas Atas Kelas interval ke – 3 175 Batas Atas Kelas interval ke – 7 next 4) Tepi Bawah Kelas Interval , yaitu nilai yang diperoleh dari batas bawah dikurangi 0,5 pada setiap kelas interval. Contoh pada daftar di atas : 152 – 0,5 = 151,5 Tepi Bawah Kelas interval ke – 1 156 – 0,5 = 155,5 Tepi Bawah Kelas interval ke – 2 172 – 0,5 = 171,5 Tepi Bawah Kelas interval ke – 7 next
  • 18.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 next 5) Tepi Atas Kelas Interval , yaitu nilai yang diperoleh dari batas atas ditambah 0,5 pada setiap kelas interval. Contoh pada daftar di atas : 155 + 0,5 = 155,5 Tepi Atas Kelas interval ke – 1 159 + 0,5 = 159,5 Tepi Atas Kelas interval ke – 2 175 + 0,5 = 175,5 Tepi Atas Kelas interval ke – 7 next 6) Titik Tengah Kelas Interval , yaitu nilai yang diperoleh dari setengah kali jumlah batas bawah dan batas atas kelas interval. Contoh pada daftar di atas : ½(152 + 155) = 153,5 Titik Tengah Kelas interval ke – 1 ½(156 + 159) = 157,5 Titik Tengah Kelas interval ke – 2 ½(172 + 175) = 173,5 Titik Tengah Kelas interval ke – 7 next 7) Panjang Kelas atau Lebar Kelas , yaitu nilai yang diperoleh dari selisih positip tepi bawah dan tepi atas kelas interval. Contoh pada daftar di atas : 155,5 – 151,5 = 4 Titik Tengah Kelas interval ke – 1 159,5 – 155,5 = 4 Titik Tengah Kelas interval ke – 2 175,5 – 171,5 = 4 Titik Tengah Kelas interval ke – 7 next
  • 19.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 nextc. Histogram dan Poligon Frekuensi Dari tabel distribusi frekuensi data berkelompok dapat dibuat diagram yang bernama Histogram. Histogram adalah diagram yang berupa batang – batang atau persegipanjang – persegipanjang tegak yang saling berimpit. Lebar persegipanjang sebanding dengan lebar kelas dan tinggi persegipanjang sebanding dengan besar frekuesi kelas interval masing – masing. Sedangkan Poligon Frekuensi adalah garis patah – patah yang menghubungkan titik tengah – titik tengah sisi atas histogram. next Sebagai contoh, kita akan buat histogram dan poligon frekuensi dari data pada tabel distribusi frekuensi berkelompok berikut ini : Tinggi Badan (cm) Frekuensi 152 – 155 10 156 – 159 16 160 – 163 20 164 – 167 27 168 – 171 15 172 – 175 12 J u m l a h 100 next
  • 20.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 nextPerhatikan cara membuat histogram dan poligon frekuensi dari data pada tabel distribusi frekuensi berkelompok berikut ini : Histogram dan Poligon Frekuensi Tinggi Badan (cm) Banyak Siswa/ Frekuensi 151,5 155,5 159,5 163,5 167,5 171,5 175,5 4 8 12 16 20 24 28 next Histogram next Poligon Frekuensi next
  • 21.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 next d. Frekuensi Kumulatif dan Ogif 1) Frekuensi Kumulatif kurang Dari dan Ogif Positip Frekuensi kumulatif kurang dari ( fk ≤ ) adalah jumlah frekuensi yang memiliki nilai kurang dari atau sama dengan nilai tepi atas suatu kelas interval. Dari tabel distribusi frekuensi kumulatif kurang dari dapat dibuat sebuah kurva mulus yang disebut Ogif Positip. nextContoh : Membuat tabel distribusi Frekuensi Kumulatif kurang Dari dan Ogif Positip dari tabel distribusi frekuensi berkelompok berikut ini. Tinggi Badan (cm) Frekuensi 152 – 155 10 156 – 159 16 160 – 163 20 164 – 167 27 168 – 171 15 172 – 175 12 J u m l a h 100 next
  • 22.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 nextPenyelesaian : Tinggi Badan (cm) Frekuensi 152 – 155 10 156 – 159 16 160 – 163 20 164 – 167 27 168 – 171 15 172 – 175 12 J u m l a h 100 Tabel frekuensi kumulatip Tepi Atas Kelas (cm) FK “≤ “ ≤ 151,5 0 ≤ 155,5 10 ≤ 159,5 26 ≤ 163,5 46 ≤ 167,5 73 ≤ 171’5 88 100≤ 175’5 next Ogif Positip T Badan Fk “ ≤ “ 151,5 155,5 159,5 163,5 167,5 171,5 175,5 10 20 30 40 50 60 70 80 90 100 next next 26 46 73 88
  • 23.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 next 2) Frekuensi Kumulatif Lebih Dari dan Ogif Negatif Frekuensi kumulatif kurang dari ( fk ≥ ) adalah jumlah frekuensi yang memiliki nilai lebih dari atau sama dengan nilai tepi bawah suatu kelas interval. Dari tabel distribusi frekuensi kumulatif lebih dari dapat dibuat sebuah kurva mulus yang disebut Ogif Negatip. next Contoh : Membuat tabel distribusi Frekuensi Kumulatif lebih Dari dan Ogif negatip dari tabel distribusi frekuensi berkelompok berikut ini. Tinggi Badan (cm) Frekuensi 152 – 155 10 156 – 159 16 160 – 163 20 164 – 167 27 168 – 171 15 172 – 175 12 J u m l a h 100 next
  • 24.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 nextPenyelesaian : Tinggi Badan (cm) Frekuensi 152 – 155 10 156 – 159 16 160 – 163 20 164 – 167 27 168 – 171 15 172 – 175 12 J u m l a h 100 Tabel frekuensi kumulatip Tepi Bawah Kelas (cm) FK “ ≥ “ ≥ 151,5 100 ≥ 155,5 90 ≥ 159,5 74 ≥ 163,5 54 ≥ 167,5 27 ≥ 171’5 12 0≥ 175’5 next Ogif Negatip T Badan Fk “ ≥ “ 151,5 155,5 159,5 163,5 167,5 171,5 175,5 10 20 30 40 50 60 70 80 90 100 next next 74 54 27
  • 25.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 e. Membuat Tabel Distribusi Frekuensi dari Data Mentah 1) Tabel Distribusi Frekuensi Data tunggal Berikut ini adalah data nilai matematika 40 siswa kelas XI IPS SMA Negeri 1 Kotabumi (Data Mentah) : next next 3 6 4 9 4 6 8 5 6 7 5 4 3 8 6 3 6 9 7 5 9 5 6 7 6 7 5 7 8 6 6 8 9 6 4 6 6 7 7 8 Data di atas dapat disajikan dalam bentuk tabel distribusi frekuensi data tunggal sebagai berikut : next next NILAI TURUS FREKUENSI 3 4 5 6 7 8 9 JUMLAH III 3 IIII 4 IIIII 5 IIIIIIIIIIII 12 IIIIIII 7 IIIII 5 IIII 4 40 next
  • 26.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 next 2) Tabel Distribusi Frekuensi Data Berkelompok Berikut ini adalah nilai matematika 60 siswa kelas XI IPS SMA Negeri 1 Kotabumi (Data Mentah) : next 30 35 40 90 42 60 87 55 63 77 56 44 32 85 62 39 61 90 72 55 94 58 68 74 69 75 53 74 89 65 65 82 91 38 46 65 68 76 82 83 67 87 71 70 69 41 45 78 84 35 44 55 66 77 88 71 68 83 69 65 next Data mentah di atas dapat disajikan dalam bentuk tabel distribusi frekuensi data Berkelompok. Berikut adalah pedoman membuat tabel distribusi data berkelompok : 1. Menentukan Rentang atau jankauan data (R), yaitu selisih positip dari nilai data terendah (X1) dan nilai data tertinggi (Xn). RUMUS : R = Xn – X1 next Untuk data di atas : Nilai data terendah (X1) = 30 Nilai data tertinggi (X60) = 94 jadi Rentang : R = X60 – X1 = 94 – 30 = 64 next
  • 27.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 next 2. Menentukan Banyaknya Kelas Interval ( K ) Bayaknya kelas interval disarankan antara 5 dan 15 kelas, dan sebagai ancer-ancer bisa digunakan aturan Sturges yaitu : Banyak kelas Interval (K) = 1 + 3,3 log n, n = banyaknya niali data nextUntuk data di atas : n = 60 Banyak kelas Interval (K) = 1 + 3,3 log 60 = 1 + 3,3 (1,778) = 1 + 5,867 = 6,867 = 7 ( dibulatkan ) next 3. Menentukan Panjang atau Lebar Kelas Interval (P) Panjang kelas Interval ( P ) dapat ditentukan dengan rumus : Panjang Kelas Interval ( P ) = R dibagi K = R : K next Untuk data di atas : R = 64 , K = 7 Panjang Kelas Interval ( P ) = R : K = 64 : 7 = 9,14 = 10 ( Dibulatkan ke atas ) next 4. Menyusun Tabel Distribusi Frekuensi Data Berkelompok Batas bawah kelas Interval pertama dapat diambil nilai data yang terkecil atau nilai yang lebih kecil dari nilai data terkecil tapi selisihnya tdak lebih dari panjang kelas interval. Sebagai berikut : next
  • 28.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 next next 30 35 40 90 42 60 87 55 63 77 56 44 32 85 62 39 61 90 72 55 94 58 68 74 69 75 53 74 59 65 65 82 91 38 46 65 68 76 82 83 67 87 71 70 69 41 45 78 84 35 44 55 66 77 88 71 68 53 69 65 Untuk Menyusun Tabel Distribusi Frekuensi Data Berkelompok maka kita harus perhatikan kembali data mentahnya, sebagai berikut : Tabel Distribusi Frekuensi Data Berkelompok KELAS INTERVAL TURUS FREKUENSI 30 – 39 40 – 49 50 – 59 60 – 69 70 – 79 80 – 89 90 – 99 JUMLAH IIIIII 6 IIIIIII 7 IIIIIIII 8 IIIIIIIIIIIIIII 16 IIIIIIIIIII 11 IIIIIIII 8 IIII 4 60 next
  • 29.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 next Silahkan anda mencoba menyelesaikan soal-soal yang tersedia pada buku literatur anda !
  • 30.
    *PEMBELAJARAN MATEMATIKA KLSXI IPS SMA NEGERI 1 KOTABUMI BY WIDI ASMORO TAHUN 2013 next next