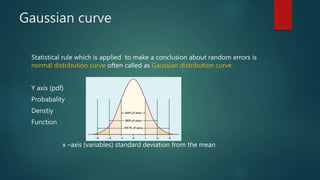
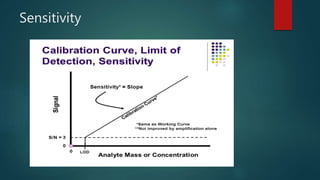
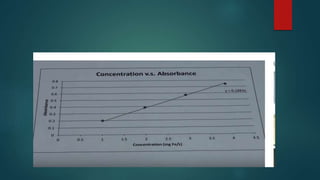
This document discusses statistical analysis and errors in measurement. It defines statistical analysis as dealing with numerical data using probability theory. Measurement errors can be divided into determinate (systematic) errors and indeterminate (random) errors. Determinate errors can be avoided or corrected, while indeterminate errors cannot be determined precisely but their probability can be estimated using statistical distributions like the Gaussian curve. The document also discusses concepts like significant figures, rounding off data, measures of central tendency (mean, median, mode), standard deviation, tests like F-test and T-test, quality control/quality assurance, good laboratory practices, validation of analytical methods and their parameters.

1. Statistical analysis &
errors

2. What is statistical analysis ?
The science that deals with the collection, analysis, and interpret
ation of numerical data, often using probability theory.
 The data themselves
 In data there is always errors due to human and instrumental
errors some can be corrected and avoided but some can not
because they are inderminate

3. Determinate Errors—They Are
Systematic
Determinate or systematic errors are
nonrandom and occur when something is
intrinsically wrong in the measurement.
They can be avoided or corrected

4.  Measurements errors can be divided into two
components
 Non random errors
 Systematic errors

5.  Non Random error
 They have slight order.
 Systematic error
 repeatable error associated with faulty equipment or a flawed
experiment design. These errors are usually caused by
measuring instruments that are incorrectly calibrated or are
used incorrectly.

6.  Determinate errors (systematic errors) are those that, as the name implies,
are determinable means they can be corrected or avoided.
 1) Mis-calibration of apparatus. This can be removed by checking the
apparatus against a standard.
 (2) Faulty observation. This is avoidable, and therefore should not be cited
as a source of error in any well-performed experiment.

7.  The error can be proportional to sample size or may change in a more
complex manner
 Variation are usually unidirectional
 As in the case of solubility loss of precipitate due to its solubility . Such an
example is the change in solution volume and concentration occurring
with changes in temperature. This can be corrected for by measuring the
solution temperature. Such measurable determinate errors are classed as
systematic errors.

8. Inderminate errors or random errors
 Inderminate errors are always random errors and can not be avoided
 Random errors ( inderminate)
It is caused by inherently unpredictable
fluctuations in the readings of a
measurement apparatus or in the
experimenter's interpretation of the
instrumental reading.

9.  Random errors are often called as accidental error.
 Random errors are indeterminate which means they
can not be determined/ calculated. But, we can make
a certain conclusion about these random errors by
applying mathematical more precisely statistical rules.

10. Gaussian curve
Statistical rule which is applied to make a conclusion about random errors is
normal distribution curve often called as Gaussian distribution curve.
Y axis (pdf)
Probabality
Denstiy
Function
x –axis (variables) standard deviation from the mean

11. Significant figures
 Definition
 the number of digits necessary to express the results of a measurement
consistent with the measured precision.
 Since there is uncertainty in any measurement of atleast +_ 1 in the last
significant figures.
 Rules
 Non-zero digits are always significant.
 Any zeros between two significant digits are significant.
 Zeros on the left side are always non-significant while zeros on right side
always significant.

12. For example
 0.216 Three significant figures
 90.7 Three significant figures
 800.0 Four significant figures
 0.0670 Three significant figures

13. Rounding off data
 Definition.
 Rounding off is a kind of estimating. To round off
decimals: Find the place value you want (the
"rounding digit") and look at the digit just to the
right of it. If that digit is less than 5, do not change
the rounding digit but drop all digits to the right of it.
For example
 4.7892 rounding of data into two decimal = 4.8

14. Mean, Median, Mode
Mean.
The sum of a group of measurements divided by the number of
measurements; the average.
Mode.
The most frequently occurring value in the group of
measurement.
2, 3, 4, 2, 5, 2, 7, 5, 2 so 2 is mode in it
Median.
In a even data set, the median is the average of two middle
numbers.
2, 4, 6,8,10 then 6 is median here

15. What is standard deviation
 For a series of ‘n’ measurement of the same measurand, the quantity S
characterizing dispersion of results

 X= measutrements
 X = mean
 N= numbers

16. Tests
 F-test:
 is used to determinate when two variances are satisfactorily different from
each other .
F= S / S2
T-test
Is used to determinate when two sets are satisfactorily different.
Q-test
Is used to determine when outlier is due to determinate error. If it is not , then
falls within expected random error and should be retained.

17. QC/QA
 A good laboratory practice (GLP) means who is defining for and what
purpose. A good laboratory should have
 Management
 Personnel
 Facilities
 Equipment
 Operation
 Method validation
 Quality assurance

18.  Good laboratory practices have been established by
worldwide bodies such as the Organization for
Economic Cooperation and Development (OECD)
and the International Organization for
Standardization (ISO). Government agencies have
adopted them for their purposes as rules that must
be followed for laboratories involved in analyzing
substances that require regulation. Examples are
pharmaceutical formulations, foods, and
environmentally important samples.

19. GLPs
 GLPs ( good laboratory practice) a body of rules, operating
procedures, and practices established by a given organization
that are considered to be mandatory with a view to ensuring
quality and correctness in the results produced by a
laboratory.
 GLP ensures correct results are reported.

20.  The laboratory should have two things
 1. SOPs ( standard operating procedures)
 2. QAU (quality assurance unit)

21. SOPs
 Standard operating procedures provide detailed
descriptions of activities performed by the laboratory.
 1) sample custody chain
 2)sample handling and preparation
 3) the analytical method
 4) instrument maintenance
 5) record keeping

22. QAU (quality assurance unit)
 The QAU is responsible for assuring good
laboratory practices are implemented.
Everyone in the lab is responsible for following
them.

23. Validation of analytical methods
 Validation process
 1) selectivity
 2) Linearity
 3) accuracy
 4) Precision
 5) Sensitivity

24.  6) Range
7) Limit of detection (LOD)
 8) Limit of quantitation
 9) Ruggedness or robustness

25. Selectivity
 Selectivity is basically the extent that the method can measure the analyte
of interest in the matrices of sample being analyzed without interference
from the matrix. Matrix effect may be either positive or negative
Matrix
 Matrix is everything in a sample except the actual analyte

26. Linearity

27. Accuracy
Precision

28. Sensitivity

29. The sensitivity is determined by slope of the calibration
curve and generally reflects the ability to distinguish
two different concentrations
You can measure slope or measure sample of closely
related conc. At high, intermediate, and low
concentrations

31. Range
 Range is actually an interval between upper and
lower concentrations of analyte in sample

32. LOD / LOQ

33. Robustness