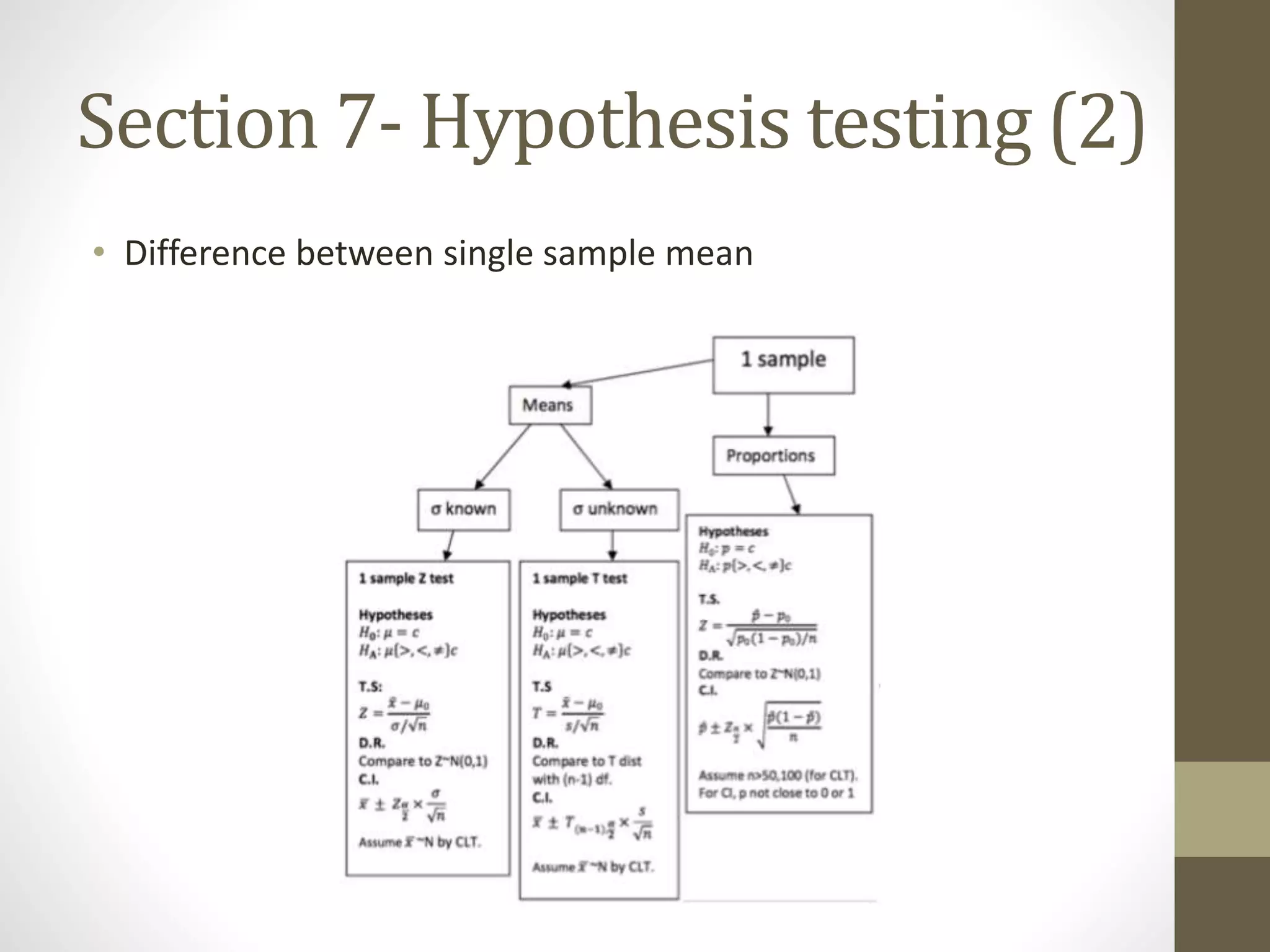
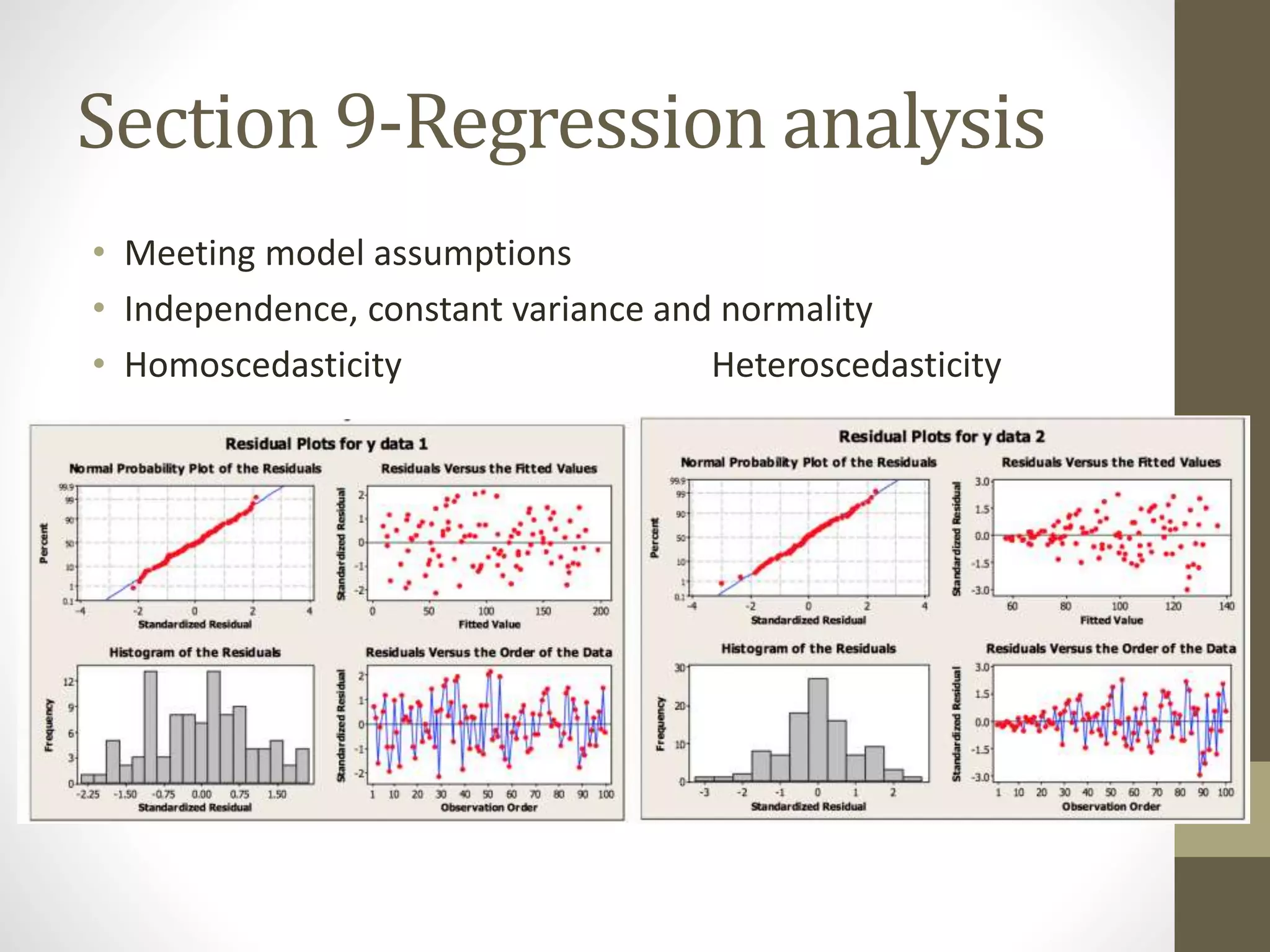
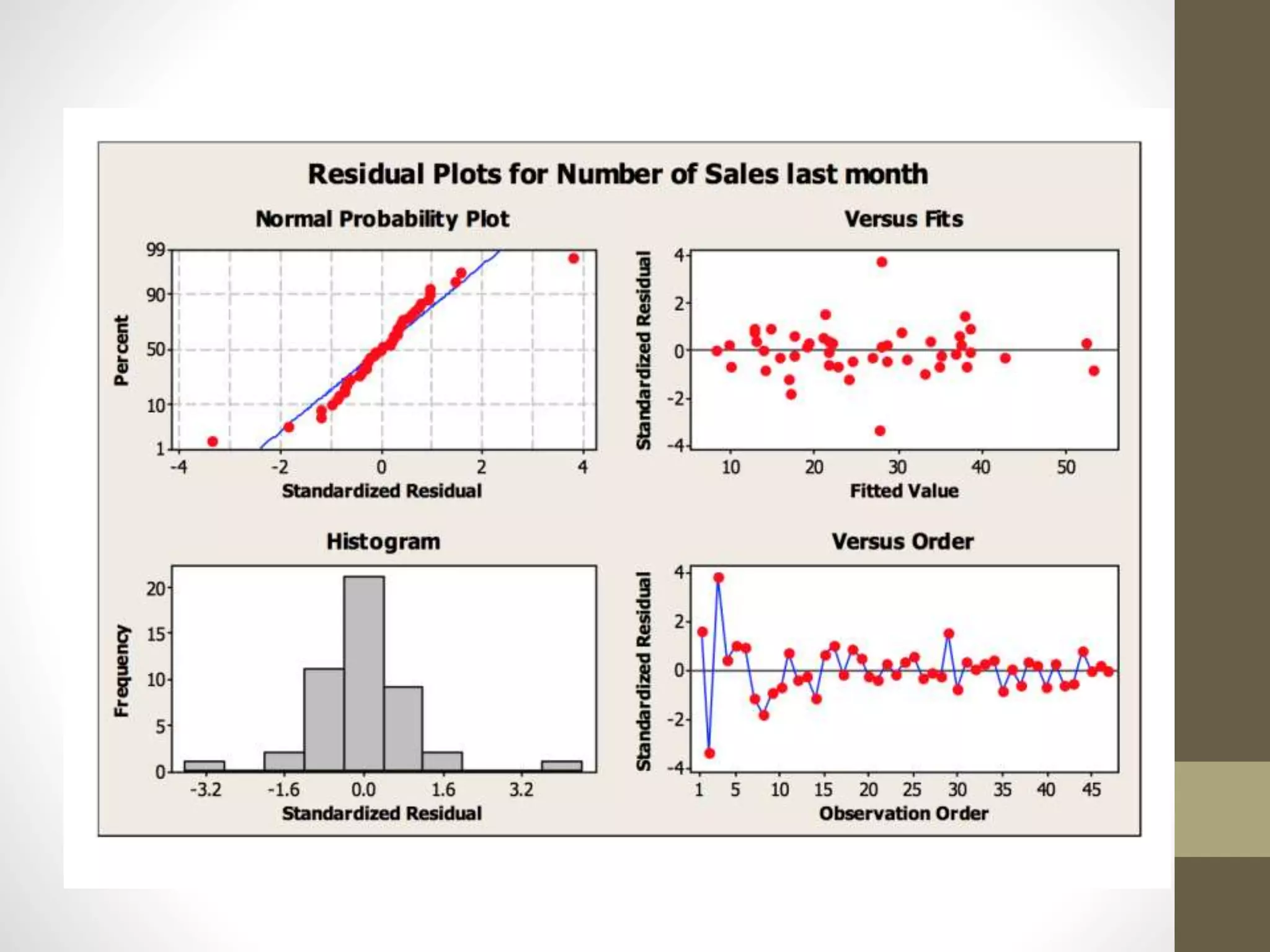
This document provides an overview and examples for a STAT1008 tutorial covering 9 sections: 1) data collection, 2) variables and statistics, 3) probability, 4) continuous probability distributions, 5) sampling distributions, 6) interval estimation, 7) hypothesis testing, 8) hypothesis tests for variances, and 9) regression analysis. Key concepts are explained for each section along with examples from past exams. The tutorial aims to cover the key points needed to understand the material and do well on exams through challenging questions and general hints.

1. STAT1008
TUTORIAL
Jiabin Zhong
u5565270@uds.anu.edu.au

2. Overview
• Key points from each of the sections+ examples for harder
sections
• Example questions from previous exams
• Challenging questions students found hard
• General hints and tips throughout the presentation

3. Section 1-Data collection
• Probability VS non probability sampling
• Comparison of sampling techniques

4. Section 2-Variables, Data and
Statistics
• Mean and Variance
• Covariance and Correlation

5. Section 3-Probability (1)
• Recommend Venn Diagrams when approaching simple
probability questions.
• Key relationships
• (1)
• (2)
• (3)Conditional:
• (4)Independence:
• (5)Multiplication rule:

6. Section 3-Probability (2)
• Rules for expectation: Rules for variance:
Binomial Tables:
• Example: Find P(-2<Z<2)
•

7. Probability examples

8. Section 4- Continuous probability
distributions
• Uniform distribution
• Standardising
• If X is approximately normal with mean μ and variance σ2

9. Uniform problem examples

10. Section 5-Sampling Distributions
• Central Limit Theorem: If X is a random variable with a mean µ
and variance σ²,
• CLT holds for all large samples. E.g.: n ≥ 50.
• REMEMBER: some questions will give variance instead of std.
dev. to mislead you. Be sure to convert.
 
2
,
~ 0,1 as .
X N
n
X
Z N n
n




 
  
 

  

11. Section 6- Interval estimation
• 100(1-α)% Confidence Interval: (Refer to normal tables)
• An alpha of 0.05 means for a repeated sampling , 95% of such
intervals created would contain the true population mean.
/2 /2
/2
100(1 )%
100(1 )% CI:
P x Z x Z
n n
x Z
n
 

 
 


 
      
 
 

12. Section 7- Hypothesis testing (1)
• Two tailed H0= C, HA ≠ C
• One tailed H0=C, HA>C (or HA<C)
• TS (know variance): Compare with Z-Standard normal
distribution
• TS (unknown variance): Compare with t-distribution with n-1
degrees of freedom
• Give appropriate conclusion

13. Section 7- Hypothesis testing (2)
• Difference between single sample mean

14. Two tailed and one tailed
examples- Likely to be on exam

15. Section 8-Hypothesis test (3)
• Same steps as previous slides when conducting a hypothesis
test for two variances.
• 1. Null and Alternative hypothesis
• 2. Test statistic-(Generally put larger sample variance on top)

16. Section 8- Hypothesis test (4)
• 3. Decision rule
• Compare with F-distribution with n-1 numerator and n-1
denominator given the required alpha level.
• Conclusion

17. Section 9-Regression analysis
• Meeting model assumptions
• Independence, constant variance and normality
• Homoscedasticity Heteroscedasticity

18. Section 9-Regression analysis (2)
• Interpretation of ANOVA Table
• Lets go through some examples to see how table works!

19. 2010 Q2 past exam

22. Other questions
• 2013 Q1

23. Good luck for your exam!!!•