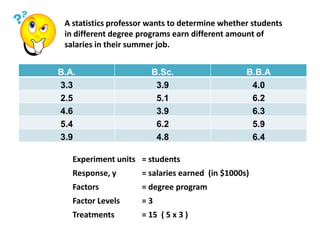
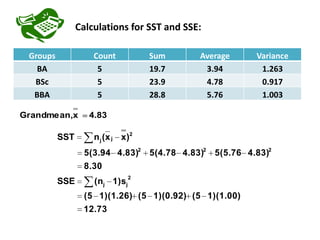
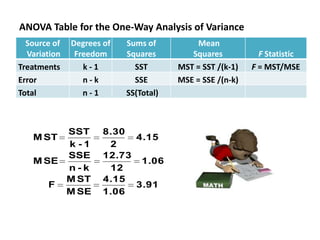
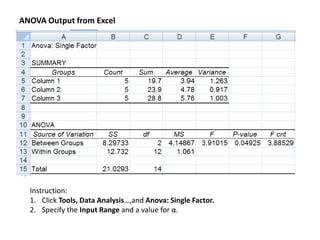
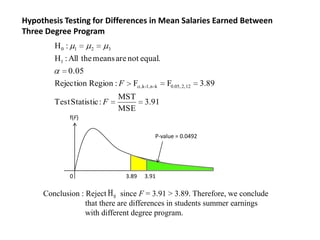
This document provides information about analysis of variance (ANOVA). It begins by explaining why ANOVA is called ANOVA and defines key terms related to experimental design and ANOVA. It then discusses the advantages of using ANOVA, describes three common experimental designs (completely randomized design, randomized block design, and two-factorial design), and provides an example of a completely randomized design (CRD) to compare mean salaries earned by students in different degree programs over the summer. The example calculates sums of squares, conducts an ANOVA test, and concludes that there are statistically significant differences in mean salaries earned between the three degree programs.

2. INTRODUCTION
Why do we call ANOVA instead of ANOME?
Because the procedure works by analyzing the Sample Variance!
ANOVA the statistical procedure for comparing the population means
Design of the the procedure of selecting sample data with the X’s set in
experiment advance/ the planning of the sampling procedure
Experiment the process of collecting sample data
Response Y the (dependent) variable to be measured
Experimental Unit the object upon which the response measurement y is taken
Factors the independent variables, quantitative or qualitative, that are
related to the response variable, Y
Level the value, that is, the setting- assumed by a factor in an
experiment
Treatments the combinations of levels of the factors for which the
response will be observed

3. WHAT is the ADVANTAGE of using ANOVA?
Partition the total sum of squares, which enable us to measure how much
variation is attributable to differences between populations and within
populations
WHAT are the THREE Different Experimental Designs?
1. Completely Randomized Design (One-Way ANOVA)
2. Randomized Block Design (Two-Way ANOVA)
3. Two-Factorial Design
WHAT is CRD?
To compare p treatments is one which the treatments are randomly
assigned to the experimental units. (when the experiments are uniform)
HOW do we IDENTIFY it?
1. Problem objective: Compare 2 or more populations
2. Data type: Interval
3. Experimental Design: Independent samples

4. A statistics professor wants to determine whether students
in different degree programs earn different amount of
salaries in their summer job.
B.A. B.Sc. B.B.A
3.3 3.9 4.0
2.5 5.1 6.2
4.6 3.9 6.3
5.4 6.2 5.9
3.9 4.8 6.4
Experiment units = students
Response, y = salaries earned (in $1000s)
Factors = degree program
Factor Levels =3
Treatments = 15 ( 5 x 3 )

5. Calculations for SST and SSE:
Groups Count Sum Average Variance
BA 5 19.7 3.94 1.263
BSc 5 23.9 4.78 0.917
BBA 5 28.8 5.76 1.003
Grandmean,x 4.83
SST n j ( x j x )2
5(3.94 4.83)2 5(4.78 4.83)2 5(5.76 4.83)2
8.30
2
SSE (nj 1)sj
(5 1)(1.26) (5 1)(0.92) (5 1)(1.00)
12.73

6. ANOVA Table for the One-Way Analysis of Variance
Source of Degrees of Sums of Mean
Variation Freedom Squares Squares F Statistic
Treatments k-1 SST MST = SST /(k-1) F = MST/MSE
Error n-k SSE MSE = SSE /(n-k)
Total n-1 SS(Total)
SST 8.30
M ST 4.15
k-1 2
SSE 12.73
M SE 1.06
n-k 12
M ST 4.15
F 3.91
M SE 1.06

7. ANOVA Output from Excel
Instruction:
1. Click Tools, Data Analysis…,and Anova: Single Factor.
2. Specify the Input Range and a value for α.

8. Hypothesis Testing for Differences in Mean Salaries Earned Between
Three Degree Program
H0 : 1 2 3
H1 : All the means are not equal.
0.05
Rejection Region : F F , k -1, n - k F0.05, 2, 12 3.89
MST
Test Statistic : F 3.91
MSE
f(F)
P-value = 0.0492
0 3.89 3.91
Conclusion : Reject H 0 since F = 3.91 > 3.89. Therefore, we conclude
that there are differences in students summer earnings
with different degree program.