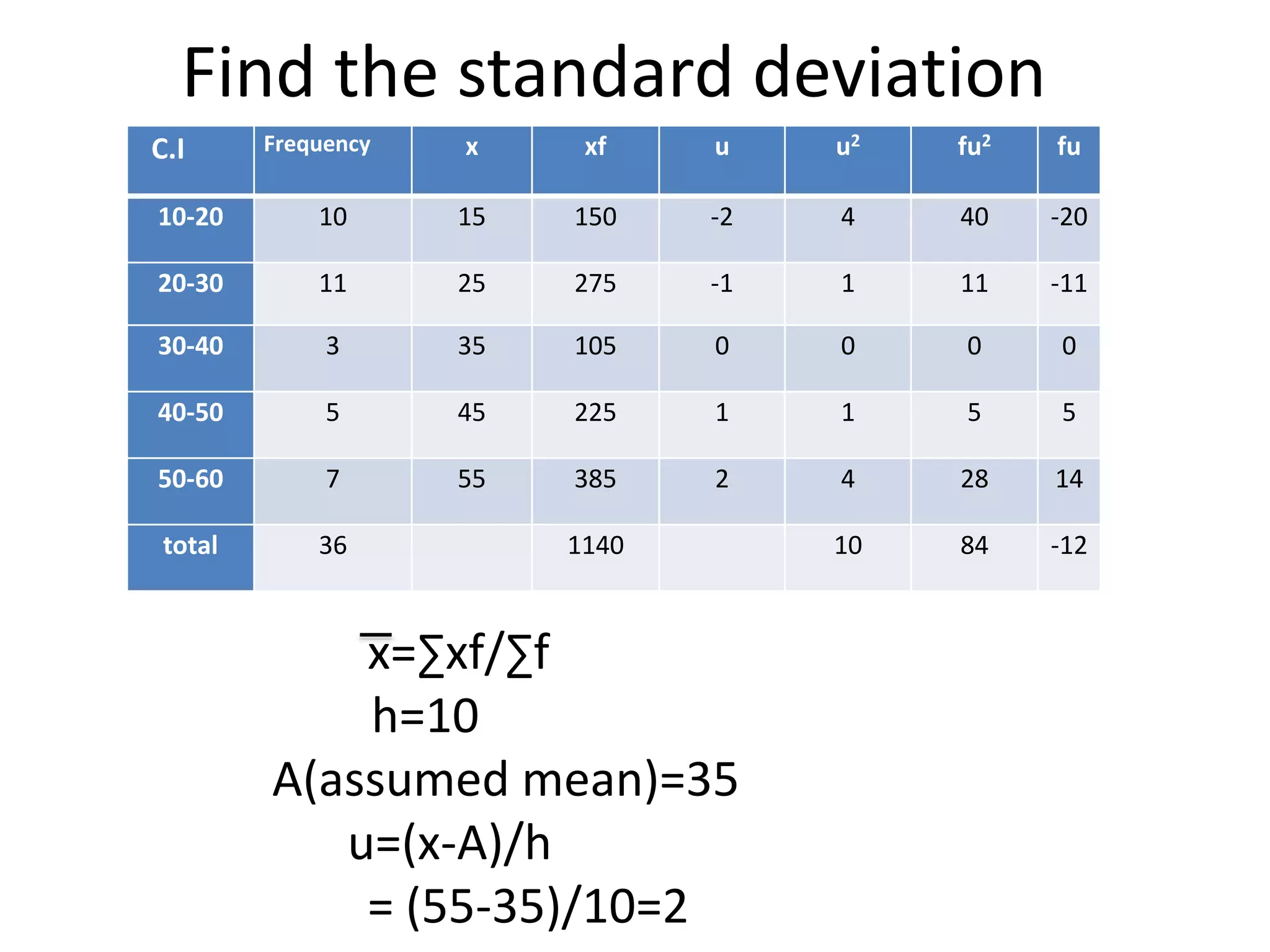
The document defines standard deviation and provides formulas to calculate it from group data. It gives an example of calculating the standard deviation of some sample data with frequency, class intervals, assumed mean, and deviations. The standard deviation is calculated to be 14.90 using the given formula.

1. Standard Deviation
Name : Rahul Sharma
Course: BCA
Subject: Mathematics
Faculty Name : Ms. Megha Sharma

2. Definition
Standard Deviation shows the variation in
data. If the data is close together, the
standard deviation will be small. If the
data is spread out, the standard deviation
will be large.
Standard Deviation is often denoted
by the lowercase Greek letter sigma, .

3. Formulae
For Group Data:
1. S.D( )= [ ∑f(x - x )2/N ]1/2 where N=Sum of frequency
Shortcut Method:
2. =h/N [N∑fu2 –(∑f.u)2 ]1/2 u=x-A/h
3. =[∑(x-x)2/n]1/2 n=no. of observation




4. Find the standard deviation
x=∑xf/∑f
h=10
A(assumed mean)=35
u=(x-A)/h
= (55-35)/10=2
C.I Frequency x xf u u2 fu2 fu
10-20 10 15 150 -2 4 40 -20
20-30 11 25 275 -1 1 11 -11
30-40 3 35 105 0 0 0 0
40-50 5 45 225 1 1 5 5
50-60 7 55 385 2 4 28 14
total 36 1140 10 84 -12

5. =10/36[36(84)-144]1/2
=10/36[3024-144]1/2
=10/36[2880]1/2
=10/36*53.66=14.90
 =h/N [N∑fu2 –(∑f.u)2 ]1/2