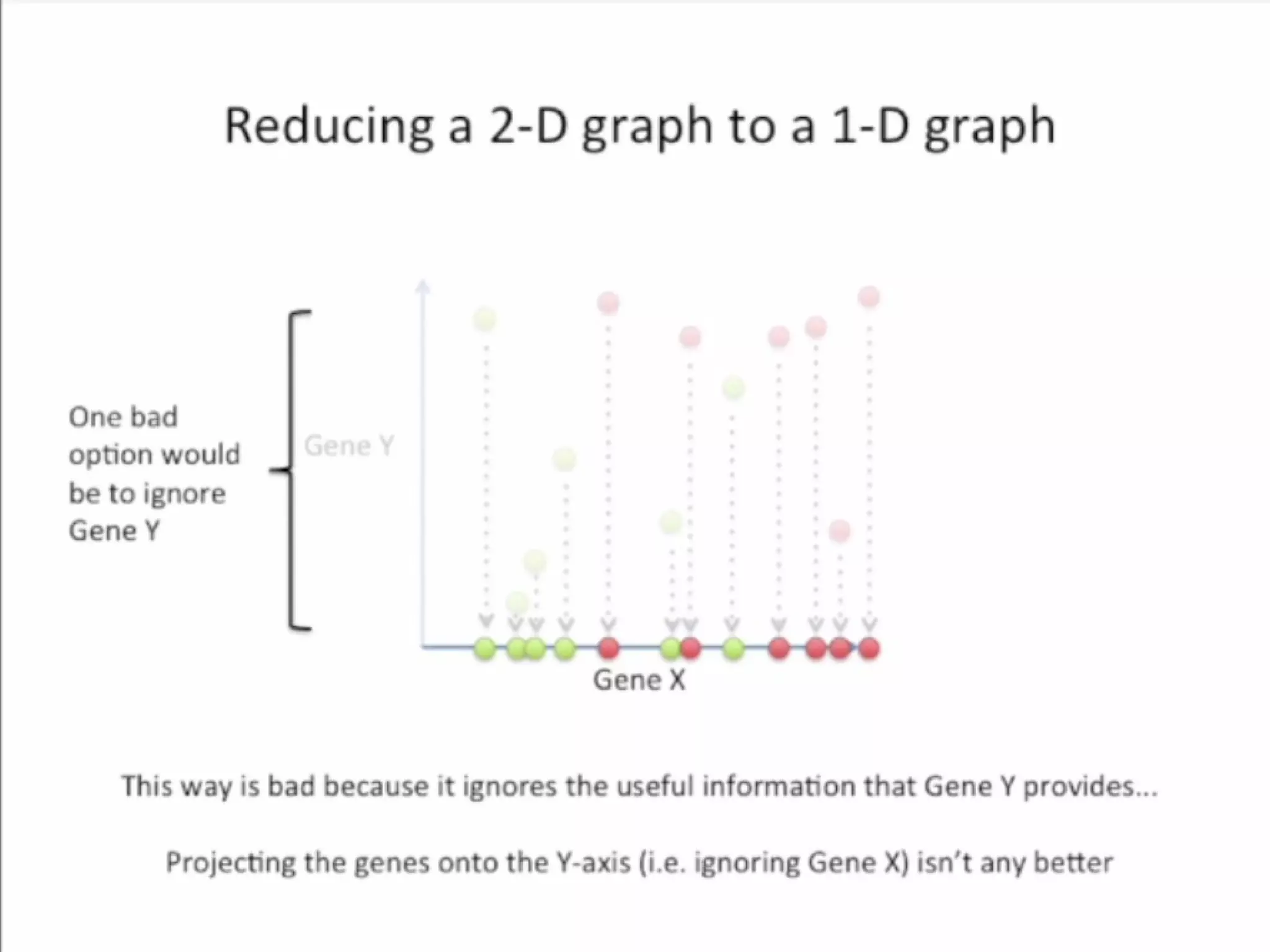
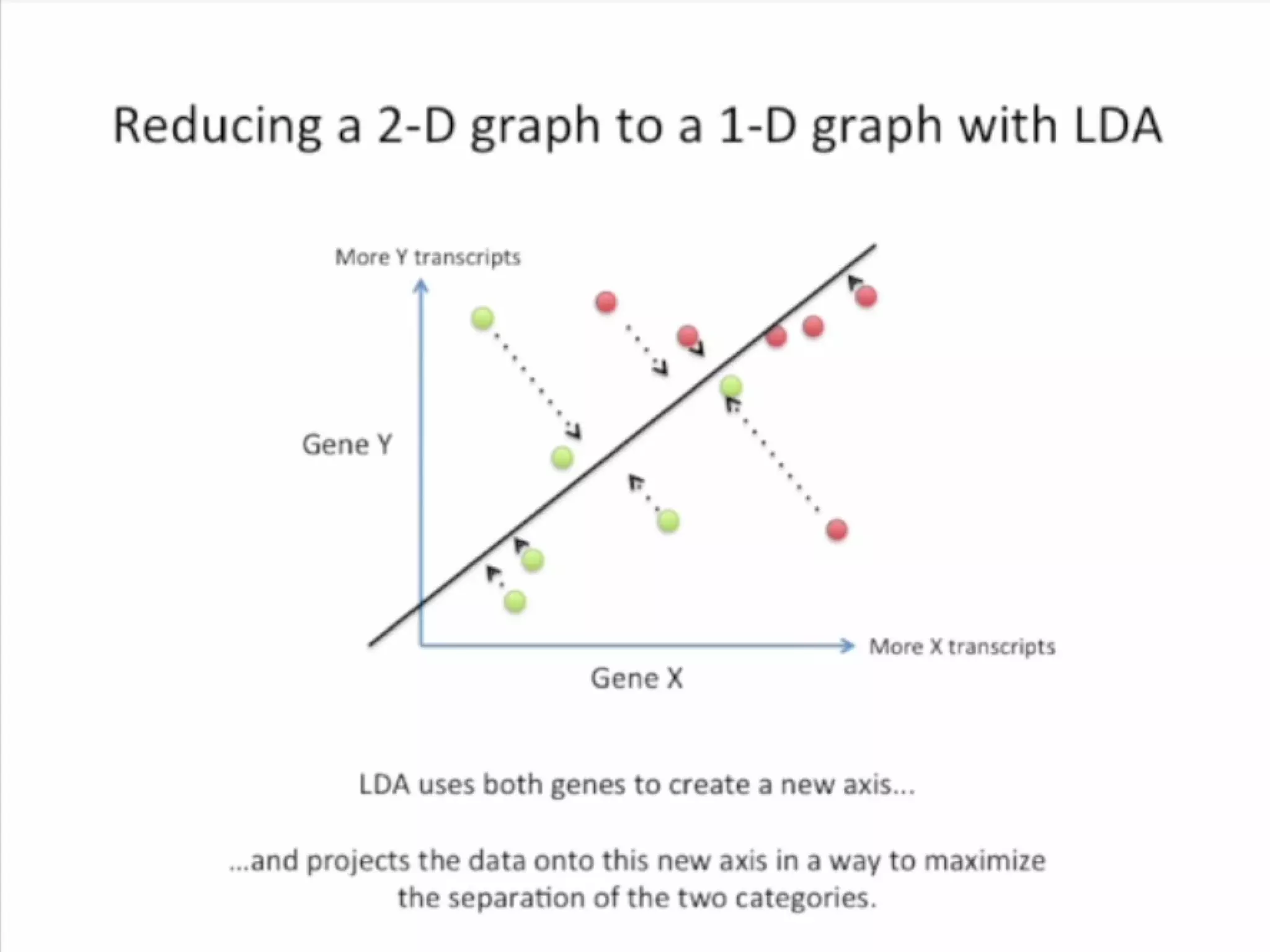
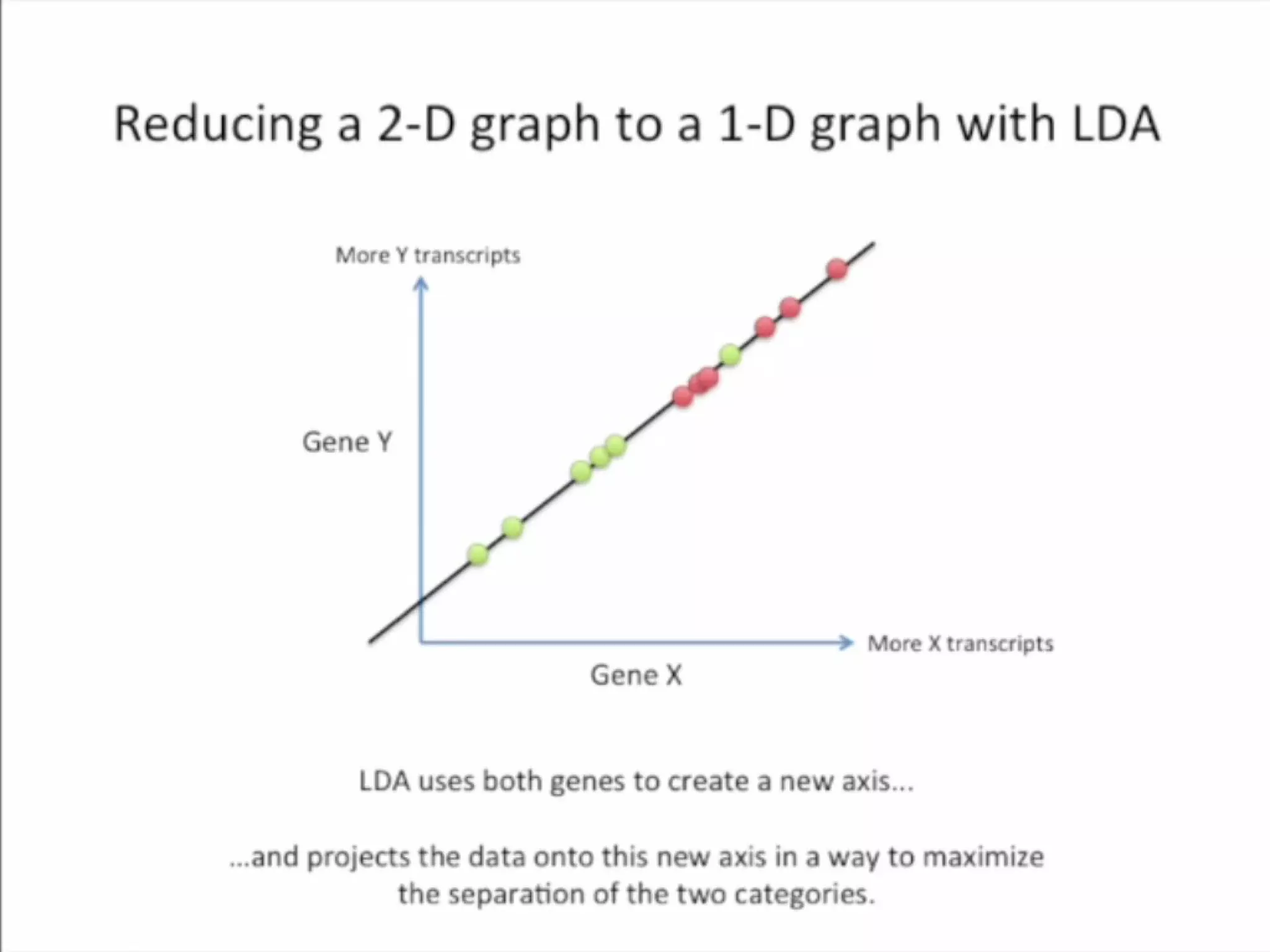
Discriminant analysis is a statistical technique used to classify cases into categories based on a set of predictor variables. It determines which continuous variables discriminate between two or more naturally occurring groups. For example, a researcher could use discriminant analysis to determine which fruit characteristics best predict whether a fruit will be eaten by birds, primates, or squirrels, based on data collected on various fruit properties from each animal group. Discriminant analysis involves estimating parameters, computing discriminant functions to classify new observations, and using cross-validation to estimate misclassification probabilities.