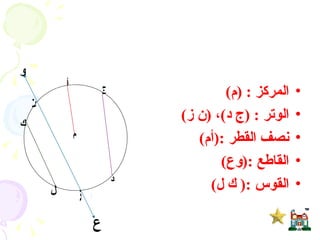
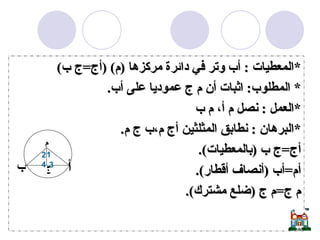
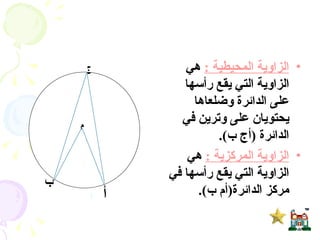
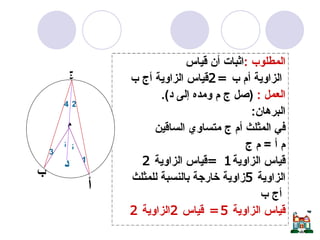
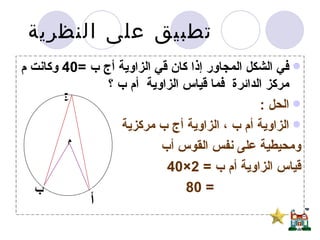
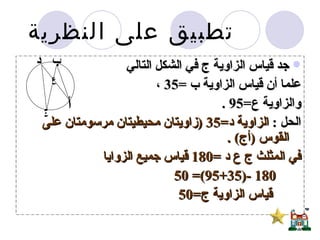
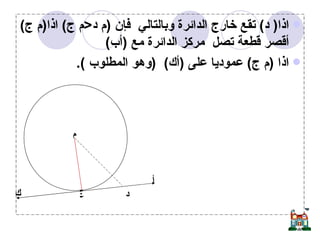
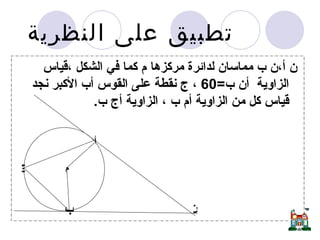
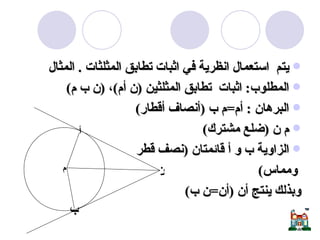
يتناول المستند دراسة الدائرة وأجزائها مثل المركز، نصف القطر، الأوتار، والمماسات، بالإضافة إلى نظريات تتعلق بالزوايا المركزية والمحيطية. يحتوي على برهانات رياضية لإثبات علاقات هندسية تتعلق بالدائرة، مثل العلاقة بين الزوايا المرسومة على نفس القوس ومفاهيم المماس ونصف القطر. يُعتبر المستند مرجعاً لدراسة الأسس الهندسية المتعلقة بالدائرة وكيفية تطبيقها في حل المشكلات الرياضية.

1. الدائرة وأجزائها أوتار الدائرة مماسات الدائرة الزاوية المركزية والزاوية المحيطية الدائرة والمماسات

2. النظرية الأولى النظرية الثانية

3. النظرية الأولى النظرية الثانية تعريف بالزوايا

4. النظرية الأولى النظرية الثانية

5. النظرية الأولى

6. الدائرة : مجموعة كل النقاط في المستوى ، التي تبعد بعدا ثابتا عن نقطة معلومة . أجزاء الدائرة : مركز الدائرة : نقطة معلومة تتوسط الدائرة . نصف القطر : القطعة المستقيمة الواصلة من مركز الدائرة الى أي نقطة من نقاطها . الوتر : القطعة المستقيمة الواصلة بين أي نقطتين من الدائرة . القاطع : مستقيم يحتوي على وتر في الدائرة . القوس : جزء من الدائرة محصور بين نقطتين منها . الدائرة وأجزائها

7. المركز : ( م ) الوتر : ( ج د ) ، ( ن ز ) نصف القطر :( أم ) القاطع :( وع ) القوس :( ك ل ) رسم توضيحي لأجزاء الدائرة م أ ج د و ع ز ن ك ل

8. أوتار الدائرة العمود النازل من مركز دائرة على أي وتر فيها ينصفه

9. المعطيات : ( أب ) وتر في دائرة مركزها ( م ) ، ( م د ) عمود على الوتر ( أب ). المطلوب : اثبات أن ( م د ) ينصف ( أب ) أي أن ( أد = دب ). البرهان : ارسم ( م أ ) ، ( م ب ) فيتكون المثلثان ( م أد ) ، ( م دب ) فيهما : م أ = م ب ( كل منهما يساوي طول نصف قطر الدائرة ). م د = م د ( ضلع مشترك ). قياس الزاوية ( أدم )= قياس الزاوية ( ب دم ) ( قائمتان بالفرض ) إذا ينطبق المثلثان بضلع ووتر وقائمة ، وينتج أن أد = دب . وهو المطلوب . م ب أ د

10. في الدائرة التي مركزها ( م ) ( م ج ) يعامد ( أب ) ،إذا كان م ج =5 سم ،م ب =13 سم، ج ب =12 سم جد طول ( أب ). الحل : م ج عمودا على الوتر ( أب ) وينصفه إلى جزأين متساويين فإذا كان طول ج ب =12 سم فإن طول أج =12 سم أي طول أب =2 ×12 = 24 سم . تطبيق على النظرية م أ ب ج

11. ... أوتار الدائرة المستقيم الواصل بين مركز دائرة ومنتصف وتر فيها غير مار بالمركز، يكون عمودا على الوتر

12. * المعطيات : أب وتر في دائرة مركزها ( م ) ( أج = ج ب ) * المطلوب : اثبات أن م ج عموديا على أب . * العمل : نصل م أ، م ب * البرهان : نطابق المثلثين أج م،ب ج م . أج = ج ب ( بالمعطيات ). أم = أب ( أنصاف أقطار ). م ج = م ج ( ضلع مشترك ). اثبات النظرية م أ ج ب 1 4 3 2

13. وينتج أن 1- الزاوية أ = الزاوية ب 2- الزاوية 1= الزاوية 2 3- الزاوية 3= الزاوية 4 لكن الزاوية 3+ الزاوية 4=180 ( لأنهما متجاورتان وعلى استقامة واحدة ) . 180/2=90 أي أن مج عمودا على أب .( وهو المطلوب ).

14. الزاوية المحيطية : هي الزاوية التي يقع رأسها على الدائرة وضلعاها يحتويان على وترين في الدائرة ( أج ب ). الزاوية المركزية : هي الزاوية التي يقع رأسها في مركز الدائرة ( أم ب ). الزاوية المحيطية والزاوية المركزية م ج أ ب

15. الزاوية المحيطية والزاوية المركزية نظرية : قياس الزاوية المركزية يساوي ضعف قياس الزاوية المحيطية المرسومة معها على القوس نفسه .

16. المطلوب : اثبات أن قياس الزاوية أم ب =2 قياس الزاوية أج ب العمل : ( صل ج م ومده إلى د ). البرهان : في المثلث أم ج متساوي الساقين م أ = م ج قياس الزاوية 1 = قياس الزاوية 2 الزاوية 5 زاوية خارجة بالنسبة للمثلث أج ب قياس الزاوية 5= قياس 2 الزاوية 2 اثبات النظرية م ج أ ب د 1 2 3 4 5 6

17. بالمثل يمكن اثبات أن قياس الزاوية 2 =6 قياس الزاوية 4 لكن قياس الزاوية أم ب = قياس الزاوية 5+ قياس الزاوية 6 اذن قياس الزاوية أم ب = 2 قياس الزاوية 2 + 2 قياس الزاوية 4 . 2 ( قياس الزاوية 2+ قياس الزاوية 4) . 2 قياس الزاوية أج ب ( وهو المطلوب ).

18. تطبيق على النظرية في الشكل المجاور إذا كان قي الزاوية أج ب =40 وكانت م مركز الدائرة فما قياس الزاوية أم ب ؟ الحل : الزاوية أم ب ، الزاوية أج ب مركزية ومحيطية على نفس القوس أب قياس الزاوية أم ب = 2×40 = 80 م ج أ ب

19. الزاوية المحيطية والزاوية المركزية الزاويتان المحيطيتان المرسومتان على قوس واحد في الدائرة لهما القياس نفسه

20. جد قياس الزاوية ج في الشكل التالي علما أن قياس الزاوية ب =35 ، والزاوية ع =95 . الحل : الزاوية د =35 ( زاويتان محيطيتان مرسومتان على القوس ( أج ) . في المثلث ج ع د =180 قياس جميع الزوايا 180 -(95+35)= 50 قياس الزاوية ج =50 تطبيق على النظرية ع أ ب د ج

21. مماسات الدائرة نظرية (1) : مماس الدائرة في نقطة ما عليها يكون عموديا على نصف القطر المار بنقطة التماس وعكس النظرية صحيح .

22. المعطيات : ( أك ) مماس الدائرة التي مركزها ( م ) عند ( ج ) ، ( م ج ) نصف القطر في الدائرة . المطلوب : اثبات أن ( م ج ) عموديا على ( أ ك ). البرهان : خذ أية نقطة ( د ) غير ( ج ) على ( أ ك ) وارسم ( م د ). بما أن ( أ ك ) مماس للدائرة عند ( ج ) فان جميع نقط ( أك ) غير النقطة ج تقع خارج الدائرة .

23. اذا ( د ) تقع خارج الدائرة وبالتالي فإن ( م د < م ج ) اذا ( م ج ) أقصر قطعة تصل مركز الدائرة مع ( أب ) اذا ( م ج ) عموديا على ( أك ) ( وهو المطلوب ). م أ ك د ج

24. ن أ،ن ب مماسان لدائرة مركزها م كما في الشكل ،قياس الزاوية أن ب =60 ، ج نقطة على القوس أب الأكبر نجد قياس كل من الزاوية أم ب ، الزاوية أج ب . تطبيق على النظرية أ م ب ن ج

25. حل السؤال الحل : الزاوية أ =90 ، الزاوية ب =90 ( مماس ونصف قطر ) الزاوية ن =60 الشكل أم ب ن شكل رباعي مجموع الزوايا =360 الزاوية م = 360-(60+90+90 ) =120 الزاوية م زاوية مركزية والزاوية ج محيطية على نفس القوس أب الزاوية ج = نصف الزاوية م =60

26. مماسات الدائرة إذا رسم مماسان لدائرة من نقطة خارجها فإن : القطعتين المستقيمتين اللتين تصلان نقطتي التماس مع نقطة تلاقي المماسين متطابقتان . 2) المستقيم الواصل بين مركز الدائرة ونقطة تلاقي المماسين ينصف الزاوية المحصورة بين المماسين وينصف الزاوية المحصورة بين نصفي القطرين المارين بنقطتي التماس .

27. يتم استعمال انظرية في اثبات تطابق المثلثات . المثال المطلوب : اثبات تطابق المثلثين ( ن أم ) ، ( ن ب م ) البرهان : أم = م ب ( أنصاف أقطار ) م ن ( ضلع مشترك ) الزاوية ب و أ قائمتان ( نصف قطر ومماس ) وبذلك ينتج أن ( أن = ن ب ) ن ب أ م

28. أب،أج مماسان لدائرة مركزها ( م ) ، أم =5 سم،م ب =3 سم جد أب،أج الحل : م ب يعامد أب أي أن المثلث ( م ب أ ) قائم الزاوية و باستخدام نظرية فيثاغورس ينتج أن ( أب × أب )=25+9 اذا ( أب × أب )=34 وكذلك أج تطبيق على النظرية م ب ج أ

29. الزاوية المماسية نظرية (2) : قياس الزاوية المماسية المحصورة بين مماس الدائرة وأي وتر مار بنقطة التماس في احدى جهتي الوتر يساوي قياس الزاوية المحيطية المرسومة على هذا الوتر من الجهة الأخرى .

30. المعطيات : ( س ص ) مماس لدائرة مركزها ( م ) في نقطة ( أ ) ، ( أب ) وتر في الدائرة، الزاوية أج ب زاوية محيطية مرسومة على الوتر ( أب ). المطلوب : اثبات أن قياس الزاوية س أب = قياس الزاوية أج ب . البرهان : صل ( أم ) ومده إلى ( د ) صل ( ب د ). أم يعامد س ص ( المماس يعامد نصف القطر عند نقطة التماس ).