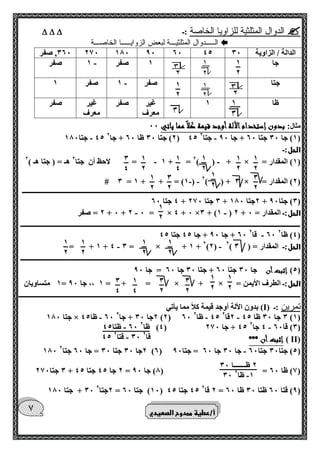
تناقش الوثيقة مفاهيم القياس في حساب المثلثات، بما في ذلك تعريف الزاوية الموجهة وطرق قياس الزوايا مثل القياس الستيني والدائري. توضح الوثيقة أيضًا العلاقة بين القياسات المختلفة وكيفية إيجاد الزوايا المكافئة وقياسات الزوايا المركزية. بالإضافة إلى ذلك، تتضمن أمثلة متنوعة لحساب الأطوال والزوايا في الدوائر.
![الربع الأول
الربع الثاني
الربع الرابع
الربع الثالث
1
ثانيا حساب المثلثات :ـ ) الفصل الثالث قياس الزاوية ( 00
تعريف الزاوية الموجهة : هي إتحاد زوج مرتب من شعاعين لهما نقطة بداية واحدة
حيث يسمى الشعاعين ضلعي الزاوية ، نقطة البداية رأس الزاوية 0
مثل > أ و ب ضلعاها ) و أ ، و ب ( ، و أ ضلع إبتدائي ، و ب ضلع نهائي
* القياس الموجب للزاوية الموجهة :
إذا كان الإتجاه من الضلع الإبتدائي إلي الضلع النهائي عكس عقارب الساعة 0
* القياس السالب للزاوية الموجهة :
إذا كان الإتجاه من الضلع الإبتدائي إلي الضلع النهائي مع عقارب الساعة 0
* الوضع القياسي للزاوية الموجهة : إذا كان ضلعها الإبتدائي هو محور السينات و رأسها نقطة الأصل
ملاحظات هامة :ـ ] 1[ الزاوية الموجهة أ و ب الزاوية الموجهة ب و أ
2[ لكل زاوية موجهة في وضعها القياسي قياسان أحدهما موجب و الأخر سالب بحيث يكون [
مجموعهما العددي 060
- - - 000000000 ) 60 ، 000 ( // ) 210 ، 150 ( / ) 240 ، مثال: ) 120
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
طرق قياس الزاوية :ـ ) القياس الستيني و القياس الدائري ( 000
//60 = /1 ، / 60 = أولاً القياس الستيني:ـ وحدة قياسه هي الدرجات والدقائق والثواني بحيث 1
ملاحظات هامة جداً 00
1( ينقسم المستوي إلي أربعة أرباع كما هو موضح (
2( الزوايا المتكافئة : هي الزوايا التي لها ضلع (
نهائي واحد 0
و تكون الزاويا التي تكافئ
063 × > هـ = هـ + ن
أي نجمع أو نطرح 060 للحصول علي زوايا متكافئة
] 060 ، 0( لمعرفة الربع الذي تقع فيه الزاوية لابد و أن تكون موجبة و محصورة في ] 0 (
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
مثال: حدد الربع الذي تقع فيه الزوايا الأتية ثم أوجد زاوية مكافئة لكل منها ؟
- - 5( ط / 5 ( 400 )4( 040 )0( 140 )2( 440 )1(
- 00 تقع في الربع الأول ،، 440 تكافئ 00 = ) 060 ( 440 = 440 ) الحل:ـ ) 1
- - 220 : تقع في الربع الثالث ، و تكافئ 220 = 060 + 140 = 140 )2(
- 120 : تقع في الربع الثاني و تكافي 120 = ) 060 ×2 ( 040 = 040 )0(
- - 020 : تقع في الربع الرابع و تكافئ 020 = ) 060×2 ( + 400 = 440 )4(
00000 096 = 060 + 06 تقع في الربع الأول و تكافئ 06 = 5 / 100 = 5( ط / 5 (
أ/عطية ممدوح الصعيدي](https://image.slidesharecdn.com/11-140907130939-phpapp01/75/1-1-1-2048.jpg)
![ل
نق
ل
هـء
ل
نق
ل
نق
هــء
ط
س
100
س × ط
100
هــء ×100
ط
ط × س
100
ط × 225
100
120
100
60
100
144
100
1و 1
طء
5 طء/ 16
طء
ل
نق
2
ثانياً القياس الدائري :ـ القياس الدائري لزواية مركزية تحصر قوس طوله ل في دائرة
طول نصف قطرها نق هو هـء = نق ،، نق = ] × ل = هـء ]
تعريف الزاوية النصف قطرية :ـ هي زاوية مركزية تحصر قوس طول = طول نصف قطر الدائرة 0
مثال 1: زاوية مركزية في دائرة طول نصف قطرها 15 ســـــــم تحصر قوس طوله 25 ســــــــم
ـ أوجد قياسها بالتقدير الدائري ؟
الحل:ـ ჻ ل= 25 ، نق = 15 سم 66 و 1 ء = 15 / هـ ء = = 25
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
2( زاوية مركزية قياسها 2و 1ء تحصر قوس طوله 12 سم أوجد طول نصف قطر هذه الدائرة ؟ (
الحل:ـ ჻ هـء = 2و 1ء ، ل= 12 سم 10 سم = 2و 1 / نق = ل / هـء = 12
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
0( زاوية مركزية قياسها 2و 2 ء في دائرة طول نصف قطرها 15 سم أوجد طول القوس الذي تحصره؟ (
الحل:ـ ჻ هـء = 2و 2 ، نق = 15 سم 00 سم 00 = 15 × نق = 2و 2 × ل = هـء
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
4( زاوية مركزية تحصر قوس طوله 20 سم في دائرة محيطها 44 سم أوجد قياسها الدائري ؟ (
الحل:ـ ჻ ل = 20 سم ، محيط الدائرة = 2 ط نق نق × )7 /22 ( × 2 = 44 نق = 7 سم
06 و 2ء # = 7 / هـء = = 20
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
العلاقة بين التقديرين الدائري و الستيني:ـ =
هـء = ،،، س = ***
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
- ] 4 ط / 5 ،، 420 ،، 240 ،، مثال 5: أوجد القياس الدائري للزاويا الأتية ] 225
الحل:ـ ჻ س = 225 7 / هـء = = = 9و 0 ء لاحظ أن ط = 22
** ჻ - - 120 = 060 + 240 = س = 240 ط = 1و 2ء × = هـء
- 60 = 060 ** س = 420 ط = 047 و 1 ء × = هـء
144 = 5÷ 100×4 = ** س = 4 ط / 5 ط = 5و 2 ء # × = هـء
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
6( أوجد القياس الستيني لكل من 1و 1 ء ،، 5 طء / 16 (
الحل:ـ ჻ هـء = 1و 1 60 = 100 × = س
، ** ჻ هـء = 5 ط ء/ 16 25 و 56 = 100 × = س
7( زاوية مركزية تحصر قوس طوله 20 سم في دائرة طول قطرها 24 سم 0 (
ـ أوجد قياسها الدائري و الستيني ؟
أ/عطية ممدوح الصعيدي](https://image.slidesharecdn.com/11-140907130939-phpapp01/85/1-1-2-320.jpg)


![ص
س
جا هـ
جتا هـ
1
ص
1
جا هـ
1
س
1
جتاهـ
س
ص
جتاهـ
جا هـ
الكل موجب
جا + ، قتا +
جتا+ ، قا +
ظا + ، ظتا+
0
5
0
5
9
25
9
25
16
25
4
5
0
5
4
5
0
5
0
5
4
5
5
تعريف : إذا كان الضلع النهائي لزاوية موجهة في الوضع القياسي
يقطع دائرة الوحدة في النقطة ) س ، ص ( فإن
1( جا هـ = ص ، ) 2( جتا هـ = س ، ) 0( ظا هـ = = (
و تسمي هذه الدوال الثلاثة بالدوال المثلثية الأساسية 00
مقلوبات الدوال المثلثية :ـ
1( قتا هـ = = ) 2( قا هـ = = ) 0( ظتا هـ = = (
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
مثال 1: إذا كان الضلع النهائي لزاوية ) هـ ( في وضعها القياسي يقطع دائرة الوحدة في النقطة
6و ، 0و( ـ أوجد الدوال المثلثية لهذه الزاوية ؟ (
4 / الحل:ـ جا هـ = ص = 0و ،، جتا هـ = س = 0و ، ظا هـ = ص / س = 6و / 0و = 0
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
] ملاحظات هامة :ـ ] 1
] إشارات الدوال المثلثية [ كما هو مبين في الشكل
و يجب قبل تحديد إشارة الدالة المثلثية تحديد الربع
مثال 2 : حدد إشارات الدوال الأتية
جا 60 ، جتا 240 ، ظا 210 ، قا 000
- جتا 150 ، ظا 00
الحل:ـ
჻ 60 تقع في الربع الأول ) + ( جا 60
჻ 240 تقع في الربع الثالث - ) ( جتا 240
჻ 210 تقع في الربع الثالث 000 في الربع الرابع ،، ) + ( ظا 210 )+( قا 000
჻ 150 تقع في الربع الثاني 000 في الرابع - - = 00 ،،، ) ( جتا 150 - - ) ( ظا 00
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
2[ إذا كان الضلع النهائي للزاوية الموجهة في وضعها القياسي يقطع دائرة الوحدة في النقطة [
1 ** ] من نظرية فيثاغورس [ = )س، ص( فإن س 2 + ص 2
مثال 3: إذا كان الضلع النهائي لزاوية هـ في وضعها القياسي يقطع دائرة الوحدة في النقطة ) س، (
فأوجد قيمة س حيث س ح + ثم أوجد جا هـ ، ظا هـ ، قا هـ
الحل:ـ 1 = س 2 + ص 2 1 = 2) ( + س 2 1 = + س 2
- = 1 = س 2 س = النقطة هي ) ، (
# 4/ 4/0 ،، قا هـ = 5 = ÷ = جا هـ = ،، ظا هـ](https://image.slidesharecdn.com/11-140907130939-phpapp01/85/1-1-5-320.jpg)

![ط × س
100
ط ×20
100
1
2
1
2
1
2
1
2
1
4
0
2
0
4
جا 17
جتا 70
45 جتا 2 س+ جتا 2
45 ظا 2
0
بعض خواص الدوال المثلثية :ـ ] 1[ الدوال المثلثية للزاويتين المتتامتين هـ ، 06 هـ [ -
1( جا هـ = جتا ) 90 هـ( ) 2( جتا هـ = جا) 90 هـ ( ) 0( ظا هـ = ظتا) 90 هـ ( - - - (
بالمثل : قتاهـ = قا) 90 هـ ( ،، قا هـ = قتا ) 90 هـ( - -
ملاحظة : إذا كان جا س = جتا ص فإن س+ ص = 90 و بالمثل باقي الدوال 0000
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
00000 ، مثال 1:ـ جا 02 = جتا 50 ، ظتا 20 = ظا 70 ،، قا 65 = قتا 25
2( إذا كانت جتا ) س+ 25 ( = جا ) 2س 10 ( فأوجد قيمة س حيث س - ( [ 0 ، ط/ 2 ]
الحل:ـ - ) جتا) س+ 25 ( = جا ) 2س 10 - 90 = 2س 10 + س+ 25
90 = 0س+ 15 0س = 75 س = 25
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
0( إذا كانت ظا ) 0س+ 20 ( = ظا ) س 10 ( فأوجد قيمة س بالتقدير الدائري ؟ - (
الحل:ـ ჻ - ) ظا ) 0س+ 20 ( = ظا ) س 10 - 90 = 0س+ 20 + س 10
90 = 4س+ 10 4س = 00 س = 20
سء = = = 05 وء
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
4( إذا كانت قا 2هـ = قتا ) 0هـ 60 ( فأوجد قيمة هـ ثم أوجد قيمة المقدارجا هـ + 2جتا 2هـ + جا 0هـ - (
الحل:ـ ჻ - ) قا 2هـ = قتا ) 0هـ 60 - 90 = 2هـ + 0هـ 60 5هـ = 150 هـ = 00
჻ @ 2 = 1 + ×2 + = 2جتا 60 + جا 90 + المقدار = جا 00
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
2س= 1 2س+ جتا 2 5( إذا كانت ظا ) 2س+ 9( = ظتا ) س+ 06 ( فأوجد قيمة س ثم إثبت أن جا 2 (
الحل:ـ ჻ ) ظا ) 2س+ 9( = ظتا ) س+ 06 90 = 2س+ 9+ س+ 06 90= 0س+ 45
0س= 45 # س = 15
1= + = 2) ( + 2) ( = 00 00 + جتا 2 15 = جا 2 ×2 15 + جتا 2 ×2 المقدار = جا 2
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
تمرين:ـ ) 0( أكمل ما يأتي
)أ( ظتا 54 = ظا 00000 )ب( قا 75 = قتا 0000 )جـ( جتا 50 = جا 0000 )د( = 0000
2( أوجد قيمة س إذا كان جا س = جتا 2س ثم أوجد قيمة المقدار جا س جتا 2س جا 0س (
- ) 0( أوجد قيمة هـ إذا كان ظا ) 2س+ 25 ( = ظتا ) 0س 5 (
4( أوجد قيمة ص بالتقدير الدائري إذا كانت قتا ) 0ص( = قا) 50 ص( - (
- ) 5( إذا كانت جتا ) س+ 50 ( = جا ) 2س 50 (
ـ فأوجد قيمة س ـ ثم أوجد قيمة المقدار = جتا 2 س + جا 0س + جتا 270 ظا 45
) 6( إذا كانت جتا )س+ 20 ( = جا ) س= 10 (
ـ فأوجد قيمة س ـ ثم أوجد قيمة المقدار
)7( أ ب جـ فيه أ ب = ب جـ ، جا أ = جتا جـ أوجد قياسات زواياه ؟](https://image.slidesharecdn.com/11-140907130939-phpapp01/85/1-1-8-320.jpg)
![1
2
0
2
1
2
0
2
1
2
0
2
0
2
1
2
1
2
1
2
1
2
1
2
1
2
9
- 11 هـ [ 00 تابع الخواص : ] 2[ الدوال المثلثية للزاويتين المتكاملتين ] هـ ، 6
1( جا ) 100 هـ = جا ) هـ ( ) 2( جتا ) 100 هـ ( = جتا هـ ) 0( ظا ) 100 هـ ( = ظا هـ - - - - - (
] [ْ الدوال المثلثية للزاويتين هـ ، 116 + هـ 000
1( جا ) 100 + هـ ( = جا هـ ) 2( جتا ) 100 + هـ ( = جتا هـ ) 0( ظا ) 100 + هـ ( = ظا هـ - - (
- 4[ الدوال المثلثية للزاويتين هـ ، 06 هـ 000 [
1( جا ) 060 هـ (= جا هـ ، ) 2( جتا ) 060 هـ ( = جتا هـ ) 0( ظا ) 060 هـ ( = طا هـ - - - - - (
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ملاحظات ) 1( لأيجاد دالة أي زاوية و معرفة قيمتها لابد من تحديد الربع أولاً ثم إختيار زاوية مناسبة
60 ،، 45 ،، من الزوايا 00
- - - 60 100 = 120 // 45 100 = 105 // 00 100 = 2( زاويا الربع الثاني هي 150 (
60 +100 = 240 // 45 +100 = 225 // 00 +100 = 0( زوايا الربع الثالث هي 210 (
- - - 60 060 = 000 // 45 060 = 015 // 00 060 = 4( زوايا الربع الرابع هي 000 (
5( جا ) هـ ( = جا هـ // جتا ) هـ ( = جتا هـ // ظا ) هـ ( = ظا هـ - - - - - (
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
مثال: أوجد قيمة كلاً مما يأتي 00
1( جتا 120 ظا 015 + جا 240 ظا 000 (
الحل:ـ ჻ - - - = 60 ( = جتا 60 جتا 120 = جتا ) 100
- - - 1 = 45 ( = ظا 45 ،، ظا 015 = ظا) 060
- - = 60 ( = جا 60 + ، جا 240 = جا ) 100
- - - = 60 ( = ظا 60 ،، ظا 000 = ظا) 060
- - - - - 1 = = × 1 × = المقدار
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
2جتا ) 105 ( قتا 45 جا 90 = س فأوجد قيمة س ؟ - + 2( إذا كانت جتا 000 ظتا 240 (
- = 00 ( = جتا 00 الحل:ـ جتا 000 = جتا) 060
= 60 ( = ظتا 60 + ، ظتا 240 = ظتا) 100
- - - - = 45 ( = جتا 45 ،، جتا) 105 ( = جتا 105 = جتا) 100
1 = = صفر - - × × ×2 + × = المقدار
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
- 00 225 0( أوجد قيمة جتا 400 جا 00 ظا 2 (
- - - = 6( = جتا 60 120 ( = جتا 120 = جتا) 100 + الحل:ـ جتا 400 = جتا ) 060
- - 1 = 45 ( = ظا 45 + جا 00 = جا 00 = ،، طا 225 = ظا ) 100
4
أ/عطية ممدوح الصعيدي - - / 1 = 2)1( × × = المقدار](https://image.slidesharecdn.com/11-140907130939-phpapp01/85/1-1-9-320.jpg)

![0س
5
- 1
2
- 1
2
- 0
4
1
4
11
أوجد مجموعة حل المعادلات الأتية : س 2 ط ] ، 0 ]
2 جا س 1 = صفر ) 0( جا س جتا س = صفر - )2( 1( ظا س = 1 (
الحل:ـ
)1( ჻ ، ظا س = 1 ჻ 1 = ظا 45 س = 45 لكن ظا هـ موجبة في الربعين الأول و الثالث
225 = 100 + س= 45 }225 ، م ح = } 45
)2( ჻ 2جا س = 1 جا س = 5و س = 00 لكن جا هـ موجبة في الربعين الأول و الثاني
- 150 = 00 س = 100 } 150 ، م ح = } 00
)0( ჻ جا س جتا س = 0 إما جا س = 0 0 أ، جتا س= 0 ، س = 100 س= 90،270
} 270 ، 100 ، 9 ، م ح = } 0
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
- 0 = 2جا 2 س + جا س 1 )6( 1 = ) 2جتا س + 1 = صفر ) 5( جا ) 2س+ 10 )4(
الحل:ـ ) 1( جتا س = 5و ، - ჻ 5و ، = جتا 60 ჻ جتا هـ سالبة في الربعين الثاني و الثالث
- 240 = 60 + 120 أ، س = 100 = 60 س = 100
)5( ჻ 1 = جا 90 90 = 2س+ 10 2س = 00 س = 20
6( بالتحليل ( - 0 = ) 2جا س 1() جا س+ 1 ( - جاس = 5و أ، جا س= 1
عندما : جا س= 5و - س= 00 أ، 150 ،، عندما : جا س = 1 س = 270
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
7( حل المعادلة : جا 60 جا 000 جتا 120 جا ) 150 ( = جتا س - - (
جتا س - - = × × الحل:ـ - - جتا س = = 1
჻ - جتا س = 1 س = 100
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
تمريـــــن : ) 0( أكمل ما يأتي 00
)أ( إذا كانت 2 جا س = 1 فإن جتا س = 00000000 أ، 00000000
)ب( إذا كانت ظا س = 1 فإن جا س = 0000000000 أ، 000000000
- )جـ( إذا كانت قتاس = 2 فأن قا س = 0000000000 أ، 000000000
2( أوجد مجموعة حل المعادلات الأتية 00 (
)أ( 2 جتـــــــا س = 1 )ب( ظا 2 س 1 = صفــــــــــــــــــــر -
- )جـ( 2 جا س = صفر ) د ( ظا ) ( = 1
- - @ 1 = ) ) هـ( جتا 2 س جتا س = صفر ) و( جتا ) 0س + 00](https://image.slidesharecdn.com/11-140907130939-phpapp01/85/1-1-11-320.jpg)
![أ ب
أ جـ
مقابل
وتر
ب جـ
أ جــ
مجاور
وتر
أ ب
ب جـ
مقابل
مجاور
ب جـ
أ ب
ب جـ
أ جـ
ب جـ
أ جـ
أ ب
أ جـ
4
5
0
5
16
25
9
25
7
25
1
2
0
5
1
2
1
2
0
5
1
2
4
5
- 0
10
4
10
- - ظا ) 90 ص( جا س + جا 00
- 2 جا 60 ظا 60 45 جتا 2
- 5
12
- 0
5
0
5
1
2
12
الدوال المثلثية للزوايا الحادة :ـ في أي أ ب جـ قائم في ب
يكون جا جـ = = ،، جتا جـ = =
ـ ظا جـ = = ، بالمثل قتا جـ = وتر / مقابل ، قا جـ = وتر / مجاور، ظتا جـ = مجاور / مقابل
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
: مثال 1 أ ب جـ فيه > ب قائمة ، أ ب = 0 سم ، أ جـ = 5 سم
ـ أوجد ظا أ ، جا ) 100 أ ( ، جا ) 90 جـ ( ، قتا ) جـ ( - - -
الحل:ـ
- - 16 = 9 25 = من فيثاغورس : ) ب جـ ( 2 = )أ جـ ( 2 ) أ ب ( 2 أ جـ = 4ســــم
- 5 / 0 ** جا ) 100 أ ( = جا أ = = 4 / ظا أ = = 4
- - - - 5 / 5 ** قتا ) جـ ( = قتا جـ = = 0 / ، جا ) 90 جـ ( = جتا جـ = = 4
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
2( إذا كانت 4ظا هـ = 0 حيث هـ زاوية حادة فأوجد قيمة كلاً من (
أ ـ جتا 2 هـ جا 2 هـ ** ب ـ جتا 120 جا ) 100 هـ ( + جا 510 جتا هـ - -
الحل:ـ
- - = = 2) ( أ ـ المقدار= ) ( 2
- - - = 60 ( = جتا 60 ب ـ جتا 120 = جتا ) 100
- = ، جا ) 100 هـ ( = جا هـ = ،، جا 510 = جا 150 = جا 00
- @ 10 / 1 = + = × + × = المقدار
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
0( إذا كانت 4 ظا س = 0 حيث س ( - 0 حيث 90 > ص > 100 = 10 جا ص 12 ، [ [ ط ، 0ط/ 2
فأوجد قيمة المقدار
الحل:ـ
لاحظ أن س تقع في الربع الثالث ،، ص تقع في الربع الثاني ] تذكر الإشارات[
ظا ) 90 ص( = ظتا ص = ،، جا س = جا س = = - - - -
= 2) ( = 45 ، جتا 2
10 / المقدار = = 1
أ/عطية ممدوح الصعيدي](https://image.slidesharecdn.com/11-140907130939-phpapp01/85/1-1-12-320.jpg)
![- 15
0
15
0
- 4
5
1
2
15
0
4
5
1
2
00
20
4
5
10
4 ظا جـ = 0 حيث 100 > جـ > 270 ، 4( إذا كان 17 جا ب = 0 حيث 90 > ب > 100 (
- - - - ) جتا ) 400 × ) قتا 000 + قا ) 100 جـ × ) فأوجد قيمة المقدار : ظتا ) 100 ب
4 ، جـ في الربع الثالث / 17 حيث ب في الربع الثاني ،، ظا جـ = 0 / الحل:ـ جا ب = 0
ظتا) 100 ب ( = ظتا ب = = - - -
- - - - - - 2 = ) 00 ( = ) قتا 00 ، قتا 000 = قتا 000 = قتا ) 060
، قا ) 100 جـ ( = قا جـ = - -
- - = ، جتا) 400 ( = جتا 400 = جتا 120
- - # = × 2 × = المقدار
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
تمريــــــــن :ـ
)1( أ ب جـ قائم الزاوية في ب ، فيه أ ب = 6سم ، ب جـ = 0 سم
ـ أوجد ظا ) 100 + أ ( ،، جتا ) 90 جـ ( ،، قا ) أ ( ،، جتا ) 100 + جـ ( - -
2( إذا كانت 0 ظا هـ = 4 حيث هـ ( [ 100 ، 0 ]
- - ـ فأوجد قيمة المقدار 5 جتا هـ + ظا ) 100 هـ ( + جتا 120 ظا 015
0 حيث ب = 0( إذا كانت 25 جا ب + 24 ( [ 270 ، 100 ]
5 ظا جـ 12 = صفر حيث جـ أكبر زاوية موجبة - ،
ـ فأوجد قيمة المقدار جا ) 100 + ب ( + جتا ) 100 جـ ( -
4( إذا كانت جا س = حيث س أكبر زاوية موجبة (
ـ فأوجد قيمة المقدار قتا) 100 س ( طا س جتا ) 100 + س ( - -
- 5( بإستخدام الألة الحاسبة أوجد قيمة المقدار جتا 20 + ظا 42 جا 200 (
- 6( بإستخدام الألة أوجد قيمة المقدار حا 15 جا 15 جتا 15 جتا 15 (
7( حل المعادلة جا س = 2045 و 0 (
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
مع أطيب و أرق الأمنيات للجميع بالتفوق***
* أ/ عطية ممدوح الصعيدي *](https://image.slidesharecdn.com/11-140907130939-phpapp01/85/1-1-13-320.jpg)