Квадратное неравенство

1. Квадратна нерiвнiсть.Квадратна нерiвнiсть.
Розв’язування квадратнихРозв’язування квадратних
нерiвностейнерiвностей
Презентацію створено за допомогою комп’ютерної програми ВГ
«Основа» «Електронний конструктор уроку»

2. 9 21) x −
3
2)
x
1
;
3
x =
3 15
;
5
3)
×
1.1. Знайдiть значення виразу:
при x = 3;
при
4) (−1,32−2,18) 0,6.⋅
Виконання усних вправВиконання усних вправ

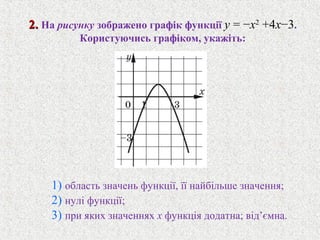
3. 2.2. На рисунку зображено графiк функції y = −x2
+4x−3.
Користуючись графiком, укажiть:
1) область значень функцiї, її найбiльше значення;
2) нулi функцiї;
3) при яких значеннях x функцiя додатна; вiд’ємна.

4. 1 3
;
2 2 2
3)
x
− < − < −
1 1
1 .
3
4)
x
> >
3.3. Вiдомо, що 1 < x < 3. Яка з наведених нерiвностей є
неправильною?
1) 3 < x+2 < 5;
2) 3 < 3x < 9;

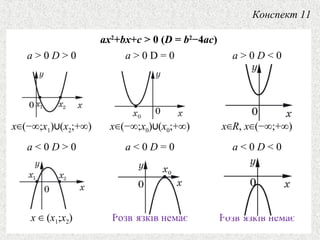
5. Означення. Нерiвнiсть вигляду ax2
+bx+c > 0 (< 0, > 0, ≤ 0)
називається квадратною, якщо a ≠ 0.
Щоб розв’язати квадратну нерiвнiсть, достатньо знайти коренi
квадратного тричлена й побудувати ескiз його графiка
(параболу). Як вiдповiдь записуються промiжки осi Ox, для яких
точки параболи розмiщенi вище вiд осi Ox (для випадку > 0) i
нижче вiд осi Ox (для випадку < 0).
(Якщо квадратний тричлен має два рiзних коренi x1 i x2, можна
також використати метод iнтервалiв — див. табл. 40.)
Конспект 11
Квадратнi нерiвностiКвадратнi нерiвностi

6. ax2
+bx+c > 0 (D = b2
−4ac)
a > 0 D > 0
x (−∞;∈ x1) (∪ x2;+∞)
a > 0 D = 0
x (−∞;∈ x0) (∪ x0;+∞)
a > 0 D < 0
x∈R, x (−∞;+∞)∈
a < 0 D > 0
x (∈ x1;x2)
a < 0 D = 0
Розв’язкiв немає
a < 0 D < 0
Розв’язкiв немає
Конспект 11

7. 1.1. На рисунку зображено графiк функцiї y = x2
−x−2.
Назвiть множини розв’язкiв нерiвностей:
1) x2
−x−2 > 0;
2) x2
−x−2 < 0;
3) x2
−x−2 ≥ 0;
4) x2
−x−2 ≤ 0.
Виконання усних вправВиконання усних вправ

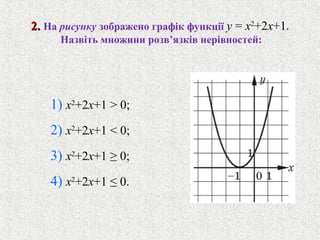
8. 2.2. На рисунку зображено графiк функцiї y = x2
+2x+1.
Назвiть множини розв’язкiв нерiвностей:
1) x2
+2x+1 > 0;
2) x2
+2x+1 < 0;
3) x2
+2x+1 ≥ 0;
4) x2
+2x+1 ≤ 0.

9. 1.1. Розв’яжiть нерiвнiсть:
1) x2
+6x+8 > 0; 2) x2
+5x−14 ≤ 0; 3) −x2
+6x+7 ≥ 0.
1) x2
+3x−4 < 0; 2) x2
+3x−4 > 0; 3) 2x2
−3x < 0;
4) −x2
−2x+3 > 0; 5) −2x2
+5x−3 < 0; 6) 2x2
−8 > 0.
Виконання письмових вправВиконання письмових вправ
2.2. Розв’яжiть нерiвностi:

10. ( ) ( )
2
2 5 5 ;3) x x x− ≤ +
2
2 3 4
1;
5 8
4)
x x+ −
− ≤ −
4.4. Знайдiть множину розв’язкiв нерiвностi:
5) (3x−8)2
−(4x−6)2
+(5x−2)(5x+2) > 96.
3.3. Розв’яжiть нерiвнiсть:
1) x2
≤ 9; 2) x2
> 7; 3) 7x2
≤ 3x;
4) −5x2
> 10x; 5) −3x2
< −75; 6) 0,6x2
< −18x.
1) (3x+1)(x−2) < 6; 2) (x+3)2
−16 > (1−2x)2
;

11. Знайдiть найбiльше й найменше значення функцiї та
промiжки її зростання; спадання:
( ) 21
2 3;
7
2) f x x x= − + +
3) f(x) = 20−12x−0,4x2
; 4) f(x) = 3x2
+7x.
Виконати вправу на повторення.Виконати вправу на повторення.
1) f(x) = x2
+4x−16;

12. Якi з наведених нерiвностей виконуються для будь-яких
дiйсних значень x?
Тестове завданняТестове завдання
А) −2x2
+x+6 < 0; Б) 2x2
+x+7 > 0;
В) x2
> 0; Г) −3x2
−x−6 < 0.

13. 1) x2
> 4; 2) x2
< 1; 3) −2x2
> −2; 4) x2
≤ 5x.
Домашнє завданняДомашнє завдання
Вивчити означення квадратної нерiвностi, схему її
розв’язання (див. конспект 17).
Виконати вправи.
1.1. Розв’яжiть нерiвнiсть:
1) x2
+x−6 < 0; 2) x2
+5x−14 ≥ 0; 3) −x2
+6x+7 ≤ 0.
2.2. Розв’яжiть нерiвнiсть:

14. 2
1 3 2
;
4 6 3
3)
x x− +
− ≤ −
2
3 2 3 8 9 1
.
6 9 36 4
4)
x x x x− + − +
+ < −
3.3. Розв’яжiть нерiвнiсть:
Повторити знаходження областi визначення функцiї, заданої
рiвнянням виду y = f(x); означення системи нерiвностей, а
також змiст поняття дискримiнанта квадратного рiвняння.
1) x(2x+3) ≤ (2x+3)(2x−1);
2) (3x−1)2
−(x−1)2
> 4(x+4);

15. Виконати вправу на повторення.
Побудуйте графiк функцiї f(x) = x2
−2x−3. Користую чись
графiком, знайдiть:
1) f(2), f(−1,5), f(2,5);
2) значення x, при яких f(x) = 5, f(x) = −4, f(x) = −1;
3) нулi функцiї;
4) найбiльше й найменше значення функцiї;
5) область значень функцiї;
6) розв’язки нерiвностi f(x) < 0, f(x) > 0.

16. Презентацію створено за допомогою комп’ютерної програми ВГ
«Основа» «Електронний конструктор уроку»
© ТОВ «Видавнича група ˝Основа˝», 2012
Джерела:
1. Усі уроки алгебри. 9 клас./ С. П. Бабенко — Х.: Вид. група
«Основа», 2009.— 304 с. — (Серія «12-рiчна школа»).