Download to read offline
Урок 02 Розвʼязування типових вправ за темою «Числова функція. Графік функції».pptx
- 1. Розвʼязування типових вправза темою «Числова функція. Графік функції» 24.09.2023 24.09.2023 10 клас Урок 02 Алгебра і початки аналізу
- 2. ПРИГАДАЄМО // Найпростішіперетворення графіків функцій 𝑥 𝑦 𝑂 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 -1 -2 -3 -2 -3 -4 -5 𝑥 𝑦 𝑂 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 -6 -7 -8 -2 -3 -4 -5 𝑦 = 𝑓 𝑥 + 𝑛 𝑦 = 𝑓 𝑥 − 𝑛 +𝑛 ↑ −𝑛 ↓ 𝑛 > 0 𝑦 = 𝑥 𝑦 = 𝑥 + 3 𝑦 = 𝑥 − 4 𝑦 = 𝑓 𝑥 + 𝑚 −𝑚 ← 𝑦 = 𝑥2 𝑦 = 𝑥 + 4 2 𝑦 = 𝑓 𝑥 − 𝑚 +𝑚 → 𝑦 = 𝑥 − 5 2 𝑚 > 0 Поясніть, як побудувати графік функції 𝑦 = 𝑥 + 3 Поясніть, як побудувати графік функції 𝑦 = 𝑥 − 4 Поясніть, як побудувати графік функції 𝑦 = 𝑥 + 4 2 Поясніть, як побудувати графік функції 𝑦 = 𝑥 − 5 2 Перенесення кожної точки графіка праворуч або ліворуч на 𝑚 одиниць Перенесення кожної точки графіка вгору або вниз на 𝑛 одиниць
- 3. ПРИГАДАЄМО // Найпростішіперетворення графіків функцій 𝑥 𝑦 𝑂 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 -1 -2 -3 -2 -3 -4 -5 𝑦 = −𝑓 𝑥 𝑦 = 𝑥 𝑦 = − 𝑥 𝑦 = 𝑘𝑓 𝑥 Стиск 𝑦 = 𝑘𝑓 𝑥 Розтяг 0 < 𝑘 < 1 𝑘 > 1 𝑥 𝑦 𝑂 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 -1 -2 -3 -4 -5 -6 -7 -8 -2 𝑦 = 𝑥2 𝑦 = 1 2 𝑥2 𝑦 = 2𝑥2 Поясніть, як побудувати графік функції 𝑦 = − 𝑥 Поясніть, як побудувати графік функції 𝑦 = 1 2 𝑥2 Поясніть, як побудувати графік функції 𝑦 = 2𝑥2 Графіки функцій 𝑦 = −𝑓 𝑥 і 𝑦 = 𝑓 𝑥 симетричні відносно осі 𝑂𝑥 Дані графіки утворюють стиском або розтягом графіка функції 𝑦 = 𝑓 𝑥 до осі 𝑂𝑥
- 4. ПРИГАДАЄМО // Найпростішіперетворення графіків функцій 𝑦 = 𝑓 𝑥 Частину графіка функції 𝑦 = 𝑓 𝑥 , що лежить нижче осі 𝑂𝑥, симетрично відображаємо відносно цієї осі Поясніть, як утворився графік функції 𝑦 = 𝑥 − 3 + 2 𝑦 = 2𝑥 − 2 𝑥 𝑦 𝑂 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 -1 -2 -3 -4 -5 -6 -7 -2 -3 𝑦 = 2𝑥 − 2 𝑥 𝑦 𝑂 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 -1 -2 -3 -4 -5 -6 -7 -8 -2 𝑦 = 𝑥 − 3 + 2 Поясніть, як побудувати графік функції 𝑦 = 2𝑥 − 2 Графік ф-ї 𝑦 = 𝑥 переносимо уздовж осі 𝑂𝑥 на 3 одиниці праворуч, а потім вздовж осі 𝑂𝑦 на 2 одиниці вгору
- 5. Побудуйте графік функції: 1)𝑦 = 3𝑥 − 2 2) 𝑦 = − 5 𝑥 3) 𝑦 = 𝑥2 − 2 4) 𝑦 = 𝑥2 − 2𝑥 𝑦 = 𝑥 𝑦 = 3𝑥 𝑦 = 3𝑥 − 2 𝑦 = 1 𝑥 𝑦 = 5 1 𝑥 𝑦 = − 5 𝑥 𝑦 = 𝑥2 𝑦 = 𝑥2 − 2 𝑦 = 𝑥2 − 2 𝑥в = − 𝑏 2𝑎 = − −2 2 = 1 𝑦в = 𝑓 𝑥в = 12 − 2 ∙ 1 = −1 𝑦 = 0 0 = 𝑥2 − 2𝑥 𝑥 𝑥 − 2 = 0 𝑥1 = 0 𝑥2 = 2 𝑂𝑥: 𝑥 = 0 𝑦 = 02 − 2 ∙ 0 𝑂𝑦: Точки перетину з осями координат: 𝑦 = 0 𝑎 > 0 → ∪ 1 Розвʼязуємо разом
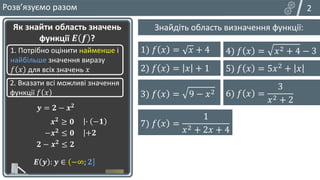
- 6. 4) 𝑦 =𝑎𝑥2 + 𝑏𝑥 + 𝑐 𝑥 𝑦 𝑥в 𝑦в 𝑥 𝑦 𝑥в 𝑦в 2 Розвʼязуємо разом Пригадайте, які обмеження мають такі функції: Як знайти область значень функції 𝑬 𝒇 ? 1. Потрібно оцінити найменше і найбільше значення виразу 𝑓 𝑥 для всіх значень 𝑥 2. Вказати всі можливі значення функції 𝑓 𝑥 𝒚 = 𝟐 − 𝒙𝟐 𝒙𝟐 ≥ 𝟎 𝑬 𝒚 : 𝒚 ∈ −∞; 𝟐 ∙ −𝟏 −𝒙𝟐 ≤ 𝟎 +𝟐 𝟐 − 𝒙𝟐 ≤ 𝟐 1) 𝑦 = 𝑥 2) 𝑦 = 𝑥2 3) 𝑦 = 𝑥 ≥ 0 ≥ 0 ≥ 0 𝑦в; ) +∞ −∞; 𝑦в Знайдіть область визначення функції: 1) 𝑓 𝑥 = 𝑥 + 4 2) 𝑓 𝑥 = 𝑥 + 1 3) 𝑓 𝑥 = 9 − 𝑥2 6) 𝑓 𝑥 = 3 𝑥2 + 2 4) 𝑓 𝑥 = 𝑥2 + 4 − 3 5) 𝑓 𝑥 = 5𝑥2 + 𝑥 7) 𝑓 𝑥 = 1 𝑥2 + 2𝑥 + 4
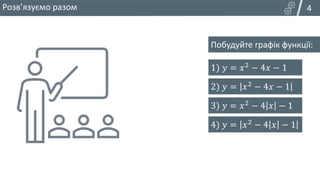
- 7. 3 Розвʼязуємо разом Дано функцію𝑓 𝑥 = − 𝑥 + 2, якщо 𝑥 > 2 𝑥2 − 1, якщо 𝑥 ≤ 2 Знайдіть 𝑓 2 , 𝑓 4 , 𝑓 0 , 𝑓 9
- 8. Побудуйте графік функції: 1)𝑦 = 𝑥2 − 4𝑥 − 1 2) 𝑦 = 𝑥2 − 4𝑥 − 1 3) 𝑦 = 𝑥2 − 4 𝑥 − 1 4) 𝑦 = 𝑥2 − 4 𝑥 − 1 𝒚 = 𝒙𝟐 − 𝟒𝒙 − 𝟏 𝒚 = 𝒙𝟐 − 𝟒𝒙 − 𝟏 𝒚 = 𝒙𝟐−࢞− 𝒚 = 𝒙𝟐 − 𝟒𝒙 − 𝟏 𝒚 = 𝒙𝟐 − 𝟒 𝒙 − 𝟏 𝒚 = 𝒙𝟐 − 𝟒𝒙 − 𝟏 𝒚 = 𝒙𝟐 − 𝟒 𝒙 − 𝟏 𝒚 = 𝒙𝟐 − 𝟒 𝒙 − 𝟏 4 Розвʼязуємо разом
- 9. Поясніть, як знайтиобласть визначення функції? Поясніть, як будувати графіки типу 𝑦 = 𝑓 𝑥 + 𝑛 і 𝑦 = 𝑓 𝑥 − 𝑛? Поясніть, як будувати графіки типу 𝑦 = 𝑓 𝑥 + 𝑚 і 𝑦 = 𝑓 𝑥 − 𝑚 ? Поясніть, як будувати графіки типу 𝑦 = −𝑓 𝑥 ? Поясніть, як будувати графіки типу 𝑦 = 𝑘𝑓 𝑥 ? Поясніть, як будувати графіки типу 𝑦 = 𝑓 𝑥 ? Відповідаємо
- 10. Бажаю творчих успіхів! 24.09.2023 Домашнєзавдання Повторити §1, опрацювати конспект Виконати № 1.17; 1.27; 1.32; 1.24 О.С. Істер Повторити П.1,опрацювати конспект Виконати № 1.24(2), 1.26(5-8), 1.28(2,3) А.Г. Мерзляк та ін.