solucionario de purcell 2

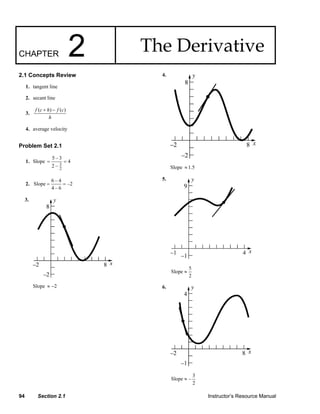
CHAPTER 2 The Derivative
2.1 Concepts Review 4.

1. tangent line

2. secant line

f (c + h ) − f ( c )
3.
h

4. average velocity

Problem Set 2.1

5–3
1. Slope = =4
2– 3
2 Slope ≈ 1.5

6–4 5.
2. Slope = = –2
4–6

3.

5
Slope ≈
2
Slope ≈ −2 6.

3
Slope ≈ –
2

94 Section 2.1 Instructor’s Resource Manual
© 2007 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they
currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.

7. y = x 2 + 1 [(2.01)3 − 1.0] − 7
d. msec =
2.01 − 2
a., b.
0.120601
=
0.01
= 12.0601

f (2 + h) – f (2)
e. mtan = lim
h →0 h
[(2 + h)3 – 1] – (23 − 1)
= lim
h →0 h
12h + 6h 2 + h3
= lim
h→0 h
h(12 + 6h + h 2 )
c. m tan = 2 = lim
h→0 h
(1.01)2 + 1.0 − 2 = 12
d. msec =
1.01 − 1 9. f (x) = x 2 – 1
0.0201
= f (c + h ) – f (c )
.01 mtan = lim
h→0 h
= 2.01
[(c + h)2 – 1] – (c 2 – 1)
= lim
f (1 + h) – f (1) h→0 h
e. mtan = lim
h →0 h c 2 + 2ch + h 2 – 1 – c 2 + 1
= lim
[(1 + h)2 + 1] – (12 + 1) h→0 h
= lim
h →0 h h(2c + h)
= lim = 2c
2 + 2h + h 2 − 2 h→0 h
= lim At x = –2, m tan = –4
h →0 h
h(2 + h) x = –1, m tan = –2
= lim x = 1, m tan = 2
h →0 h
= lim (2 + h) = 2 x = 2, m tan = 4
h →0
10. f (x) = x 3 – 3x
3
8. y = x – 1 f (c + h ) – f (c )
mtan = lim
h→0 h
a., b.
[(c + h)3 – 3(c + h)] – (c3 – 3c)
= lim
h→0 h
c3 + 3c 2 h + 3ch 2 + h3 – 3c – 3h – c3 + 3c
= lim
h→0 h
h(3c 2 + 3ch + h 2 − 3)
= lim = 3c 2 – 3
h→0 h
At x = –2, m tan = 9
x = –1, m tan = 0
x = 0, m tan = –3
x = 1, m tan = 0
c. m tan = 12 x = 2, m tan = 9

Instructor’s Resource Manual Section 2.1 95

11. 13. a. 16(12 ) –16(02 ) = 16 ft

b. 16(22 ) –16(12 ) = 48 ft

144 – 64
c. Vave = = 80 ft/sec
3–2

16(3.01) 2 − 16(3)2
d. Vave =
3.01 − 3
0.9616
=
0.01
1 = 96.16 ft/s
f ( x) =
x +1
f (1 + h) – f (1) e. f (t ) = 16t 2 ; v = 32c
mtan = lim v = 32(3) = 96 ft/s
h→0 h
1− 1
= lim 2+ h 2 (32 + 1) – (22 + 1)
h →0 h 14. a. Vave = = 5 m/sec
3– 2
− 2(2h h)
+
= lim [(2.003)2 + 1] − (22 + 1)
h →0 h b. Vave =
1 2.003 − 2
= lim − 0.012009
h→0 2(2 + h) =
1 0.003
=– = 4.003 m/sec
4
1 1
y – = – ( x –1) [(2 + h) 2 + 1] – (22 + 1)
2 4 Vave =
2+h–2
1 4h + h 2
12. f (x) = c. =
x –1 h
f (0 + h) − f (0) = 4 +h
mtan = lim
h →0 h
1 +1 d. f (t ) = t2 + 1
= lim h −1 f (2 + h) – f (2)
h →0 h v = lim
h →0 h
h
h −1 [(2 + h)2 + 1] – (22 + 1)
= lim
h →0
h = lim
h →0 h
1
= lim 4h + h 2
h →0 h − 1 = lim
h →0 h
= −1
y + 1 = –1(x – 0); y = –x – 1 = lim (4 + h)
h →0
=4


f (α + h) – f (α )
15. a. v = lim
h →0 h
2(α + h) + 1 – 2α + 1
= lim
h →0 h
2α + 2h + 1 – 2α + 1
= lim
h →0 h
( 2α + 2h + 1 – 2α + 1)( 2α + 2h + 1 + 2α + 1)
= lim
h →0 h( 2α + 2h + 1 + 2α + 1)
2h
= lim
h →0 h( 2α + 2h + 1 + 2α + 1)
2 1
= = ft/s
2α + 1 + 2α + 1 2α + 1

1 1
b. =
2α + 1 2
2α + 1 = 2
3
2 α + 1= 4; α =
2
The object reaches a velocity of 1 ft/s when t = 3 .
2 2

16. f (t ) = – t2 + 4 t 18. a. 1000(3)2 – 1000(2)2 = 5000
[–(c + h)2 + 4(c + h)] – (– c 2 + 4c)
v = lim
h →0 h 1000(2.5)2 – 1000(2)2 2250
b. = = 4500
– c 2 – 2ch – h 2 + 4c + 4h + c 2 – 4c 2.5 – 2 0.5
= lim
h →0 h
c. f (t ) = 1000t 2
h(–2c – h + 4)
= lim = –2c + 4 1000(2 + h)2 − 1000(2) 2
h →0 h r = lim
–2c + 4 = 0 when c = 2 h→0 h
The particle comes to a momentary stop at 4000 + 4000h + 1000h 2 – 4000
t = 2. = lim
h→0 h
h(4000 + 1000h)
⎡1 ⎤ ⎡1 2 ⎤ = lim = 4000
⎢ 2 (2.01) + 1⎥ – ⎢ 2 (2) + 1⎥ = 0.02005 g
2
17. a. h→0 h
⎣ ⎦ ⎣ ⎦
53 – 33 98
b. rave =
0.02005
= 2.005 g/hr 19. a. dave = = = 49 g/cm
2.01 – 2 5–3 2

1 2 b. f (x) = x 3
c. f (t ) = t +1
2 (3 + h)3 – 33
d = lim
⎡ 1 (2 + h)2 + 1⎤ – ⎡ 1 22 + 1⎤ h →0 h
r = lim ⎣ ⎦ ⎣2 ⎦
2
27 + 27h + 9h 2 + h3 – 27
h →0 h = lim
h→0 h
2 + 2h + 1 h 2 + 1 − 2 − 1
= lim 2
h(27 + 9h + h 2 )
h→0 h = lim = 27 g/cm
h→0 h
= lim
(
h 2+ 1 h
2 )=2
h→0 h
At t = 2, r = 2


R (c + h ) – R (c )
20. MR = lim
h→0 h
[0.4(c + h) – 0.001(c + h)2 ] – (0.4c – 0.001c 2 )
= lim
h→0 h
0.4c + 0.4h – 0.001c 2 – 0.002ch – 0.001h 2 – 0.4c + 0.001c 2
= lim
h→0 h
h(0.4 – 0.002c – 0.001h)
= lim = 0.4 – 0.002c
h→0 h
When n = 10, MR = 0.38; when n = 100, MR = 0.2

2(1 + h)2 – 2(1) 2 c. The building averages 84/7=12 feet from
21. a = lim floor to floor. Since the velocity is zero for
h →0 h
two intervals between time 0 and time 85, the
2 + 4h + 2h 2 – 2 elevator stopped twice. The heights are
= lim
h→0 h approximately 12 and 60. Thus, the elevator
h(4 + 2h) stopped at floors 1 and 5.
= lim =4
h→0 h 25. a. A tangent line at t = 91 has slope
approximately (63 − 48) /(91 − 61) = 0.5 . The
p (c + h ) – p (c )
22. r = lim normal high temperature increases at the rate
h→0 h
of 0.5 degree F per day.
[120(c + h)2 – 2(c + h)3 ] – (120c 2 – 2c3 )
= lim b. A tangent line at t = 191 has approximate
h →0 h
slope (90 − 88) / 30 ≈ 0.067 . The normal
h(240c – 6c 2 + 120h – 6ch – 2h 2 )
= lim high temperature increases at the rate of
h →0 h 0.067 degree per day.
= 240c – 6c 2 c. There is a time in January, about January 15,
When t = 10, r = 240(10) – 6(10) 2 = 1800 when the rate of change is zero. There is also
a time in July, about July 15, when the rate of
t = 20, r = 240(20) – 6(20)2 = 2400
change is zero.
t = 40, r = 240(40) – 6(40)2 = 0
d. The greatest rate of increase occurs around
day 61, that is, some time in March. The
100 – 800 175
23. rave = =– ≈ –29.167 greatest rate of decrease occurs between day
24 – 0 6 301 and 331, that is, sometime in November.
29,167 gal/hr
700 – 400 26. The slope of the tangent line at t = 1930 is
At 8 o’clock, r ≈ ≈ −75 approximately (8 − 6) /(1945 − 1930) ≈ 0.13 . The
6 − 10
75,000 gal/hr rate of growth in 1930 is approximately 0.13
million, or 130,000, persons per year. In 1990,
24. a. The elevator reached the seventh floor at time the tangent line has approximate slope
t = 80 . The average velocity is (24 − 16) /(20000 − 1980) ≈ 0.4 . Thus, the rate of
v avg = (84 − 0) / 80 = 1.05 feet per second growth in 1990 is 0.4 million, or 400,000,
persons per year. The approximate percentage
b. The slope of the line is approximately growth in 1930 is 0.107 / 6 ≈ 0.018 and in 1990 it
60 − 12 is approximately 0.4 / 20 ≈ 0.02 .
= 1.2 . The velocity is
55 − 15
27. In both (a) and (b), the tangent line is always
approximately 1.2 feet per second.
positive. In (a) the tangent line becomes steeper
and steeper as t increases; thus, the velocity is
increasing. In (b) the tangent line becomes flatter
and flatter as t increases; thus, the velocity is
decreasing.


1 2.2 Concepts Review
28. f (t ) = t 3 + t
3
f (c + h) – f (c) f (t ) – f (c)
f ( c + h ) – f (c ) 1. ;
current = lim h t –c
h →0 h
⎡
= lim ⎣
(
1 ( c + h )3 + ( c + h ) ⎤ – 1 c 3 + c
3 ⎦ 3 ) 2. f ′(c )
h→0 h

= lim
(
h c 2 + ch + 1 h 2 + 1
3 ) = c2 + 1 3. continuous; f ( x) = x

h→0 h dy
When t = 3, the current =10 4. f '( x);
dx
c 2 + 1 = 20
2
c = 19
Problem Set 2.2
c = 19 ≈ 4.4
A 20-amp fuse will blow at t = 4.4 s.
f (1 + h) – f (1)
1. f ′(1) = lim
h →0 h
29. A = πr 2 , r = 2t
(1 + h)2 – 12 2h + h 2
A = 4πt2 = lim = lim
h→0 h h →0 h
4π(3 + h)2 – 4π(3)2
rate = lim = lim (2 + h ) = 2
h →0 h h→0
h(24π + 4πh)
= lim = 24π km2/day f (2 + h) – f (2)
h→0 h 2. f ′(2) = lim
h →0 h
4 1 [2(2 + h)]2 – [2(2)]2
30. V = π r 3 , r = t = lim
3 4 h→0 h
1
V = π t3 16h + 4h 2
48 = lim = lim (16 + 4h) = 16
h→0 h h →0
1 (3 + h)3 − 33 27
rate = π lim = π f (3 + h) – f (3)
48 h→0 h 48 3. f ′(3) = lim
9 h →0 h
= π inch 3 / sec
16 [(3 + h)2 – (3 + h)] – (32 – 3)
= lim
h→0 h
31. y = f ( x) = x 3 – 2 x 2 + 1 5h + h 2
= lim = lim (5 + h) = 5
h→0 h h →0
a. m tan = 7 b. m tan = 0
f (4 + h) – f (4)
c. m tan = –1 d. m tan = 17. 92 4. f ′(4) = lim
h →0 h
3–(3+ h )
32. y = f ( x) = sin x sin 2 x 2 1
3+ h
1
– 4–1 3(3+ h ) –1
= lim = lim = lim
h →0 h h →0 h h →0 3(3 + h)
a. m tan = –1.125 b. m tan ≈ –1.0315
1
=–
c. m tan = 0 d. m tan ≈ 1.1891
9

s ( x + h) – s ( x )
33. s = f (t ) = t + t cos 2 t 5. s ′( x) = lim
h →0 h
At t = 3, v ≈ 2.818 [2( x + h) + 1] – (2 x + 1)
= lim
h →0 h
(t + 1)3
34. s = f (t ) = 2h
t+2 = lim =2
h →0 h
At t = 1.6, v ≈ 4.277


f ( x + h) – f ( x ) g ( x + h) – g ( x )
6. f ′( x) = lim 12. g ′( x) = lim
h →0 h h →0 h
[α ( x + h) + β ] – (α x + β ) [( x + h)4 + ( x + h) 2 ] – ( x 4 + x 2 )
= lim = lim
h →0 h h →0 h
αh 4hx3 + 6h 2 x 2 + 4h3 x + h 4 + 2hx + h 2
= lim =α = lim
h →0 h
h →0 h
r ( x + h) – r ( x ) = lim (4 x3 + 6hx 2 + 4h 2 x + h3 + 2 x + h)
7. r ′( x) = lim h →0
h →0 h 3
= 4x + 2x
[3( x + h)2 + 4] – (3 x 2 + 4)
= lim h( x + h) – h( x )
h →0 h 13. h′( x) = lim
h →0 h
6 xh + 3h 2
= lim = lim (6 x + 3h) = 6 x ⎡⎛ 2 2 ⎞ 1⎤
h →0 h h →0 = lim ⎢⎜ – ⎟⋅ ⎥
h → 0 ⎣⎝ x + h x ⎠ h ⎦
f ( x + h) – f ( x ) ⎡ –2h 1 ⎤
8. f ′( x) = lim = lim ⎢ ⋅ ⎥ = lim
–2
=–
2
h →0 h h → 0 ⎣ x ( x + h ) h ⎦ h →0 x ( x + h ) x2
[( x + h)2 + ( x + h) + 1] – ( x 2 + x + 1)
= lim
h →0 h S ( x + h) – S ( x )
14. S ′( x) = lim
2 xh + h + h
2 h →0 h
= lim = lim (2 x + h + 1) = 2 x + 1
h →0 h h →0 ⎡⎛ 1 1 ⎞ 1⎤
= lim ⎢⎜ – ⎟⋅ ⎥
h →0 ⎣⎝ x + h + 1 x + 1 ⎠ h ⎦
f ( x + h) – f ( x ) ⎡
9. f ′( x) = lim –h 1⎤
h →0 h = lim ⎢ ⋅ ⎥
h→0 ⎣ ( x + 1)( x + h + 1) h ⎦
[a( x + h) 2 + b( x + h) + c] – (ax 2 + bx + c)
= lim = lim
–1
=−
1
h →0 h
h→0 ( x + 1)( x + h + 1) ( x + 1) 2
2axh + ah 2 + bh
= lim = lim (2ax + ah + b)
h →0 h h →0 F ( x + h) – F ( x )
= 2ax + b 15. F ′( x) = lim
h →0 h
f ( x + h) – f ( x ) ⎡⎛ 6 6 ⎞ 1⎤
10. f ′( x) = lim = lim ⎢⎜ – ⎟⋅ ⎥
h →0 h →0 ⎢⎜ ( x + h) 2 + 1 x 2 + 1 ⎟ h ⎥
h ⎣⎝ ⎠ ⎦
( x + h) 4 – x 4 ⎡ 6( x + 1) – 6( x + 2hx + h 2 + 1) 1 ⎤
2 2
= lim = lim ⎢ ⋅ ⎥
h →0 h h→0 ⎢ ( x 2 + 1)( x 2 + 2hx + h 2 + 1)
⎣ h⎥
⎦
4hx3 + 6h 2 x 2 + 4h3 x + h 4
= lim ⎡ –12hx – 6h 2
1 ⎤
h →0 h = lim ⎢ ⋅ ⎥
h→0 ⎢ ( x 2 + 1)( x 2 + 2hx + h 2 + 1) h ⎥
= lim (4 x3 + 6hx 2 + 4h 2 x + h3 ) = 4 x3 ⎣ ⎦
h →0 –12 x – 6h 12 x
= lim =−
f ( x + h) – f ( x )
h →0 ( x 2 + 1)( x + 2hx + h + 1)
2 2
( x + 1)2
2
11. f ′( x) = lim
h →0 h
F ( x + h) – F ( x )
[( x + h)3 + 2( x + h)2 + 1] – ( x3 + 2 x 2 + 1) 16. F ′( x) = lim
= lim h →0 h
h →0 h
⎡⎛ x + h –1 x –1 ⎞ 1 ⎤
3hx 2 + 3h 2 x + h3 + 4hx + 2h 2 = lim ⎢⎜ – ⎟⋅ ⎥
= lim h →0 ⎣ ⎝ x + h + 1 x + 1 ⎠ h ⎦
h →0 h
⎡ x 2 + hx + h –1 – ( x 2 + hx – h –1) 1 ⎤
= lim (3x + 3hx + h + 4 x + 2h) = 3 x + 4 x
2 2 2 = lim ⎢ ⋅ ⎥
h →0 h →0 ⎢
⎣ ( x + h + 1)( x + 1) h⎥⎦
⎡ 2h 1⎤ 2
= lim ⎢ ⋅ ⎥=
h→0 ⎣ ( x + h + 1)( x + 1) h ⎦ ( x + 1) 2


G ( x + h) – G ( x )
17. G ′( x ) = lim
h →0 h
⎡⎛ 2( x + h) –1 2 x –1 ⎞ 1 ⎤
= lim ⎢⎜ ⎟⋅
x – 4 ⎠ h⎥
–
h→0 ⎣⎝ x + h – 4 ⎦
⎡ 2 x 2 + 2hx − 9 x − 8h + 4 − (2 x 2 + 2hx − 9 x − h + 4) 1 ⎤ ⎡ –7h 1⎤
= lim ⎢ ⋅ ⎥ = lim ⎢ ⋅ ⎥
h →0 ⎢
⎣ ( x + h − 4)( x − 4) h⎥
⎦ h→0 ⎣ ( x + h – 4)( x – 4) h ⎦
–7 7
= lim =–
h→0 ( x + h – 4)( x – 4) ( x – 4)2

G ( x + h) – G ( x )
18. G ′( x ) = lim
h →0 h
⎡⎛ 2( x + h) 2x ⎞ 1 ⎤ ⎡ (2 x + 2h)( x 2 – x ) – 2 x( x 2 + 2 xh + h 2 – x – h) 1 ⎤
= lim ⎢⎜ – ⎟ ⋅ ⎥ = lim ⎢ ⋅ ⎥
⎜ ⎟
h →0 ⎢⎝ ( x + h) 2 – ( x + h) x 2 – x ⎠ h ⎥ ( x 2 + 2hx + h 2 – x – h)( x 2 – x)
⎣ ⎦ h→0 ⎢⎣ h⎥⎦
⎡ 2
–2h x – 2hx 2
1⎤
= lim ⎢ ⋅ ⎥
h→0 ⎢ ( x + 2hx + h – x – h)( x – x ) h ⎥
⎣
2 2 2
⎦
–2hx – 2 x 2
= lim
h→0 ( x 2 + 2hx + h 2 – x – h)( x 2 – x)
–2 x 2 2
= =–
2 2
( x – x) ( x – 1) 2

g ( x + h) – g ( x )
19. g ′( x) = lim
h →0 h
3( x + h) – 3x
= lim
h→0 h
( 3x + 3h – 3x )( 3x + 3h + 3 x )
= lim
h→0 h( 3 x + 3h + 3x )
3h 3 3
= lim = lim =
h→0 h( 3 x + 3h + 3 x ) h →0 3x + 3h + 3x 2 3x

g ( x + h) – g ( x )
20. g ′( x) = lim
h →0 h
⎡⎛ 1 1 ⎞ 1⎤
= lim ⎢⎜ – ⎟⋅ ⎥
h→0 ⎢⎜ 3( x + h) 3x ⎟ h ⎥
⎣⎝ ⎠ ⎦
⎡ 3x – 3x + 3h 1 ⎤
= lim ⎢ ⋅ ⎥
h→0 ⎢
⎣ 9 x ( x + h) h⎥
⎦
⎡ ( 3 x – 3 x + 3h )( 3 x + 3 x + 3h ) 1 ⎤
= lim ⎢ ⋅ ⎥
h→0 ⎢
⎣ 9 x( x + h)( 3x + 3x + 3h ) h⎥⎦
–3h –3 1
= lim = =–
h→0 h 9 x( x + h)( 3x + 3x + 3h ) 3x ⋅ 2 3x 2 x 3x


H ( x + h) – H ( x )
21. H ′( x ) = lim
h →0 h
⎡⎛ 3 3 ⎞ 1⎤
= lim ⎢⎜ – ⎟⋅ ⎥
h→0 ⎣⎝ x + h – 2 x – 2 ⎠ h⎦
⎡3 x – 2 – 3 x + h – 2 1 ⎤
= lim ⎢ ⋅ ⎥
⎣ ( x + h – 2)( x – 2) h ⎥
h→0 ⎢ ⎦
3( x – 2 – x + h – 2)( x – 2 + x + h – 2)
= lim
h→0 h ( x + h – 2)( x – 2)( x – 2 + x + h – 2)
−3h
= lim
h→0 h[( x – 2) x + h – 2 + ( x + h – 2) x – 2]
–3
= lim
h→0 ( x – 2) x + h – 2 + ( x + h – 2) x – 2
3 3
=– =−
2( x – 2) x – 2 2( x − 2)3 2

H ( x + h) – H ( x )
22. H ′( x) = lim
h →0 h
( x + h) 2 + 4 – x 2 + 4
= lim
h→0 h
⎛ x 2 + 2hx + h 2 + 4 – x 2 + 4 ⎞ ⎛ x 2 + 2hx + h 2 + 4 + x 2 + 4 ⎞
⎜ ⎟⎜ ⎟
= lim ⎝ ⎠⎝ ⎠
h →0
h⎜⎛ x 2 + 2hx + h 2 + 4 + x 2 + 4 ⎞
⎟
⎝ ⎠
2hx + h 2
= lim
h→0
h ⎛ x 2 + 2hx + h 2 + 4 + x 2 + 4 ⎞
⎜ ⎟
⎝ ⎠
2x + h
= lim
h →0 x 2 + 2hx + h 2 + 4 + x 2 + 4
2x x
= =
2 x +4
2
x +4
2

f (t ) – f ( x) f (t ) – f ( x)
23. f ′( x) = lim 24. f ′( x) = lim
t→x t–x t→x t–x
(t − 3t ) – ( x – 3 x)
2 2
(t + 5t ) – ( x3 + 5 x)
3
= lim = lim
t 2 – x 2 – (3t – 3x) t 3 – x3 + 5t – 5 x
= lim = lim
(t – x)(t + x) – 3(t – x) (t – x)(t 2 + tx + x 2 ) + 5(t – x)
= lim = lim
(t – x)(t + x – 3) (t – x)(t 2 + tx + x 2 + 5)
= lim = lim (t + x – 3) = lim
t→x t–x t→x
t→x t–x
=2x–3
= lim (t 2 + tx + x 2 + 5) = 3x 2 + 5
t→x


f (t ) – f ( x) 38. The slope of the tangent line is always −1 .
25. f ′( x) = lim
t→x t–x
⎡⎛ t x ⎞ ⎛ 1 ⎞⎤
= lim ⎢⎜ – ⎟⎜ ⎟⎥
t → x ⎣⎝ t – 5 x – 5 ⎠ ⎝ t – x ⎠ ⎦
tx – 5t – tx + 5 x
= lim
t → x (t – 5)( x – 5)(t – x)
–5(t – x) –5
= lim = lim
t → x (t – 5)( x – 5)(t – x) t → x (t – 5)( x – 5)
5 39. The derivative is positive until x = 0 , then
=− becomes negative.
( x − 5)
2

f (t ) – f ( x)
26. f ′( x) = lim
t→x t–x
⎡⎛ t + 3 x + 3 ⎞ ⎛ 1 ⎞ ⎤
= lim ⎢⎜ ⎟⎜ ⎟
x ⎠ ⎝ t – x ⎠⎥
–
t → x ⎣⎝ t ⎦
3x – 3t –3 3
= lim = lim =–
t → x xt (t – x ) t → x xt x2
40. The derivative is negative until x = 1 , then
27. f (x) = 2 x 3 at x = 5 becomes positive.
28. f (x) = x 2 + 2 x at x = 3

29. f (x) = x 2 at x = 2

30. f (x) = x 3 + x at x = 3

31. f (x) = x 2 at x

32. f (x) = x 3 at x 41. The derivative is −1 until x = 1 . To the right of
x = 1 , the derivative is 1. The derivative is
2 undefined at x = 1 .
33. f (t ) = at t
t

34. f(y) = sin y at y

35. f(x) = cos x at x

36. f(t) = tan t at t

37. The slope of the tangent line is always 2.
42. The derivative is −2 to the left of x = −1 ; from
−1 to 1, the derivative is 2, etc. The derivative is
not defined at x = −1, 1, 3 .


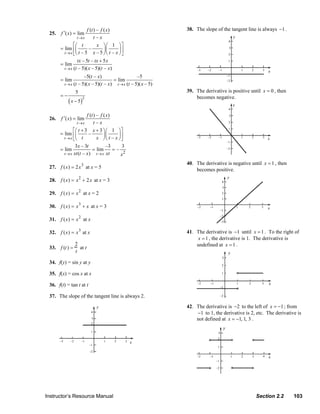
43. The derivative is 0 on ( −3, −2 ) , 2 on ( −2, −1) , 0 1
Δy x +Δx +1 – x +1
1
53. =
on ( −1, 0 ) , −2 on ( 0,1) , 0 on (1, 2 ) , 2 on ( 2,3) Δx Δx
and 0 on ( 3, 4 ) . The derivative is undefined at ⎛ x + 1 – ( x + Δx + 1) ⎞ ⎛ 1 ⎞
=⎜ ⎟⎜ ⎟
x = −2, − 1, 0, 1, 2, 3 . ⎝ ( x + Δx + 1)( x + 1) ⎠ ⎝ Δx ⎠
– Δx
=
( x + Δx + 1)( x + 1)Δx
1
=–
( x + Δx + 1)( x + 1)
dy ⎡ 1 ⎤ 1
= lim − =−
dx Δx →0 ⎢ ( x + Δx + 1)( x + 1) ⎥
⎣ ⎦ ( x + 1) 2

1 ⎛ 1⎞
1+ − ⎜1 + ⎟
44. The derivative is 1 except at x = −2, 0, 2 where Δy x + Δx ⎝ x ⎠
54. =
it is undefined. Δx Δx
1 1 −Δx
− x ( x + Δx )
= x + Δx x =
1
=−
Δx Δx x ( x + Δx )
dy 1 1
= lim − =− 2
dx Δx →0 x ( x + Δx ) x

55.
x + Δx − 1 x − 1
−
45. Δy = [3(1.5) + 2] – [3(1) + 2] = 1.5 Δy x + Δx + 1 x + 1
=
Δx Δx
46. Δy = [3(0.1) 2 + 2(0.1) + 1] – [3(0.0) 2 + 2(0.0) + 1] ( x + 1)( x + Δx − 1) − ( x − 1)( x + Δx + 1) 1
= ×
= 0.23 ( x + Δx + 1)( x + 1) Δx

47. Δy = 1/1.2 – 1/1 = – 0.1667 x 2 + xΔx − x + x + Δx − 1 − ⎡ x 2 + xΔx − x + x − Δx − 1⎤ 1
= ⎣ ⎦×
x + x Δx + x + x + Δ x + 1
2 Δx
48. Δy = 2/(0.1+1) – 2/(0+1) = – 0.1818
2Δx 1 2
= 2 × =
3 3 x + xΔx + x + x + Δx + 1 Δx x 2 + xΔx + x + x + Δx + 1
49. Δy = – ≈ 0.0081
2.31 + 1 2.34 + 1 dy
= lim
2
=
2
=
2
dx Δx →0 x 2 + xΔx + x + x + Δx + 1 x 2 + 2 x + 1 ( x + 1)2
50. Δy = cos[2(0.573)] – cos[2(0.571)] ≈ –0.0036

Δy ( x + Δx) 2 – x 2 2 xΔx + (Δx) 2
51. = = = 2 x + Δx ( x + Δx ) 2 − 1 − x 2 − 1
Δx Δx Δx Δy
56. = x + Δx x
dy Δx Δx
= lim (2 x + Δx) = 2 x
dx Δx →0
(
⎡ x ( x + Δx )2 − x − ( x + Δx ) x 2 − 1 ⎤
=⎢
)
⎥× 1
⎢ x ( x + Δx ) ⎥ Δx
Δy [( x + Δx)3 – 3( x + Δx) 2 ] – ( x3 – 3 x 2 ) ⎣ ⎦
52. =
Δx Δx
( ( )) (
⎡ x x + 2 xΔx + Δx − x − x + x 2 Δx − x − Δx
=⎢
2 2 3
)⎤× 1
⎥
3 x 2 Δx + 3x(Δx)2 – 6 xΔx – 3(Δx) 2 + Δx3 ⎢ x 2 + x Δx ⎥ Δx
= ⎢
⎣ ⎥
⎦
Δx
x 2 Δx + x ( Δx ) + Δx
2
= 3x 2 + 3xΔx – 6 x – 3Δx + (Δx)2 1 x 2 + x Δx + 1
= × = 2
x + x Δx
2 Δx x + x Δx
dy
= lim (3 x 2 + 3 xΔx – 6 x – 3Δx + (Δx)2 ) dy x 2 + xΔx + 1 x 2 + 1
dx Δx→0 = lim = 2
dx Δx → 0 x 2 + xΔx x
= 3x2 – 6 x


1 63. The derivative is 0 at approximately t = 15 and
57. f ′(0) ≈ – ; f ′(2) ≈ 1 t = 201 . The greatest rate of increase occurs at
2
2 about t = 61 and it is about 0.5 degree F per day.
f ′(5) ≈ ; f ′(7) ≈ –3 The greatest rate of decrease occurs at about
3
t = 320 and it is about 0.5 degree F per day. The
58. g ′(–1) ≈ 2; g ′(1) ≈ 0 derivative is positive on (15,201) and negative on
(0,15) and (201,365).
1
g ′(4) ≈ –2; g ′(6) ≈ –
3

59.

64. The slope of a tangent line for the dashed
function is zero when x is approximately 0.3 or
1.9. The solid function is zero at both of these
points. The graph indicates that the solid
function is negative when the dashed function
60. has a tangent line with a negative slope and
positive when the dashed function has a tangent
line with a positive slope. Thus, the solid
function is the derivative of the dashed function.

65. The short-dash function has a tangent line with
zero slope at about x = 2.1 , where the solid
function is zero. The solid function has a tangent
line with zero slope at about x = 0.4, 1.2 and 3.5.
The long-dash function is zero at these points.
5 3 The graph shows that the solid function is
61. a. f (2) ≈ ; f ′(2) ≈ positive (negative) when the slope of the tangent
2 2 line of the short-dash function is positive
f (0.5) ≈ 1.8; f ′(0.5) ≈ –0.6 (negative). Also, the long-dash function is
2.9 − 1.9 positive (negative) when the slope of the tangent
b. = 0.5 line of the solid function is positive (negative).
2.5 − 0.5 Thus, the short-dash function is f, the solid
c. x=5 function is f ' = g , and the dash function is g ' .
d. x = 3, 5
66. Note that since x = 0 + x, f(x) = f(0 + x) = f(0)f(x),
e. x = 1, 3, 5 hence f(0) = 1.
f. x=0 f ( a + h) – f ( a )
f ′(a ) = lim
h →0 h
3
g. x ≈ −0.7, and 5 < x < 7 f ( a ) f ( h) – f ( a )
2 = lim
h→0 h
62. The derivative fails to exist at the corners of the f ( h) – 1 f (h) – f (0)
graph; that is, at t = 10, 15, 55, 60, 80 . The = f (a ) lim = f (a) lim
h →0 h h →0 h
derivative exists at all other points on the interval = f (a ) f ′(0)
(0,85) . f ′ ( a) exists since f ′ (0 ) exists.


67. If f is differentiable everywhere, then it is b. If f is an even function,
continuous everywhere, so f (t ) − f ( x0 )
lim − f ( x ) = lim− ( mx + b ) = 2 m + b = f (2) = 4 f ′(– x0 ) = lim . Let u = –t, as
x→2 x→ 2 t →− x0 t + x0
and b = 4 – 2m. f (−u ) − f ( x0 )
For f to be differentiable everywhere, above, then f ′(− x0 ) = lim
u → x0 −u + x0
f ( x) − f (2)
f ′(2) = lim must exist. f (u ) − f ( x0 ) f (u ) − f ( x0 )
x→2 x−2 = lim = − lim
u → x0 −(u − x0 ) u → x0 u − x0
f ( x) − f (2) x2 − 4
lim = lim = lim ( x + 2) = 4 = − f ′ (x 0 ) = −m.
x → 2+ x−2 x → 2+ x − 2 x → 2+
f ( x) − f (2) mx + b − 4 70. Say f(–x) = –f(x). Then
lim = lim
− x−2 − x−2 f (– x + h) – f (– x)
x→2 x→2 f ′(– x) = lim
mx + 4 − 2m − 4 m( x − 2) h →0 h
= lim = lim =m – f ( x – h) + f ( x ) f ( x – h) – f ( x )
x → 2− x−2 x →2 − x−2 = lim = – lim
h→0 h h →0 h
Thus m = 4 and b = 4 – 2(4) = –4
f [ x + (– h)] − f ( x)
= lim = f ′( x) so f ′ ( x ) is
f ( x + h) – f ( x ) + f ( x ) – f ( x – h ) – h →0 –h
68. f s ( x) = lim
h →0 2h an even function if f(x) is an odd function.
⎡ f ( x + h ) – f ( x ) f ( x – h) – f ( x ) ⎤ Say f(–x) = f(x). Then
= lim ⎢ + ⎥ f (– x + h) – f (– x)
h→0 ⎣ 2h –2h ⎦ f ′(– x) = lim
h →0 h
1 f ( x + h) – f ( x ) 1 f [ x + (– h)] – f ( x)
= lim + lim f ( x – h) – f ( x )
2 h →0 h 2 – h →0 –h = lim
h→0 h
1 1
= f ′( x) + f ′( x ) = f ′( x). f [ x + (– h)] – f ( x)
2 2 = – lim = – f ′( x) so f ′ (x)
For the converse, let f (x) = x . Then – h→0 –h
is an odd function if f(x) is an even function.
h – –h h–h
f s (0) = lim = lim =0
h→0 2h h →0 2h 71.
but f ′ (0) does not exist.

f (t ) − f ( x0 )
69. f ′( x0 ) = lim , so
t→x
0
t − x0
f (t ) − f (− x0 )
f ′(− x0 ) = lim
t →− x t − (− x0 )
0 8 ⎛ 8⎞
a. 0< x< ; ⎜ 0, ⎟
f (t ) − f (− x0 ) 3 ⎝ 3⎠
= lim
t →− x 0 t + x0
8 ⎡ 8⎤
b. 0≤ x≤ ; 0,
a. If f is an odd function, 3 ⎢ 3⎥
⎣ ⎦
f (t ) − [− f (− x0 )]
f ′(− x0 ) = lim
t →− x0 t + x0 c. A function f(x) decreases as x increases when
f ′ ( x ) < 0.
f (t ) + f (− x0 )
= lim .
t →− x0 t + x0 72.
Let u = –t. As t → − x0 , u → x 0 and so
f (−u ) + f ( x0 )
f ′(− x0 ) = lim
u → x0 −u + x0
− f (u ) + f ( x0 ) −[ f (u ) − f ( x0 )]
= lim = lim
u → x0 −(u − x0 ) u → x0 −(u − x0 )
f (u ) − f ( x0 ) a. π < x < 6.8 b. π < x < 6.8
= lim = f ′( x0 ) = m.
u → x0 u − x0
c. A function f(x) increases as x increases when
f ′ ( x ) > 0.


2.3 Concepts Review 13. Dx ( x 4 + x3 + x 2 + x + 1)
1. the derivative of the second; second; = Dx ( x 4 ) + Dx ( x3 ) + Dx ( x 2 ) + Dx ( x) + Dx (1)
f (x) g′ (x ) + g(x) f ′( x)
= 4 x3 + 3 x 2 + 2 x + 1
2. denominator; denominator; square of the
g ( x) f ′( x) – f ( x) g ′( x) 14. Dx (3x 4 – 2 x3 – 5 x 2 + πx + π2 )
denominator;
g 2 ( x) = 3Dx ( x 4 ) – 2 Dx ( x3 ) – 5Dx ( x 2 )

n– 1 n –1
+ πDx ( x) + Dx (π2 )
3. nx h ; nx
= 3(4 x3 ) – 2(3 x 2 ) – 5(2 x) + π(1) + 0
4. kL(f); L(f) + L(g); Dx
= 12 x3 – 6 x 2 –10 x + π

Problem Set 2.3 15. Dx (πx 7 – 2 x5 – 5 x –2 )
= πDx ( x7 ) – 2 Dx ( x5 ) – 5 Dx ( x –2 )
1. Dx (2 x ) = 2 Dx ( x ) = 2 ⋅ 2 x = 4 x
2 2
= π(7 x6 ) – 2(5 x 4 ) – 5(–2 x –3 )

2. Dx (3x3 ) = 3Dx ( x3 ) = 3 ⋅ 3x 2 = 9 x 2 = 7 πx 6 –10 x 4 + 10 x –3

3. Dx (πx ) = πDx ( x) = π ⋅1 = π 16. Dx ( x12 + 5 x −2 − πx −10 )
= Dx ( x12 ) + 5Dx ( x −2 ) − πDx ( x −10 )
4. Dx (πx ) = πDx ( x ) = π ⋅ 3 x = 3πx
3 3 2 2
= 12 x11 + 5(−2 x −3 ) − π(−10 x −11 )

5. Dx (2 x –2 ) = 2 Dx ( x –2 ) = 2(–2 x –3 ) = –4 x –3 = 12 x11 − 10 x −3 + 10πx −11

⎛ 3 ⎞
6. Dx (–3 x –4 ) = –3Dx ( x –4 ) = –3(–4 x –5 ) = 12 x –5 17. Dx ⎜ + x –4 ⎟ = 3Dx ( x –3 ) + Dx ( x –4 )
3
⎝x ⎠
⎛π⎞ = 3(–3 x –4 ) + (–4 x –5 ) = –
9
– 4 x –5
7. Dx ⎜ ⎟ = πDx ( x –1 ) = π(–1x –2 ) = – πx –2
⎝x⎠ x4
π
=– 2
x 18. Dx (2 x –6 + x –1 ) = 2 Dx ( x –6 ) + Dx ( x –1 )
= 2(–6 x –7 ) + (–1x –2 ) = –12 x –7 – x –2
⎛α ⎞
8. Dx ⎜ ⎟ = α Dx ( x –3 ) = α (–3x –4 ) = –3α x –4
⎝ x3 ⎠ ⎛2 1 ⎞
⎟ = 2 Dx ( x ) – Dx ( x )
–1 –2
19. Dx ⎜ –
3α ⎝ x x2 ⎠
=–
x4 2 2
= 2(–1x –2 ) – (–2 x –3 ) = – +
2
x x3
⎛ 100 ⎞
9. Dx ⎜ = 100 Dx ( x –5 ) = 100(–5 x –6 )
5 ⎟
⎝ x ⎠ ⎛ 3 1 ⎞
⎟ = 3 Dx ( x ) – Dx ( x )
–3 –4
20. Dx ⎜ –
500 ⎝x 3
x4 ⎠
= –500 x –6 = –
x6 9 4
= 3(–3 x –4 ) – (–4 x –5 ) = – +
4
x x5
⎛ 3α ⎞ 3α 3α
10. Dx ⎜ = Dx ( x –5 ) = (–5 x –6 )
5⎟
⎝ 4x ⎠ 4 4 ⎛ 1 ⎞ 1
21. Dx ⎜ + 2 x ⎟ = Dx ( x –1 ) + 2 Dx ( x)
15α –6 15α ⎝ 2x ⎠ 2
=– x =–
4 4 x6 1 1
= (–1x –2 ) + 2(1) = – +2
2 2 x2
11. Dx ( x 2 + 2 x) = Dx ( x 2 ) + 2 Dx ( x ) = 2 x + 2

12. Dx (3x 4 + x3 ) = 3Dx ( x 4 ) + Dx ( x3 )
= 3(4 x3 ) + 3x 2 = 12 x3 + 3 x 2


⎛ 2 2⎞ 2 ⎛2⎞ 26. Dx [(–3 x + 2)2 ]
22. Dx ⎜ – ⎟ = Dx ( x –1 ) – Dx ⎜ ⎟
⎝ 3x 3 ⎠ 3 ⎝3⎠ = (–3 x + 2) Dx (–3 x + 2) + (–3 x + 2) Dx (–3x + 2)
2 2 = (–3x + 2)(–3) + (–3x + 2)(–3) = 18x – 12
= (–1x –2 ) – 0 = –
3 3x 2
27. Dx [( x 2 + 2)( x3 + 1)]
23. Dx [ x( x 2 + 1)] = x Dx ( x 2 + 1) + ( x 2 + 1) Dx ( x) = ( x 2 + 2) Dx ( x3 + 1) + ( x3 + 1) Dx ( x 2 + 2)
= x(2 x) + ( x + 1)(1) = 3 x + 1
2 2
= ( x 2 + 2)(3x 2 ) + ( x3 + 1)(2 x)
= 3x 4 + 6 x 2 + 2 x 4 + 2 x
24. Dx [3 x( x3 –1)] = 3 x Dx ( x3 –1) + ( x3 –1) Dx (3 x)
= 5x4 + 6 x2 + 2 x
= 3x(3 x 2 ) + ( x3 –1)(3) = 12 x3 – 3
28. Dx [( x 4 –1)( x 2 + 1)]
25. Dx [(2 x + 1) ] 2
= ( x 4 –1) Dx ( x 2 + 1) + ( x 2 + 1) Dx ( x 4 –1)
= (2 x + 1) Dx (2 x + 1) + (2 x + 1) Dx (2 x + 1)
= (2 x + 1)(2) + (2 x + 1)(2) = 8 x + 4 = ( x 4 –1)(2 x) + ( x 2 + 1)(4 x3 )
= 2 x5 – 2 x + 4 x5 + 4 x3 = 6 x 5 + 4 x3 – 2 x

29. Dx [( x 2 + 17)( x3 – 3 x + 1)]
= ( x 2 + 17) Dx ( x3 – 3 x + 1) + ( x3 – 3x + 1) Dx ( x 2 + 17)
= ( x 2 + 17)(3 x 2 – 3) + ( x3 – 3x + 1)(2 x)
= 3x 4 + 48 x 2 – 51 + 2 x 4 – 6 x 2 + 2 x
= 5 x 4 + 42 x 2 + 2 x – 51

30. Dx [( x 4 + 2 x)( x3 + 2 x 2 + 1)] = ( x 4 + 2 x) Dx ( x3 + 2 x 2 + 1) + ( x3 + 2 x 2 + 1) Dx ( x 4 + 2 x)
= ( x 4 + 2 x)(3 x 2 + 4 x) + ( x3 + 2 x 2 + 1)(4 x3 + 2)
= 7 x6 + 12 x5 + 12 x3 + 12 x 2 + 2

31. Dx [(5 x 2 – 7)(3x 2 – 2 x + 1)] = (5 x 2 – 7) Dx (3x 2 – 2 x + 1) + (3x 2 – 2 x + 1) Dx (5 x 2 – 7)
= (5 x 2 – 7)(6 x – 2) + (3 x 2 – 2 x + 1)(10 x)
= 60 x3 – 30 x 2 – 32 x + 14

32. Dx [(3 x 2 + 2 x)( x 4 – 3 x + 1)] = (3 x 2 + 2 x) Dx ( x 4 – 3 x + 1) + ( x 4 – 3 x + 1) Dx (3x 2 + 2 x)
= (3 x 2 + 2 x)(4 x3 – 3) + ( x 4 – 3 x + 1)(6 x + 2)
= 18 x5 + 10 x 4 – 27 x 2 – 6 x + 2

⎛ 1 ⎞ (3x 2 + 1) Dx (1) – (1) Dx (3 x 2 + 1)
33. Dx ⎜ ⎟=
⎝ 3x2 + 1 ⎠ (3 x 2 + 1)2
(3 x 2 + 1)(0) – (6 x) 6x
= =–
(3 x + 1)
2 2
(3x + 1) 2
2

⎛ 2 ⎞ (5 x 2 –1) Dx (2) – (2) Dx (5 x 2 –1)
34. Dx ⎜ ⎟=
⎝ 5 x 2 –1 ⎠ (5 x 2 –1) 2
(5 x 2 –1)(0) – 2(10 x) 20 x
= =–
2 2
(5 x –1) (5 x 2 –1)2


⎛ 1 ⎞ (4 x 2 – 3x + 9) Dx (1) – (1) Dx (4 x 2 – 3 x + 9)
35. Dx ⎜ ⎟=
⎝ 4 x 2 – 3x + 9 ⎠ (4 x 2 – 3x + 9)2
(4 x 2 – 3x + 9)(0) – (8 x – 3) 8x − 3
= =–
(4 x – 3 x + 9)
2 2
(4 x – 3x + 9)2
2

−8 x + 3
=
(4 x 2 – 3x + 9)2

⎛ 4 ⎞ (2 x3 – 3 x) Dx (4) – (4) Dx (2 x3 – 3 x)
36. Dx ⎜ ⎟ =
⎝ 2 x3 – 3x ⎠ (2 x3 – 3 x)2
(2 x3 – 3 x)(0) – 4(6 x 2 – 3) –24 x 2 + 12
= =
(2 x3 – 3 x)2 (2 x3 – 3x) 2

⎛ x –1 ⎞ ( x + 1) Dx ( x –1) – ( x –1) Dx ( x + 1)
37. Dx ⎜ ⎟=
⎝ x +1⎠ ( x + 1)2
( x + 1)(1) – ( x –1)(1) 2
= =
( x + 1) 2
( x + 1)2

⎛ 2 x –1 ⎞ ( x –1) Dx (2 x –1) – (2 x –1) Dx ( x –1)
38. Dx ⎜ ⎟=
⎝ x –1 ⎠ ( x –1) 2
( x –1)(2) – (2 x –1)(1) 1
= =–
2
( x –1) ( x –1) 2

⎛ 2 x 2 – 1 ⎞ (3 x + 5) Dx (2 x 2 –1) – (2 x 2 –1) Dx (3 x + 5)
39. Dx ⎜ ⎟ =
⎜ 3x + 5 ⎟ (3 x + 5)2
⎝ ⎠
(3 x + 5)(4 x) – (2 x 2 – 1)(3)
=
(3x + 5) 2
6 x 2 + 20 x + 3
=
(3x + 5)2

⎛ 5 x – 4 ⎞ (3 x 2 + 1) Dx (5 x – 4) – (5 x – 4) Dx (3x 2 + 1)
40. Dx ⎜ ⎟=
⎝ 3x2 + 1 ⎠ (3 x 2 + 1) 2
(3 x 2 + 1)(5) – (5 x – 4)(6 x)
=
(3x 2 + 1)2
−15 x 2 + 24 x + 5
=
(3x 2 + 1)2

⎛ 2 x 2 – 3 x + 1 ⎞ (2 x + 1) Dx (2 x 2 – 3x + 1) – (2 x 2 – 3x + 1) Dx (2 x + 1)
41. Dx ⎜ ⎟ =
⎜ 2x +1 ⎟ (2 x + 1)2
⎝ ⎠
(2 x + 1)(4 x – 3) – (2 x 2 – 3 x + 1)(2)
=
(2 x + 1)2
4 x2 + 4 x – 5
=
(2 x + 1) 2


⎛ 5 x 2 + 2 x – 6 ⎞ (3 x – 1) Dx (5 x 2 + 2 x – 6) – (5 x 2 + 2 x – 6) Dx (3 x – 1)
42. Dx ⎜ ⎟=
⎜ 3x – 1 ⎟ (3 x – 1)2
⎝ ⎠
(3 x – 1)(10 x + 2) – (5 x 2 + 2 x – 6)(3)
=
(3x – 1)2
15 x 2 – 10 x + 16
=
(3x – 1)2

⎛ x 2 – x + 1 ⎞ ( x 2 + 1) Dx ( x 2 – x + 1) – ( x 2 – x + 1) Dx ( x 2 + 1)
43. Dx ⎜ ⎟ =
⎜ x2 + 1 ⎟ ( x 2 + 1)2
⎝ ⎠
( x 2 + 1)(2 x – 1) – ( x 2 – x + 1)(2 x)
=
( x 2 + 1)2
x2 – 1
=
( x 2 + 1)2

⎛ x 2 – 2 x + 5 ⎞ ( x 2 + 2 x – 3) Dx ( x 2 – 2 x + 5) – ( x 2 – 2 x + 5) Dx ( x 2 + 2 x – 3)
44. Dx ⎜ ⎟=
⎜ x2 + 2 x – 3 ⎟ ( x 2 + 2 x – 3) 2
⎝ ⎠
( x 2 + 2 x – 3)(2 x – 2) – ( x 2 – 2 x + 5)(2 x + 2)
=
( x 2 + 2 x – 3) 2
4 x 2 – 16 x – 4
=
( x 2 + 2 x – 3) 2

45. a. ( f ⋅ g )′(0) = f (0) g ′(0) + g (0) f ′(0)
= 4(5) + (–3)(–1) = 23

b. ( f + g )′(0) = f ′(0) + g ′(0) = –1 + 5 = 4

g (0) f ′(0) – f (0) g ′(0)
c. ( f g )′(0) =
g 2 (0)
–3(–1) – 4(5) 17
= =–
2 9
(–3)

46. a. ( f – g )′(3) = f ′(3) – g ′(3) = 2 – (–10) = 12

b. ( f ⋅ g )′(3) = f (3) g ′(3) + g (3) f ′(3) = 7(–10) + 6(2) = –58

f (3) g ′(3) – g (3) f ′(3) 7(–10) – 6(2) 82
c. ( g f )′(3) = = =–
2 2 49
f (3) (7)

47. Dx [ f ( x )]2 = Dx [ f ( x ) f ( x)]
= f ( x) Dx [ f ( x)] + f ( x) Dx [ f ( x)]
= 2 ⋅ f ( x ) ⋅ Dx f ( x )

48. Dx [ f ( x) g ( x)h( x)] = f ( x) Dx [ g ( x)h( x)] + g ( x)h( x) Dx f ( x)
= f ( x)[ g ( x) Dx h( x) + h( x) Dx g ( x)] + g ( x)h( x) Dx f ( x)
= f ( x) g ( x) Dx h( x ) + f ( x)h( x) Dx g ( x) + g ( x)h( x) Dx f ( x)


49. Dx ( x 2 – 2 x + 2) = 2 x – 2 54. Proof #1:
At x = 1: m tan = 2 (1) – 2 = 0 Dx [ f ( x) − g ( x) ] = Dx [ f ( x) + (−1) g ( x) ]
Tangent line: y = 1
= Dx [ f ( x) ] + Dx [ (−1) g ( x) ]
⎛ 1 ⎞ ( x + 4) Dx (1) – (1) Dx ( x + 4)
2 2 = Dx f ( x) − Dx g ( x)
50. Dx ⎜ ⎟=
⎝ x2 + 4 ⎠ ( x 2 + 4)2
Proof #2:
( x 2 + 4)(0) – (2 x) 2x
= =– Let F ( x) = f ( x) − g ( x) . Then
( x 2 + 4)2 ( x 2 + 4) 2

At x = 1: mtan = −
2(1)
=–
2
F '( x) = lim
[ f ( x + h) − g ( x + h) ] − [ f ( x ) − g ( x ) ]
(1 + 4) 2 2 25
h →0 h
1 2
Tangent line: y – = – ( x –1) ⎡ f ( x + h) − f ( x ) g ( x + h ) − g ( x ) ⎤
5 25 = lim ⎢ − ⎥
h →0 ⎣ h h ⎦
2 7 = f '( x) − g '( x)
y = – x+
25 25

51. Dx ( x3 – x 2 ) = 3 x 2 – 2 x 55. a. Dt (–16t 2 + 40t + 100) = –32t + 40
The tangent line is horizontal when m tan = 0: v = –32(2) + 40 = –24 ft/s
mtan = 3x 2 – 2 x = 0
b. v = –32t + 40 = 0
x(3 x − 2) = 0
t=5 s
2 4
x = 0 and x =
3
56. Dt (4.5t 2 + 2t ) = 9t + 2
⎛2 4 ⎞
(0, 0) and ⎜ , – ⎟ 9t + 2 = 30
⎝ 3 27 ⎠ 28
t= s
9
⎛1 ⎞
52. Dx ⎜ x3 + x 2 – x ⎟ = x 2 + 2 x –1
⎝ 3 ⎠ 57. mtan = Dx (4 x – x 2 ) = 4 – 2 x
mtan = x + 2 x –1 = 1
2
The line through (2,5) and (x 0 , y0 ) has slope
x2 + 2 x – 2 = 0 y0 − 5
.
–2 ± 4 – 4(1)(–2) –2 ± 12 x0 − 2
x= =
2 2 4 x0 – x0 2 – 5
4 – 2 x0 =
= –1 – 3, –1 + 3 x0 – 2
x = –1 ± 3 –2 x02 + 8 x0 – 8 = – x0 2 + 4 x0 – 5
⎛ 5 ⎞ ⎛ 5 ⎞
⎜ −1 + 3, − 3 ⎟ , ⎜ −1 − 3, + 3 ⎟ x0 2 – 4 x0 + 3 = 0
⎝ 3 ⎠ ⎝ 3 ⎠
( x0 – 3)( x0 –1) = 0
53. y = 100 / x5 = 100 x −5 x 0 = 1, x0 = 3

y ' = −500 x −6 At x 0 = 1: y0 = 4(1) – (1)2 = 3
mtan = 4 – 2(1) = 2
Set y ' equal to −1 , the negative reciprocal of Tangent line: y – 3 = 2(x – 1); y = 2x + 1
the slope of the line y = x . Solving for x gives At x0 = 3 : y0 = 4(3) – (3)2 = 3
x = ±5001/ 6 ≈ ±2.817 mtan = 4 – 2(3) = –2
y = ±100(500)−5 / 6 ≈ ±0.563 Tangent line: y – 3 = –2(x – 3); y = –2x + 9

The points are (2.817,0.563) and
(−2.817,−0.563) .


4 3
58. Dx ( x 2 ) = 2 x 61. The watermelon has volume πr ; the volume
3
The line through (4, 15) and ( x0 , y0 ) has slope
of the rind is
y0 − 15 3
. If (x 0 , y0 ) is on the curve y = x 2 , then 4 3 4 ⎛ r ⎞ 271 3
x0 − 4 V= πr – π ⎜ r – ⎟ = πr .
3 3 ⎝ 10 ⎠ 750
x02 –15
mtan = 2 x0 = . At the end of the fifth week r = 10, so
x0 – 4
271 2 271 542π
2 x0 2 – 8 x0 = x02 –15 DrV = πr = π(10)2 = ≈ 340 cm3
250 250 5
x0 2 – 8 x0 + 15 = 0 per cm of radius growth. Since the radius is
( x0 – 3)( x0 – 5) = 0 growing 2 cm per week, the volume of the rind is
542π
At x0 = 3 : y0 = (3)2 = 9 growing at the rate of (2) ≈ 681 cm3 per
5
She should shut off the engines at (3, 9). (At week.
x 0 = 5 she would not go to (4, 15) since she is
moving left to right.)
2.4 Concepts Review
59. Dx (7 – x ) = –2 x
2
sin( x + h) – sin( x)
The line through (4, 0) and ( x0 , y0 ) has 1.
h
y0 − 0
slope . If the fly is at ( x0 , y0 ) when the
x0 − 4 2. 0; 1
2
7 – x0 – 0 3. cos x; –sin x
spider sees it, then mtan = –2 x0 = .
x0 – 4
–2 x02 + 8 x0 = 7 – x02 π 1 3 1⎛ π⎞
4. cos = ;y– = ⎜x– ⎟
3 2 2 2⎝ 3⎠
x 02 – 8x 0 + 7 = 0
( x0 – 7)( x0 –1) = 0
At x0 = 1: y0 = 6 Problem Set 2.4
d = (4 – 1)2 + (0 – 6) 2 = 9 + 36 = 45 = 3 5 1. Dx(2 sin x + 3 cos x) = 2 Dx(sin x) + 3 Dx(cos x)
≈ 6. 7 = 2 cos x – 3 sin x
They are 6.7 units apart when they see each
other. 2. Dx (sin 2 x) = sin x Dx (sin x ) + sin x Dx (sin x)
= sin x cos x + sin x cos x = 2 sin x cos x = sin 2x
⎛ 1⎞ 1
60. P(a, b) is ⎜ a, ⎟ . Dx y = – so the slope of
⎝ a⎠ x2 3. Dx (sin 2 x + cos 2 x) = Dx (1) = 0
1
the tangent line at P is – . The tangent line is
a2 4. Dx (1 – cos 2 x) = Dx (sin 2 x)
1 1 1 = sin x Dx (sin x) + sin x Dx (sin x)
y– =– ( x – a ) or y = – ( x – 2a ) which
2
a a a2 = sin x cos x + sin x cos x
has x-intercept (2a, 0). = 2 sin x cos x = sin 2x
1 1
d (O, P ) = a 2 + , d ( P, A) = (a – 2a )2 + ⎛ 1 ⎞
a 2
a2 5. Dx (sec x) = Dx ⎜ ⎟
⎝ cos x ⎠
1
= a2 + = d (O, P ) so AOP is an isosceles cos x Dx (1) – (1) Dx (cos x )
a2 =
cos 2 x
triangle. The height of AOP is a while the base,
sin x 1 sin x
1
OA has length 2a, so the area is (2 a)(a) = a2 . = = ⋅ = sec x tan x
2 cos x cos x
2 cos x


⎛ 1 ⎞ ⎛ sin x + cos x ⎞
6. Dx (csc x) = Dx ⎜ ⎟ 10. Dx ⎜ ⎟
⎝ sin x ⎠ ⎝ tan x ⎠
sin x Dx (1) − (1) Dx (sin x ) tan x Dx (sin x + cos x) − (sin x + cos x) Dx (tan x )
= =
sin 2 x tan 2 x
– cos x –1 cos x tan x(cos x – sin x) – sec2 x(sin x + cos x)
= = ⋅ = – csc x cot x =
2
sin x sin x sin x tan 2 x
⎛ sin 2 x sin x 1 ⎞ ⎛ sin 2 x ⎞
⎛ sin x ⎞ = ⎜ sin x – – – ⎟ ÷⎜ ⎟
7. Dx (tan x) = Dx ⎜ ⎟ ⎝ cos x cos x cos x ⎠ ⎝ cos 2 x ⎠
2

⎝ cos x ⎠
cos x Dx (sin x) − sin x Dx (cos x) ⎛ sin 2 x sin x 1 ⎞⎛ cos 2 x ⎞
= = ⎜ sin x − − − ⎟⎜ ⎟
cos 2 x ⎝ cos x cos x cos x ⎠⎝ sin 2 x ⎠
2

cos 2 x + sin 2 x 1 cos 2 x 1 cos x
= = = sec2 x = − cos x − −
cos2 x cos 2 x sin x sin x sin 2 x

⎛ cos x ⎞ 11. Dx ( sin x cos x ) = sin xDx [ cos x ] + cos xDx [sin x ]
8. Dx (cot x) = Dx ⎜ ⎟
⎝ sin x ⎠ = sin x ( − sin x ) + cos x ( cos x ) = cos 2 x − sin 2 x
sin x Dx (cos x) − cos x Dx (sin x)
=
sin 2 x 12. Dx ( sin x tan x ) = sin xDx [ tan x ] + tan xDx [sin x ]
− sin x – cos x –(sin x + cos x)
( )
2 2 2 2
= = = sin x sec2 x + tan x ( cos x )
2 2
sin x sin x
⎛ 1 ⎞ sin x
=–
1
= – csc2 x
= sin x ⎜ ⎟+ ( cos x )
2 ⎝ cos 2 x ⎠ cos x
sin x
= tan x sec x + sin x
⎛ sin x + cos x ⎞
9. Dx ⎜ ⎟ ⎛ sin x ⎞ xDx ( sin x ) − sin xDx ( x )
⎝ cos x ⎠ 13. Dx ⎜ ⎟=
cos x Dx (sin x + cos x) − (sin x + cos x) Dx (cos x) ⎝ x ⎠ x2
= x cos x − sin x
cos 2 x =
x2
cos x(cos x – sin x) – (– sin 2 x – sin x cos x)
=
cos 2 x ⎛ 1 − cos x ⎞ xDx (1 − cos x ) − (1 − cos x ) Dx ( x )
cos 2 x + sin 2 x
14. Dx ⎜ ⎟=
= =
1
= sec2 x ⎝ x ⎠ x2
cos2 x cos 2 x x sin x + cos x − 1
=
x2

15. Dx ( x 2 cos x) = x 2 Dx (cos x) + cos x Dx ( x 2 )
= − x 2 sin x + 2 x cos x

⎛ x cos x + sin x ⎞
16. Dx ⎜ ⎟
⎝ x2 + 1 ⎠
( x 2 + 1) Dx ( x cos x + sin x) − ( x cos x + sin x) Dx ( x 2 + 1)
=
( x 2 + 1) 2
( x 2 + 1)(– x sin x + cos x + cos x) – 2 x( x cos x + sin x)
=
( x 2 + 1)2
– x3 sin x – 3 x sin x + 2 cos x
=
( x 2 + 1) 2


17. y = tan 2 x = (tan x)(tan x) b. Dt(20 sin t) = 20 cos t
π π
Dx y = (tan x)(sec 2 x ) + (tan x)(sec 2 x) At t = : rate = 20 cos = 10 3 ≈ 17. 32 ft/s
6 6
= 2 tan x sec 2 x
c. The fastest rate 20 cos t can obtain is
20 ft/s.
18. y = sec x = (sec x)(sec x)
3 2

Dx y = (sec 2 x) sec x tan x + (sec x) Dx (sec2 x) 25. y = tan x
= sec3 x tan x + sec x(sec x ⋅ sec x tan x y ' = sec2 x
+ sec x ⋅ sec x tan x) When y = 0 , y = tan 0 = 0 and y ' = sec 2 0 = 1 .
= sec3 x tan x + 2sec3 x tan x The tangent line at x = 0 is y = x .
= 3sec2 x tan x
26. y = tan 2 x = (tan x)(tan x)
19. Dx(cos x) = –sin x y ' = (tan x)(sec 2 x) + (tan x)(sec2 x)
At x = 1: mtan = – sin1 ≈ –0.8415
= 2 tan x sec 2 x
y = cos 1 ≈ 0.5403
Now, sec2 x is never 0, but tan x = 0 at
Tangent line: y – 0.5403 = –0.8415(x – 1)
x = kπ where k is an integer.
20. Dx (cot x) = – csc2 x 27. y = 9sin x cos x
π
At x = : mtan = –2; y ' = 9 [sin x(− sin x) + cos x(cos x) ]
4
y=1 = 9 ⎡sin 2 x − cos 2 x ⎤
⎣ ⎦
⎛ π⎞
Tangent line: y –1 = –2 ⎜ x – ⎟ = 9 [ − cos 2 x ]
⎝ 4⎠
The tangent line is horizontal when y ' = 0 or, in
21. Dx sin 2 x = Dx (2sin x cos x) this case, where cos 2 x = 0 . This occurs when
= 2 ⎡sin x Dx cos x + cos x Dx sin x ⎤ π π
⎣ ⎦ x= +k where k is an integer.
4 2
= −2sin x + 2 cos x
2 2

28. f ( x) = x − sin x
22. Dx cos 2 x = Dx (2 cos x − 1) = 2 Dx cos x − Dx 1
2 2
f '( x) = 1 − cos x
= −2sin x cos x f '( x) = 0 when cos x = 1 ; i.e. when x = 2kπ
where k is an integer.
23. Dt (30sin 2t ) = 30 Dt (2sin t cos t )
f '( x) = 2 when x = (2k + 1)π where k is an
(
= 30 −2sin 2 t + 2 cos 2 t ) integer.
= 60 cos 2t
29. The curves intersect when 2 sin x = 2 cos x,
30sin 2t = 15
sin x = cos x at x = π for 0 < x < π .
1 4 2
sin 2t =
2 π
Dx ( 2 sin x) = 2 cos x ; 2 cos = 1
π π 4
2t = → t=
6 12 π
Dx ( 2 cos x) = – 2 sin x ; − 2 sin = −1
π ⎛ π ⎞ 4
At t = ; 60 cos ⎜ 2 ⋅ ⎟ = 30 3 ft/sec 1(–1) = –1 so the curves intersect at right angles.
12 ⎝ 12 ⎠
The seat is moving to the left at the rate of 30 3 30. v = Dt (3sin 2t ) = 6 cos 2t
ft/s. At t = 0: v = 6 cm/s
π
24. The coordinates of the seat at time t are t = : v = −6 cm/s
2
(20 cos t, 20 sin t).
t = π : v = 6 cm/s
⎛ π π⎞
a. ⎜ 20 cos , 20sin ⎟ = (10 3, 10)
⎝ 6 6⎠
≈ (17.32, 10)


sin( x + h) 2 – sin x 2
31. Dx (sin x 2 ) = lim
h→0 h
sin( x 2 + 2 xh + h 2 ) – sin x 2
= lim
h→0 h
sin x 2 cos(2 xh + h 2 ) + cos x 2 sin(2 xh + h 2 ) – sin x 2 sin x 2 [cos(2 xh + h 2 ) – 1] + cos x 2 sin(2 xh + h 2 )
= lim = lim
h →0 h h→0 h
⎡ cos(2 xh + h 2 ) – 1 sin(2 xh + h 2 ) ⎤
= lim(2 x + h) ⎢sin x 2 + cos x 2 ⎥ = 2 x(sin x 2 ⋅ 0 + cos x 2 ⋅1) = 2 x cos x 2
h →0 ⎢
⎣ 2 xh + h 2 2 xh + h 2 ⎥ ⎦

sin(5( x + h)) – sin 5 x 34. f ( x ) = cos3 x − 1.25cos 2 x + 0.225
32. Dx (sin 5 x) = lim
h →0 h
sin(5 x + 5h) – sin 5 x
= lim
h →0 h
sin 5 x cos 5h + cos 5 x sin 5h – sin 5 x
= lim
h →0 h
⎡ cos 5h – 1 sin 5h ⎤
= lim ⎢sin 5 x + cos 5 x
h→0 ⎣ h h ⎥ ⎦
⎡ cos 5h – 1 sin 5h ⎤
= lim ⎢5sin 5 x + 5cos 5 x
h→0 ⎣ 5h 5h ⎥ ⎦
= 0 + 5cos 5 x ⋅1 = 5cos 5 x x0 ≈ 1.95
f ′ (x 0 ) ≈ –1. 24
33. f(x) = x sin x

a. 2.5 Concepts Review

1. Dt u; f ′( g (t )) g ′(t )

2. Dv w; G ′( H ( s )) H ′( s )

3. ( f ( x)) 2 ;( f ( x)) 2
b. f(x) = 0 has 6 solutions on [π , 6π ]
f ′ (x) = 0 has 5 solutions on [π , 6π ]
4. 2 x cos( x );6(2 x + 1)
2 2

c. f(x) = x sin x is a counterexample.
Consider the interval [ 0, π ] . Problem Set 2.5
f ( −π ) = f (π ) = 0 and f ( x ) = 0 has
1. y = u15 and u = 1 + x
exactly two solutions in the interval (at 0 and
Dx y = Du y ⋅ Dx u
π ). However, f ' ( x ) = 0 has two solutions
in the interval, not 1 as the conjecture = (15u14 )(1)
indicates it should have. = 15(1 + x )14

d. The maximum value of f ( x) – f ′( x) on
2. y = u5 and u = 7 + x
[π , 6π ] is about 24.93. Dx y = Du y ⋅ Dx u
= (5u 4 )(1)
= 5(7 + x)4

3. y = u5 and u = 3 – 2x
= (5u 4 )(–2) = –10(3 – 2 x) 4


4. y = u7 and u = 4 + 2 x 2 10. y = cos u and u = 3 x 2 – 2 x
Dx y = Du y ⋅ Dx u Dx y = Du y ⋅ Dx u
= (7u 6 )(4 x) = 28 x(4 + 2 x 2 )6 = (–sin u)(6x – 2)
= –(6 x – 2) sin(3x 2 – 2 x)
5. y = u11 and u = x3 – 2 x 2 + 3 x + 1
Dx y = Du y ⋅ Dx u 11. y = u 3 and u = cos x
= (11u10 )(3x 2 – 4 x + 3)
= (3u 2 )(– sin x)
= 11(3 x 2 – 4 x + 3)( x3 – 2 x 2 + 3x + 1)10
= –3sin x cos 2 x
6. y = u –7 and u = x 2 – x + 1
12. y = u 4 , u = sin v, and v = 3 x 2
Dx y = Du y ⋅ Dv u ⋅ Dx v
= (–7u –8 )(2 x – 1)
= (4u 3 )(cos v )(6 x)
= –7(2 x – 1)( x 2 – x + 1) –8
= 24 x sin 3 (3 x 2 ) cos(3 x 2 )
7. y = u –5 and u = x + 3
x +1
Dx y = Du y ⋅ Dx u 13. y = u 3 and u =
x –1
5 Dx y = Du y ⋅ Dx u
= (–5u –6 )(1) = –5( x + 3) –6 = –
( x + 3)6 ( x –1) Dx ( x + 1) – ( x + 1) Dx ( x –1)
= (3u 2 )
( x –1) 2
8. y = u and u = 3x + x – 3
–9 2
2⎛
⎛ x +1⎞ –2 ⎞ 6( x + 1) 2
Dx y = Du y ⋅ Dx u = 3⎜ ⎟ ⎜ ⎟=−
⎝ x –1⎠ ⎜ ( x – 1)2 ⎟ ( x – 1)4
= (–9u –10 )(6 x + 1) ⎝ ⎠

= –9(6 x + 1)(3 x 2 + x – 3) –10 x−2
14. y = u −3 and u =
9(6 x + 1) x−π
=–
(3 x 2 + x – 3)10 Dx y = Du y ⋅ Dx u
( x − π) Dx ( x − 2) − ( x − 2) Dx ( x − π)
= (−3u −4 ) ⋅
9. y = sin u and u = x + x 2
( x − π) 2
Dx y = Du y ⋅ Dx u −4
⎛ x−2⎞ (2 − π) ( x − π)2
= (cos u)(2x + 1) = −3 ⎜ ⎟ = −3 (2 − π)
⎝ x−π⎠ ( x − π) 2 ( x − 2)4
= (2 x + 1) cos( x + x)
2

3x 2
15. y = cos u and u =
x+2
( x + 2) Dx (3 x 2 ) – (3x 2 ) Dx ( x + 2)
Dx y = Du y ⋅ Dx u = (– sin u )
( x + 2) 2
⎛ 3x 2 ⎞ ( x + 2)(6 x) – (3x 2 )(1) 3 x 2 + 12 x ⎛ 3x 2 ⎞
= – sin ⎜ ⎟ =– sin ⎜ ⎟
⎜ x+2⎟ ⎜ ⎟
⎝ ⎠ ( x + 2)2 ( x + 2)2 ⎝ x+2⎠

x2
16. y = u 3 , u = cos v, and v =
1– x
(1 – x) Dx ( x 2 ) – ( x 2 ) Dx (1 − x)
Dx y = Du y ⋅ Dv u ⋅ Dx v = (3u 2 )(− sin v)
(1 – x) 2
⎛ x 2 ⎞ ⎛ x 2 ⎞ (1 – x)(2 x) – ( x 2 )(–1) –3(2 x – x 2 ) ⎛ x2 ⎞ ⎛ x2 ⎞
= –3cos 2 ⎜ ⎟ sin ⎜ ⎟ = cos 2 ⎜ ⎟ sin ⎜ ⎟
⎜1– x ⎟ ⎜1– x ⎟ (1 – x)2 (1 – x)2 ⎜1– x ⎟ ⎜1– x ⎟
⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠


17. Dx [(3 x – 2)2 (3 – x 2 ) 2 ] = (3 x – 2)2 Dx (3 – x 2 )2 + (3 – x 2 ) 2 Dx (3 x – 2)2
= (3 x – 2)2 (2)(3 – x 2 )(–2 x) + (3 – x 2 ) 2 (2)(3 x – 2)(3)
= 2(3 x − 2)(3 − x 2 )[(3 x − 2)(−2 x) + (3 − x 2 )(3)] = 2(3 x − 2)(3 − x 2 )(9 + 4 x − 9 x 2 )

18. Dx [(2 – 3x 2 )4 ( x 7 + 3)3 ] = (2 – 3 x 2 )4 Dx ( x 7 + 3)3 + ( x 7 + 3)3 Dx (2 – 3x 2 ) 4
= (2 – 3 x 2 )4 (3)( x 7 + 3) 2 (7 x 6 ) + ( x 7 + 3)3 (4)(2 – 3 x 2 )3 (–6 x) = 3x (3 x 2 – 2)3 ( x 7 + 3) 2 (29 x 7 – 14 x5 + 24)

⎡ ( x + 1)2 ⎤ (3x – 4) Dx ( x + 1)2 – ( x + 1)2 Dx (3x – 4) (3 x – 4)(2)( x + 1)(1) – ( x + 1)2 (3) 3 x 2 – 8 x – 11
19. Dx ⎢ ⎥= = =
⎢ 3x – 4 ⎥
⎣ ⎦ (3 x – 4)2 (3x – 4) 2 (3x – 4) 2
( x + 1)(3 x − 11)
=
(3x − 4)2

⎡ 2 x – 3 ⎤ ( x 2 + 4) 2 Dx (2 x – 3) – (2 x – 3) Dx ( x 2 + 4)2
20. Dx ⎢ ⎥=
⎢ ( x 2 + 4) 2 ⎥
⎣ ⎦ ( x 2 + 4) 4
( x 2 + 4) 2 (2) – (2 x – 3)(2)( x 2 + 4)(2 x) −6 x 2 + 12 x + 8
= =
( x 2 + 4) 4 ( x 2 + 4)3

( ′
)( ) ( )
21. y ′ = 2 x 2 + 4 x 2 + 4 = 2 x 2 + 4 (2 x ) = 4 x x 2 + 4 ( )
22. y ′ = 2(x + sin x )(x + sin x )′ = 2(x + sin x )(1 + cos x )

3 2
⎛ 3t – 2 ⎞ ⎛ 3t – 2 ⎞ (t + 5) Dt (3t – 2) – (3t – 2) Dt (t + 5)
23. Dt ⎜ `⎟ = 3 ⎜ ⎟
⎝ t +5 ⎠ ⎝ t +5 ⎠ (t + 5)2
2
⎛ 3t – 2 ⎞ (t + 5)(3) – (3t – 2)(1) 51(3t – 2)2
= 3⎜ ⎟ =
⎝ t +5 ⎠ (t + 5)2 (t + 5) 4

⎛ s 2 – 9 ⎞ ( s + 4) Ds ( s 2 – 9) – ( s 2 – 9) Ds ( s + 4) ( s + 4)(2s ) – ( s 2 – 9)(1) s 2 + 8s + 9
24. Ds ⎜ ⎟= = =
⎜ s+4 ⎟ ( s + 4)2 ( s + 4) 2 ( s + 4)2
⎝ ⎠

d d
(t + 5) (3t − 2)3 − (3t − 2)3 (t + 5)
d ⎛ (3t − 2)3 ⎞ dt dt (t + 5)(3)(3t – 2)2 (3) – (3t – 2)3 (1)
25. ⎜ ⎟= =
dt ⎜ t + 5 ⎟
⎝ ⎠ (t + 5) 2 (t + 5)2
(6t + 47)(3t – 2)2
=
(t + 5) 2

d
26. (sin 3 θ ) = 3sin 2 θ cos θ
dθ

d d
3 2 2 (cos 2 x) (sin x) − (sin x) (cos 2 x)
dy d ⎛ sin x ⎞ ⎛ sin x ⎞ d sin x ⎛ sin x ⎞ dx dx
27. = ⎜ ⎟ = 3⎜ ⎟ ⋅ = 3⎜ ⎟ ⋅
dx dx ⎝ cos 2 x ⎠ ⎝ cos 2 x ⎠ dx cos 2 x ⎝ cos 2 x ⎠ cos 2 2 x
2
⎛ sin x ⎞ cos x cos 2 x + 2sin x sin 2 x 3sin x cos x cos 2 x + 6sin x sin 2 x
2 3
= 3⎜ ⎟ =
⎝ cos 2 x ⎠ cos 2 2 x cos 4 2 x
3(sin 2 x)(cos x cos 2 x + 2sin x sin 2 x)
=
cos 4 2 x


dy d d d
28. = [sin t tan(t 2 + 1)] = sin t ⋅ [tan(t 2 + 1)] + tan(t 2 + 1) ⋅ (sin t )
dt dt dt dt
= (sin t )[sec 2 (t 2 + 1)](2t ) + tan(t 2 + 1) cos t = 2t sin t sec2 (t 2 + 1) + cos t tan(t 2 + 1)

2 2
⎛ x 2 + 1 ⎞ ( x + 2) Dx ( x 2 + 1) – ( x 2 + 1) Dx ( x + 2) ⎛ x 2 + 1 ⎞ 2 x 2 + 4 x – x 2 – 1 3( x 2 + 1)2 ( x 2 + 4 x – 1)
29. f ′( x) = 3 ⎜ ⎟ = 3⎜ ⎟ =
⎜ x+2 ⎟ ( x + 2) 2 ⎜ x+2 ⎟ ( x + 2) 2 ( x + 2)4
⎝ ⎠ ⎝ ⎠
f ′(3) = 9.6

30. G ′(t ) = (t 2 + 9)3 Dt (t 2 – 2)4 + (t 2 – 2) 4 Dt (t 2 + 9)3 = (t 2 + 9)3 (4)(t 2 – 2)3 (2t ) + (t 2 – 2) 4 (3)(t 2 + 9)2 (2t )
= 2t (7t 2 + 30)(t 2 + 9)2 (t 2 – 2)3
G ′(1) = –7400

31. F ′(t ) = [cos(t 2 + 3t + 1)](2t + 3) = (2t + 3) cos(t 2 + 3t + 1) ; F ′(1) = 5cos 5 ≈ 1.4183

32. g ′( s ) = (cos πs ) Ds (sin 2 πs ) + (sin 2 πs ) Ds (cos πs ) = (cos πs )(2sin πs )(cos πs )(π) + (sin 2 πs )(– sin πs )(π)
= π sin πs[2 cos 2 πs – sin 2 πs ]
⎛1⎞
g ′ ⎜ ⎟ = –π
⎝2⎠

33. Dx [sin 4 ( x 2 + 3x)] = 4sin 3 ( x 2 + 3x) Dx sin( x 2 + 3x) = 4sin 3 ( x 2 + 3 x) cos( x 2 + 3 x) Dx ( x 2 + 3 x)
= 4sin 3 ( x 2 + 3 x) cos( x 2 + 3x)(2 x + 3) = 4(2 x + 3) sin 3 ( x 2 + 3x) cos( x 2 + 3 x)

34. Dt [cos5 (4t – 19)] = 5cos 4 (4t – 19) Dt cos(4t – 19) = 5cos 4 (4t – 19)[– sin(4t – 19)]Dt (4t – 19)
= –5cos 4 (4t – 19) sin(4t – 19)(4) = –20 cos (4t – 19) sin(4t – 19)
4

35. Dt [sin 3 (cos t )] = 3sin 2 (cos t ) Dt sin(cos t ) = 3sin 2 (cos t ) cos(cos t ) Dt (cos t )
= 3sin 2 (cos t ) cos(cos t )(– sin t ) = –3sin t sin (cos t ) cos(cos t )
2

⎡ ⎛ u + 1 ⎞⎤ 3 ⎛ u +1⎞ ⎛ u +1⎞ 3 ⎛ u +1⎞ ⎡ ⎛ u + 1 ⎞⎤ ⎛ u + 1 ⎞
36 . Du ⎢cos4 ⎜ ⎟ ⎥ = 4 cos ⎜ ⎟ Du cos ⎜ ⎟ = 4 cos ⎜ ⎟ ⎢ – sin ⎜ ⎟ ⎥ Du ⎜ ⎟
⎣ ⎝ u –1 ⎠ ⎦ ⎝ u –1 ⎠ ⎝ u –1 ⎠ ⎝ u –1 ⎠ ⎣ ⎝ u –1 ⎠ ⎦ ⎝ u –1 ⎠
⎛ u + 1 ⎞ ⎛ u + 1 ⎞ (u –1) Du (u + 1) – (u + 1) Du (u –1) 8 ⎛ u +1⎞ ⎛ u +1⎞
= –4 cos3 ⎜ ⎟ sin ⎜ ⎟ = cos3 ⎜ ⎟ sin ⎜ ⎟
⎝ u –1 ⎠ ⎝ u –1 ⎠ (u –1) 2
(u –1) 2 ⎝ u –1 ⎠ ⎝ u –1 ⎠

37. Dθ [cos 4 (sin θ 2 )] = 4 cos3 (sin θ 2 ) Dθ cos(sin θ 2 ) = 4 cos3 (sin θ 2 )[– sin(sin θ 2 )]Dθ (sin θ 2 )
= –4 cos3 (sin θ 2 ) sin(sin θ 2 )(cosθ 2 ) Dθ (θ 2 ) = –8θ cos3 (sin θ 2 ) sin(sin θ 2 )(cos θ 2 )

38. Dx [ x sin 2 (2 x)] = x Dx sin 2 (2 x) + sin 2 (2 x) Dx x = x[2sin(2 x) Dx sin(2 x)] + sin 2 (2 x)(1)
= x[2sin(2 x ) cos(2 x) Dx (2 x)] + sin 2 (2 x) = x[4sin(2 x) cos(2 x)] + sin 2 (2 x) = 2 x sin(4 x) + sin 2 (2 x)

39. Dx {sin[cos(sin 2 x)]} = cos[cos(sin 2 x)]Dx cos(sin 2 x) = cos[cos(sin 2 x)][– sin(sin 2 x)]Dx (sin 2 x)
= – cos[cos(sin 2 x)]sin(sin 2 x)(cos 2 x) Dx (2 x) = –2 cos[cos(sin 2 x)]sin(sin 2 x)(cos 2 x)

40. Dt {cos 2 [cos(cos t )]} = 2 cos[cos(cos t )]Dt cos[cos(cos t )] = 2 cos[cos(cos t )]{– sin[cos(cos t )]}Dt cos(cos t )
= –2 cos[cos(cos t )]sin[cos(cos t )][– sin(cos t )]Dt (cos t ) = 2 cos[cos(cos t )]sin[cos(cos t )]sin(cos t )(– sin t )
= –2sin t cos[cos(cos t )]sin[cos(cos t )]sin(cos t )


41. ( f + g )′(4) = f ′(4) + g ′(4) d d
53. F ( cos x ) = F ′ ( cos x ) ( cos x )
1 3 dx dx
≈ + ≈2
2 2 = − sin xF ′ ( cos x )

′ ′
42. (f − 2g ) ( 2) = f ′ ( 2) − ( 2g ) ( 2) 54.
d
cos ( F ( x ) ) = − sin ( F ( x ) ) F ( x )
d
dx dx
= f ′ ( 2) − 2g′ ( 2)
= − F ′ ( x ) sin ( F ( x ) )
= 1 − 2 ( 0) = 1
55. Dx ⎣ tan ( F ( 2 x ) ) ⎦ = sec 2 ( F ( 2 x ) ) Dx ⎡ F ( 2 x ) ⎤
⎡ ⎤ ⎣ ⎦
43. ( fg )′ (2 ) = ( fg ′ + gf ′)(2) = 2(0) + 1(1) = 1
= sec2 ( F ( 2 x ) ) × F ′ ( 2 x ) × Dx [ 2 x ]

44. ( f g )′(2) =
g (2) f ′(2) – f (2) g ′(2) = 2 F ′ ( 2 x ) sec2 ( F ( 2 x ) )
2
g (2)
d d
≈
(1)(1) – (3)(0)
=1 56. ⎡ g ( tan 2 x ) ⎤ = g ' ( tan 2 x ) ⋅ tan 2 x
⎣ ⎦
(1) 2 dx dx
(
= g ' ( tan 2 x ) sec2 2 x ⋅ 2 )
45. ( f g )′(6) = f ′( g (6)) g ′(6)
= 2 g ' ( tan 2 x ) sec2 2 x
= f ′(2) g ′(6) ≈ (1)(−1) = –1

46. ( g f )′(3) = g ′( f (3)) f ′(3) 57. Dx ⎡ F ( x ) sin 2 F ( x ) ⎤
⎣ ⎦
⎛3⎞
= g ′(4) f ′(3) ≈ ⎜ ⎟ (1) =
3 = F ( x ) × Dx ⎡sin F ( x ) ⎤ + sin 2 F ( x ) × Dx F ( x )
⎣
2
⎦
⎝ 2⎠ 2
= F ( x ) × 2sin F ( x ) × Dx ⎡sin F ( x ) ⎤
⎣ ⎦
47. D x F (2 x ) = F ′(2 x )D x (2 x ) = 2 F ′(2 x ) + F ′ ( x ) sin 2 F ( x )
= F ( x ) × 2sin F ( x ) × cos ( F ( x ) ) × Dx ⎡ F ( x ) ⎤
( ) (
Dx F x 2 +1 = F ′ x 2 +1 Dx x 2 +1 ) ( ) ⎣ ⎦

( ) + F ′ ( x ) sin 2 F ( x )
48.
= 2 xF ′ x 2 + 1
= 2 F ( x ) F ′ ( x ) sin F ( x ) cos F ( x )
[ ]
49. Dt (F (t ))−2 = −2(F (t ))−3 F ′(t ) + F ′ ( x ) sin 2 F ( x )

d ⎡ 1 ⎤ 58. Dx ⎣sec3 F ( x ) ⎦ = 3sec2 ⎡ F ( x ) ⎤ Dx ⎡sec F ( x ) ⎤
⎡ ⎤
⎥ = −2(F (z )) F ′(z )
−3 ⎣ ⎦ ⎣ ⎦
50. ⎢
dz ⎢ (F (z ))2 ⎥
⎣ ⎦ = 3sec2 ⎡ F ( x ) ⎤ sec F ( x ) tan F ( x ) Dx [ x ]
⎣ ⎦
= 3F ′ ( x ) sec3 F ( x ) tan F ( x )
⎢(
1 + F ( 2 z ) ) ⎤ = 2 (1 + F ( 2 z ) ) (1 + F ( 2 z ) )
d ⎡ 2 d
51.
dz ⎣ ⎥
⎦ dz
= 2 (1 + F ( 2 z ) ) ( 2 F ′ ( 2 z ) ) = 4 (1 + F ( 2 z ) ) F ′ ( 2 z ) 59. g ' ( x ) = − sin f ( x ) Dx f ( x ) = − f ′ ( x ) sin f ( x )
g ′ ( 0 ) = − f ′ ( 0 ) sin f ( 0 ) = −2sin1 ≈ −1.683
⎡ ⎤
( ( ))
−1 ⎤
d ⎢ 2
y +
1 ⎥ = 2 y + d ⎡ F y2
52.
dy ⎢ F y2 ( ) ⎥ dy ⎢
⎣
⎥
⎦ (1 + sec F ( 2 x ) ) dx x − x dx (1 + sec F ( 2 x ) )
d d
⎣ ⎦ 60. G ′ ( x ) =
( ) (1 + sec F ( 2 x ) )
2
2 yF ′ y 2

= 2 y − F ′ y2 ( ) dy y
d 2
= 2y −
(1 + sec F ( 2 x ) ) − 2 xF ′ ( 2 x ) sec F ( 2 x ) tan F ( 2 x )
( F ( y ))
2
2
=
(1 + sec F ( 2 x ) )
2

⎛ ⎞
⎜
= 2 y ⎜1 −
F ′ y2 ( ) ⎟
G′ ( 0) =
1 + sec F ( 0 ) − 0
=
1 + sec F ( 0 )
2 ⎟
( ( )) (1 + sec F ( 0 ) ) (1 + sec F ( 0 ) )
2 2
⎜ F y2 ⎟
⎝ ⎠
1 1
= = ≈ −0.713
1 + sec F ( 0 ) 1 + sec 2


61. F ′ ( x ) = − f ( x ) g ′ ( x ) sin g ( x ) + f ′ ( x ) cos g ( x ) c. Dt L = 1
Dt (16cos2 2t + 49sin 2 2t )
F ′ (1) = − f (1) g ′ (1) sin g (1) + f ′ (1) cos g (1) 2 16cos2 2t + 49sin 2 2t
32 cos 2t Dt (cos 2t ) + 98sin 2t Dt (sin 2t )
= −2 (1) sin 0 + −1cos 0 = −1 =
2 16 cos 2 2t + 49sin 2 2t
62. y = 1 + x sin 3 x; y ′ = 3x cos 3 x + sin 3 x –64 cos 2t sin 2t + 196sin 2t cos 2t
=
π π π 2 16 cos 2 2t + 49sin 2 2t
y ′ (π / 3) = 3 cos 3 + sin = −π + 0 = −π
3 3 3 −16sin 4t + 49sin 4t
y − 1 = −π x − π / 3 =
16 cos 2 2t + 49sin 2 2t
y = −π x − π / 3 + 1
33sin 4t
3−π =
The line crosses the x-axis at x = . 16 cos 2 2t + 49sin 2 2t
3
π 33
63. y = sin 2 x; y ′ = 2sin x cos x = sin 2 x = 1 At t = : rate = ≈ 5.8 ft/sec.
8 16 ⋅ 1 + 49 ⋅ 1
x = π / 4 + kπ , k = 0, ± 1, ± 2,... 2 2

(10 cos8π t ,10sin 8π t )
( ) ( ) ( ) ( )
3 2 2 69. a.
64. y ′ = x 2 + 1 2 x 4 + 1 x3 + 3 x 2 + 1 x x 4 + 1
Dt (10sin 8πt ) = 10 cos(8πt ) Dt (8πt )
( x + 1)( x + 1) + 3x ( x + 1) ( x + 1)
3 2 2 b.
= 2 x3 4 2 4 2
= 80π cos(8πt )
y ′ (1) = 2 ( 2 )( 2 ) + 3 (1)( 2 ) ( 2 )2 = 32 + 48 = 80
3 2
At t = 1: rate = 80π ≈ 251 cm/s
y − 32 = 80 x − 1, y = 80 x + 31 P is rising at the rate of 251 cm/s.

70. a. (cos 2t, sin 2t)
( ) ( 2 x ) = −4 x ( x 2 + 1)
−3 −3
65. y ′ = −2 x 2 + 1
−3
b. (0 – cos 2t ) 2 + ( y – sin 2t )2 = 52 , so
y ′ (1) = −4 (1)(1 + 1) = −1/ 2
y = sin 2t + 25 – cos 2 2t
1 1 1 1 3
y− = − x+ , y = − x+
4 2 2 2 4
c. Dt ⎛ sin 2t + 25 − cos 2 2t ⎞
⎜ ⎟
⎝ ⎠
66. y ′ = 3 ( 2 x + 1) ( 2 ) = 6 ( 2 x + 1)
2 2
1
= 2 cos 2t + ⋅ 4 cos 2t sin 2t
y ′ ( 0 ) = 6 (1) = 6
2
2 25 − cos 2 2t
y − 1 = 6 x − 0, y = 6 x + 1
⎛ sin 2t ⎞
The line crosses the x-axis at x = −1/ 6 . = 2 cos 2t ⎜ 1 + ⎟
⎜ ⎟
⎝ 25 – cos 2 2t ⎠
( ) ( 2 x ) = −4 x ( x 2 + 1)
−3 −3
67. y ′ = −2 x 2 + 1
71. 60 revolutions per minute is 120π radians per
y ′ (1) = −4 ( 2 )
−3
= −1/ 2 minute or 2π radians per second.
1 1 1 1 3 (cos 2π t ,sin 2π t )
y− = − x+ , y = − x+ a.
4 2 2 2 4
Set y = 0 and solve for x. The line crosses the
b. (0 – cos 2πt ) 2 + ( y – sin 2πt )2 = 52 , so
x-axis at x = 3 / 2 .
y = sin 2πt + 25 – cos 2 2πt
2 2 2 2
⎛x⎞ ⎛ y⎞ ⎛ 4 cos 2t ⎞ ⎛ 7 sin 2t ⎞
68. a. ⎜ ⎟ +⎜ ⎟ = ⎜ ⎟ +⎜ ⎟
⎝4⎠ ⎝7⎠ ⎝ 4 ⎠ ⎝ 7 ⎠ c. Dt ⎛ sin 2πt + 25 − cos 2 2πt ⎞
⎜ ⎟
⎝ ⎠
= cos 2 2t + sin 2 2t = 1
= 2π cos 2πt
1
b. L = ( x – 0)2 + ( y – 0) 2 = x 2 + y 2 + ⋅ 4π cos 2πt sin 2πt
2 25 − cos 2 2πt
= (4 cos 2t )2 + (7 sin 2t )2
⎛ sin 2πt ⎞
= 16 cos 2 2t + 49sin 2 2t = 2π cos 2πt ⎜ 1 + ⎟
⎜ ⎟
⎝ 25 – cos 2 2πt ⎠


72. The minute hand makes 1 revolution every hour,
ds 22π sin 11πt
so at t minutes after the hour, it makes an angle 74. From Problem 73, = 360
.
πt dt 15 100 – 96 cos 11πt
of radians with the vertical. By the Law of 360
30 Using a computer algebra system or graphing
Cosines, the length of the elastic string is ds ds
utility to view for 0 ≤ t ≤ 60 , is largest
πt dt dt
s = 102 + 102 – 2(10)(10) cos
30 when t ≈ 7.5. Thus, the distance between the tips
πt of the hands is increasing most rapidly at about
= 10 2 – 2 cos 12:08.
30
75. sin x0 = sin 2 x0
ds 1 π πt
= 10 ⋅ ⋅
sin sin x0 = 2sin x0 cos x0
dt πt 15 30
2 2 – 2 cos 1
30 cos x0 = [if sin x0 ≠ 0]
πt 2
π sin 30 π
= x0 =
3 πt
2 – 2 cos 30 3
Dx(sin x) = cos x, Dx(sin 2x) = 2cos 2x, so at x 0 ,
At 12:15, the string is stretching at the rate of
the tangent lines to y = sin x and y = sin 2x have
π sin π π 1 ⎛ 1⎞
2 = ≈ 0.74 cm/min slopes of m1 = and m2 = 2 ⎜ – ⎟ = –1,
3 2 – 2 cos π 3 2
2
2 ⎝ 2⎠
respectively. From Problem 40 of Section 0.7,
73. The minute hand makes 1 revolution every hour, m – m1
tan θ = 2 where θ is the angle between
so at t minutes after noon it makes an angle of 1 + m1m2
πt
radians with the vertical. Similarly, at t –1 – 1 –3
30 the tangent lines. tan θ = 2 = 2 = –3,
minutes after noon the hour hand makes an angle ( )
1 + 1 (–1)
2
1
2
πt so θ ≈ –1.25. The curves intersect at an angle of
of with the vertical. Thus, by the Law of
360 1.25 radians.
Cosines, the distance between the tips of the
hands is 1 t
76. AB = OA sin
2 2
⎛ πt πt ⎞
s = 62 + 82 – 2 ⋅ 6 ⋅ 8cos ⎜ – ⎟ 1 t 2 t t
⎝ 30 360 ⎠ D = OA cos ⋅ AB = OA cos sin
2 2 2 2
11πt E = D + area (semi-circle)
= 100 – 96 cos 2
360 2 t t 1 ⎛1 ⎞
= OA cos sin + π ⎜ AB ⎟
ds 1 44π 11πt 2 2 2 ⎝2 ⎠
= ⋅ sin
dt 2 100 – 96 cos 11πt 15 360 2 t t 1 2 t
360 = OA cos sin + πOA sin 2
2 2 2 2
22π sin 11πt
= 360 2 t⎛ t 1 t⎞
= OA sin ⎜ cos + π sin ⎟
15 100 – 96 cos 11πt
360 2⎝ 2 2 2⎠
At 12:20, cos 2 t
D
=
ds 22π sin 11π E cos t + 1 π sin t
= 18
≈ 0.38 in./min 2 2
dt 15 100 – 96 cos 11π 2
18 D 1
lim = =1
t →0 + E 1+ 0

D cos(t / 2)
lim = lim
t →π − E t →π cos(t / 2) + π sin(t / 2)
−
2
0
= =0
π
0+
2


77. y = u and u = x 2 81. [ f ( f ( f ( f (0))))]′
Dx y = Du y ⋅ Dx u = f ′( f ( f ( f (0)))) ⋅ f ′( f ( f (0))) ⋅ f ′( f (0)) ⋅ f ′(0)
1 2x x x = 2 ⋅ 2 ⋅2 ⋅ 2 = 16
= ⋅ 2x = = =
2 u 2 x 2 x x
d [2]
82. a. f = f '( f ( x)) ⋅ f '( x)
dx
x2 – 1 d [1]
78. Dx x – 1 = 2
Dx ( x 2 – 1) = f '( f [1] ) ⋅ f ( x)
x2 – 1 dx
x2 – 1 2 x x2 – 1 d [3]
= (2 x) = b. f = f '( f ( f ( x))) ⋅ f '( f ( x)) ⋅ f '( x)
2 2 dx
x –1 x –1
d [1]
= f '( f [2] ( x)) ⋅ f '( f [1] ( x)) ⋅ f ( x)
sin x dx
79. Dx sin x = Dx (sin x)
sin x d [2]
= f '( f [2] ( x)) ⋅ f ( x)
sin x dx
= cos x = cot x sin x
sin x
c. Conjecture:

( ) ( ) ( )
d [n] d [ n −1]
80. a. Dx L x 2 = L ' x 2 Dx x 2 =
1
⋅ 2x =
2 f ( x) = f '( f [ n −1] ( x)) ⋅ f ( x)
x 2 x dx dx

b. Dx L(cos 4 x) = sec4 x Dx (cos 4 x )
= sec4 x(4 cos3 x) Dx (cos x )
= 4sec4 x cos3 x(− sin x)
1
= 4⋅ ⋅ cos3 x ⋅ ( − sin x )
cos 4 x
= –4sec x sin x = −4 tan x

⎛ f ( x) ⎞ ⎛ 1 ⎞
83. Dx ⎜ ⎟ = Dx ⎜ f ( x ) ⋅
⎝ g ( x) ⎠ ⎝ g ( x) ⎠
−1
( −1
) −1
⎟ = Dx f ( x) ⋅ ( g ( x)) = f ( x) Dx ( g ( x)) + ( g ( x)) Dx f ( x) ( )
= f ( x) ⋅ (−1)( g ( x)) −2 Dx g ( x) + ( g ( x)) −1 Dx f ( x) = − f ( x)( g ( x)) −2 Dx g ( x) + ( g ( x))−1 Dx f ( x)
− f ( x) Dx g ( x) Dx f ( x ) − f ( x ) Dx g ( x ) g ( x ) Dx f ( x ) − f ( x ) Dx g ( x ) g ( x ) Dx f ( x )
= 2
+ = + ⋅ = +
g ( x) g ( x) g 2 ( x) g ( x) g ( x) g 2 ( x) g 2 ( x)
g ( x) Dx f ( x) − f ( x) Dx g ( x)
=
g 2 ( x)

( (
84. g ′ ( x ) = f ′ f f ( f ( x ) ) )) f ′ ( f ( f ( x ))) f ′ ( f ( x )) f ′ ( x )
g ′ ( x ) = f ′ ( f ( f ( f ( x )))) f ′ ( f ( f ( x ))) f ′ ( f ( x )) f ′ ( x )
1 1 1 1 1

( )
= f ′ f ( f ( x2 ) ) f ′ ( f ( x2 ) ) f ′ ( x2 ) f ′ ( x1 ) = f ′ ( f ( x1 ) ) f ′ ( x1 ) f ′ ( x2 ) f ′ ( x1 )

= ⎡ f ′ ( x1 ) ⎤ ⎡ f ′ ( x2 ) ⎤
2 2
⎣ ⎦ ⎣ ⎦
( (
g ′ ( x2 ) = f ′ f f ( f ( x2 ) ) ) ) f ′ ( f ( f ( x2 ) ) ) f ′ ( f ( x2 ) ) f ′ ( x2 )
( )
= f ′ f ( f ( x1 ) ) f ′ ( f ( x1 ) ) f ′ ( x1 ) f ′ ( x2 ) = f ′ ( f ( x2 ) ) f ′ ( x2 ) f ′ ( x1 ) f ′ ( x2 )

= ⎡ f ′ ( x1 ) ⎤ ⎡ f ′ ( x2 ) ⎤ = g ′ ( x1 )
2 2
⎣ ⎦ ⎣ ⎦


2.6 Concepts Review dy
3. = 3(3 x + 5) 2 (3) = 9(3x + 5) 2
dx
d3y
1. f ′′′( x), Dx3 y, , y ''' d2y
dx 3 = 18(3 x + 5)(3) = 162 x + 270
dx 2
ds ds d 2 s d3y
2. ; ; = 162
dt dt dt 2 dx3

f ′ (t ) > 0
dy
3. 4. = 5(3 – 5 x)4 (–5) = –25(3 – 5 x)4
dx
4. 0; < 0 d2y
= –100(3 – 5 x)3 (–5) = 500(3 – 5 x)3
dx 2
Problem Set 2.6 d3y
= 1500(3 – 5 x) 2 (–5) = –7500(3 – 5 x)2
3
dx
dy
1. = 3x2 + 6 x + 6
dx dy
2
5. = 7 cos(7 x)
d y dx
= 6x + 6
dx 2 d2y
= –7 2 sin(7 x)
d3y dx 2
=6
dx3 d3y
= –73 cos(7 x) = –343cos(7 x)
3
dx
dy
2. = 5 x 4 + 4 x3
dx
d2y
= 20x 3 +12 x 2
dx 2
d3y
= 60 x 2 + 24 x
3
dx

dy
6. = 3x 2 cos( x3 )
dx
d2y
= 3 x 2 [–3x 2 sin( x3 )] + 6 x cos( x3 ) = –9 x 4 sin( x3 ) + 6 x cos( x3 )
dx 2
d3y
= –9 x 4 cos( x3 )(3 x 2 ) + sin( x3 )(–36 x3 ) + 6 x[– sin( x3 )(3 x 2 )] + 6 cos( x3 )
3
dx
= –27 x 6 cos( x3 ) – 36 x3 sin( x3 ) –18 x3 sin( x3 ) + 6 cos( x3 ) = (6 – 27 x 6 ) cos( x3 ) – 54 x3 sin( x3 )

dy ( x –1)(0) – (1)(1) 1 dy (1 – x )(3) – (3x )(–1) 3
7. = =– 8. = =
2
dx ( x –1) ( x –1)2 dx (1 – x) 2
( x – 1)2
d2y ( x –1)2 (0) – 2( x –1) 2 d2y ( x – 1) 2 (0) – 3[2( x – 1)] 6
=− = = =–
2 4 3 2 4
dx ( x –1) ( x –1) dx ( x – 1) ( x – 1)3
d3y ( x − 1)3 (0) − 2[3( x − 1) 2 ] d3y ( x − 1)3 (0) − 6(3)( x − 1) 2
= =−
dx3 ( x − 1)6 dx3 ( x − 1)6
6 18
=− =
( x − 1) 4
( x − 1) 4


9. f ′( x) = 2 x; f ′′( x) = 2; f ′′(2) = 2 (5 – u )(4u ) – (2u 2 )(–1) 20u – 2u 2
12. f ′(u ) = =
(5 – u ) 2 (5 – u ) 2
10. f ′( x) = 15 x 2 + 4 x + 1
(5 – u )2 (20 – 4u ) – (20u – 2u 2 )2(5 – u )(–1)
f ′′( x) = 30 x + 4 f ′′(u ) =
(5 – u )4
f ′′(2) = 64
100
=
2 (5 – u )3
11. f ′(t ) = –
t2 f ′′(2) =
100
=
100
4 3 27
3
f ′′(t ) =
3
t
4 1
f ′′(2) = =
8 2

13. f ′(θ ) = –2(cos θπ) –3 (– sin θπ)π = 2 π(cos θ π) –3 (sin θ π)
f ′′(θ ) = 2π[(cos θπ) –3 (π)(cos θπ) + (sin θπ)(–3)(cosθπ) –4 (– sin θπ)(π)] = 2π2 [(cos θπ)−2 + 3sin 2 θπ(cosθπ) −4 ]
f ′′(2) = 2π2 [1 + 3(0)(1)] = 2π2

⎛ π ⎞⎛ π ⎞ ⎛π⎞ ⎛ π⎞ ⎛π⎞ ⎛π⎞
14. f ′(t ) = t cos ⎜ ⎟ ⎜ – ⎟ + sin ⎜ ⎟ = ⎜ – ⎟ cos ⎜ ⎟ + sin ⎜ ⎟
⎝ t ⎠⎝ t ⎠
2 ⎝t⎠ ⎝ t⎠ ⎝t⎠ ⎝t⎠
⎛ π⎞⎡ ⎛ π ⎞ ⎛ π ⎞⎤ ⎛ π ⎞ ⎛π⎞ ⎛ π ⎞ ⎛π⎞ π2 ⎛π⎞
f ′′(t ) = ⎜ – ⎟ ⎢ – sin ⎜ ⎟ ⎜ – ⎟ ⎥ + ⎜ ⎟ cos ⎜ ⎟ + ⎜ – ⎟ cos ⎜ ⎟ = – sin ⎜ ⎟
⎝ t ⎠⎣ ⎝ t ⎠ ⎝ t ⎠⎦ ⎝ t ⎠
2 2 ⎝t⎠ ⎝ t ⎠2 ⎝t⎠ t 3 ⎝t⎠
π2 ⎛π⎞ π2
f ′′(2) = – sin ⎜ ⎟ = – ≈ –1.23
8 ⎝2⎠ 8

15. f ′( s ) = s (3)(1 – s 2 )2 (–2 s ) + (1 – s 2 )3 = –6s 2 (1 – s 2 ) 2 + (1 – s 2 )3 = –7 s 6 + 15s 4 – 9 s 2 + 1
f ′′( s ) = –42 s5 + 60 s3 –18s
f ′′(2) = –900

( x –1)2( x + 1) – ( x + 1)2 x2 – 2 x – 3
16. f ′( x) = =
( x –1)2 ( x –1)2
( x –1) 2 (2 x – 2) – ( x 2 – 2 x – 3)2( x –1) ( x –1)(2 x – 2) – ( x 2 – 2 x – 3)(2) 8
f ′′( x) = = =
4 3
( x –1) ( x –1) ( x –1)3
8
f ′′(2) = =8
13

17. Dx ( x n ) = nx n –1 18. Let k < n.
Dx ( x k ) = Dx − k [ Dx ( x k )] = Dx (k !) = 0
n n k
Dx ( x n ) = n(n –1) x n –2
2
so Dx [an x n –1 +…+ a1 x + a0 ] = 0
n
Dx ( x n ) = n(n –1)(n – 2) x n –3
3

Dx ( x n ) = n(n – 1)(n – 2)(n – 3) x n –4
4
19. a. Dx (3x3 + 2 x –19) = 0
4

Dx −1 ( x n ) = n(n –1)(n – 2)(n – 3)...(2) x
n
b. D12 (100 x11 − 79 x10 ) = 0
x
Dx ( x n ) = n(n –1)(n – 2)(n – 3)...2(1) x 0 = n!
n
c. D11 ( x 2 – 3)5 = 0
x


⎛1⎞ 1 b. 3t 2 – 12t > 0
20. Dx ⎜ ⎟ = –
⎝ x⎠ x2 3t(t – 4) > 0; (−∞, 0) ∪ (4, ∞)
2⎛1⎞ 2
Dx ⎜ ⎟ = Dx (– x –2 ) = 2 x –3 =
⎝ x⎠ x3 c. 3t 2 – 12t < 0
3⎛1⎞ 3(2) (0, 4)
Dx ⎜ ⎟ = Dx (2 x –3 ) = –
⎝ x⎠ x4 d. 6t – 12 < 0
4 ⎛ 1 ⎞ 4(3)(2) 6t < 12
Dx ⎜ ⎟ =
⎝ x⎠ x5 t < 2; (−∞, 2)
n ⎛ 1 ⎞ ( −1) n !
n
Dx ⎜ ⎟ = e.
⎝x⎠ x n +1

21. f ′( x) = 3 x 2 + 6 x – 45 = 3( x + 5)( x − 3)
3(x + 5)(x – 3) = 0
x = –5, x = 3 ds
25. a. v(t ) = = 3t 2 –18t + 24
f ′′( x) = 6 x + 6 dt
f ′′(–5) = –24 d 2s
a(t ) = = 6t – 18
f ′′(3) = 24 dt 2

22. g ′(t ) = 2at + b b. 3t 2 –18t + 24 > 0
g ′′(t ) = 2a 3(t – 2)(t – 4) > 0
g ′′(1) = 2a = −4 (−∞, 2) ∪ (4, ∞)
a = −2
g ′(1) = 2a + b = 3 c. 3t 2 –18t + 24 < 0
(2, 4)
2(–2) + b = 3
b=7 d. 6t – 18 < 0
g (1) = a + b + c = 5 6t < 18
( −2 ) + ( 7 ) + c = 5 t < 3; (−∞,3)
c=0 e.
ds
23. a. v(t ) = = 12 – 4t
dt
d 2s
a(t ) = = –4 ds
dt 2 26. a. v(t ) = = 6t 2 – 6
dt
b. 12 – 4t > 0 d 2s
4t < 12 a(t ) = = 12t
dt 2
t < 3; ( −∞,3)
b. 6t 2 – 6 > 0
c. 12 – 4t < 0
6(t + 1)(t – 1) > 0
t > 3; (3, ∞)
(−∞, −1) ∪ (1, ∞)
d. a(t) = –4 < 0 for all t
c. 6t 2 – 6 < 0
e. (–1, 1)

d. 12t < 0
t<0
ds The acceleration is negative for negative t.
24. a. v(t ) = = 3t 2 –12t
dt
d 2s
a(t ) = = 6t –12
dt 2


e. ds
29. v(t ) = = 2t 3 –15t 2 + 24t
dt
d 2s
a(t ) = = 6t 2 – 30t + 24
dt 2
ds 16 6t 2 – 30t + 24 = 0
27. a. v(t ) = = 2t –
dt t2 6(t – 4)(t – 1) = 0
t = 4, 1
d 2s 32
a(t ) = = 2+ v(4) = –16, v(1) = 11
2
dt t3
ds 1
16 30. v(t ) = = (4t 3 – 42t 2 + 120t )
b. 2t – >0 dt 10
t2 d 2s 1
a(t ) = = (12t 2 – 84t + 120)
2t 3 – 16 2 10
> 0; (2, ∞) dt
t2 1
(12t 2 – 84t + 120) = 0
16 10
c. 2t – < 0; (0, 2) 12
t2 (t − 2)(t − 5) = 0
10
32 t = 2, t = 5
d. 2+ <0 v(2) = 10.4, v(5) = 5
t3
2t3 + 32 < 0; The acceleration is not
ds1
t3 31. v1 (t ) = = 4 – 6t
negative for any positive t. dt
ds
e. v2 (t ) = 2 = 2t – 2
dt

a. 4 – 6t = 2t – 2
8t = 6
ds 4
28. a. v(t ) = =1– 3
dt t2 t = sec
4
d 2s 8
a(t ) = =
dt 2
t3 b. 4 – 6t = 2t – 2 ; 4 – 6t = –2t + 2
1 3
4 t= sec and t = sec
b. 1– >0 2 4
t2
t2 – 4 c. 4t – 3t 2 = t 2 – 2t
> 0; (2, ∞)
t2 4t 2 – 6t = 0
2t(2t – 3) = 0
4 3
c. 1– < 0; (0, 2) t = 0 sec and t = sec
2 2
t

8 ds1
d. < 0; The acceleration is not negative for 32. v1 (t ) = = 9t 2 – 24t + 18
3 dt
t
any positive t. ds
v2 (t ) = 2 = –3t 2 + 18t –12
dt
e.
9t 2 – 24t + 18 = –3t 2 + 18t –12
12t 2 – 42t + 30 = 0
2t 2 – 7t + 5 = 0
(2t – 5)(t – 1) = 0
5
t = 1,
2


33. a. v(t) = –32t + 48 37. v(t ) = 3t 2 – 6t – 24
initial velocity = v0 = 48 ft/sec
d 2 3t 2 – 6t – 24
b. –32t + 48 = 0 3t – 6t – 24 = (6t – 6)
3 dt 3t 2 – 6t – 24
t = sec (t – 4)(t + 2)
2 = (6t – 6)
(t – 4)(t + 2)
c. s = –16(1.5) 2 + 48(1.5) + 256 = 292 ft (t – 4)(t + 2) (6t – 6)
<0
(t – 4)(t + 2)
d. –16t + 48t + 256 = 0
2
t < –2, 1 < t < 4; (−∞, −2) ∪ (1, 4)
–48 ± 48 – 4(–16)(256)
2
t= ≈ –2.77, 5.77 38. Point slowing down when
–32
The object hits the ground at t = 5.77 sec. d
v(t ) < 0
dt
e. v(5.77) ≈ –137 ft/sec; d v(t ) a (t )
speed = −137 = 137 ft/sec. v(t ) =
dt v(t )
v (t ) a(t )
34. v(t) = 48 –32t < 0 when a(t) and v(t) have opposite
v (t )
a. 48 – 32t = 0 signs.
t = 1.5
s = 48(1.5) –16(1.5)2 = 36 ft 39. Dx (uv) = uv′ + u ′v
Dx (uv) = uv ′′ + u ′v ′ + u ′v ′ + u ′′v
2
b. v(1) = 16 ft/sec upward
= uv ′′ + 2u ′v ′ + u ′′v
c. 48t –16t 2 = 0 Dx (uv) = uv ′′′ + u ′v′′ + 2(u ′v′′ + u ′′v′) + u ′′v′ + u ′′′v
3

–16t(–3 + t) = 0 = uv′′′ + 3u ′v′′ + 3u ′′v′ + u ′′′v
t = 3 sec n
⎛n⎞
Dx (uv) =
n
∑ ⎜ k ⎟ Dx −k (u ) Dx (v)
n k
35. v(t ) = v0 – 32t k =0 ⎝ ⎠
v0 – 32t = 0 ⎛ n⎞
where ⎜ ⎟ is the binomial coefficient
v0 ⎝ k⎠
t=
32 n!
.
2 (n – k )!k !
⎛v ⎞ ⎛v ⎞
v0 ⎜ 0 ⎟ –16 ⎜ 0 ⎟ = 5280
⎝ 32 ⎠ ⎝ 32 ⎠
⎛ 4⎞ 4
40. Dx ( x 4 sin x ) = ⎜ ⎟ Dx ( x 4 ) Dx (sin x)
4 0
v02 v0 2 ⎝ 0⎠
– = 5280
32 64 ⎛ 4⎞ 3 4 1 ⎛ 4⎞ 2
+ ⎜ ⎟ Dx ( x ) Dx (sin x) + ⎜ ⎟ Dx ( x 4 ) Dx (sin x)
2
v02 ⎝1⎠ ⎝ 2⎠
= 5280
64 ⎛ 4⎞ ⎛ 4⎞ 0
v0 = 337,920 ≈ 581 ft/sec + ⎜ ⎟ D1 ( x 4 ) Dx (sin x) + ⎜ ⎟ Dx ( x 4 ) Dx (sin x)
x
3 4
⎝ 3⎠ ⎝ 4⎠
36. v(t ) = v0 + 32t = 24sin x + 96 x cos x − 72 x 2 sin x
v0 + 32t = 140 −16 x3 cos x + x 4 sin x
v0 + 32(3) = 140
v0 = 44
s = 44(3) + 16(3) 2 = 276 ft


41. a. 4. 2 x + 2α 2 yDx y = 0
2x x
Dx y = – =–
2α y 2
α2y

5. x(2 y ) Dx y + y 2 = 1
1 – y2
Dx y =
2 xy

b. f ′′′ (2.13) ≈ –1. 2826 6. 2 x + 2 x 2 Dx y + 4 xy + 3 x Dx y + 3 y = 0

42. a. Dx y (2 x 2 + 3 x) = –2 x – 4 xy – 3 y
–2 x – 4 xy – 3 y
Dx y =
2 x2 + 3x

7. 12 x 2 + 7 x(2 y ) Dx y + 7 y 2 = 6 y 2 Dx y
12 x 2 + 7 y 2 = 6 y 2 Dx y – 14 xyDx y
12 x 2 + 7 y 2
Dx y =
b. f ′′′(2.13) ≈ 0.0271 6 y 2 – 14 xy

8. x 2 Dx y + 2 xy = y 2 + x(2 y ) Dx y
2.7 Concepts Review
x 2 Dx y – 2 xyDx y = y 2 – 2 xy
9 y 2 – 2 xy
1.
3
x –3 Dx y =
x 2 – 2 xy
dy
2. 3 y 2 1
dx 9. ⋅ (5 x Dx y + 5 y ) + 2 Dx y
2 5 xy

3. x(2 y )
dy
+ y2 + 3y2
dy dy
– = 3x2 = 2 y Dx y + x(3 y 2 ) Dx y + y 3
dx dx dx 5x
Dx y + 2 Dx y – 2 y Dx y – 3 xy 2 Dx y
p p q –1 5 2 2 5 xy
4. x ; ( x – 5 x)2 / 3 (2 x – 5) 5y
q 3 = y3 –
2 5 xy
Problem Set 2.7 y3 –
5y
2 5 xy
1. 2 y Dx y – 2 x = 0 Dx y =
5x + 2 – 2 y – 3 xy 2
2 5 xy
2x x
Dx y = =
2y y
1
10. x Dx y + y + 1 = x Dx y + y
2. 18 x + 8 y Dx y = 0 2 y +1
–18 x 9x x
Dx y = =– Dx y – x Dx y = y – y + 1
8y 4y 2 y +1
y – y +1
3. x Dx y + y = 0 Dx y =
x –x
y 2 y +1
Dx y = –
x


11. x Dx y + y + cos( xy )( x Dx y + y ) = 0 2 –1/ 3 2 –1/ 3
17. x – y y′ – 2 y′ = 0
x Dx y + x cos( xy ) Dx y = – y – y cos( xy ) 3 3
– y – y cos( xy ) y 2 –1/ 3 ⎛2 ⎞
Dx y = =– x = y ′ ⎜ y –1/ 3 + 2 ⎟
x + x cos( xy ) x 3 ⎝3 ⎠
2 x –1/ 3

12. – sin( xy 2 )(2 xy Dx y + y 2 ) = 2 yDx y + 1 y′ = 3
2 y –1/ 3 + 2
3
–2 xy sin( xy 2 ) Dx y – 2 y Dx y = 1 + y 2 sin( xy 2 ) 2
1
1 + y sin( xy )
2 2 At (1, –1), y ′ = 3
=
Dx y = 4 2
–2 xy sin( xy 2 ) – 2 y 3
1
Tangent line: y + 1 = ( x –1)
13. x y ′ + 3 x y + y + 3xy y ′ = 0
3 2 3 2 2

y ′( x3 + 3xy 2 ) = –3 x 2 y – y 3 1
18. y ′ + 2 xyy ′ + y 2 = 0
2 3 2 y
–3 x y – y
y′ =
x3 + 3 xy 2 ⎛ 1 ⎞
y′ ⎜ + 2 xy ⎟ = – y 2
36 9 ⎜2 y ⎟
At (1, 3), y ′ = – =– ⎝ ⎠
28 7
– y2
9 y′ =
Tangent line: y – 3 = – ( x – 1) 1 + 2 xy
7 2 y
–1 2
At (4, 1), y ′ = =–
14. x 2 (2 y ) y ′ + 2 xy 2 + 4 xy ′ + 4 y = 12 y ′ 17 17
2
y ′(2 x 2 y + 4 x – 12) = –2 xy 2 – 4 y 2
Tangent line: y –1 = – ( x – 4)
–2 xy 2 – 4 y – xy 2 – 2 y 17
y′ = =
2 x 2 y + 4 x – 12 x 2 y + 2 x – 6
dy 1
At (2, 1), y ′ = –2 19. = 5x2 / 3 +
dx 2 x
Tangent line: y – 1 = –2( x – 2)
dy 1 –2 / 3 1
15. cos( xy )( xy ′ + y ) = y ′ 20. = x – 7 x5 / 2 = – 7 x5 / 2
dx 3 3 2
y ′[ x cos( xy ) – 1] = – y cos( xy ) 3 x
– y cos( xy ) y cos( xy )
y′ = = 21.
dy 1 –2 / 3 1 –4 / 3
= x – x =
1
–
1
x cos( xy ) – 1 1 – x cos( xy ) dx 3 3 3 3
3 x2 3 x4
⎛π ⎞
At ⎜ , 1⎟ , y ′ = 0
⎝2 ⎠ dy 1 1
22. = (2 x + 1) –3 / 4 (2) =
⎛ π⎞ dx 4
Tangent line: y – 1 = 0 ⎜ x – ⎟ 2 (2 x + 1)3
4
⎝ 2⎠
y=1 dy 1
23. = (3 x 2 – 4 x) –3 / 4 (6 x – 4)
dx 4
16. y ′ + [– sin( xy 2 )][2 xyy ′ + y 2 ] + 6 x = 0
6x – 4 3x – 2
= =
y ′[1 – 2 xy sin( xy 2 )] = y 2 sin( xy 2 ) – 6 x 2 3
4
4 (3 x – 4 x) 2 (3 x 2 – 4 x)3
4
y 2 sin( xy 2 ) – 6 x
y′ =
1 – 2 xy sin( xy 2 ) 24.
dy 1 3
= ( x – 2 x) –2 / 3 (3 x 2 – 2)
6 dx 3
At (1, 0), y ′ = – = –6
1
dy d
Tangent line: y – 0 = –6(x – 1) 25. = [( x3 + 2 x)−2 / 3 ]
dx dx
2 6 x2 + 4
= – ( x3 + 2 x) –5 / 3 (3 x 2 + 2) = −
3 3 3 ( x 3 + 2 x )5


dy 5 dx dx
26. = – (3 x – 9) –8 / 3 (3) = –5(3 x – 9) –8 / 3 34. 1 = cos( x 2 )(2 x ) + 6x2
dx 3 dy dy
dx 1
dy 1 =
27. = (2 x + cos x) dy 2 x cos( x 2 ) + 6 x 2
dx 2 x 2 + sin x
2 x + cos x 35. y
= 5
2 x 2 + sin x (x + 2)2 + y2 = 1

dy 1
28. = [ x 2 (– sin x) + 2 x cos x]
dx 2 x 2 cos x −5 5 x

2 x cos x – x 2 sin x
=
2 x 2 cos x −5

dy d dy
29. = [( x 2 sin x) –1/ 3 ] 2x + 4 + 2 y =0
dx dx dx
1 dy 2x + 4 x+2
= – ( x 2 sin x) –4 / 3 ( x 2 cos x + 2 x sin x) =− =−
3 dx 2y y
x 2 cos x + 2 x sin x The tangent line at ( x0 , y0 ) has equation
=–
2
33 ( x sin x) 4 x +2
y – y0 = − 0 ( x – x0 ) which simplifies to
y0
dy 1 2 x0 – yy0 – 2 x – xx0 + y02 + x02 = 0. Since
30. = (1 + sin 5 x) –3 / 4 (cos 5 x)(5)
dx 4
( x0 , y0 ) is on the circle, x0 2 + y02 = –3 – 4 x0 ,
5cos 5 x
= so the equation of the tangent line is
4 4 (1 + sin 5 x)3 – yy0 – 2 x0 – 2 x – xx0 = 3.
3
dy [1 + cos( x 2 + 2 x)]–3 / 4 [– sin( x 2 + 2 x)(2 x + 2)] If (0, 0) is on the tangent line, then x0 = – .
31. = 2
dx 4 Solve for y0 in the equation of the circle to get
( x + 1) sin( x 2 + 2 x)
=− y0 = ±
3
. Put these values into the equation of
2 [1 + cos( x + 2 x )]
4 2 3
2
the tangent line to get that the tangent lines are
dy (tan 2 x + sin 2 x) –1/ 2 (2 tan x sec 2 x + 2 sin x cos x) 3 y + x = 0 and 3 y – x = 0.
32. =
dx 2
tan x sec2 x + sin x cos x 36. 16( x 2 + y 2 )(2 x + 2 yy ′) = 100(2 x – 2 yy ′)
=
tan 2 x + sin 2 x 32 x3 + 32 x 2 yy ′ + 32 xy 2 + 32 y 3 y ′ = 200 x – 200 yy ′

ds y ′(4 x 2 y + 4 y 3 + 25 y ) = 25 x – 4 x3 – 4 xy 2
33. s 2 + 2 st + 3t 2 = 0
dt 25 x – 4 x3 – 4 xy 2
ds – s – 3t 2
s + 3t
2 2 2 y′ =
= =− 4 x 2 y + 4 y 3 + 25 y
dt 2 st 2 st
1
dt dt The slope of the normal line = –
s 2 + 2st + 3t 2 =0 y′
ds ds
4 x 2 y + 4 y 3 + 25 y
dt 2
( s + 3t 2 ) = –2 st =
ds 4 x3 + 4 xy 2 – 25 x
dt 2 st 65 13
=− At (3, 1), slope = =
ds s + 3t 2
2 45 9
13
Normal line: y – 1 = ( x – 3)
9


37. a. xy ′ + y + 3 y 2 y ′ = 0 72 y 5 − 6 x 4 y − 24 x 2 y 3
y ′′(6 y 2 – x 2 ) =
y ′( x + 3 y 2 ) = – y (6 y 2 – x 2 ) 2
y 72 y 5 − 6 x 4 y − 24 x 2 y 3
y′ = – y ′′ =
x + 3y2 (6 y 2 – x 2 )3
−120
At (2, 1), y ′′ = = −15
⎛ –y ⎞ ⎛ –y ⎞ 8
xy ′′ + ⎜ ⎟+⎜ + 3 y 2 y ′′
⎟ ⎜ x + 3 y2 ⎟
b.
⎜ x + 3y2 ⎟
⎝ ⎠ ⎝ ⎠
40. 2 x + 2 yy ′ = 0
2
⎛ –y ⎞ 2x x
+6 y ⎜ ⎟ =0 y′ = – =–
⎜ x + 3 y2 ⎟ 2y y
⎝ ⎠
2y 6 y3 2 + 2[ yy ′′ + ( y ′)2 ] = 0
xy ′′ + 3 y 2 y ′′ – + =0
x + 3 y2 ( x + 3 y 2 )2 ⎛ x⎞
2
2 + 2 yy ′′ + 2 ⎜ – ⎟ = 0
2y 6 y3 ⎝ y⎠
y ′′( x + 3 y 2 ) = –
x + 3y2 ( x + 3 y 2 )2 2 x2
2 yy ′′ = −2 −
y ′′( x + 3 y 2 ) =
2 xy y2
(x + 3y ) 2 2
1 x2 y 2 + x2
2 xy y ′′ = − − =−
y ′′ = y y3 y3
( x + 3 y 2 )3 25
At (3, 4), y ′′ = −
64
38. 3x 2 – 8 yy ′ = 0
3x2 41. 3x 2 + 3 y 2 y ′ = 3( xy ′ + y )
y′ =
8y y ′(3 y 2 – 3x) = 3 y – 3 x 2
6 x – 8( yy ′′ + ( y ′)2 ) = 0 y – x2
2
y′ =
⎛ 3x2 ⎞ y2 – x
6 x – 8 yy ′′ – 8 ⎜ ⎟ =0
⎜ 8y ⎟ ⎛3 3⎞
⎝ ⎠ At ⎜ , ⎟ , y ′ = –1
⎝2 2⎠
9 x4
6 x – 8 yy ′′ – =0 Slope of the normal line is 1.
8 y2 3 ⎛ 3⎞
Normal line: y – = 1⎜ x – ⎟ ; y = x
48 xy 2 − 9 x 4 2 ⎝ 2⎠
= 8 yy ′′
8 y2 This line includes the point (0, 0).
48 xy 2 – 9 x 4 42. xy ′ + y = 0
y ′′ =
64 y 3 y
y′ = –
x
39. 2( x 2 y ′ + 2 xy ) – 12 y 2 y ′ = 0 2 x − 2 yy ′ = 0
2 x 2 y ′ – 12 y 2 y ′ = –4 xy x
y′ =
2 xy y
y′ =
6 y2 – x2 The slopes of the tangents are negative
reciprocals, so the hyperbolas intersect at right
2( x 2 y ′′ + 2 xy ′ + 2 xy ′ + 2 y ) – 12[ y 2 y ′′ + 2 y ( y ′) 2 ] = 0 angles.
2 x 2 y ′′ − 12 y 2 y ′′ = −8 xy ′ − 4 y + 24 y ( y ′)2
16 x 2 y 96 x 2 y3
y ′′(2 x 2 – 12 y 2 ) = − – 4y +
6 y2 – x2 (6 y 2 − x 2 )2
12 x 4 y + 48 x 2 y 3 − 144 y5
y ′′(2 x 2 – 12 y 2 ) =
(6 y 2 – x 2 ) 2


43. Implicitly differentiate the first equation. 45. x 2 – x(2 x) + 2(2 x) 2 = 28
4 x + 2 yy ′ = 0
7 x 2 = 28
2x
y′ = – x2 = 4
y
x = –2, 2
Implicitly differentiate the second equation. Intersection point in first quadrant: (2, 4)
2 yy ′ = 4 ′
y1 = 2
2 ′ ′
2 x – xy2 – y + 4 yy2 = 0
y′ =
y ′
y2 (4 y – x) = y – 2 x
Solve for the points of intersection.
y – 2x
2 x2 + 4 x = 6 ′
y2 =
4y – x
2( x 2 + 2 x – 3) = 0 At (2, 4): m1 = 2, m2 = 0
(x + 3)(x – 1) = 0
0–2
x = –3, x = 1 tan θ = = –2; θ = π + tan –1 (–2) ≈ 2.034
x = –3 is extraneous, and y = –2, 2 when x = 1. 1 + (0)(2)
The graphs intersect at (1, –2) and (1, 2).
At (1, –2): m1 = 1, m2 = –1 46. The equation is mv 2 – mv0 = kx0 – kx 2 .
2 2

At (1, 2): m1 = –1, m2 = 1 Differentiate implicitly with respect to t to get
dv dx dx
44. Find the intersection points: 2mv = –2kx . Since v = this simplifies
dt dt dt
x2 + y 2 = 1 → y 2 = 1 − x2 dv dv
to 2mv = –2kxv or m = – kx.
( x − 1)2 + y 2 = 1 dt dt

( x − 1)2 + (1 − x 2 ) = 1 47. x 2 – xy + y 2 = 16 , when y = 0,
1
x2 − 2 x + 1 + 1 − x2 = 1 ⇒ x= x 2 = 16
2 x = –4, 4
⎛1 3⎞ ⎛1 3⎞ The ellipse intersects the x-axis at (–4, 0) and
Points of intersection: ⎜ ,
⎜ 2 2 ⎟ and ⎜ 2 , – 2 ⎟
⎟ ⎜ ⎟ (4, 0).
⎝ ⎠ ⎝ ⎠
2 x – xy ′ – y + 2 yy ′ = 0
Implicitly differentiate the first equation.
2 x + 2 yy ′ = 0 y ′(2 y – x) = y – 2 x
x y – 2x
y′ = – y′ =
y 2y – x
Implicitly differentiate the second equation. At (–4, 0), y ′ = 2
2( x –1) + 2 yy ′ = 0 At (4, 0), y ′ = 2
1– x Tangent lines: y = 2(x + 4) and y = 2(x – 4)
y′ =
y
⎛1 3⎞ 1 1
⎜ 2 2 ⎟ : m1 = – 3 , m2 = 3
At ⎜ , ⎟
⎝ ⎠
1 + 1 2
π
tan θ = 3 3
= 3 = 3 → θ=
( )( )
1+ 1 − 1
3 3
2
3
3

⎛1 3⎞ 1 1
At ⎜ , –
⎜2 ⎟ : m1 =
⎟ , m2 = –
⎝ 2 ⎠ 3 3
− 1 − 1 − 2
tan θ = 3 3
= 3
=− 3
1+ 1
( )( )
–
3
1
3
2
3

2π
θ=
3


dx dx Problem Set 2.8
48. x 2 + 2 xy – 2 xy – y 2 =0
dy dy
dx
dx 1. V = x3 ; =3
(2 xy – y 2 ) = 2 xy – x 2 ; dt
dy
dV dx
dx 2 xy – x 2 = 3x2
= dt dt
dy 2 xy – y 2 dV
When x = 12, = 3(12)2 (3) = 1296 in.3/s.
2 xy – x 2 dt
= 0 if x(2y – x) = 0, which occurs
2 xy – y 2
4 3 dV
x 2. V = πr ; =3
when x = 0 or y = . There are no points on 3 dt
2 dV dr
x = 4πr 2
x y – xy = 2 where x = 0. If y = , then
2 2
dt dt
2
dr
2
x3 x3 x3 When r = 3, 3 = 4π(3)2 .
2⎛x⎞ ⎛ x⎞
2 = x ⎜ ⎟ – x⎜ ⎟ = – = so x = 2, dt
⎝2⎠ ⎝2⎠ 2 4 4 dr 1
= ≈ 0.027 in./s
2
y = = 1. dt 12π
2
The tangent line is vertical at (2, 1). dx
3. y 2 = x 2 + 12 ; = 400
dt
dy dy x
49. 2 x + 2 y = 0; =– dy dx
dx dx y 2y = 2x
dt dt
x0 dy x dx
The tangent line at ( x0 , y0 ) has slope – , = mi/hr
y0 dt y dt
hence the equation of the tangent line is
dy 5
x When x = 5, y = 26, = (400)
y – y0 = – 0 ( x – x0 ) which simplifies to dt 26
y0
≈ 392 mi/h.
yy0 + xx0 – ( x02 + y02 ) = 0 or yy0 + xx0 = 1
1 r 3 3h
since ( x0 , y0 ) is on x 2 + y 2 = 1 . If (1.25, 0) is 4. V = πr 2 h; = ; r =
3 h 10 10
on the tangent line through ( x0 , y0 ) , x0 = 0.8. 2
1 ⎛ 3h ⎞ 3πh3 dV
Put this into x 2 + y 2 = 1 to get y0 = 0.6, since V = π⎜ ⎟ h = ; = 3, h = 5
3 ⎝ 10 ⎠ 100 dt
y0 > 0. The line is 6y + 8x = 10. When x = –2,
dV 9πh 2 dh
13 13 =
y = , so the light bulb must be units high. dt 100 dt
3 3
9π(5)2 dh
When h = 5, 3 =
100 dt
dh 4
= ≈ 0.42 cm/s
dt 3π
2.8 Concepts Review
dx dy
1.
du
;t = 2 5. s 2 = ( x + 300)2 + y 2 ;
= 300, = 400,
dt dt dt
ds dx dy
2s = 2( x + 300) + 2 y
2. 400 mi/hr dt dt dt
ds dx dy
3. negative s = ( x + 300) + y
dt dt dt
4. negative; positive When x = 300, y = 400, s = 200 13 , so
ds
200 13 = (300 + 300)(300) + 400(400)
dt
ds
≈ 471 mi/h
dt


dy hx 40 x
6. y 2 = x 2 + (10)2 ; =2 11. V = (20); = , x = 8h
dt 2 5 h
dy dx dV
2y = 2x V = 10h(8h) = 80h 2 ; = 40
dt dt dt
When y = 25, x ≈ 22.9, so dV dh
= 160h
dx y dy 25 dt dt
= ≈ (2) ≈ 2.18 ft/s
dt x dt 22.9 dh
When h = 3, 40 = 160(3)
dt
dx
7. 202 = x 2 + y 2 ; =1 dh 1
dt = ft/min
dt 12
dx dy
0 = 2x + 2 y
dt dt dx
12. y = x 2 – 4; =5
dt
When x = 5, y = 375 = 5 15 , so
dy 1 dx x dx
dy x dx 5 = (2 x) =
=– =– (1) ≈ –0.258 ft/s dt 2 x 2 – 4 dt x 2 – 4 dt
dt y dt 5 15
dy 3 15
The top of the ladder is moving down at When x = 3, = (5) = ≈ 6.7 units/s
0.258 ft/s. dt 2
3 –4 5

dV dh dr
8. = –4 ft3/h; V = πhr 2 ; = –0.0005 ft/h 13. A = πr 2 ; = 0.02
dt dt dt
V dA dV V dh dA dr
A = πr 2 = = Vh –1 , so = h –1 – . = 2πr
h dt dt h 2 dt dt dt
When h = 0.001 ft, V = π(0.001)(250) 2 = 62.5π When r = 8.1,
dA
= 2π(0.02)(8.1) = 0.324π
dA dt
and = 1000(–4) –1, 000, 000(62.5π)(–0.0005) ≈ 1.018 in.2/s
dt
= –4000 + 31,250 π ≈ 94,175 ft2/h. dx dy
(The height is decreasing due to the spreading of 14. s 2 = x 2 + ( y + 48) 2 ; = 30, = 24
dt dt
the oil rather than the bacteria.)
ds dx dy
2s = 2 x + 2( y + 48)
1 d r dt dt dt
9. V = πr 2 h; h = = , r = 2h
3 4 2 ds dx dy
s = x + ( y + 48)
1 4 dV dt dt dt
V = π(2h) 2 h = πh3 ; = 16
3 3 dt At 2:00 p.m., x = 3(30) = 90, y = 3(24) = 72,
dV dh so s = 150.
= 4πh 2 ds
dt dt (150) = 90(30) + (72 + 48)(24)
dt
dh
When h = 4, 16 = 4π(4) 2 ds 5580
dt = = 37.2 knots/h
dt 150
dh 1
= ≈ 0.0796 ft/s
dt 4π

dx
10. y 2 = x 2 + (90)2 ; =5
dt
dy dx
2y = 2x
dt dt
When y = 150, x = 120, so
dy x dx 120
= = (5) = 4 ft/s
dt y dt 150


( )
15. Let x be the distance from the beam to the point 2
1
opposite the lighthouse and θ be the angle dθ
6
2⎛1⎞ 1
between the beam and the line from the =– ⎜ ⎟=– .
dt 6 2 ⎝ 2⎠ 24
lighthouse to the point opposite.
Chris must lift his head at the rate of
x dθ
tan θ = ; = 2(2π) = 4π rad/min, 1
1 dt rad/s.
24
dθ dx
sec2 θ =
dt dt 18. Let θ be the measure of the vertex angle, a be the
1 1 5 measure of the equal sides, and b be the measure
At x = , θ = tan –1 and sec2 θ = .
2 2 4 θ
of the base. Observe that b = 2a sin and the
dx 5 2
= (4π) ≈ 15.71 km/min
dt 4 θ
height of the triangle is a cos .
2
4000 1⎛ θ ⎞⎛ θ⎞ 1
16. tan θ = A = ⎜ 2a sin ⎟ ⎜ a cos ⎟ = a 2 sin θ
x 2⎝ 2 ⎠⎝ 2⎠ 2
dθ 4000 dx 1 dθ 1
sec2 θ =− A = (100)2 sin θ = 5000sin θ ; =
dt x 2 dt 2 dt 10
1 dθ 1 4000 dA dθ
When θ = , = and x = ≈ 7322. = 5000 cos θ
2 dt 10 tan 1
2
dt dt
π dA ⎛ π ⎞⎛ 1 ⎞
dx 1 ⎛ 1 ⎞ ⎡ (7322) 2 ⎤ When θ = , = 5000 ⎜ cos ⎟ ⎜ ⎟ = 250 3
≈ sec2 ⎜ ⎟ ⎢− ⎥ 6 dt ⎝ 6 ⎠ ⎝ 10 ⎠
dt 2 ⎝ 10 ⎠ ⎢ 4000 ⎥
⎣ ⎦
≈ 433 cm 2 min .
≈ –1740 ft/s or –1186 mi/h
The plane’s ground speed is 1186 mi/h.
19. Let p be the point on the bridge directly above
17. a. Let x be the distance along the ground from the railroad tracks. If a is the distance between p
the light pole to Chris, and let s be the da
and the automobile, then = 66 ft/s. If l is the
distance from Chris to the tip of his shadow. dt
6 30 x distance between the train and the point directly
By similar triangles, = , so s =
s x+s 4 below p, then
dl
= 88 ft/s. The distance from the
ds 1 dx dx dt
and = . = 2 ft/s, hence
dt 4 dt dt train to p is 1002 + l 2 , while the distance from
ds 1 p to the automobile is a. The distance between
= ft/s no matter how far from the light
dt 2 the train and automobile is
pole Chris is. 2
D = a 2 + ⎛ 1002 + l 2 ⎞ = a 2 + l 2 + 1002 .
⎜ ⎟
b. Let l = x + s, then ⎝ ⎠
dl dx ds 1 5 dD 1 ⎛ da dl ⎞
= + = 2 + = ft/s. = ⋅ ⎜ 2a + 2l ⎟
dt dt dt 2 2 dt 2 a 2 + l 2 + 1002 ⎝ dt dt ⎠

c. The angular rate at which Chris must lift his a da + l dl
= dt dt
. After 10 seconds, a = 660
head to follow his shadow is the same as the a 2 + l 2 + 1002
rate at which the angle that the light makes
and l = 880, so
with the ground is decreasing. Let θ be the
dD 660(66) + 880(88)
angle that the light makes with the ground at = ≈ 110 ft/s.
the tip of Chris' shadow. dt 6602 + 8802 + 1002
6 dθ 6 ds
tan θ = so sec2 θ =– and
s dt s 2 dt
dθ 6 cos 2 θ ds ds 1
=– . = ft/s
dt s2 dt dt 2
π
When s = 6, θ = , so
4


1 h 48 10 + s
20. V = πh ⋅ (a 2 + ab + b 2 ); a = 20, b = + 20, By similar triangles, =
3 4 2 s
64 – 16t
1 ⎛ h 2 ⎞ 10t 2 – 40
V = πh ⎜ 400 + 5h + 400 + + 10h + 400 ⎟ (for t > 1), so s = .
3 ⎝ ⎜ 16 ⎟ 1 – t2
⎠
1 ⎛ 3⎞ ds 20t (1 – t 2 ) – (10t 2 – 40)(–2t ) 60t
= π ⎜ 1200h + 15h 2 + ⎟
h = =–
⎜
3 ⎝ 16 ⎟ dt 2 2
(1 – t ) (1 – t 2 )2
⎠
ds 120
dV 1 ⎛ 2⎞
3h dh The ball hits the ground when t = 2, =– .
= π ⎜ 1200 + 30h + ⎟ dt 9
dt 3 ⎜ ⎝ 16 ⎟ dt
⎠ 120
The shadow is moving ≈ 13.33 ft/s.
dV 9
When h = 30 and = 2000,
dt
1 ⎛ 675 ⎞ dh 3025π dh ⎛ h⎞
2000 = π ⎜1200 + 900 + ⎟ = 24. V = πh 2 ⎜ r – ⎟ ; r = 20
3 ⎝ 4 ⎠ dt 4 dt ⎝ 3⎠
dh 320 ⎛ h⎞ π
= ≈ 0.84 cm/min. V = πh 2 ⎜ 20 – ⎟ = 20πh 2 − h3
dt 121π ⎝ 3⎠ 3
dV dh
= (40πh − πh 2 )
⎡ h ⎤ dV
21. V = πh 2 ⎢ r – ⎥ ; = –2, r = 8 dt dt
⎣ 3 ⎦ dt dh
At 7:00 a.m., h = 15, ≈ −3, so
πh3 πh3 dt
V = πrh 2 – = 8πh 2 –
3 3 dV
= (40π(15) − π(15) 2 )(−3) ≈ −1125π ≈ −3534.
dV dh dh dt
= 16πh – πh 2
dt dt dt Webster City residents used water at the rate of
dh 2400 + 3534 = 5934 ft3/h.
When h = 3, –2 = [16π(3) – π(3)2 ]
dt 25. Assuming that the tank is now in the shape of an
dh –2 upper hemisphere with radius r, we again let t be
= ≈ –0.016 ft/hr
dt 39π the number of hours past midnight and h be the
height of the water at time t. The volume, V, of
22. s 2 = a 2 + b 2 − 2ab cos θ ; water in the tank at that time is given by
2 π
dθ π 11π V = π r 3 − ( r − h) 2 ( 2r + h )
a = 5, b = 4, = 2π – = rad/h 3 3
dt 6 6
16000 π
s 2 = 41 – 40 cos θ and so V = π − (20 − h)2 ( 40 + h )
3 3
ds dθ
2s = 40sin θ from which
dt dt dV π dh 2π dh
π = − (20 − h)2 + (20 − h) ( 40 + h )
At 3:00, θ = and s = 41 , so dt 3 dt 3 dt
2 dV
ds ⎛ π ⎞ ⎛ 11π ⎞ 220π At t = 7 , ≈ −525π ≈ −1649
2 41 = 40sin ⎜ ⎟ ⎜ ⎟= dt
dt ⎝ 2 ⎠⎝ 6 ⎠ 3 Thus Webster City residents were using water at
ds the rate of 2400 + 1649 = 4049 cubic feet per
≈ 18 in./hr
dt hour at 7:00 A.M.

23. Let P be the point on the ground where the ball 26. The amount of water used by Webster City can
hits. Then the distance from P to the bottom of be found by:
the light pole is 10 ft. Let s be the distance usage = beginning amount + added amount
between P and the shadow of the ball. The height − remaining amount
of the ball t seconds after it is dropped is
Thus the usage is
64 –16t 2 .
≈ π (20)2 (9) + 2400(12) − π (20)2 (10.5) ≈ 26,915 ft 3
over the 12 hour period.


dx
27. a. Let x be the distance from the bottom of the wall to the end of the ladder on the ground, so = 2 ft/s. Let y
dt
y 18 216
be the height of the opposite end of the ladder. By similar triangles, = , so y = .
12 144 + x 2
144 + x 2
dy 216 dx 216 x dx
=– 2x =–
dt 2(144 + x )
2 3/ 2 dt (144 + x )
2 3 / 2 dt

dy 216(4 3)
When the ladder makes an angle of 60° with the ground, x = 4 3 and =– ⋅ 2 = –1.125 ft/s.
dt (144 + 48)3 / 2

d2y d ⎛ 216 x dx ⎞ d ⎛ 216 x ⎞ dx 216 x d2x
b. = ⎜– ⎟ = ⎜– ⎟ – ⋅
dt 2 dt ⎜ (144 + x 2 )3 / 2 dt ⎟ dt ⎜ (144 + x 2 )3 / 2
⎝ ⎠ ⎝
⎟ dt (144 + x 2 )3 / 2 dt 2
⎠
dx d2x
Since = 2, = 0, thus
dt dt 2

d2y
⎡ –216(144 + x 2 )3 / 2 dx + 216 x 3
=⎢ dt 2 ( ) 144 + x 2 (2 x) dx ⎤ dx
dt ⎥
dt 2 ⎢ (144 + x )
2 3 ⎥ dt
⎢
⎣ ⎥
⎦
2 2
–216(144 + x 2 ) + 648 x 2 ⎛ dx ⎞ 432 x 2 – 31,104 ⎛ dx ⎞
= ⎜ ⎟ = ⎜ ⎟
(144 + x 2 )5 / 2 ⎝ dt ⎠ (144 + x 2 )5 / 2 ⎝ dt ⎠
When the ladder makes an angle of 60° with the ground,
d 2 y 432 ⋅ 48 – 31,104 2
= (2) ≈ –0.08 ft/s2
dt 2 (144 + 48)5 / 2

28. a. If the ball has radius 6 in., the volume of the dV
water in the tank is 29. = k (4πr 2 )
dt
3
πh3 4 ⎛ 1 ⎞
V = 8πh 2 – – π⎜ ⎟ 4 3
3 3 ⎝2⎠ a. V= πr
3
πh3 π dV dr
= 8πh 2 – – = 4πr 2
3 6 dt dt
dV dh dh dr
= 16πh – πh 2 k (4πr 2 ) = 4πr 2
dt dt dt dt
dh dr
This is the same as in Problem 21, so
dt
is =k
dt
again –0.016 ft/hr.
b. If the ball has radius 2 ft, and the height of b. If the original volume was V0 , the volume
the water in the tank is h feet with 2 ≤ h ≤ 3 , 8
after 1 hour is V0 . The original radius
the part of the ball in the water has volume 27
4 ⎡ 4 – h ⎤ (6 – h)h 2 π
π(2)3 – π(4 – h) 2 ⎢ 2 – = . was r0 = 3
3
3 ⎣ 3 ⎥ ⎦ 3 4π
V0 while the radius after 1
The volume of water in the tank is
8 3 2 dr
πh3 (6 – h)h 2 π hour is r1 = 3 V0 ⋅ = r0 . Since is
V = 8πh 2 – – = 6h 2 π 27 4π 3 dt
3 3 dr 1
dV dh constant, = – r0 unit/hr. The snowball
= 12hπ dt 3
dt dt will take 3 hours to melt completely.
dh 1 dV
=
dt 12hπ dt
dh 1
When h = 3, = (–2) ≈ –0.018 ft/hr.
dt 36π

Instructor's Resource Manual Section 2.8 137

30. PV = k Problem Set 2.9
dV dP
P +V =0 1. dy = (2x + 1)dx
dt dt
dP
At t = 6.5, P ≈ 67,≈ –30, V = 300 2. dy = (21x 2 + 6 x)dx
dt
dV V dP 300
=– =– (–30) ≈ 134 in.3/min 3. dy = –4(2 x + 3) –5 (2)dx = –8(2 x + 3) –5 dx
dt P dt 67

31. Let l be the distance along the ground from the 4. dy = –2(3 x 2 + x + 1) –3 (6 x + 1)dx
brother to the tip of the shadow. The shadow is = –2(6 x + 1)(3x 2 + x + 1) –3 dx
3 5
controlled by both siblings when = or
l l+4
5. dy = 3(sin x + cos x)2 (cos x – sin x) dx
l = 6. Again using similar triangles, this occurs
y 6
when = , so y = 40. Thus, the girl controls 6. dy = 3(tan x + 1) 2 (sec2 x)dx
20 3
the tip of the shadow when y ≥ 40 and the boy = 3sec2 x(tan x + 1)2 dx
controls it when y < 40.
Let x be the distance along the ground from the 3
dx 7. dy = – (7 x 2 + 3x –1) –5 / 2 (14 x + 3)dx
light pole to the girl. = –4 2
dt 3
4 = − (14 x + 3)(7 x 2 + 3 x − 1) −5 2 dx
20 5 2
When y ≥ 40, = or y = x.
y y–x 3
1
When y < 40,
20
=
3
or y =
20
( x + 4). 8. dy = 2( x10 + sin 2 x )[10 x9 + ⋅ (cos 2 x )(2)]dx
y y – ( x + 4) 17 2 sin 2 x
x = 30 when y = 40. Thus, ⎛ cos 2 x ⎞ 10
= 2 ⎜ 10 x9 + ⎟ ( x + sin 2 x )dx
⎧ 4 ⎝ sin 2 x ⎠
⎪ 3x if x ≥ 30
⎪
y=⎨ 3 2
⎪ 20 ( x + 4) if x < 30 9. ds = (t – cot t + 2)1/ 2 (2t + csc2 t )dt
⎪ 17
⎩ 2
and 3
= (2t + csc2 t ) t 2 – cot t + 2dt
⎧ 4 dx 2
if x ≥ 30
dy ⎪ 3 dt
⎪
=⎨ 10. a. dy = 3 x 2 dx = 3(0.5)2 (1) = 0.75
dt ⎪ 20 dx
if x < 30
⎪ 17 dt
⎩
Hence, the tip of the shadow is moving at the rate b. dy = 3x 2 dx = 3(–1)2 (0.75) = 2.25
4 16
of (4) = ft/s when the girl is at least 30 feet 11.
3 3
from the light pole, and it is moving
20 80
(4) = ft/s when the girl is less than 30 ft
17 17
from the light pole.

2.9 Concepts Review

1. f ′( x)dx

2. Δy; dy dx 0.5
12. a. dy = – =– = –0.5
2
x (1)2
3. Δx is small.
dx 0.75
4. larger ; smaller b. dy = – =– = –0.1875
2
x (–2)2


13. 1 –2 / 3 1
20. y = 3 x ; dy = x dx = dx;
3 3 2
3 x
x = 27, dx = –0.09
1
dy = (–0.09) ≈ –0.0033
33 (27)2
3
26.91 ≈ 3 27 + dy = 3 – 0.0033 = 2.9967

4 3
21. V = πr ; r = 5, dr = 0.125
3
dV = 4πr 2 dr = 4π(5)2 (0.125) ≈ 39.27 cm3
14. a. Δy = (1.5)3 – (0.5)3 = 3.25
22. V = x3 ; x = 3 40, dx = 0.5
b. Δy = (–0.25)3 – (–1)3 = 0.984375 dV = 3 x 2 dx = 3( 3 40)2 (0.5) ≈ 17.54 in.3

1 1 1 4 3
15. a. Δy = – =– 23. V = πr ; r = 6 ft = 72in., dr = –0.3
1.5 1 3 3
dV = 4πr 2 dr = 4π(72)2 (–0.3) ≈ –19,543
1 1
b. Δy = + = –0.3 4
–1.25 2 V≈ π(72)3 –19,543
3
16. a. Δy = [(2.5) 2 – 3] – [(2) 2 – 3] = 2.25 ≈ 1,543,915 in 3 ≈ 893 ft 3
dy = 2xdx = 2(2)(0.5) = 2
24. V = πr 2 h; r = 6 ft = 72in., dr = −0.05,
b. Δy = [(2.88) – 3] – [(3) – 3] = –0.7056
2 2
h = 8ft = 96in.
dy = 2xdx = 2(3)(–0.12) = –0.72 dV = 2πrhdr = 2π(72)(96)(−0.05) ≈ −2171in.3
About 9.4 gal of paint are needed.
17. a. Δy = [(3) 4 + 2(3)] – [(2)4 + 2(2)] = 67
dy = (4 x3 + 2)dx = [4(2)3 + 2](1) = 34 25. C = 2π r ; r = 4000 mi = 21,120,000 ft, dr = 2
dC = 2π dr = 2π (2) = 4π ≈ 12.6 ft
b. Δy = [(2.005)4 + 2(2.005)] – [(2)4 + 2(2)]
L
≈ 0.1706 26. T = 2π ; L = 4, dL = –0.03
32
dy = (4 x3 + 2)dx = [4(2)3 + 2](0.005) = 0.17
2π 1 π
dT = ⋅ ⋅ dL = dL
1 2 L 32 32 L
18. y = x ; dy = dx; x = 400, dx = 2 32
2 x π
1 dT = (–0.03) ≈ –0.0083
dy = (2) = 0.05 32(4)
2 400 The time change in 24 hours is
402 ≈ 400 + dy = 20 + 0.05 = 20.05 (0.0083)(60)(60)(24) ≈ 717 sec

1 4 3 4
19. y = x ; dy = dx; x = 36, dx = –0.1 27. V = πr = π(10)3 ≈ 4189
2 x 3 3
1 dV = 4πr 2 dr = 4π(10) 2 (0.05) ≈ 62.8 The
dy = (–0.1) ≈ –0.0083
2 36 volume is 4189 ± 62.8 cm3.
35.9 ≈ 36 + dy = 6 – 0.0083 = 5.9917 The absolute error is ≈ 62.8 while the relative
error is 62.8 / 4189 ≈ 0.015 or 1.5% .


28. V = πr 2 h = π(3) 2 (12) ≈ 339 33. Using the approximation
f ( x + Δx) ≈ f ( x) + f '( x)Δx
dV = 24πrdr = 24π(3)(0.0025) ≈ 0.565
we let x = 3.05 and Δx = −0.05 . We can rewrite
The volume is 339 ± 0.565 in.3 the above form as
The absolute error is ≈ 0.565 while the relative f ( x) ≈ f ( x + Δx) − f '( x)Δx
error is 0.565 / 339 ≈ 0.0017 or 0.17% .
which gives
f (3.05) ≈ f (3) − f '(3.05)(−0.05)
29. s = a 2 + b 2 – 2ab cos θ
1
= 8 + (0.05) = 8.0125
= 1512 + 1512 – 2(151)(151) cos 0.53 ≈ 79.097 4
s = 45, 602 – 45, 602 cos θ
34. From similar triangles, the radius at height h is
1
ds = ⋅ 45, 602sin θ dθ 2 1 4
h. Thus, V = πr 2 h = πh3 , so
2 45, 602 – 45, 602 cos θ 5 3 75
22,801sin θ 4
= dθ dV = πh 2 dh. h = 10, dh = –1:
45, 602 – 45, 602 cosθ 25
22,801sin 0.53 4
= (0.005) ≈ 0.729 dV = π(100)(−1) ≈ −50 cm3
45, 602 – 45, 602 cos 0.53 25
s ≈ 79.097 ± 0.729 cm The ice cube has volume 33 = 27 cm3 , so there is
The absolute error is ≈ 0.729 while the relative room for the ice cube without the cup
error is 0.729 / 79.097 ≈ 0.0092 or 0.92% . overflowing.

1 1 4
30. A = ab sin θ = (151)(151) sin 0.53 ≈ 5763.33 35. V = πr 2 h + πr 3
2 2 3
22,801 4
A= sin θ ;θ = 0.53, dθ = 0.005 V = 100πr 2 + πr 3 ; r = 10, dr = 0.1
2 3
22,801 dV = (200πr + 4πr 2 )dr
dA = (cos θ )dθ
2 = (2000π + 400π)(0.1) = 240π ≈ 754 cm3
22,801
= (cos 0.53)(0.005) ≈ 49.18
2 dm
A ≈ 5763.33 ± 49.18 cm2 36. The percent increase in mass is
m
.
The absolute error is ≈ 49.18 while the relative –3 / 2
error is 49.18 / 5763.33 ≈ 0.0085 or 0.85% . m ⎛ v2 ⎞ ⎛ 2v ⎞
dm = – 0 ⎜ 1 – ⎟ ⎜ – 2 ⎟ dv
2 ⎜ c2 ⎟
⎝ ⎠ ⎝ c ⎠
31. y = 3 x 2 – 2 x + 11; x = 2, dx = 0.001 –3 / 2
dy = (6x – 2)dx = [6(2) – 2](0.001) = 0.01 m v ⎛ v2 ⎞
= 0 ⎜1 – ⎟ dv
d2y c2 ⎜ c2
⎝
⎟
⎠
= 6, so with Δx = 0.001,
dx 2 dm v ⎛ v 2 ⎞
–1
v ⎛ c2 ⎞
1 = ⎜1 – 2 ⎟ dv = 2 ⎜ 2 2 ⎟ dv
Δy – dy ≤ (6)(0.001) 2 = 0.000003 m c2 ⎜ c ⎟
⎝ ⎠ c ⎜c −v ⎟
⎝ ⎠
2
v
= dv
32. Using the approximation c − v2
2
f ( x + Δx) ≈ f ( x) + f '( x)Δx v = 0.9c, dv = 0.02c
we let x = 1.02 and Δx = −0.02 . We can rewrite dm 0.9c 0.018
the above form as = (0.02c) = ≈ 0.095
m c 2 − 0.81c 2 0.19
f ( x) ≈ f ( x + Δx) − f '( x)Δx
The percent increase in mass is about 9.5.
which gives
f (1.02) ≈ f (1) − f '(1.02)( −0.02)
= 10 + 12(0.02) = 10.24


37. f ( x) = x 2 ; f '( x) = 2 x; a = 2 39. h( x) = sin x; h '( x) = cos x; a = 0
The linear approximation is then The linear approximation is then
L( x) = f (2) + f '(2)( x − 2) L( x) = 0 + 1( x − 0) = x
= 4 + 4( x − 2) = 4 x − 4

40. F ( x ) = 3x + 4; F '( x) = 3; a = 3
38. g ( x) = x cos x; g '( x) = − x sin x + 2 x cos x
2 2 The linear approximation is then
L( x) = 13 + 3( x − 3) = 13 + 3 x − 9
a =π /2
The linear approximation is then = 3x + 4
2
⎛π ⎞ ⎛ π⎞
L( x) = 0 + − ⎜ ⎟ ⎜ x − ⎟
⎝2⎠ ⎝ 2⎠
π2 π3
=− x+
4 8
π ⎛
2
π⎞
L( x) = 0 + − ⎜x− ⎟
4 ⎝ 2⎠
π2 π3
=− x+
4 8


41. f ( x ) = 1 − x2 ; 45. f (x ) = mx + b; f ′(x ) = m
The linear approximation is then
( )
−1/ 2
f ′( x) =
1
1 − x2 ( −2 x ) L(x ) = ma + b + m(x − a ) = am + b + mx − ma
2 = mx + b f ( x ) = L(x )
−x
= , a=0
1 − x2 1
46. L ( x ) − f ( x ) = a + ( x − a) − x
The linear approximation is then 2 a
L ( x ) = 1 + 0 ( x − 0) = 1 x a x−2 a x +a
= − x+ =
2 a 2 2 a

( )
2
x− a
= ≥0
2 a

47. The linear approximation to f ( x ) at a is
L( x) = f (a) + f '(a)( x − a)
x = a 2 + 2a ( x − a )
42. g ( x ) = ;
1 − x2 = 2ax − a 2
(1 − x ) − x ( −2 x ) = 1 + x
2 2 Thus,
( )
1
g '( x) = ,a = f ( x) − L( x) = x 2 − 2ax − a 2
(1 − x ) 2 2
(1 − x )
2 2 2

The linear approximation is then = x 2 − 2ax + a 2
2 20 ⎛ 1 ⎞ 20 = ( x − a)2
L(x ) = +
4
⎜x− ⎟ = x−
3 9 ⎝ 2⎠ 9 9 ≥0

48. f (x ) = (1 + x )α , f ′(x ) = α (1 + x )α −1 , a = 0
L(x ) = 1 + α (x ) = αx + 1
y

5

43. h(x ) = x sec x; h ′(x ) = sec x + x sec x tan x, a = 0
L(x ) = 0 + 1(x − 0) = x −5 5 x

−5
α = −2
y

44. G (x ) = x + sin 2 x; G ′(x ) = 1 + 2 cos 2 x , a = π / 2 5

π ⎛ π⎞
L(x ) = + (− 1)⎜ x − ⎟ = − x + π
2 ⎝ 2⎠ −5 5 x

−5
α = −1


49. a. lim ε ( h ) = lim ( f ( x + h ) − f ( x ) − f ′ ( x ) h )
y
h→0 h →0
5 = f ( x) − f ( x) − f ′( x) 0 = 0

ε (h) ⎡ f ( x + h) − f ( x) ⎤
b. lim = lim ⎢ − f ′ ( x )⎥
h→0 h
−5 5 x
⎣ h ⎦
= f ′( x) − f ′( x) = 0

−5
α = −0.5
y
2.10 Chapter Review

5 Concepts Test

1. False: If f ( x) = x3 , f '( x) = 3 x 2 and the
tangent line y = 0 at x = 0 crosses the
−5 5 x curve at the point of tangency.

2. False: The tangent line can touch the curve
−5 at infinitely many points.
α =0
y 3. True: mtan = 4 x3 , which is unique for each
value of x.
5
4. False: mtan = – sin x, which is periodic.

5. True: If the velocity is negative and
increasing, the speed is decreasing.
−5 5 x
6. True: If the velocity is negative and
decreasing, the speed is increasing.
−5
α = 0.5 7. True: If the tangent line is horizontal, the
y
slope must be 0.

8. False: f ( x) = ax 2 + b, g ( x) = ax 2 + c,
5
b ≠ c . Then f ′( x) = 2ax = g ′( x), but
f(x) ≠ g(x).

−5 5
9. True: Dx f ( g ( x)) = f ′( g ( x)) g ′( x); since
x
g(x) = x, g ′( x) = 1, so
Dx f ( g ( x)) = f ′( g ( x)).
−5
α =1 10. False: Dx y = 0 because π is a constant, not
y a variable.

5
11. True: Theorem 3.2.A

12. True: The derivative does not exist when the
tangent line is vertical.

−5 5 x 13. False: ( f ⋅ g )′( x) = f ( x) g ′( x) + g ( x) f ′( x)

14. True: Negative acceleration indicates
−5 decreasing velocity.
α =2


15. True: If f ( x) = x3 g ( x), then 29. True: Dx (sin x ) = cos x;

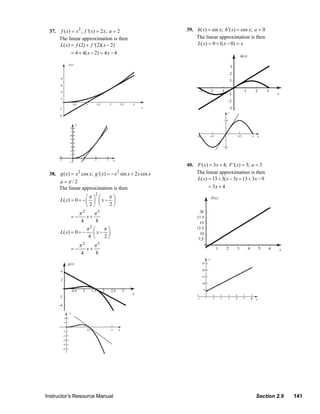
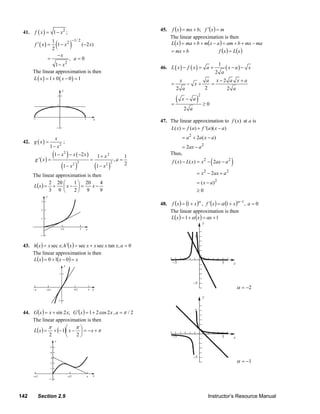
Dx f ( x) = x3 g ′( x) + 3x 2 g ( x) Dx (sin x ) = – sin x;
2

= x 2 [ xg ′( x) + 3 g ( x)]. Dx (sin x) = – cos x;
3

Dx (sin x) = sin x;
4

16. False: Dx y = 3 x 2 ; At (1, 1): Dx (sin x) = cos x
5

mtan = 3(1) = 3 2

Tangent line: y – 1 = 3(x – 1) 30. False: Dx (cos x ) = – sin x;
Dx (cos x) = – cos x;
2
17. False: Dx y = f ( x) g ′( x) + g ( x) f ′( x)
Dx (cos x) = sin x;
3
Dx y = f ( x) g ′′( x) + g ′( x) f ′( x)
2

+ g ( x) f ′′( x) + f ′( x) g ′( x) Dx (cos x ) = Dx [ Dx (cos x)] = Dx (sin x)
4 3

= f ( x) g ′′( x) + 2 f ′( x) g ′( x) + f ′′( x) g ( x) Since D1+3 (cos x) = D1 (sin x),
x x
Dx +3 (cos x) = Dx (sin x).
n n

18. True: The degree of y = ( x + x) is 24, so
3 8

Dx y = 0.
25 tan x 1 sin x
31. True: lim = lim
x →0 3 x 3 x →0 x cos x
f ( x) = ax n ; f ′( x) = anx n –1 1 1
19. True: = ⋅1 =
3 3
f ( x) g ( x) f ′( x) – f ( x) g ′( x)
20. True: Dx = ds
g ( x) g 2 ( x) 32. True: v= = 15t 2 + 6 which is greater
dt
than 0 for all t.
21. True: h′( x) = f ( x) g ′( x) + g ( x) f ′( x)
h′(c) = f (c) g ′(c) + g (c) f ′(c) 4 3
33. True: V= πr
= f(c)(0) + g(c)(0) = 0 3

(π)
dV dr
= 4πr 2
⎛π⎞ sin x – sin
dt dt
22. True: f ′ ⎜ ⎟ = lim 2
⎝ 2 ⎠ x→ π x– π dV dr 3
2 2 If = 3, then = so
sin x –1 dt dt 4πr 2
= lim
x→ π x– π
2
dr
> 0.
2 dt
d 2r 3 dr d 2r
23. True: D 2 (kf ) = kD 2 f and =– so <0
dt 2 2πr 3 dt dt 2
D2 ( f + g ) = D2 f + D2 g
d 2h
24. True: h′( x) = f ′( g ( x)) ⋅ g ′( x) 34. True: When h > r, then >0
dt 2
h′(c) = f ′( g (c)) ⋅ g ′(c) = 0
4 3
25. True: ( f g )′(2) = f ′( g (2)) ⋅ g ′(2) 35. True: V= πr , S = 4πr 2
3
= f ′(2) ⋅ g ′(2) = 2 ⋅ 2 = 4
dV = 4πr 2 dr = S ⋅ dr
If Δr = dr, then dV = S ⋅ Δr
26. False: Consider f ( x) = x . The curve
always lies below the tangent. 36. False: dy = 5 x 4 dx, so dy > 0 when dx > 0,
27. False: The rate of volume change depends but dy < 0 when dx < 0.
on the radius of the sphere.
37. False: The slope of the linear approximation
dr is equal to
28. True: c = 2π r ; =4 f '(a ) = f '(0) = − sin(0) = 0 .
dt
dc dr
= 2π = 2π(4) = 8π
dt dt


Sample Test Problems

3( x + h)3 – 3x3 9 x 2 h + 9 xh 2 + 3h3
1. a. f ′( x) = lim = lim = lim (9 x 2 + 9 xh + 3h 2 ) = 9 x 2
h →0 h h →0 h h →0

[2( x + h)5 + 3( x + h)] – (2 x5 + 3 x) 10 x 4 h + 20 x3 h 2 + 20 x 2 h3 + 10 xh 4 + 2h5 + 3h
b. f ′( x) = lim = lim
h →0 h h →0 h
= lim (10 x 4 + 20 x3 h + 20 x 2 h 2 + 10 xh3 + 2h 4 + 3) = 10 x 4 + 3
h →0

1 – 31x
3( x + h ) ⎡ h ⎤1 ⎛ 1 ⎞ 1
c. f ′( x) = lim = lim ⎢ – ⎥ = lim – ⎜ 3x( x + h) ⎟ = – 2
h →0 h h →0 ⎣ 3( x + h) x ⎦ h h →0 ⎝ ⎠ 3x

⎡⎛ 1 1 ⎞ 1⎤ ⎡ 3x 2 + 2 – 3( x + h) 2 – 2 1 ⎤
d. f ′( x) = lim ⎢⎜ – ⎟ ⎥ = lim ⎢ ⋅ ⎥
h →0 ⎢⎜ 3( x + h) 2 + 2 3 x 2 + 2 ⎟ h ⎥
⎠ ⎦ h→0 ⎢ (3( x + h) + 2)(3x + 2) h ⎥
2 2
⎣⎝ ⎣ ⎦
⎡ –6 xh – 3h 2 1⎤ –6 x – 3h 6x
= lim ⎢ ⋅ ⎥ = lim =–
h→0 ⎢ (3( x + h) + 2)(3 x + 2) h ⎥
2 2 h →0 (3( x + h) 2 + 2)(3 x 2 + 2) (3 x + 2)2
2
⎣ ⎦

3( x + h) – 3 x ( 3x + 3h – 3x )( 3x + 3h + 3 x )
e. f ′( x) = lim = lim
h →0 h h →0 h( 3 x + 3h + 3x )
3h 3 3
= lim = lim =
h →0 h( 3 x + 3h + 3 x ) h →0 3x + 3h + 3x 2 3x

sin[3( x + h)] – sin 3x sin(3x + 3h) – sin 3 x
f. f ′( x) = lim = lim
h →0 h h →0 h
sin 3 x cos 3h + sin 3h cos 3 x – sin 3x sin 3 x(cos 3h –1) sin 3h cos 3 x
= lim = lim + lim
h →0 h h →0 h h →0 h
cos 3h –1 sin 3h sin 3h
= 3sin 3 x lim + cos 3 x lim = (3sin 3x)(0) + (cos 3 x)3 lim = (cos 3x)(3)(1) = 3cos 3 x
h →0 3h h →0 h h →0 3h

⎛ ( x + h) 2 + 5 – x 2 + 5 ⎞ ⎛ ( x + h) 2 + 5 + x 2 + 5 ⎞
( x + h) 2 + 5 – x 2 + 5 ⎜ ⎟⎜ ⎟
g. f ′( x) = lim = lim ⎝ ⎠⎝ ⎠
h →0 h h →0
h ⎛ ( x + h) 2 + 5 + x 2 + 5 ⎞
⎜ ⎟
⎝ ⎠
2 xh + h 2 2x + h 2x x
= lim = lim = =
h→0
h ⎛ ( x + h) 2 + 5 + x 2 + 5 ⎞ h→0 ( x + h) + 5 + x + 5 2 x +5 x +5
2 2 2 2
⎜ ⎟
⎝ ⎠

cos[π( x + h)] – cos πx cos(πx + πh) – cos πx cos πx cos πh – sin πx sin πh – cos πx
h. f ′( x) = lim = lim = lim
h →0 h h→0 h h→0 h
⎛ 1 – cos πh ⎞ ⎛ sin πh ⎞
= lim ⎜ – π cos πx ⎟ − lim ⎜ π sin πx ⎟ = (–π cos πx)(0) – (π sin πx) = – π sin πx
h→0 ⎝ πh ⎠ h→0 ⎝ πh ⎠

2t 2 – 2 x 2 2(t – x)(t + x)
2. a. g ′( x) = lim = lim
= 2 lim (t + x) = 2(2 x) = 4 x
t→x


(t 3 + t ) – ( x3 + x) t 3 + C – x3 + C
b. g ′( x) = lim g. g ′( x) = lim
(t – x)(t + tx + x ) + (t – x)
2 2
⎛ t 3 + C – x3 + C ⎞ ⎛ t 3 + C + x3 + C ⎞
= lim ⎜ ⎟⎜ ⎟
t→x
= lim ⎝ ⎠⎝ ⎠
t–x
= lim (t 2 + tx + x 2 + 1) = 3x 2 + 1 t→x ⎛ t 3 + C + x3 + C ⎞
(t – x) ⎜ ⎟
t→x ⎝ ⎠
t 3 – x3
1– 1
x–t = lim
g ′( x) = lim = lim t→x
(t – x) ⎛ t 3 + C + x3 + C ⎞
t x
c. ⎜ ⎟
t→x t–x t → x tx(t – x) ⎝ ⎠
= lim
–1
=–
1 t 2 + tx + x 2 3x 2
= lim =
t → x tx x2 t→x t 3 + C + x3 + C 2 x3 + C
⎡⎛ 1 1 ⎞ ⎛ 1 ⎞⎤
d. g ′( x) = lim ⎢⎜ – ⎟⎜ ⎟⎥ h. g ′( x) = lim
cos 2t – cos 2 x
t → x ⎣⎝ t 2 + 1 x 2 + 1 ⎠ ⎝ t – x ⎠ ⎦ t→x t–x
x2 – t 2 Let v = t – x, then t = v + x and as
= lim t → x, v → 0.
t → x (t 2 + 1)( x 2 + 1)(t – x)
cos 2t – cos 2 x cos 2(v + x) – cos 2 x
–( x + t )(t – x) lim = lim
= lim t→x t–x v →0 v
+ 1)( x 2 + 1)(t – x)
t → x (t 2
cos 2v cos 2 x – sin 2v sin 2 x – cos 2 x
–( x + t ) 2x = lim
= lim =– v →0 v
t → x (t 2 + 1)( x 2 + 1) ( x + 1)2
2
⎡ cos 2v –1 sin 2v ⎤
= lim ⎢ 2 cos 2 x – 2sin 2 x
v →0 ⎣ 2v 2v ⎥ ⎦
e. g ′( x ) = lim
t– x = 2 cos 2 x ⋅ 0 – 2sin 2 x ⋅1 = –2sin 2 x
t→x t – x Other method:
( t – x )( t + x ) Use the subtraction formula
= lim cos 2t − cos 2 x = −2sin(t + x) sin(t − x).
t→x (t – x)( t + x )
t–x 1 3. a. f(x) = 3x at x = 1
= lim = lim
t → x (t – x)( t + x ) t→x t+ x
1 b. f ( x) = 4 x3 at x = 2
=
2 x
c. f ( x) = x3 at x = 1
sin πt – sin πx
f. g ′( x) = lim
t→x t–x d. f(x) = sin x at x = π
Let v = t – x, then t = v + x and as
t → x, v → 0. e. f ( x) =
4
at x
sin πt – sin πx sin π(v + x) – sin πx x
lim = lim
t→x t–x v →0 v
f. f(x) = –sin 3x at x
sin πv cos πx + sin πx cos πv – sin πx
= lim
v →0 v π
g. f(x) = tan x at x =
⎡ sin πv cos πv –1 ⎤ 4
= lim ⎢ π cos πx + π sin πx
v →0 ⎣ πv πv ⎥ ⎦
1
= π cos πx ⋅1 + π sin πx ⋅ 0 = π cos πx h. f ( x) = at x = 5
Other method: x
Use the subtraction formula
π(t + x) π(t − x) f ′(2) ≈ –
3
sin πt – sin πx = 2 cos sin 4. a.
2 2 4

3
b. f ′(6) ≈
2


6– 3 9 d ⎛ 4 x 2 – 2 ⎞ ( x3 + x)(8 x) – (4 x 2 – 2)(3 x 2 + 1)
c. Vavg = 2 = 11. ⎜ ⎟=
7–3 8 dx ⎜ x3 + x ⎟
⎝ ⎠ ( x3 + x ) 2
−4 x 4 + 10 x 2 + 2
d =
d. f (t 2 ) = f ′(t 2 )(2t ) ( x3 + x ) 2
dt
⎛2⎞ 8
At t = 2, 4 f ′(4) ≈ 4 ⎜ ⎟ = 1
⎝3⎠ 3 12. Dt (t 2t + 6) = t (2) + 2t + 6
2 2t + 6
d 2 t
e. [ f (t )] = 2 f (t ) f ′(t ) = + 2t + 6
dt 2t + 6
At t = 2,
⎛ 3⎞ d ⎛ 1 ⎞ d 2
2 f (2) f ′(2) ≈ 2(2) ⎜ – ⎟ = –3 13. ⎜ ⎟ = ( x + 4) –1/ 2
⎝ 4⎠ dx ⎝ x + 4 ⎟ dx
⎜ 2
⎠
1 2
d = – ( x + 4) –3 / 2 (2 x)
f. ( f ( f (t ))) = f ′( f (t )) f ′(t ) 2
dt
x
At t = 2, f ′( f (2)) f ′(2) = f ′(2) f ′(2) =–
⎛ 3 ⎞⎛ 3 ⎞ 9 ( x + 4)3
2
≈ ⎜ – ⎟⎜ – ⎟ =
⎝ 4 ⎠ ⎝ 4 ⎠ 16
d x2 – 1 d 1 d −1 2 1
14. = = x =−
5. Dx (3x ) = 15 x
5 4
dx x –x3 dx x dx 2 x3 2

6. Dx ( x3 – 3 x 2 + x –2 ) = 3 x 2 – 6 x + (–2) x –3 15. Dθ (sin θ + cos3 θ ) = cos θ + 3cos 2 θ (– sin θ )
= 3x 2 – 6 x – 2 x –3 = cosθ – 3sin θ cos 2 θ
Dθ (sin θ + cos3 θ )
2
7. Dz ( z + 4 z + 2 z ) = 3z + 8 z + 2
3 2 2
= – sin θ – 3[sin θ (2)(cos θ )(– sin θ ) + cos3 θ ]
⎛ 3 x – 5 ⎞ ( x 2 + 1)(3) – (3 x – 5)(2 x) = – sin θ + 6sin 2 θ cos θ – 3cos3 θ
8. Dx ⎜ ⎟=
⎝ x2 + 1 ⎠ ( x 2 + 1)2
d
−3 x 2 + 10 x + 3 16. [sin(t 2 ) – sin 2 (t )] = cos(t 2 )(2t ) – (2sin t )(cos t )
= dt
( x 2 + 1) 2 = 2t cos(t 2 ) – sin(2t )

⎛ 4t − 5 ⎞ (6t 2 + 2t )(4) – (4t – 5)(12t + 2)
9. Dt ⎜ ⎟= 17. Dθ [sin(θ 2 )] = cos(θ 2 )(2θ ) = 2θ cos(θ 2 )
⎝ 6t 2 + 2t ⎠ (6t 2 + 2t )2
−24t 2 + 60t + 10 d
(cos3 5 x) = (3cos 2 5 x)(– sin 5 x )(5)
= 18.
(6t 2 + 2t ) 2 dx
= –15cos 2 5 x sin 5 x
2
10. Dx (3x + 2) 2 / 3 = (3 x + 2) –1/ 3 (3)
3
= 2(3 x + 2) –1/ 3
2
Dx (3x + 2) 2 / 3 = – (3x + 2) –4 / 3 (3)
2
3
= –2(3x + 2) –4 / 3


d
19. [sin 2 (sin(πθ ))] = 2sin(sin(πθ )) cos(sin(πθ ))(cos(πθ ))(π) = 2π sin(sin(πθ )) cos(sin(πθ )) cos(πθ )
dθ

d
20. [sin 2 (cos 4t )] = 2sin(cos 4t ) ( cos(cos 4t ) ) (– sin 4t )(4) = –8sin(cos 4t ) cos(cos 4t ) sin 4t
dt

21. Dθ tan 3θ = (sec 2 3θ )(3) = 3sec 2 3θ

d ⎛ sin 3 x ⎞ (cos 5 x 2 )(cos 3 x)(3) – (sin 3 x)(– sin 5 x 2 )(10 x ) 3cos 5 x 2 cos 3 x + 10 x sin 3x sin 5 x 2
22. ⎜ ⎟= =
dx ⎝ cos 5 x 2 ⎠ cos 2 5 x 2 cos 2 5 x 2

23. f ′( x) = ( x 2 –1)2 (9 x 2 – 4) + (3 x3 – 4 x)(2)( x 2 –1)(2 x) = ( x 2 –1)2 (9 x 2 – 4) + 4 x( x 2 –1)(3 x3 – 4 x)
f ′(2) = 672

24. g ′( x) = 3cos 3 x + 2(sin 3 x)(cos 3 x)(3) = 3cos 3x + 3sin 6 x
g ′′( x) = –9sin 3 x + 18cos 6 x
g ′′(0) = 18

d ⎛ cot x ⎞ (sec x 2 )(– csc 2 x) – (cot x)(sec x 2 )(tan x 2 )(2 x) – csc2 x – 2 x cot x tan x 2
25. ⎜ ⎟= =
dx ⎝ sec x 2 ⎠ sec 2 x 2 sec x 2

⎛ 4t sin t ⎞ (cos t – sin t )(4t cos t + 4sin t ) – (4t sin t )(– sin t – cos t )
26. Dt ⎜ ⎟=
⎝ cos t – sin t ⎠ (cos t – sin t )2
4t cos 2 t + 2sin 2t – 4sin 2 t + 4t sin 2 t 4t + 2sin 2t – 4sin 2 t
= =
(cos t – sin t ) 2 (cos t – sin t )2

27. f ′( x) = ( x – 1)3 2(sin πx – x)(π cos πx – 1) + (sin πx – x) 2 3( x – 1)2
= 2( x – 1)3 (sin πx – x)(π cos πx – 1) + 3(sin πx – x) 2 ( x – 1) 2
f ′(2) = 16 − 4π ≈ 3.43

28. h′(t ) = 5(sin(2t ) + cos(3t )) 4 (2 cos(2t ) – 3sin(3t ))
h′′(t ) = 5(sin(2t ) + cos(3t )) 4 (−4sin(2t ) – 9 cos(3t )) + 20(sin(2t ) + cos(3t ))3 (2 cos(2t ) – 3sin(3t )) 2
h′′(0) = 5 ⋅14 ⋅ (−9) + 20 ⋅13 ⋅ 22 = 35

29. g ′(r ) = 3(cos 2 5r )(– sin 5r )(5) = –15cos 2 5r sin 5r
g ′′(r ) = –15[(cos 2 5r )(cos 5r )(5) + (sin 5r )2(cos 5r )(– sin 5r )(5)] = –15[5cos3 5r – 10(sin 2 5r )(cos 5r )]
g ′′′(r ) = –15[5(3)(cos 2 5r )(– sin 5r )(5) − (10sin 2 5r )(− sin 5r )(5) − (cos 5r )(20sin 5r )(cos 5r )(5)]
= –15[−175(cos 2 5r )(sin 5r ) + 50sin 3 5r ]
g ′′′(1) ≈ 458.8

30. f ′(t ) = h′( g (t )) g ′(t ) + 2 g (t ) g ′(t )

31. G ′( x ) = F ′(r ( x ) + s ( x))(r ′( x) + s ′( x)) + s ′( x)
G ′′( x) = F ′(r ( x) + s ( x))(r ′′( x) + s ′′( x)) + (r ′( x) + s ′( x)) F ′′(r ( x) + s ( x))(r ′( x) + s ′( x)) + s ′′( x)
= F ′(r ( x) + s ( x))(r ′′( x ) + s ′′( x)) + (r ′( x) + s ′( x))2 F ′′(r ( x) + s ( x)) + s ′′( x)


32. F ′( x) = Q ′( R ( x)) R ′( x) = 3[ R ( x)]2 (– sin x) b. 128t – 16t 2 = 0
–16t(t – 8) = 0
= –3cos 2 x sin x
The object hits the ground when t = 8s
v = 128 – 32(8) = –128 ft/s
33. F ′( z ) = r ′( s ( z )) s ′( z ) = [3cos(3s ( z ))](9 z 2 )
= 27 z 2 cos(9 z 3 ) 39. s = t 3 – 6t 2 + 9t
ds
v(t ) = = 3t 2 – 12t + 9
dy dt
34. = 2( x – 2)
dx d 2s
2x – y + 2 = 0; y = 2x + 2; m = 2 a(t ) = = 6t –12
dt 2
1
2( x – 2) = –
2 a. 3t 2 – 12t + 9 < 0
7
x= 3(t – 3)(t – 1) < 0
4 1 < t < 3; (1,3)
2
⎛7 ⎞ 1 ⎛7 1 ⎞
y = ⎜ – 2⎟ = ; ⎜ , ⎟
⎝4 ⎠ 16 ⎝ 4 16 ⎠ b. 3t 2 – 12t + 9 = 0
3(t – 3)(t – 1) = 0
4 3 t = 1, 3
35. V = πr a(1) = –6, a(3) = 6
3
dV
= 4πr 2 c. 6t – 12 > 0
dr t > 2; (2, ∞)
dV
When r = 5, = 4π(5) 2 = 100π ≈ 314 m3 per
dr 40. a. Dx ( x19 + x12 + x5 + 100) = 0
20
meter of increase in the radius.
b. Dx ( x 20 + x19 + x18 ) = 20!
20
4 dV
36. V = πr 3 ; = 10
3 dt
c. Dx (7 x 21 + 3 x 20 ) = (7 ⋅ 21!) x + (3 ⋅ 20!)
20
dV dr
= 4πr 2
dt dt
d. Dx (sin x + cos x) = Dx (sin x + cos x)
20 4
dr
When r = 5, 10 = 4π(5) 2
= sin x + cos x
dt
dr 1
= ≈ 0.0318 m/h e. Dx (sin 2 x) = 220 sin 2 x
20
dt 10π
= 1,048,576 sin 2x
1 6 b 3h
37. V = bh(12); = ; b = 20
20 ⎛ 1 ⎞ (–1) (20!) 20!
2 4 h 2 f. Dx ⎜ ⎟ = =
⎝ x⎠ x 21
x 21
⎛ 3h ⎞ dV
V = 6 ⎜ ⎟ h = 9h 2 ; =9
⎝ 2 ⎠ dt dy
dV dh 41. a. 2( x –1) + 2 y =0
= 18h dx
dt dt dy –( x – 1) 1 – x
dh = =
When h = 3, 9 = 18(3) dx y y
dt
dh 1 dy dy
= ≈ 0.167 ft/min b. x(2 y ) + y 2 + y (2 x) + x 2 =0
dt 6 dx dx
dy
38. a. v = 128 – 32t (2 xy + x 2 ) = –( y 2 + 2 xy )
v = 0, when t = 4s dx
dy y 2 + 2 xy
s = 128(4) – 16(4) 2 = 256 ft =−
dx x 2 + 2 xy


3x 2 + 3 y 2
dy dy
= x3 (3 y 2 ) + 3 x 2 y 3 (1)2 + 4(–2)(1) + 8(1)
c. a. dy = – (–0.01)
dx dx 2(–2)(1) + 2(–2 + 2)2
dy
(3 y 2 – 3 x3 y 2 ) = 3x 2 y3 – 3x 2 = –0.0025
dx
(–1)2 + 4(–2)(–1) + 8(–1)
dy 3x 2 y 3 – 3x 2 x 2 y 3 – x 2 b. dy = – (–0.01)
= = 2(–2)(–1) + 2(–2 + 2) 2
dx 3 y 2 – 3 x3 y 2 y 2 – x3 y 2
= 0.0025
⎡ dy ⎤
d. x cos( xy ) ⎢ x + y ⎥ + sin( xy ) = 2 x d 2
⎣ dx ⎦ 45. a. [ f ( x) + g 3 ( x)]
dx
dy
x 2 cos( xy ) = 2 x – sin( xy ) – xy cos( xy ) = 2 f ( x) f ′( x) + 3g 2 ( x) g ′( x)
dx
dy 2 x – sin( xy ) – xy cos( xy ) 2 f (2) f ′(2) + 3g 2 (2) g ′(2)
=
dx x 2 cos( xy ) = 2(3)(4) + 3(2) 2 (5) = 84

⎛ dy ⎞ d
e. x sec 2 ( xy ) ⎜ x + y ⎟ + tan( xy ) = 0 b. [ f ( x) g ( x)] = f ( x) g ′( x) + g ( x) f ′( x)
dx
⎝ dx ⎠
f (2) g ′(2) + g (2) f ′(2) = (3)(5) + (2)(4) = 23
dy
x 2 sec2 ( xy ) = –[tan( xy ) + xy sec2 ( xy )]
dx d
c. [ f ( g ( x))] = f ′( g ( x)) g ′( x)
dy tan( xy ) + xy sec ( xy )
2
dx
=–
dx x 2 sec2 ( xy ) f ′( g (2)) g ′(2) = f ′(2) g ′(2) = (4)(5) = 20

d. Dx [ f 2 ( x)] = 2 f ( x) f ′( x)
′
42. 2 yy1 = 12 x 2
Dx [ f 2 ( x)] = 2[ f ( x) f ′′( x) + f ′( x) f ′( x)]
2
6x 2
′
y1 =
y = 2 f (2) f ′′(2) + 2[ f ′(2)]2
′
At (1, 2): y1 = 3 = 2(3)(–1) + 2(4)2 = 26
′
4 x + 6 yy2 = 0
dx
2x 46. (13) 2 = x 2 + y 2 ; =2
′
y2 = – dt
3y
dx dy
1 0 = 2x + 2 y
′
At (1, 2): y2 = – dt dt
3 dy x dx
′ ′
Since ( y1 )( y2 ) = –1 at (1, 2), the tangents are =–
dt y dt
perpendicular.
When y= 5, x = 12, so
43. dy = [π cos(π x) + 2 x]dx ; x = 2, dx = 0.01 dy 12 24
= – (2) = – = –4.8 ft/s
dt 5 5
dy = [π cos(2π ) + 2(2)](0.01) = (4 + π )(0.01)
≈ 0.0714 y dx
47. sin15° = , = 400
x dt
dy dy y = x sin15°
44. x(2 y ) + y 2 + 2 y[2( x + 2)] + ( x + 2)2 (2) =0
dx dx
dy dx
dy = sin15°
[2 xy + 2( x + 2) 2 ] = –[ y 2 + 2 y (2 x + 4)] dt dt
dx
dy
dy –( y 2 + 4 xy + 8 y ) = 400sin15° ≈ 104 mi/hr
= dt
dx 2 xy + 2( x + 2) 2
2
x 2( x ) 2x2
y 2 + 4 xy + 8 y 48. a.
2
Dx ( x ) = 2 x ⋅ = = = 2x
dy = – dx x x x
2 xy + 2( x + 2)2
x⎛ x ⎞ − x
When x = –2, y = ±1 x
⎛ x⎞ ⎜ ⎟ x−x
b. Dx x = Dx ⎜ ⎟ = ⎝ ⎠
2
= =0
2
⎝ x⎠ x x2


c. Dx x = Dx ( Dx x ) = Dx (0) = 0
3 2 3. x ( x − 1)( x − 2 ) ≤ 0
x ( x − 1)( x − 2 ) = 0
2
d. 2
Dx ( x ) = Dx (2 x) = 2 x = 0, x = 1 or x = 2
The split points are 0, 1, and 2. The expression
sin θ on the left can only change signs at the split
49. a. Dθ sin θ = cos θ = cot θ sin θ points. Check a point in the intervals ( −∞, 0 ) ,
sin θ
( 0,1) , (1, 2 ) , and ( 2, ∞ ) . The solution set is
cos θ
b. Dθ cos θ = (− sin θ ) = − tan θ cosθ { x | x ≤ 0 or 1 ≤ x ≤ 2} , or ( −∞, 0] ∪ [1, 2] .
cos θ

−5 −4 −3 −2 −1 0 1 2 3 4 5
( x + 1)−1/ 2 ; a = 3
1
50. a. f ( x) = x + 1; f '( x) = −
2
4. x3 + 3x 2 + 2 x ≥ 0
L( x) = f (3) + f '(3)( x − 3)
1 (
x x 2 + 3x + 2 ≥ 0 )
= 4 + − (4) −1/ 2 ( x − 3)
2 x ( x + 1)( x + 2 ) ≥ 0
1 3
= 2− x+ = − x+
1 11 x ( x + 1)( x + 2 ) = 0
4 4 4 4
x = 0, x = −1, x = −2
b. f ( x) = x cos x; f '( x) = − x sin x + cos x; a = 1 The split points are 0, −1 , and −2 . The
expression on the left can only change signs at
L( x) = f (1) + f '(1)( x − 1) the split points. Check a point in the intervals
= cos1 + (− sin1 + cos1)( x − 1) ( −∞, −2 ) , ( −2, −1) , ( −1, 0 ) , and ( 0, ∞ ) . The
= cos1 − (sin1) x + sin1 + (cos1) x − cos1 solution set is { x | −2 ≤ x ≤ −1 or x ≥ 0} , or
= (cos1 − sin1) x + sin1
[ −2, −1] ∪ [0, ∞ ) .
≈ −0.3012 x + 0.8415

−5 −4 −3 −2 −1 0 1 2 3 4 5
Review and Preview Problems
x ( x − 2)
5. ≥0
1. ( x − 2 )( x − 3) < 0 x2 − 4
( x − 2 )( x − 3) = 0 x ( x − 2)
≥0
x = 2 or x = 3 ( x − 2 )( x + 2 )
The split points are 2 and 3. The expression on The expression on the left is equal to 0 or
the left can only change signs at the split points. undefined at x = 0 , x = 2 , and x = −2 . These
Check a point in the intervals ( −∞, 2 ) , ( 2,3) , are the split points. The expression on the left can
only change signs at the split points. Check a
and ( 3, ∞ ) . The solution set is { x | 2 < x < 3} or
point in the intervals: ( −∞, −2 ) , ( −2, 0 ) , ( 0, 2 ) ,
( 2,3) .
and ( 2, ∞ ) . The solution set is
−2 −1 0 1 2 3 4 5 6 7 8 { x | x < −2 or 0 ≤ x < 2 or x > 2} , or
( −∞, −2 ) ∪ [0, 2 ) ∪ ( 2, ∞ ) .
2. x2 − x − 6 > 0
( x − 3)( x + 2 ) > 0 −5 −4 −3 −2 −1 0 1 2 3 4 5
( x − 3)( x + 2 ) = 0
x = 3 or x = −2
The split points are 3 and −2 . The expression on
the left can only change signs at the split points.
Check a point in the intervals ( −∞, −2 ) , ( −2,3) ,
and ( 3, ∞ ) . The solution set is
{ x | x < −2 or x > 3} , or ( −∞, −2 ) ∪ ( 3, ∞ ) .

−5 −4 −3 −2 −1 0 1 2 3 4 5

Instructor’s Resource Manual Review and Preview 151

x2 − 9 15. The tangent line is horizontal when the derivative
6. >0 is 0.
x2 + 2
y ' = 2 tan x ⋅ sec 2 x
( x − 3)( x + 3)
>0 2 tan x sec x = 0
x2 + 2
The expression on the left is equal to 0 at x = 3 , 2sin x
=0
and x = −3 . These are the split points. The cos 2 x
expression on the left can only change signs at The tangent line is horizontal whenever
the split points. Check a point in the intervals: sin x = 0 . That is, for x = kπ where k is an
( −∞, −3) , ( −3, 3) , and ( 3, ∞ ) . The solution set integer.
is { x | x < −3 or x > 3} , or ( −∞, −3) ∪ ( 3, ∞ ) . 16. The tangent line is horizontal when the derivative
is 0.
−5 −4 −3 −2 −1 0 1 2 3 4 5 y ' = 1 + cos x
The tangent line is horizontal whenever
f ' ( x ) = 4 ( 2 x + 1) ( 2 ) = 8 ( 2 x + 1) cos x = −1 . That is, for x = ( 2k + 1) π where k is
3 3
7.
an integer.
8. f ' ( x ) = cos (π x ) ⋅ π = π cos (π x )
17. The line y = 2 + x has slope 1, so any line parallel
9. ( )
f ' ( x ) = x 2 − 1 ⋅ − sin ( 2 x ) ⋅ 2 + cos ( 2 x ) ⋅ ( 2 x )
to this line will also have a slope of 1.
For the tangent line to y = x + sin x to be parallel
( )
= −2 x 2 − 1 sin ( 2 x ) + 2 x cos ( 2 x ) to the given line, we need its derivative to equal 1.
y ' = 1 + cos x = 1
x ⋅ sec x tan x − sec x ⋅1 cos x = 0
10. f '( x) = The tangent line will be parallel to y = 2 + x
x2
sec x ( x tan x − 1) π
= whenever x = ( 2k + 1) .
x2 2

18. Length: 24 − 2x
11. f ' ( x ) = 2 ( tan 3 x ) ⋅ sec 2 3 x ⋅ 3
Width: 9 − 2x
( )
= 6 sec 2 3 x ( tan 3 x ) Height: x
Volume: l ⋅ w ⋅ h = ( 24 − 2 x )( 9 − 2 x ) x
= x ( 9 − 2 x )( 24 − 2 x )
( )
1 −1/ 2
12. f '( x) = 1 + sin 2 x ( 2sin x )( cos x )
2
sin x cos x 19. Consider the diagram:
=
1 + sin 2 x 1

13. f ' ( x ) = cos ( x )⋅ 1 x
2
−1/ 2
=
cos x
2 x
x

(note: you cannot cancel the x here because it
is not a factor of both the numerator and 4− x
denominator. It is the argument for the cosine in
the numerator.)
His distance swimming will be
1 −1/ 2 cos 2 x 12 + x 2 = x 2 + 1 kilometers. His distance
14. f ' ( x ) = ( sin 2 x ) ⋅ cos 2 x ⋅ 2 =
2 sin 2 x running will be 4 − x kilometers.
Using the distance traveled formula, d = r ⋅ t , we
d
solve for t to get t = . Andy can swim at 4
r
kilometers per hour and run 10 kilometers per
hour. Therefore, the time to get from A to D will
x2 + 1 4 − x
be + hours.
4 10

152 Review and Preview Instructor’s Resource Manual

20. a. f ( 0 ) = 0 − cos ( 0 ) = 0 − 1 = −1
f (π ) = π − cos (π ) = π − ( −1) = π + 1
Since x − cos x is continuous, f ( 0 ) < 0 ,
and f (π ) > 0 , there is at least one point c
.in the interval ( 0, π ) where f ( c ) = 0 .
(Intermediate Value Theorem)

⎛π ⎞ π ⎛π ⎞ π
b. f ⎜ ⎟ = − cos ⎜ ⎟ =
⎝2⎠ 2 ⎝2⎠ 2
f ' ( x ) = 1 + sin x
⎛π ⎞ ⎛π ⎞
f ' ⎜ ⎟ = 1 + sin ⎜ ⎟ = 1 + 1 = 2
⎝2⎠ ⎝2⎠
The slope of the tangent line is m = 2 at the
⎛π π ⎞
point ⎜ , ⎟ . Therefore,
⎝2 2⎠
π ⎛ π⎞ π
y− = 2 ⎜ x − ⎟ or y = 2 x − .
2 ⎝ 2⎠ 2

π
c. 2x − = 0.
2
π
2x =
2
π
x=
4
The tangent line will intersect the x-axis at
π
x= .
4

21. a. The derivative of x 2 is 2x and the
derivative of a constant is 0. Therefore, one
possible function is f ( x ) = x 2 + 3 .

b. The derivative of − cos x is sin x and the
derivative of a constant is 0. Therefore, one
possible function is f ( x ) = − ( cos x ) + 8 .

c. The derivative of x3 is 3x 2 , so the
1
derivative of x3 is x 2 . The derivative of
3
1
x 2 is 2x , so the derivative of x 2 is x .
2
The derivative of x is 1, and the derivative of
a constant is 0. Therefore, one possible
1 1
function is x3 + x 2 + x + 2 .
3 2

22. Yes. Adding 1 only changes the constant term in
the function and the derivative of a constant is 0.
Therefore, we would get the same derivative
regardless of the value of the constant.

Instructor’s Resource Manual Review and Preview 153

solucionario de purcell 2

More Related Content

What's hot

Similar to solucionario de purcell 2

More from José Encalada

solucionario de purcell 2